�ݺ�ߣ

TABEL
MORTALITAS

9/4/2012

MK. Aktuaria | Darmanto, S.Si.

1

OVERVIEW
• Perusahaan asuransi jiwa mendasarkan semua
perhitungan premi, jumlah asuransi dsb pada
tabel mortalitas/kematian (mortality table).
• Tabel mortalitas berisi peluang seseorang mati
berdasarkan umurnya dari kelompok orang
yang diasuransikan (pemegang polis).

9/4/2012


2

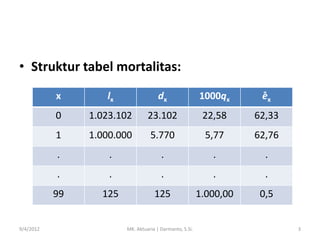
• Struktur tabel mortalitas:
x

dx

1000qx

e̊x

0

1.023.102

23.102

22,58

62,33

1

1.000.000

5.770

5,77

62,76

.

.

.

.

.

.

.

.

.

.

99

9/4/2012

lx

125

125

1.000,00

0,5


3

• lx : jumlah orang yang tepat berusia x.
• Orang yang lahir di saat yg bersamaan disebut
KOHORT, dilambangkan dg l0, dan tersisa
sebanyak lx orang yg mencapai usia x
• dx : jumlah orang yg mati sebelum mencapai
usia x+1 tahun. Jadi,
lx+1 = lx – dx
9/4/2012


4

• Misal, w : usia tertinggi --->> lw > 0 dan lw+1 = 0.
Artinya, w adalah usia tertinggi yg dapat dicapai
oleh suatu kohort.

• 1000qx : peluang seseorang berusia x akan
meninggal sebelum usia x+1 dikalikan 1000 (agar
tidak terlalu banyak angka di belakang koma)
• e̊x : harapan hidup seseorang pada usia x
9/4/2012


5

• Tabel mortalitas yg umum digunakan adalah
Commisioners Standard Ordinary (CSO) 1941
Mortality Table yang berasal dari AS.
• Cara membuat tabel mortalitas ialah mengamati
sejumlah kohort, kemudian mencatat berapa banyak
orang tsb yang mati setiap tahun sampai kohort yg
diamati mati semuanya.
• Apa kesulitannya…??? --->> Yang mengamati mati
dulu sebelum semua anggota kelompok yg diamati
mati semuanya.
9/4/2012


6

TABEL MORTALITAS CSO 1941
(COMMISIONERS STANDARD ORDINARY)

9/4/2012


7

• Dari tabel dapat dilihat bahwa:
l0 = 1.023.102 orang ;
l9 = 973.869 orang;
w = 99 tahun ;
d23 = 2.531 orang;
q13 = 1,98/1000 = 0,00198;
e̊34 = 34,29 tahun.
9/4/2012


8

• Sejumlah l0 yg dipilih sembarang disebut radix.
• Perhatikan:

lx  lx 1 d x
qx 

lx
lx

Artinya: peluang seseorang yg berusia x akan mati
sebelum hari ulang tahunnya yg ke x+1 sama dengan
banyaknya orang dlm kohort yg mati antara usia x dan
x+1 (dx) dibagi dgn jumlah orang yang berusia x (lx).
9/4/2012


9

• npx ialah peluang seseorang berusia x akan hidup
(paling sedikit) n tahun.
n

lx  n
px 
lx

Atau, npx adalah jumlah orang (dari sebanyak lx pada
usia x) yg mencapai usia x+n (lx+n) dibagi jumlah
orang pada usia x.

lx 1
Bila n=1, penulisannya: 1px=px. Jadi, px 
lx
9/4/2012


10

• nqx menyatakan peluang seseorang berusia x
akan meninggal dalam n tahun, atau sebelum
mencapai n+x tahun.
n

qx  1  n

lx  n
px  1 
lx
lx  lx  n

lx

• Bila n=1, ditulis: 1qx = qx = 1 – px.
9/4/2012


11

•

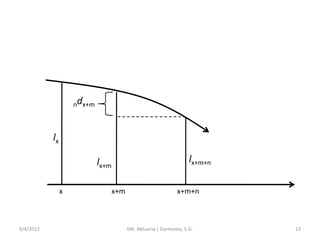
m|nqx

ialah peluang seseorang yang berusia x
akan hidup m tahun tetapi mati dalam n
tahun kemudian, yaitu mati antara usia x+m
dan x+m+n tahun.
lx  m  lx  m  n n d x  m

m|n qx 
lx
lx

d xm
• Bila n=1, ditulis: m|1qx = m|qx. Jadi, m| qx 
lx
9/4/2012


12

ndx+m

lx

lx+m
x

9/4/2012

x+m

lx+m+n
x+m+n


13

CONTOH
1) Dengan menggunakan tabel CSO 1941,
berapakah peluang seseorang berusia 40 thn
akan mati antara usia 55 dan 60 thn?

Jawab:
• x = 40 ; x+m = 55 -->> m = 15 ; x+m+n = 60 ->> n = 5
•
9/4/2012

m|nqx

= 15|5q40

14

•

15|5q40 =

(l55 – l60)/(l40)
= (754.191 – 677.771)/(883.342)
= 0,08651

• Jadi peluang orang yg berusia 40 thn itu mati
antara usia 55 dan 60 thn adalah 0,08651.
• Atau 15|5q40 = 15p40 . 5q55
9/4/2012


15

2) Suatu keluarga mempunyai 2 anak, masing2
berusia 1 thn dan 11 thn. Carilah peluang tepat
seorang anak akan mati sebelum usia 50 thn?

Jawab:
Ada dua kejadian yakni anak 1 thn mati tapi 11 thn
hidup atau anak 1 thn hidup tapi 11 thn mati. Tiap
kejadian bersifat independent sedangkan dua
kejadian bersifat mutually exclusive.
9/4/2012


16

Shg, Peluang tepat seorang anak akan mati
sebelum usia 50 thn adalah
= 49q1 . 39p11 + 49p1 . 39q11
= (l1 – l50)/(l1) . (l50)/(l11) + (l50)/(l1) . (l11 – l50)/(l11)
= l50.(l1 + l11 -2l50) / (l1 . l11)
= 810.900 (1.000.000 + 969.890 – 2(810.900)) /
[(1.000.000)(969.890)
= 0,29103
9/4/2012


17

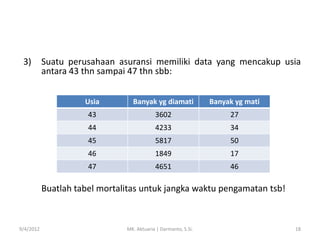
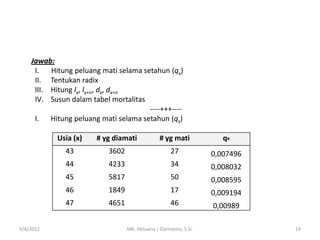
3)

Suatu perusahaan asuransi memiliki data yang mencakup usia
antara 43 thn sampai 47 thn sbb:
Usia

Banyak yg diamati

Banyak yg mati

43

3602

27

44

4233

34

45

5817

50

46

1849

17

47

4651

46

Buatlah tabel mortalitas untuk jangka waktu pengamatan tsb!

9/4/2012


18

Jawab:
I.
Hitung peluang mati selama setahun (qx)
II. Tentukan radix
III. Hitung lx, lx+n, dx, dx+n
IV. Susun dalam tabel mortalitas
----+++---I. Hitung peluang mati selama setahun (qx)
Usia (x)

# yg mati

qx

43

3602

27

0,007496

44

4233

34

0,008032

45

5817

50

0,008595

46

1849

17

0,009194

47
9/4/2012

# yg diamati

4651

46

0,00989


19

II. Misal radix, l43 = 100.000 -->> sembarang
II. d43
l44
d44
l45
dst….

9/4/2012

= (100.000)(0,007496) ≈ 750
= 100.000 – 750 = 99.250
= (99.250)(0,008032) ≈ 797
= 99.250 – 797 = 98.453


20

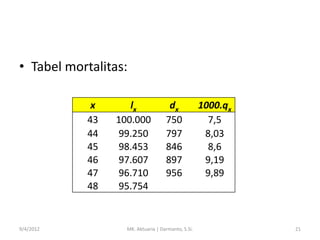
• Tabel mortalitas:
x
43
44
45
46
47
48

9/4/2012

lx
100.000
99.250
98.453
97.607
96.710
95.754

dx
750
797
846
897
956


1000.qx
7,5
8,03
8,6
9,19
9,89

21

HARAPAN HIDUP
• ex menyatakan harapan hidup menurut usia.
• Dua macam harapan hidup:
– ex ,Curtate expectation of life (harapan hidup
ringkas)
– ex ,Complete expectation of life (harapan hidup
lengkap

9/4/2012


22

• Harapan hidup diringkas,
Artinya, rata-rata jumlah tahun yg lengkap yg masih
akan dialami oleh seseorang yg sekarang berusia x
tahun.

• Tahun yang lengkap,
Artinya, tahun yang penuh dialami. Misal, orang
lahir 21 Juli 1987 dan mati 18 Oktober 2011, maka
dianggap dia mati 21 Juli 2011, sdg sisanya tidak
diperhitungkan
9/4/2012


23

• Misal; Pandang sebanyak lx orang yg semua
tepat berusia x tahun. Sebanyak lx+1 orang
darinya masih akan hidup pd tahun ke x+1,
sebanyak lx+2 orang darinya masih akan hidup
pada tahun ke x+2, dst, dan tinggal lw yg masih
hidup untuk tahun terakhirnya. Jadi jumlah
tahun lengkap yg dialami oleh lx orang sampai
semua mati adl
lx1  lx 2   lw
9/4/2012


24

• Artinya, setiap orang dari lx pada rata-ratanya
mpy harapan hidup,
lx 1  lx  2 
ex 
lx

9/4/2012


 lw

25

• Contoh: Hitunglah e95 untuk tabel CSO 1941!
• Dari tabel, didapatkan l95 = 3011, l96= 1818, l97
= 1005, l98 =454 dan l99 = 125, jadi
l96  l97  l98  l99
e95 
l95
1818  1005  454  125

3011
 1,13 tahun
9/4/2012


26

• Karena,
lx 1
lx  2
lx 3
 px ;
 2 px ;
 3 px ;
lx
lx
lx

lw
; 
lx

w x

px

maka,
ex  px  2 px  3 px 

9/4/2012

 w x px


27

• Bila dalam perhitungan harapan hidup, tahun
tidak lengkap yang dialami seorang anggota lx
ikut diperhitungkan (complete expectation of
life), maka harapan hidup didefinisikan
sebagai,
1
e 
lx

w x

o
x

l

x t

dt

0

w x





t

px dt

0
9/4/2012


28

• Untuk interval [0,1]
1

l

x t

0

lx  lx 1
dt ≒
2

• Untuk interval [1,2]
2

l
1

9/4/2012

x t

lx 1  lx  2
dt ≒
2


29

• Dengan cara yg sama untuk semua interval
didapatkan,
1  lx  lx 1 lx 1  lx  2
e ≒ 


lx  2
2
o
x





• Didekati dgn,
1
e ≒ ex 
2
o
x

9/4/2012


30

• Contoh: Hitunglah eo95 untuk CSO 1941!
1
e ≒ e95 
2
1
≒ 1,13  ≒ 1, 63
2
o
95

9/4/2012


31

• Contoh: Buktikan ex = px (1 + ex+1)
lx 1  lx  2  lx 3  lx  4 
px 1  ex 1  
1 
lx 
lx 1

 lw 



lx 1  lx 1  lx  2  lx 3  lx  4 


lx 
lx 1

lx 1  lx  2  lx 3  lx  4 

lx

 lw 




 lw

 ex (terbukti).
9/4/2012


32

• Contoh: Buktikan dan jelaskan kebenaran bukti tsb dengan
kalimat verbal bahwa,
qx + px.qx+1 + 2px.qx+2 + …… = 1

Bukti:

qx  px qx 1  2 px qx 1 
d x lx 1 d x 1 lx  2 d x  2
 


lx
lx lx 1
lx lx  2


1
 d x  d x 1  d x  2 
lx



lx
lx

1
9/4/2012


(terbukti).
33

• Kebenaran dalam kalimat verbal:
Suku pertama qx menyatakan peluang seorang yg berusia x
tahun mati sebelum x+1 tahun, artinya mati pada interval
waktu (x, x+1). Suku kedua px.qx+1 menyatakan peluang
orang tsb mencapai usia x+1 tahun dan mati sebelum x+2
tahun, atau mati pada interval waktu (x+1, x+2). Suku ketiga
2px.qx+2 menyatakan peluang orang tsb mencapai x+2 tahun
dan mati sebelum x+3 tahun, atau mati pada interval waktu
(x+2, x+3), dan demikian seterusnya, sehingga jika
dijumlahkan semua maka sesungguhnya jumlah tersebut
adalah peluang seorang mati pada tahun-tahun berikutnya.
Dikarenakan orang pasti mati, maka jumlah peluang
tersebut harus sama dengan 1.
9/4/2012


34

TABEL MORTALITAS PRIA AMERIKA
• Tabel CSO 1941 hanya ditentukan oleh usia x tahun saja.
• Realitas: asurador tidak memberikan polis pada mereka yg
sekarat atau faktor lain yg dianggap merugikan perusahaan.

• Misal, difokuskan masalah kesehatan, asurador terkadang
mensyaratkan adanya tes kesehatan. Polis diberikan jika
calon tidak mengidap penyakit yg “dianggap” berbahaya.
Sehingga, tingkat kesehatan orang yg baru diasuransikan
rata-rata lebih baik drpd yg sudah agak lama diasuransikan,
pada umur yg sama. Akibatnya, diasumsikan peluang mati
orang yg baru diasuransikan lebih rendah drpd orang yg
sudah agak lama diasuransikan.
9/4/2012


35

• Kondisi semacam itu, disebut pengaruh seleksi permulaan.
• Pengaruh seleksi permulaan akan hilang beberapa tahun kemudian,
artinya peluang mati mereka sama dg orang lain pada usia x,
sehingga pada kondisi ini peluang mati hanya tergantung pada usia
x tahun saja.
• Tabel mortalitas yg memperhitungkan pengaruh seleksi permulaan
disebut select, sedangkan yg tidak memperhitungkan pengaruh
seleksi/yg pengaruhnya telah hilang disebut ultimate.
• Biasanya, pengaruh seleksi permulaan dianggap hilang setelah 3 – 5
tahun.

9/4/2012


36

Year of Insurance

Age at
Issue (x)

1

2

3

4

5

15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

2.47
2.52
2.56
2.61
2.66
2.73
2.78
2.83
2.86
2.91
2.93
2.95
2.98
2.98
2.99

3.24
3.31
3.37
3.44
3.52
3.59
3.66
3.72
3.76
3.8
3.84
3.86
3.88
3.91
3.92

3.41
3.48
3.55
3.64
3.72
3.8
3.86
3.91
3.96
3.99
4.02
4.04
4.06
4.06
4.08

3.55
3.63
3.73
3.81
3.89
3.96
4.01
4.06
4.08
4.11
4.12
4.13
4.14
4.14
4.17

3.72
3.82
3.92
4
4.07
4.13
4.18
4.21
4.24
4.26
4.27
4.28
4.29
4.32
4.37

9/4/2012


6 and
over
3.92
4.02
4.12
4.18
4.25
4.31
4.35
4.39
4.41
4.43
4.46
4.48
4.51
4.59
4.68

Attained
Age
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
37

• Perhatikan:
Angka 3,72 untuk usia dikeluarkan (age of
issue) 19 tahun dan lama diasuransikan (year
of insurance) 3 tahun, menyatakan bahwa
peluang seseorang yg sekarang berusia 21
tahun yg diasuransikan pada usia 19 tahun
akan mati sebelum usia 22 tahun adl
3, 72
 0, 00372
1000
9/4/2012


38

• Perhatikan:
• Bilangan 4,43 untuk capaian usia (attained age)
29 tahun pada lama asuransi 6 dan lebih (6 and
over) menyatakan bahwa peluang seseorang yg
sekarang berusia 29 tahun dan yg telah
diasuransikan paling sedikit 5 tahun yg lalu akan
mati sebelum mencapai usia 30 tahun adalah
0,00443.
• Kolom “6 and over” adl ultimate.
9/4/2012


39

• Contoh:
• Gunakan tabel mortalitas pria amerika untuk
menghitung peluang berikut:
a) Berapakah peluang seorang pria yg sekarang
berusia 19 tahun yg diasuransikan 2 tahun lalu
akan mati antara usia 20 – 21 thn?
b) Akan hidup mencapai usia 21 tahun?
c) Akan mati antara usia 24 – 25 tahun?
9/4/2012


40

a)

Agar org itu dapat mati antara usia 20 thn dan 21 thn, maka dia
harus mencapai usia 20 thn dan mati setahun kemudian. Usia org
itu diasuransikan adl 17 thn. Peluang mencapai usia 20 thn = 1 –
0,00355 dan peluang mati ketika usia 21 thn adl 0,00373.
Sehingga, peluang mati antara usia 20 – 21 thn adl
= (1-0,00355) (0,00373) = 0,00372

b)

Peluang mencapai usia 21 thn adl
= (1-0,00355) (1-0,00373) = 0,99273

c)

Peluang mati antara usia 24 – 25 thn adl
= (1-0,00355)(1-0,00373)(1-0,00392)(1-0,00412)(10,00418)(0,00425)
= 0,00417

9/4/2012


41

LATIHAN
1. Dua orang masing-masing berusia 18 dan 23
tahun. Berapakah peluangnya,
a) Paling sedikit seorang mencapai usia 60 thn?
b) Keduanya mati sebelum mencapai usia 40 thn?

2. Berapakah peluangnya seorang yg sekarang
berusia 27 tahun akan mati antara usia 62
dan 68 tahun?
9/4/2012


42

3. Peluang seseorang berusia 18 akan mencapai usia 28
tahun adl 0,95 dan peluang orang tsb mencapai usia
48 thn adl 0,75. Carilah peluang seseorang berusia 28
thn akan mati sebelum mencapai usia 48 thn!
4. Hitung peluang:
a) Seseorang yg sekarang berusia 21 thn yg diasuransikan 3
tahun lalu akan mati antara usia 22 dan 23!
b) Akan mencapai 24 tahun!
c) Akan mati antara usia 25 dan 26!

9/4/2012


43

5. Buktikan bahwa:
a)
b)

9/4/2012

m|nqx

= mpx . nqx+m
m+npx = mpx – m|nqx


44

�ݺ�ߣ

Akt 2-tabel-mortalitas

More Related Content

Akt 2-tabel-mortalitas