FUNCIONES CIRCULARES.pptx
- 1. 6.53 Circular and Periodic Functions Lesson 11.3 Prof. Juan Serrano, MEd.
- 2. Circular and Periodic Functions 2 Explore Trigonometric Functions of Special Angles Todayâs Goals ï§ Find value of trigonometric functions given a point on a unit circle or the measure of a special angle. ï§ Find values of trigonometric functions that model periodic events. Todayâs Vocabulary ï§ Unit circle ï§ Circular functions ï§ Periodic functions ï§ Cycle ï§ Period
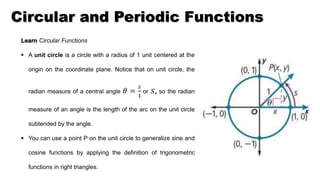
- 3. Circular and Periodic Functions Learn Circular Functions ï§ A unit circle is a circle with a radius of 1 unit centered at the origin on the coordinate plane. Notice that on unit circle, the radian measure of a central angle ð = ð 1 or ð , so the radian measure of an angle is the length of the arc on the unit circle subtended by the angle. ï§ You can use a point P on the unit circle to generalize sine and cosine functions by applying the definition of trigonometric functions in right triangles.
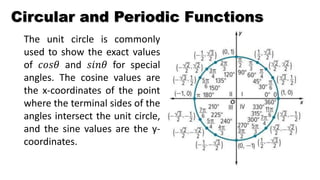
- 5. The unit circle is commonly used to show the exact values of ððð ð and ð ððð for special angles. The cosine values are the x-coordinates of the point where the terminal sides of the angles intersect the unit circle, and the sine values are the y- coordinates. Circular and Periodic Functions
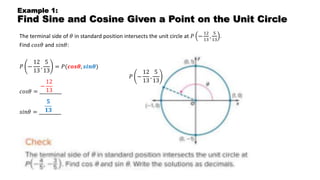
- 6. Example 1: Find Sine and Cosine Given a Point on the Unit Circle The terminal side of ð in standard position intersects the unit circle at ð â 12 13 , 5 13 . Find ððð ð and ð ððð: ð â 12 13 , 5 13 = ð(ðððð―, ðððð―) ððð ð = __________ ð ððð = __________ â 12 13 ð ðð ð â 12 13 , 5 13
- 7. Example 1: Find Trigonometric Values of Special Angles Find exact values of the six trigonometric functions for an angle that measure 5ð 4 radians: Using the unit circle, we know that special angle 5ð 4 intersect the unit circle in Quadrant III at P â 2 2 , â 2 2 . ððð ð = _________ ð ððð = _________ â ð ð â ð ð