Incremental
- 1. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey Dimitri P. Bertsekas Optimization for Machine Learning 勉強会 中川研M1 山田直敬 12年5月24日木曜日 1
- 2. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 2
- 3. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order TODAY’S TOPIC 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 3
- 4. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 4
- 5. Incremental Method Additive cost Problem ex.) loss func. mがとても大きい場合、すべての?(x) を計算してから勾配を求めるの は高コスト その代わり? を一つずつ取り、その値を用いて少しずつ更新していく 全部足して計算するよりも性能が良くなる可能性がある。 12年5月24日木曜日 5
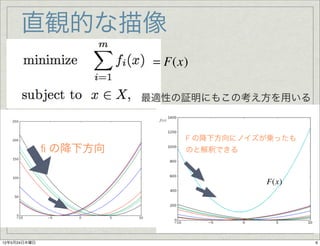
- 6. 直観的な描像 = F(x) 最適性の証明にもこの考え方を用いる f (x) F の降下方向にノイズが乗ったも ? の降下方向 のと解釈できる F(x) 12年5月24日木曜日 6
- 7. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 7
- 8. Example 1.1: Least Squares and Inference f_i(x) = 二乗誤差 (a_i,b_i): given. 特徴ベクトルとラベルの組 xbar : given 12年5月24日木曜日 8
- 9. Example 1.1: Least Squares and Inference L1正則化 ニューラルネットワーク 最尤推定、EM 12年5月24日木曜日 9
- 10. Example 1.2: Dual Optimization in Separable Problems DUAL m 導出は同著NONLINEAR本 5.1.6節より 凸関数 12年5月24日木曜日 10
- 11. Example 4.3: Minimization of an Expected Value - Stochastic Programming m = ∑ π i H (x,wi ) i=1 Hはxと確率変数w の関数 ただし、wはm通りの可能な値がある(m>>1) P(w = wi ) = π i i = 1,..., m このときHの期待値を最小化するようなxを求める 12年5月24日木曜日 11
- 12. Example 4.3: Minimization of an Expected Value - Stochastic Programming あるいは wi を独立なサン プルだと思うと、 は E{H (x,w)}の近似である これもADDITIVE COST PROBLEMの一つ 12年5月24日木曜日 12
- 13. Example 4.4: Problems with Many Constraints 制約の数が大きい場合、ペナルティ 関数を用いることで無制約化する 例 十分大きなcを設定 するのがポイント 12年5月24日木曜日 13
- 14. Example 4.4: Problems with Many Constraints { x ∈? i=1 Xi m closed set 十分大きなγを設定 12年5月24日木曜日 14
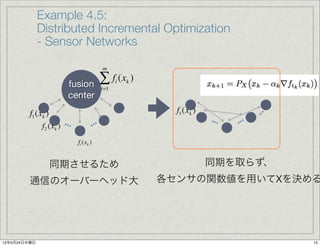
- 15. Example 4.5: Distributed Incremental Optimization - Sensor Networks m fusion ∑ f (x ) i k i=1 center f1 (xk ) f1 (xk ) f2 (xk ) ... ... ... ... fi (xk ) 同期させるため 同期を取らず、 通信のオーバーヘッド大 各センサの関数値を用いてXを決める 12年5月24日木曜日 15
- 16. Example 4.6: Weber Problem in Loation Theory x (weighted) 1- meansとも解釈できる 12年5月24日木曜日 16
- 17. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 17
- 18. Incremental Gradient Methods に対して、 f_iが微分可能とする(凸性は必要なし) 歴史は長い。”back propagation” もこの形 ikの選び方は周期的に取るか、乱択によって決める ik = (k mod m) + 1 まんべんなく?f_ikを評価するために、反復数はm回以上取る 12年5月24日木曜日 18
- 19. incremental vs. nonincremental (a)反復しはじめ (b) 収束に近いとき incrementalは精細さに incrementalは収束困難 は欠くが、とにかく進 α_kを減少させて強制 んでみる 的に収束させる nonincrementalよりも 収束率がsublinearで遅 格段に早く前進 α_k=定数だと振動 12年5月24日木曜日 19
- 20. Incremental Gradient の収束メカニズム ik = (k mod m) + 1 , α k は同周期では一定として、1周期反復させる。 incremental gradient の1周期は ふつうのnonincremental gradient 1反復に対応する。つまり、 ノイズとして解釈 ここで、 である。?f がLipschitz連続であることを用いると、 ek = O(α k ) α が言える。 k = O(1 / k) のようにstepsizeを減衰させると誤差の収束も保証 12年5月24日木曜日 20
- 21. remark: incremental gradient method ≒ stochastic gradient descent SGD m = ∑ π i H (x,wi ) i=1 に対して ( wk は w のサンプル点) incremental methodも, ikが確率1/mで一様にサンプルされ ていると解釈すればSGDとみなせる 12年5月24日木曜日 21
- 22. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 22
- 23. Incremental subgradient Methods f が微分不可能だが、convexである場合 ~ ? f (x) ∈? f (x) 収束させるには step sizeを減少させる必要あり 収束レートはsublinear (遅い) but, subgradientの場合、nonincremental 版でも収束率が sublinearなので、incrementalを使ったほうがお徳 12年5月24日木曜日 23
- 24. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 24
- 25. Incremental proximal methods proximal minimization algorithm [Rochafellar 76] ? 1 2? xk+1 = arg min ? f (x) + x ? xk ? x∈X ? 2α k ? これのincremental版 12年5月24日木曜日 25
- 26. Incremental proximal methods 嬉しいこと cost関数 f によってはarg min が closed formで 求められる( ex. f(x) = ||x - c||^2 ) その場合は安定なiterationの列{x_k} が得られる cf.) (sub)gradientの場合はstep sizeによっては 関数値が小さくならないことが起きてしまう 12年5月24日木曜日 26
- 27. Incremental proximal methods しかし、 arg min が closed formで求められる関数 f は限られ ている。 求められない場合、各反復ごとに最適化問題を解く ことになるので不便 12年5月24日木曜日 27
- 28. Incremental proximal methods しかし、 arg min が closed formで求められる関数 f は限られ ている。 求められない場合、各反復ごとに最適化問題を解く ことになるので不便 proximalで解けるものはproximalで解く そうでないものは(sub)gradientで更新 12年5月24日木曜日 28
- 29. cost function decomposition proximalで解けるものはproximalで解く そうでないものは(sub)gradientで更新 proximalで解きやすい形 その他はsubgradient 12年5月24日木曜日 29
- 30. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 30
- 31. Incremental subgradient proximal methods に対して 2段階の最適化を行う このスキームで、元の最適化問題の十分な近似解が得られるこ と、及びk ->∞では最適解が一致することの証明は来週?[予定] 12年5月24日木曜日 31
- 32. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 32
- 33. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 33
- 34. 4.5.1 Regularized Least Square 例えばL1正則化だと、 ここで γ 1 ' fi (x) = x 1 ,hi (x) = (ci x ? di ) とおけば 2 m 2 (SUB)GRADIENT DESCENT CLOSED FORM 12年5月24日木曜日 34
- 35. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 35
- 36. 4.5.2 Iterated Projection Algorithm feasibility problem ≈ PROXIMAL f (x) SUBGRADIENT 12年5月24日木曜日 36
- 37. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order NEXT WEEK’S TOPIC 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 37
- 38. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods お話 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order TODAY’S TOPIC 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 38
- 39. 结构ややこしいので、先にふつうの gradient methodにおける一般論を話します 目的関数は F(x) = ∑ f(x) として考えます 簡単のため x ∈ R^n で考えます 定数ステップサイズ、減衰ステップサイズに対してはFの Lipshitz連続性を仮定すれば最適解に収束することを紹介 勾配に誤差が乗った場合の収束性を紹介 incremental methodが、誤差ありの勾配法と見做せるこ とから、上記の一般論を利用して証明を行う 12年5月24日木曜日 39
- 40. gradient methodが定数ステップサイズ で収束する条件(Nonlinear本 prop.1.2.3) {x_k}をgradient method で得られた系列とする。 i.e. x k+1 = x k + α k d k ,where?F(x k )'d k < 0 F(x)がLipshitz連続 ?L > 0,?x, y ∈? , ?F(x) ? ?F(y) ≤ L x ? y n 2 k 2 2 ?c1 ,c2 ,c1 ?F(x ) ≤ ??F(x )'d , d k k k ≤ c2 ?F(x ) k このとき gradient descentは次のαで局所最適解 c1 (2 ? ε ) に収束する ε ≤α ≤ L 12年5月24日木曜日 40
- 41. gradient methodが減衰ステップサイズで 収束する条件(Nonlinear本 prop.1.2.4) {x_k}をgradient method で得られた系列とする。 i.e. x k+1 = x + α d ,where?F(x )'d < 0 k k k k k F(x)がLipshitz連続 ?L > 0,?x, y ∈? n , ?F(x) ? ?F(y) ≤ L x ? y 2 k 2 2 ?c1 ,c2 ,c1 ?F(x ) ≤ ??F(x )'d , d k k k ≤ c2 ?F(x ) k ∞ 減衰ステップサイズ α → 0, k ∑α k =∞ k=0 このとき gradient descentは最適値F*に収束する inf F(x) = F * x∈X 12年5月24日木曜日 41
- 42. 驳谤补诲颈别苍迟に误差が乗っている场合の 収束性について gradientが正確に計算できず、エラー付きでしか得られない場合の 更新式は次のようになる。 g = ?F(x ) + e k k k x k+1 = x ?α g k k k ≤ δ ならば、収束先の値は F + O(δ ) * eが有界 すなわち ?k, e k となる。 eがstepsizeに比例する場合、すなわち ek ≤ α k q のとき、 α->0で収束先はF*に一致する 一般論おわり 12年5月24日木曜日 42
- 43. ポイント incremental method一周ぶんを gradientに誤差が乗ったものと解釈して 収束性を評価する (F : Lipshitz) & (||e|| ≦ αq ) 十分小さな定数ステップサイズαを用いると O(α)-最適解に収束する (F : Lipshitz) & (||e^k|| ≦ α^k q ) & (α^k ->0) & ( ∑ α^k = ∞ ) 減衰ステップサイズで更新すればincremental methodを使っても元の最適解に収束する! 12年5月24日木曜日 43
- 44. ここから本题 Incremental subgradient proximal methods の収束性の評価 に対して (sub)gradient methodの収束性は吟味できる(ことに している)が、z_kの更新式はどう評価すればよい か? 12年5月24日木曜日 44
- 45. ここから本题 Incremental subgradient proximal methods の収束性の評価 実は は ? zk = PX (xk ? α k ? f (zk )) と書きなおすことができる。 すなわちproximal methodの更新式は、(sub)gradientのよう な形で表せて、subgradientの収束性の証明を流用できる。 12年5月24日木曜日 45
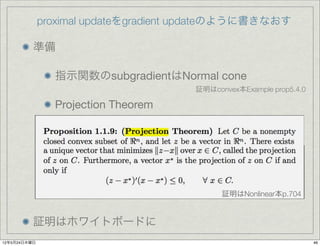
- 46. proximal updateをgradient updateのように書きなおす 準備 指示関数のsubgradientはNormal cone 証明はconvex本Example prop5.4.0 Projection Theorem 証明はNonlinear本p.704 証明はホワイトボードに 12年5月24日木曜日 46
- 47. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 47
- 48. incremental proximal subgradient method の収束性 に対して リプシッツ連続性と 誤差ありの勾配法を思い出す 2段階で更新 12年5月24日木曜日 48
- 49. cyclic orderによる収束性評価 (定数ステップサイズ) m^2 12年5月24日木曜日 49
- 50. cyclic orderによる収束性評価 (定数ステップサイズ) FをF*+O(ε)に収束させるためにはα=O(ε(mc)^-2) くらい 小さくなければならない すると必要な反復数はN=O(m^3 c^2/ ε^2) さすがに多すぎる.... 12年5月24日木曜日 50
- 51. cyclic orderによる収束性評価 (減衰ステップサイズ) αをゆっくり収束させてやれば一応最適解は求められる 12年5月24日木曜日 51
- 52. Chapter 4 Incremental Gradient, Subgradient, and Proximal Methods for Convex Optimization: A Survey 4.1 Introduction 4.1.1 Some Examples of Additive Cost Problems 4.1.2 Incremental Gradient Methods - Differentiable Problems 4.1.3 Incremental Subgradient Methods - Nondifferentiable Problems 4.1.4 Incremental Proximal Methods 4.2 Incremental Subgradient-Proximal Methods 4.3 Convergence for Methods with Cyclic Order 4.4 Convergence for Methods with Randomized Order 4.5 Some Applications 4.5.1 Regularized Least Squares 4.5.2 Iterated Projection Algorithms 12年5月24日木曜日 52
- 53. 収束証明には下记の定理をうまく利用する 本文中ではWk=0の場合で用いられている Zk > 定数 を仮定し、矛盾を導く という使い方がされている 12年5月24日木曜日 53
- 55. ここまでは肠测肠濒颈肠 気持ちだけ... 版と共通 条件付き期待値を取ると martingaleっぽい形が現れる 12年5月24日木曜日 55
- 56. randomized orderによる収束性評価 (定数ステップサイズ) m^1 直観的には、 式(4.4.8)と(4.3.9)を見比べると、random版は期待値で 評価するため1/mがかかっているのが全体に効いている 12年5月24日木曜日 56
- 57. randomized orderによる収束性評価 (定数ステップサイズ) 先の例と同様に考えると、α=O(m^-1 c^-2)でε近似 そのために必要な反復数の期待値は (mc)^2/ε^2以下 一応嬉しいのだが、オーダーと期待値の比較はややナンセンス 12年5月24日木曜日 57
- 58. randomized orderによる収束性評価 (減衰ステップサイズ) 同様のことが成り立つ 12年5月24日木曜日 58
- 59. 参考文献 [Nonlinear本]: D.Bertsekas “Nonlinear Programming” Athena Scienti?c 1999 [convex本]: D.Bertsekas “Convex Optimization Theory” Athena Scienti?c 2009 D.Bertsekas and Tsisiklis “Gradient Convergence in Gradient Methods” 2000 12年5月24日木曜日 59























![Incremental proximal methods
proximal minimization algorithm [Rochafellar 76]
? 1 2?
xk+1 = arg min ? f (x) + x ? xk ?
x∈X
? 2α k ?
これのincremental版
12年5月24日木曜日 25](https://image.slidesharecdn.com/incremental-120606111149-phpapp02/85/Incremental-25-320.jpg)





![Incremental subgradient proximal methods
に対して
2段階の最適化を行う
このスキームで、元の最適化問題の十分な近似解が得られるこ
と、及びk ->∞では最適解が一致することの証明は来週?[予定]
12年5月24日木曜日 31](https://image.slidesharecdn.com/incremental-120606111149-phpapp02/85/Incremental-31-320.jpg)


























![参考文献
[Nonlinear本]: D.Bertsekas “Nonlinear
Programming” Athena Scienti?c 1999
[convex本]: D.Bertsekas “Convex Optimization
Theory” Athena Scienti?c 2009
D.Bertsekas and Tsisiklis “Gradient Convergence
in Gradient Methods” 2000
12年5月24日木曜日 59](https://image.slidesharecdn.com/incremental-120606111149-phpapp02/85/Incremental-59-320.jpg)