Sporadic Model Building for Efficiency Enhancement of hBOA
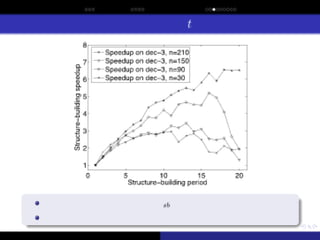
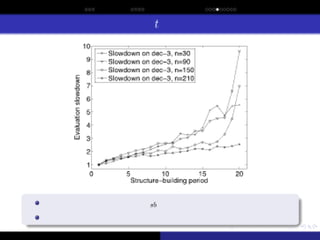
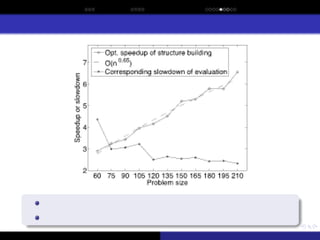
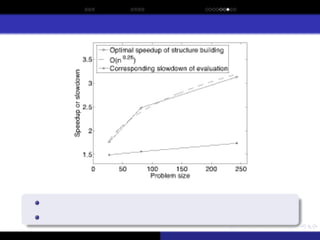
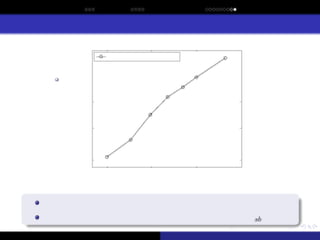
This paper describes and analyzes sporadic model building, which can be used to enhance the efficiency of the hierarchical Bayesian optimization algorithm (hBOA) and other estimation of distribution algorithms (EDAs). With sporadic model building, the structure of the probabilistic model is updated once every few iterations (generations), whereas in the remaining iterations only model parameters (conditional and marginal probabilities) are updated. Since the time complexity of updating model parameters is much lower than the time complexity of learning the model structure, sporadic model building decreases the overall time complexity of model building. The paper shows that for boundedly difficult nearly decomposable and hierarchical optimization problems, sporadic model building leads to a significant model-building speedup that decreases the asymptotic time complexity of model building in hBOA by a factor of ╬ś(n0.26) to ╬ś(n0.65), where n is the problem size. On the other hand, sporadic model building also increases the number of evaluations until convergence; nonetheless, for decomposable problems, the evaluation slowdown is insignificant compared to the gains in the asymptotic complexity of model building.