深层学习の非常に简単な説明
- 2. はじめに:ビギナーの方へ (1/2) ?深層学習の基本を極力平易に説明したつもりです ?ちょっと普通の入門書とは違った角度から攻めてます ? (Back Propagationなどの)「学習法」は説明していません ? (学習後に)「どういう風に動作するものなのか」を中心にしています ? (学習後の)動作がわかった後に,学習原理を学ぶとよいと思います ?前半は,深層学習以前の(30年ぐらいまえの)多層ニュー ラルネットワークの解説です ?それを踏まえたほうが,多層化の意味も分かりやすいんじゃないかと 2
- 5. じゃぁ,はじめましょう! まずは「パターン認識」の基本 パターン認識をよく知っている人は 「ところで,特徴もイロイロある」のスライドへジャンプしてOK 5 計算機に「これは何か」を 答えさせる技術
- 10. この基本原理を座標空間で見ると...(4/8) 色特徴 テクスチャ (模様)特徴 豚肉=(色,形,模様,..., なんちゃら) =(10, 2.5, 4.3,..., 5.9) ※これらの数字はテキトーです 3つ以上の特徴で表されると,その分だけ 座標軸が要りますが,まぁ気にしない なんちゃら 特徴 ※高校だと3数字の組=3次元ベクトルまでしか習わないでしょうね.でもd(>3)個の数字の組にしたってOK. d次元ベクトル.
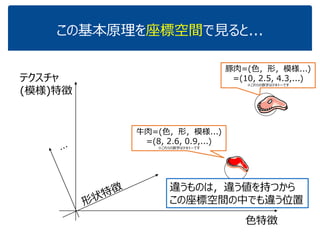
- 11. この基本原理を座標空間で見ると...(5/8) 色特徴 テクスチャ (模様)特徴 牛肉=(色,形,模様,..., なんちゃら) =(8, 2.6, 0.9,..., 7.2) ※これらの数字はテキトーです 違うものは,違う値を持つから この座標空間の中でも違う位置 豚肉=(色,形,模様,..., なんちゃら) =(10, 2.5, 4.3,..., 5.9) ※これらの数字はテキトーです なんちゃら 特徴
- 15. ところで,特徴もイロイロある (ここ,ちょっと重要) パターン自身の性質 ? オレンジの画素数→多い ? 青の画素数→小 ? 円形度→高い ? 線対称度→高い ? 模様→細かい …. 他のパターンとの関係 ? 「車」との類似度→低 ? 「リンゴ」との類似度→高 ? 「猿」との類似度→低 ? 「柿」との類似度→高 … 他者との類似度も 特徴になる!
- 16. ところで,特徴もイロイロある (ここ,ちょっと重要) パターン自身の性質 ? オレンジの画素数→多い ? 青の画素数→小 ? 円形度→高い ? 線対称度→高い ? 模様→細かい …. 他のパターンとの関係 ? 「車」との類似度→低 ? 「リンゴ」との類似度→高 ? 「猿」との類似度→低 ? 「柿」との類似度→高 … 僕って, 身長が170cm, 体重が62km, 100m走が12.4秒, ラーメン替玉が3杯... 自分自身に 関する量で 自分を特徴づけ 僕って, 俳優Aに「やや似」, 俳優Bに「激似」 俳優Cに「全然似てない」, 俳優Dも「全然似てない」... 他者との 関係で 自分を特徴づけ どっちがイイとか悪いとかじゃなく, 単に特徴づけには色々あるってこと
- 22. ニューロンの計算モデル https://commons.wikimedia.org/ 入力 g ? ?xgx 出力 1x jx dx 1w jw dw g ? ?xg 重み 関数
- 23. ニューロンの計算モデル: もうちょっとキチッと Σ ? ?xg 1x jx dx 1 …… b ? ?bf bxwfg T d j jj ?? ? ? ? ? ? ? ? ? ?? ?? xw x 1 )( x 1w jw dw f f: 非線形関数 入力 出力 重み
- 24. キチッとしたいけど, 面倒くさそうなものは考えたくない Σ ? ?xg 1x jx dx 1 …… b x 1w jw dw f f: 非線形関数 OK, 忘れよう ? ?bf bxwfg T d j jj ?? ? ? ? ? ? ? ? ? ?? ?? xw x 1 )(
- 25. 結構簡単になった. でもまだ面倒そうなものが… Σ ? ?xg 1x jx dx 1 …… b x 1w jw dwOK, 忘れよう ?? ?? d j jj bxwg 1 )(x
- 26. ずいぶん簡単になった. あれ,これ見たことある? Σ 1x jx dx …… xwT おお,これは2つの ベクトルの内積じゃん (d次元ベクトルwとxのd個の要素それぞれを 掛け合わせていき,最後に全部足す. ちなみにそれを一気に表したものが ? ? ?) x 1w jw dw w xw x T d j jj xwg ? ? ?? 1 )( 入力 重み