Experimental Xylophone. Study of transverse vibrations in a thin metal bar
Download as PPSX, PDF
0 likes452 views
Study of transverse vibrations in a thin metal bar. Fundametal and harmonics. Mathematical modeling on an experimental xylophone, contruction and testing. This was a school project.
Experimental Xylophone. Study of transverse vibrations in a thin metal bar
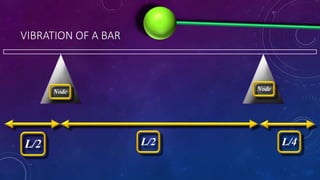
- 5. VIBRATION OF A BAR L/2 L/4L/2 Node Node
- 6. VIBRATION OF A BAR Node Node
- 7. VIBRATION OF A BAR Node Node
- 8. VIBRATION OF A BAR Node Node
- 9. VIBRATION OF A BAR Node Node
- 10. VIBRATION OF A BAR Node Node
- 11. VIBRATION OF A BAR Node Node = . This transverse vibration mode is the fundamental The frequency F is Y is the young modulus = 69Gpa for Al is the bulk density = 2700kg/m3 for Al T is the thickness = 0.00635m 村 L is the length of the bar = 0.355 for C4
- 12. VIBRATION OF A BAR Node Node All the transverse modes are expressed as: = 8 12 2 3.0112, 52 , 72, , 2 + 1 2,
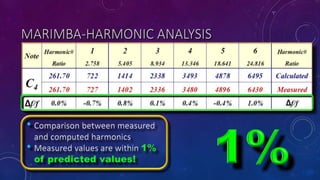
- 13. VIBRATION OF A BAR Node Node The ratios for the harmonics are: 0 1 2 3 4 5 6 Harmonic# 1 2.758 5.405 8.934 13.346 18.641 24.816 Ratio The ratios of harmonics are not whole or rational numbers. Therefore, a solid bar will not produce a harmonious sound.
- 16. MARIMBA COMPARISON BETWEEN THEORETICAL VALUES AND ACTUAL MEASUREMENTS F0 (Hz) Just Scale F0 (Hz) Measured 261.63 261.70 327.03 327.00 392.44 392.30 523.25 523.50 C4 C5 E4 G4