Population dynamics
- 1. Chapter 52 Population Ecology Population Dynamics
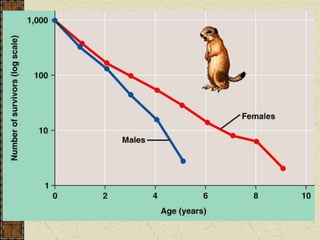
- 2. Survivorship Curves Data in a life table can be represented graphically by a survival curve. Curve usually based on a standardized population of 1000 individuals and the X- axis scale is logarithmic.
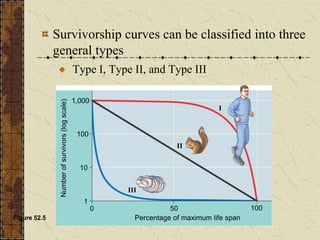
- 4. Survivorship curves can be classified into three general types Type I, Type II, and Type III Figure 52.5 I II III 50 100 0 1 10 100 1,000 Percentage of maximum life span Number of survivors (log scale)
- 5. Type I curve Type I curve typical of animals that produce few young but care for them well (e.g. humans, elephants). Death rate low until late in life where rate increases sharply as a result of old age (wear and tear, accumulation of cellular damage, cancer).
- 6. Type II curve Type II curve has fairly steady death rate throughout life (e.g. rodents). Death is usually a result of chance processes over which the organism has little control (e.g. predation)
- 7. Type III curve Type III curve typical of species that produce large numbers of young which receive little or no care (e.g. Oyster). Survival of young is dependent on luck. Larvae released into sea have only a small chance of settling on a suitable substrate. Once settled however, prospects of survival are much better and a long life is possible.
- 8. Population growth Occurs when birth rate exceeds death rate (duh!) Organisms have enormous potential to increase their populations if not constrained by mortality. Any organism could swamp the planet in a short time if it reproduced without restraint.
- 9. Per Capita Rate of Increase If immigration and emigration are ignored, a population’s growth rate (per capita increase) equals the per capita birth rate minus the per capita death rate
- 10. Equation for population growth is ΔN/Δt = bN-dN Where N = population size, b is per capita birth rate and d is per capita death rate. ΔN/Δt is change in population N over a small time period t.
- 11. The per capita rate of population increase is symbolized by r. r = b-d. r indicates whether a population is growing (r >0) or declining (r<0).
- 12. Ecologists express instantaneous population growth using calculus. Zero population growth occurs when the birth rate equals the death rate r = 0. The population growth equation can be expressed as dN dt  rN
- 13. Exponential population growth (EPG) Describes population growth in an idealized, unlimited environment. During EPG the rate of reproduction is at its maximum.
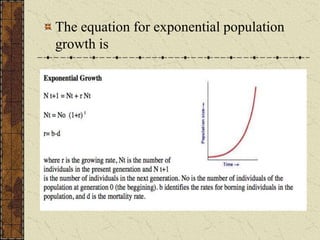
- 14. The equation for exponential population growth is dN dt  rmaxN
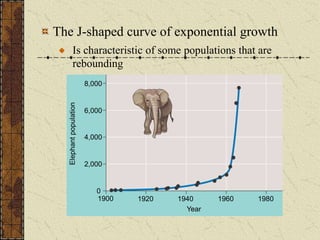
- 15. The J-shaped curve of exponential growth Is characteristic of some populations that are rebounding 1900 1920 1940 1960 1980 Year 0 2,000 4,000 6,000 8,000 Elephant population
- 16. Logistic Population Growth Exponential growth cannot be sustained for long in any population. A more realistic population model limits growth by incorporating carrying capacity. Carrying capacity (K) is the maximum population size the environment can support
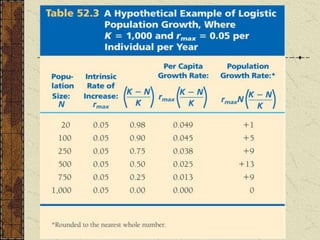
- 17. The Logistic Growth Model In the logistic population growth model the per capita rate of increase declines as carrying capacity is approached. We construct the logistic model by starting with the exponential model and adding an expression that reduces the per capita rate of increase as N increases
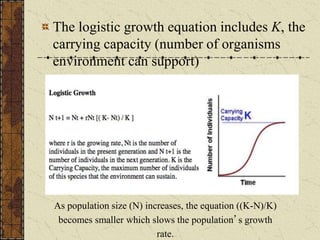
- 18. The logistic growth equation includes K, the carrying capacity (number of organisms environment can support) As population size (N) increases, the equation ((K-N)/K) becomes smaller which slows the population’s growth rate.
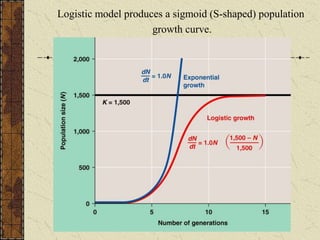
- 20. Logistic model produces a sigmoid (S-shaped) population growth curve.
- 21. Logistic model predicts different per capita growth rates for populations at low and high density. At low density population growth rate driven primarily by r the rate at which offspring can be produced. At low density population grows rapidly. At high population density population growth is much slower as density effects exert their effect.
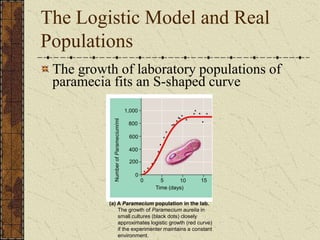
- 22. 800 600 400 200 0 Time (days) 0 5 10 15 (a) A Paramecium population in the lab. The growth of Paramecium aurelia in small cultures (black dots) closely approximates logistic growth (red curve) if the experimenter maintains a constant environment. 1,000 Number of Paramecium/ml The Logistic Model and Real Populations The growth of laboratory populations of paramecia fits an S-shaped curve
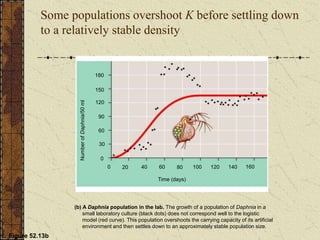
- 23. Some populations overshoot K before settling down to a relatively stable density Figure 52.13b 180 150 0 120 90 60 30 Time (days) 0 160 140 120 80 100 60 40 20 Number of Daphnia/50 ml (b) A Daphnia population in the lab. The growth of a population of Daphnia in a small laboratory culture (black dots) does not correspond well to the logistic model (red curve). This population overshoots the carrying capacity of its artificial environment and then settles down to an approximately stable population size.
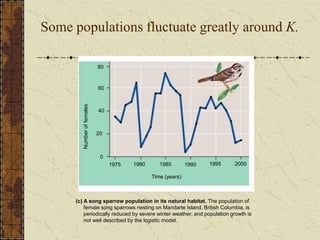
- 24. Some populations fluctuate greatly around K. 0 80 60 40 20 1975 1980 1985 1990 1995 2000 Time (years) Number of females (c) A song sparrow population in its natural habitat. The population of female song sparrows nesting on Mandarte Island, British Columbia, is periodically reduced by severe winter weather, and population growth is not well described by the logistic model.
- 25. K-selection, or density-dependent selection Selects for life history traits that are sensitive to population density r-selection, or density-independent selection Selects for life history traits that maximize reproduction
- 26. The concepts of K-selection and r-selection have been criticized by ecologists as oversimplifications. Most organisms exhibit intermediate traits or can adjust their behavior to different conditions.