Thermal strain and Thermal Stress (in Japanese)
Download as pptx, pdf0 likes143 views
Text book for the mechanics of materials [Part IX] Thermal strain and Thermal Stress note: Your feedback is welcome!
1 of 6
Download to read offline

![熱ひずみ(Thermal Strain)
収縮
ΔT ( < 0)
l
膨張
ΔT ( > 0)
l ΔlT+
αΔlT ΔTl=
: 線膨張係数 [1/K]α
εT =
l
ΔlT
= α ΔT
熱ひずみ
材料の温度変化によって生じるひずみ](https://image.slidesharecdn.com/09thermalstrainandthermalstress-170610073258/85/Thermal-strain-and-Thermal-Stress-in-Japanese-3-320.jpg)
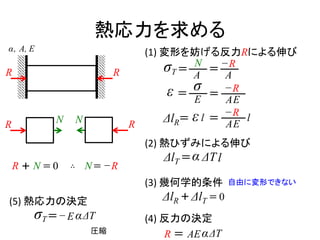
![まとめ
1. 熱ひずみと熱応力を説明できる
2.熱ひずみと熱応力を求めることができる
熱ひずみ: 温度変化により生じるひずみ
: 線膨張係数 [1/K]α
熱応力: 温度変化により生じる変形が妨げられることで生じる応力
(1) 変形を妨げる反力による伸びを求める
(2) 熱ひずみによる伸びを求める
(3) 幾何学的条件を考える
熱応力を求める
熱ひずみを求める
εT = α ΔT
(4) 反力を決定する ( (2),(3)の連立方程式を解く )
(5) 熱応力を決定する](https://image.slidesharecdn.com/09thermalstrainandthermalstress-170610073258/85/Thermal-strain-and-Thermal-Stress-in-Japanese-6-320.jpg)
Ad
Recommended
【材料力学】主応力と主せん断応力 (II-09-2 2020)
【材料力学】主応力と主せん断応力 (II-09-2 2020)Kazuhiro Suga
?
【目標】
1. 2次元応力状態で任意面の応力を計算できる
2. 主応力/主せん断応力を決定できる
3. 主応力面/主せん断応力面の幾何的関係を説明できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】3次元空間のひずみ (II-08-1 2020)
【材料力学】3次元空間のひずみ (II-08-1 2020)Kazuhiro Suga
?
1. 垂直ひずみと変位の関係を導出できる
2. せん断ひずみと変位の関係を導出できる
3. ひずみテンソルを説明できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】3次元空間の応力 (II-07-1 2020)
【材料力学】3次元空間の応力 (II-07-1 2020)Kazuhiro Suga
?
【目標】
1. 3次元空間における応力の定義を説明できる
2. 3次元空間における応力状態を説明できる
3. 応力テンソルを説明できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】相反定理 (II-05-1 2020)
【材料力学】相反定理 (II-05-1 2020)Kazuhiro Suga
?
【目標】
1. 複数荷重が作用する はり の弾性ひずみエネルギーを計算できる
2. Betti および Maxwellの相反定理を説明できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】座屈荷重 (II-03-2 2020)
【材料力学】座屈荷重 (II-03-2 2020)Kazuhiro Suga
?
【目標】
1. 支持条件から境界条件を決定できる
2. 座屈荷重を決定できる
3. 端末条件係数と座屈長さを説明できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】座屈 (II-03-1 2020)
【材料力学】座屈 (II-03-1 2020)Kazuhiro Suga
?
【目標】
1. 座屈の特徴を説明できる
2. 座屈方程式を導出できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】特別な丸棒のねじり (II-02-1 2020)
【材料力学】特別な丸棒のねじり (II-02-1 2020)Kazuhiro Suga
?
【目標】
1. 中空丸棒の欠点と利点を説明できる
2. 中空丸棒の有効性を評価できる
3. 軸径が変化する丸棒のねじれ角を計算できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】ねじり剛性 (II-01-3 2020)
【材料力学】ねじり剛性 (II-01-3 2020)Kazuhiro Suga
?
【目標】
1. トルクとせん断応力の関係を導出できる
2. ねじり剛性を説明できる
3. 断面二次極モーメントを説明できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】重ね合わせの原理を用いた不静定はりの解法 (I-11-3 2020)
【材料力学】重ね合わせの原理を用いた不静定はりの解法 (I-11-3 2020)Kazuhiro Suga
?
【目標】
1. 重ね合わせの原理を用いた解法手順を説明できる
2. 不静定問題を静定問題に分解できる
3. 重ね合わせの原理を用いて不静定問題が解ける【材料力学】幾何学的条件を用いた不静定はりの解法 (I-11-2 2020)
【材料力学】幾何学的条件を用いた不静定はりの解法 (I-11-2 2020)Kazuhiro Suga
?
【目標】
1. 幾何学的条件を用いた解法手順を説明できる
2. 幾何学的条件を決定できる
3. 幾何学的条件を用いて不静定問題が解ける【材料力学】はり のたわみとたわみ角の求め方 (I-10-2 2020)
【材料力学】はり のたわみとたわみ角の求め方 (I-10-2 2020)Kazuhiro Suga
?
【目標】
1. たわみとたわみ角を求める手順を説明できる
2. 集中荷重が作用する単純支持はり のたわみとたわみ角を求めることができる【材料力学】はり のたわみ (I-10-1 2020)
【材料力学】はり のたわみ (I-10-1 2020)Kazuhiro Suga
?
【目標】
1. たわみ曲線?たわみ角?たわみを説明できる
2. たわみの式を説明できる
3. たわみ と たわみ角の求め方を説明できる【材料力学】はり (I-08-1 2020)
【材料力学】はり (I-08-1 2020)Kazuhiro Suga
?
【目標】
1. はり の役割を説明できる
2. はり に曲げを引き起こす荷重を説明できる
3. 単純支持はりと片持ちはりを説明できる
【材料力学】(補足)仮想切断 (I-note-virtual_cut 2020)
【材料力学】(補足)仮想切断 (I-note-virtual_cut 2020)Kazuhiro Suga
?
?切断面に生じる力とモーメントの図示方法を正確に覚える
?2次元の仮想断面の力とモーメントは3成分で表現できる
【材料力学】(補足)力のモーメント (I-note-moment 2020)
【材料力学】(補足)力のモーメント (I-note-moment 2020)Kazuhiro Suga
?
?力が作用すると物体は回転する
?物体を回転させる作用を「力のモーメント」と呼ぶ
?力のモーメントは「距離」と 「力」の外積で定義される
?力のモーメントはベクトルである
?力のモーメント」の計算はベクトル成分を図示すれば間違えない
【材料力学】熱ひずみと熱応力 (I-07-3 2020)
【材料力学】熱ひずみと熱応力 (I-07-3 2020)Kazuhiro Suga
?
【目標】
1. 温度変化による変形を考慮すべき理由を説明できる
2. 熱ひずみと熱応力を説明できる
3. 熱ひずみと熱応力を求めることができる【材料力学】フックの法則 (I-05-1 2020)
【材料力学】フックの法則 (I-05-1 2020)Kazuhiro Suga
?
【目標】
1. フックの法則を説明できる
2. 応力ーひずみ線図との関係を説明できる
3. 内力および変形との関係を説明できる【材料力学】内力の決定 (I-02-2 2020)
【材料力学】内力の決定 (I-02-2 2020)Kazuhiro Suga
?
【目標】
1. 内力の決定手順を説明できる
2. 一方向引張荷重が作用する棒の内力を決定できる
3. 荷重条件が途中で変化する棒の内力を決定できる
More Related Content
More from Kazuhiro Suga (20)
【材料力学】座屈 (II-03-1 2020)
【材料力学】座屈 (II-03-1 2020)Kazuhiro Suga
?
【目標】
1. 座屈の特徴を説明できる
2. 座屈方程式を導出できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】特別な丸棒のねじり (II-02-1 2020)
【材料力学】特別な丸棒のねじり (II-02-1 2020)Kazuhiro Suga
?
【目標】
1. 中空丸棒の欠点と利点を説明できる
2. 中空丸棒の有効性を評価できる
3. 軸径が変化する丸棒のねじれ角を計算できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】ねじり剛性 (II-01-3 2020)
【材料力学】ねじり剛性 (II-01-3 2020)Kazuhiro Suga
?
【目標】
1. トルクとせん断応力の関係を導出できる
2. ねじり剛性を説明できる
3. 断面二次極モーメントを説明できる
/KazuhiroSuga/clipboards/i-2020
/KazuhiroSuga/clipboards/ii-2020
【材料力学】重ね合わせの原理を用いた不静定はりの解法 (I-11-3 2020)
【材料力学】重ね合わせの原理を用いた不静定はりの解法 (I-11-3 2020)Kazuhiro Suga
?
【目標】
1. 重ね合わせの原理を用いた解法手順を説明できる
2. 不静定問題を静定問題に分解できる
3. 重ね合わせの原理を用いて不静定問題が解ける【材料力学】幾何学的条件を用いた不静定はりの解法 (I-11-2 2020)
【材料力学】幾何学的条件を用いた不静定はりの解法 (I-11-2 2020)Kazuhiro Suga
?
【目標】
1. 幾何学的条件を用いた解法手順を説明できる
2. 幾何学的条件を決定できる
3. 幾何学的条件を用いて不静定問題が解ける【材料力学】はり のたわみとたわみ角の求め方 (I-10-2 2020)
【材料力学】はり のたわみとたわみ角の求め方 (I-10-2 2020)Kazuhiro Suga
?
【目標】
1. たわみとたわみ角を求める手順を説明できる
2. 集中荷重が作用する単純支持はり のたわみとたわみ角を求めることができる【材料力学】はり のたわみ (I-10-1 2020)
【材料力学】はり のたわみ (I-10-1 2020)Kazuhiro Suga
?
【目標】
1. たわみ曲線?たわみ角?たわみを説明できる
2. たわみの式を説明できる
3. たわみ と たわみ角の求め方を説明できる【材料力学】はり (I-08-1 2020)
【材料力学】はり (I-08-1 2020)Kazuhiro Suga
?
【目標】
1. はり の役割を説明できる
2. はり に曲げを引き起こす荷重を説明できる
3. 単純支持はりと片持ちはりを説明できる
【材料力学】(補足)仮想切断 (I-note-virtual_cut 2020)
【材料力学】(補足)仮想切断 (I-note-virtual_cut 2020)Kazuhiro Suga
?
?切断面に生じる力とモーメントの図示方法を正確に覚える
?2次元の仮想断面の力とモーメントは3成分で表現できる
【材料力学】(補足)力のモーメント (I-note-moment 2020)
【材料力学】(補足)力のモーメント (I-note-moment 2020)Kazuhiro Suga
?
?力が作用すると物体は回転する
?物体を回転させる作用を「力のモーメント」と呼ぶ
?力のモーメントは「距離」と 「力」の外積で定義される
?力のモーメントはベクトルである
?力のモーメント」の計算はベクトル成分を図示すれば間違えない
【材料力学】熱ひずみと熱応力 (I-07-3 2020)
【材料力学】熱ひずみと熱応力 (I-07-3 2020)Kazuhiro Suga
?
【目標】
1. 温度変化による変形を考慮すべき理由を説明できる
2. 熱ひずみと熱応力を説明できる
3. 熱ひずみと熱応力を求めることができる【材料力学】フックの法則 (I-05-1 2020)
【材料力学】フックの法則 (I-05-1 2020)Kazuhiro Suga
?
【目標】
1. フックの法則を説明できる
2. 応力ーひずみ線図との関係を説明できる
3. 内力および変形との関係を説明できる【材料力学】内力の決定 (I-02-2 2020)
【材料力学】内力の決定 (I-02-2 2020)Kazuhiro Suga
?
【目標】
1. 内力の決定手順を説明できる
2. 一方向引張荷重が作用する棒の内力を決定できる
3. 荷重条件が途中で変化する棒の内力を決定できる
Thermal strain and Thermal Stress (in Japanese)
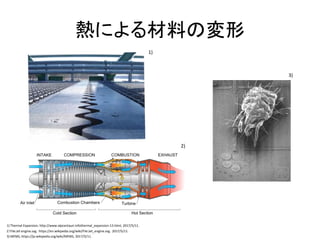
- 2. 熱による材料の変形 1) Thermal Expansion, http://www.alpcentauri.infothermal_expansion-13.html, 2017/5/11. 1) 3) MEMS, https://ja.wikipedia.org/wiki/MEMS, 2017/5/11. 3) 2)File:Jet engine.svg,https://en.wikipedia.org/wiki/File:Jet_engine.svg,2017/5/11. 2)
- 3. 熱ひずみ(Thermal Strain) 収縮 ΔT ( < 0) l 膨張 ΔT ( > 0) l ΔlT+ αΔlT ΔTl= : 線膨張係数 [1/K]α εT = l ΔlT = α ΔT 熱ひずみ 材料の温度変化によって生じるひずみ
- 4. 熱応力(Thermal Stress) 自由に変形できる場合 αΔlT ΔTl= ΔT 軸方向に力は作用しない σT = 0 自由に変形できない場合 変形を妨げる反力が作用する RR σT = 0 熱応力 温度変化により生じる変形が妨げられることで生じる応力
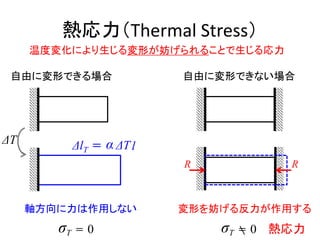
- 5. 熱応力を求める RR R N N R R = 0+ N =N∴ R? ε σ= E = AE R? εΔlR= l = AE R? l (1) 変形を妨げる反力Rによる伸び αΔlT ΔTl= (2) 熱ひずみによる伸び ΔlR ΔlT+ = 0 (3) 幾何学的条件 自由に変形できない α,A, E R = αΔTAE = N A = A R?σT (4) 反力の決定σT= αΔTE? (5) 熱応力の決定 圧縮
- 6. まとめ 1. 熱ひずみと熱応力を説明できる 2.熱ひずみと熱応力を求めることができる 熱ひずみ: 温度変化により生じるひずみ : 線膨張係数 [1/K]α 熱応力: 温度変化により生じる変形が妨げられることで生じる応力 (1) 変形を妨げる反力による伸びを求める (2) 熱ひずみによる伸びを求める (3) 幾何学的条件を考える 熱応力を求める 熱ひずみを求める εT = α ΔT (4) 反力を決定する ( (2),(3)の連立方程式を解く ) (5) 熱応力を決定する