05 hephuongtrinh
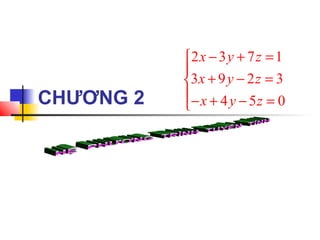
- 1. CHÆŊÆ NG 2 2 3 7 1 3 9 2 3 4 5 0 x y z x y z x y z â + =ïĢą ïĢī + â =ïĢē ïĢīâ + â =ïĢģ
- 2. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh
- 3. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh
- 4. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh
- 5. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh ïŪ Và dáŧĨ: Cho ģóáŧ phÆ°ÆĄng trÃŽnh 1 2 3 4 1 2 3 4 1 2 3 4 2 3 4 2 3 5 2 2 3 4 0 3 8 5 3 2 4 2 7 9 x x x x x x x x x x x x x x x â + â =ïĢą ïĢīâ â + + =ïĢī ïĢē + â + = âïĢī ïĢī â + â =ïĢģ
- 6. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh
- 7. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh ïŪ Và dáŧĨ: Cho ģóáŧ phÆ°ÆĄng trÃŽnh 1 2 3 4 1 2 3 4 1 2 3 4 2 3 4 2 3 5 2 2 3 5 1 2 3 4 0 1 2 3 4 3 8 5 3 2 3 8 5 3 0 4 2 74 2 7 9 x x x x x x x x A x x x x x x x â + â = â âïĢą ïĢŪ ïĢđ ïĢī ïĢŊ ïĢšâ â + + = â âïĢī ïĢŊ ïĢšâ =ïĢē ïĢŊ ïĢš+ â + = â âïĢī ïĢŊ ïĢšïĢī â ââ + â = ïĢ° ïĢŧïĢģ
- 8. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh
- 9. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh ïŪ Và dáŧĨ: Cho ģóáŧ phÆ°ÆĄng trÃŽnh 1 2 3 4 1 2 3 4 1 2 3 4 2 3 4 2 3 5 2 2 2 3 4 0 0 3 8 5 3 2 2 94 2 7 9 x x x x x x x x B x x x x x x x â + â =ïĢą ïĢŪ ïĢđ ïĢī ïĢŊ ïĢšâ â + + =ïĢī ïĢŊ ïĢšâ =ïĢē ïĢŊ ïĢš+ â + = â âïĢī ïĢŊ ïĢšïĢī â + â = ïĢ° ïĢŧïĢģ
- 10. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh
- 11. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh
- 12. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh ïŪ Và dáŧĨ: Cho ģóáŧ phÆ°ÆĄng trÃŽnh 1 2 3 4 1 2 3 4 1 2 3 4 2 3 4 2 3 5 2 2 3 4 0 3 8 5 3 2 4 2 7 9 2 3 5 1 2 1 2 3 4 0 3 8 5 3 2 0 4 2 7 9 bs x x x x x x x x x x x x x x x A â + â =ïĢą ïĢīâ â + + =ïĢī ïĢē + â + = âïĢī ïĢī â + â =ïĢģ â âïĢŪ ïĢđ ïĢŊ ïĢšâ âïĢŊ ïĢšâ = ïĢŊ ïĢšâ â ïĢŊ ïĢš â âïĢ° ïĢŧ
- 13. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh
- 14. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh ïŪ Và dáŧĨ: 2 7 1 9 3 1 4 0 5 9 2 5 x y z ïĢŪ ïĢđ ïĢŪ ïĢđ ïĢŪ ïĢđ ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢšâ =ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢšïĢ° ïĢŧ ïĢ° ïĢŧ ïĢ° ïĢŧ 2 7 9 3 4 0 5 9 2 5 x y z x y z x y z + + =ïĢą ïĢī â â + =ïĢē ïĢī + + =ïĢģ
- 15. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame
- 16. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame
- 17. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame
- 18. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame
- 19. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame
- 20. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame ïŪ Và dáŧĨ: GiášĢi ģóáŧ phÆ°ÆĄng trÃŽnh tuyášŋn tÃnh sau:
- 21. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame
- 22. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame
- 23. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame
- 24. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame ïŪ Bà i tášp: GiášĢi ģóáŧ phÆ°ÆĄng trÃŽnh sau: 1 2 3 1 2 3 1 2 3 2 1 2 3 5 3 2 1 x x x x x x x x x â + =ïĢą ïĢī + â =ïĢē ïĢī â + =ïĢģ 1 1 2 2 1 3 3 2 1 D â = â â 1 1 1 2 5 1 3 1 2 1 D â = â â 2 1 1 2 2 5 3 3 1 1 D = â 3 1 1 1 2 1 5 3 2 1 D â = â = -19= -19 = -29= -29 = -9= -9 = -8= -8
- 25. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ Grame 1 1 2 2 3 3 19 8 29 8 9 8 D x D D x D D x D â= = â â= = â â= = â
- 26. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss ïŪ CÃĄc phÃĐp biášŋn Äáŧi tÆ°ÆĄng ÄÆ°ÆĄng ģóáŧ phÆ°ÆĄng trÃŽnhCÃĄc phÃĐp biášŋn Äáŧi tÆ°ÆĄng ÄÆ°ÆĄng ģóáŧ phÆ°ÆĄng trÃŽnh ï NhÃĒn máŧt sáŧ ( ) và o 2 vášŋ cáŧ§a 1 PT cáŧ§aNhÃĒn máŧt sáŧ ( ) và o 2 vášŋ cáŧ§a 1 PT cáŧ§a ģóáŧ.ģóáŧ. ï Äáŧi cháŧ hai PT cáŧ§a ģóáŧ.Äáŧi cháŧ hai PT cáŧ§a ģóáŧ. ï NhÃĒn máŧt sáŧ ( ) và o máŧt PT ráŧi cáŧng và oNhÃĒn máŧt sáŧ ( ) và o máŧt PT ráŧi cáŧng và o PT khÃĄc cáŧ§a ģóáŧ.PT khÃĄc cáŧ§a ģóáŧ. 0Îŧ â 0Îŧ â 1 2 3 2 2 5 x y z x y z x y z â + =ïĢą ïĢī + â =ïĢē ïĢī + + =ïĢģ 1 2 3 2 2 4 2 10 x y z x y z x y z â + =ïĢą ïĢī â + â =ïĢē ïĢī + + =ïĢģ 2 4 2 10 1 2 3 2 x y z x y z x y z â + =ïĢą ïĢī â + + =ïĢē ïĢī + â =ïĢģ
- 27. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss ïŪ NhÆ° vášy cÃĄc phÃĐp biášŋn Äáŧi tÆ°ÆĄng ÄÆ°ÆĄng ģóáŧ PT chÃnh là cÃĄc phÃĐp BÄSC trÊn dÃēng cáŧ§a ma trášn báŧ sung tÆ°ÆĄng áŧĐng..
- 28. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss XÃĐt ģóáŧ phÆ°ÆĄng trÃŽnh táŧng quÃĄt sau:
- 29. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss Ta cÃģ ma trášn báŧ sung tÆ°ÆĄng áŧĐng
- 30. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 11 12 1 1 1 22 2 2 2 ' ' ... ' ... ' ' 0 ' ... ' ... ' ' ... ... ... ... ... ... ... ' 0 0 ... ' ... ' ' 0 0 ... 0 ... 0 .. .. .. .. .. .. .. 0 0 ... 0 ... 0 0 r n r n r r r n r a a a a b a a a b A a a b k ïĢŪ ïĢđ ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš = ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢ° ïĢŧ Bášąng cÃĄc phÃĐp B ÄSC chuyáŧn ma trášn báŧ sung váŧ dᚥng:
- 31. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss Ma trášn Aâ tÆ°ÆĄng áŧĐng cho ta ģóáŧ PTTT 11 1 12 2 1 1 1 22 2 2 2 2 1 2 ' ' ... ' ... ' ' ' ... ' ... ' ' ... ... ... ... ... ' ... ' ' 0 0 ... 0 ... 0 r r n n r r n n rr r rn n r r n a x a x a x a x b a x a x a x b a x a x b x x x x k ïĢą + + + + + = ïĢī + + + + =ïĢī ïĢī ïĢē ïĢī + + = ïĢī ïĢī + + + + + =ïĢģ
- 32. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss Khi ÄÃģ ta cÃģ: ïŪ 1. Nášŋu thÃŽ PT tháŧĐ (r +1) vÃī nghiáŧm suy ra ģóáŧ PT vÃī nghiáŧm. ïŪ 2. Nášŋu thÃŽ ģóáŧ cÃģ nghiáŧm: ï a. Nášŋu r = n (sáŧ ášĐn) thÃŽ ģóáŧ PT cÃģ nghiáŧn duy nhášĨt. ï b. Nášŋu r < n (sáŧ ášĐn) thÃŽ ģóáŧ PT cÃģ vÃī sáŧ nghiáŧm, pháŧĨ thuáŧc và o (n â r) tham sáŧ. 0k â 0k =
- 33. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss a. Khi r = n (sáŧ ášĐn) thÃŽ ģóáŧ PT (II) viášŋt dÆ°áŧi dᚥng: 11 1 12 2 1 1 1 22 2 2 2 2 ' ' ... ' ... ' ' ' ... ' ... ' ' ... ... ... ... ... ' ... ' ' ... ... ... ' ' r r n n r r n n rr r rn n r nn n n a x a x a x a x b a x a x a x b a x a x b a x b + + + + + =ïĢą ïĢī + + + + =ïĢī ïĢīïĢī ïĢē + + =ïĢī ïĢī ïĢī =ïĢīïĢģ
- 34. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss b. Khi r < n ta chuyáŧn (n â r) ášĐn sang vášŋ phášĢi cáŧ§a ģóáŧ PT ta ÄÆ°áŧĢc ģóáŧ PT sau: Ta xem cÃĄc ášĐn áŧ vášŋ phášĢi là cÃĄc tham sáŧ, sau ÄÃģ giášĢi cÃĄc ášĐn cÃēn lᚥi theo cÃĄc tham sáŧ ÄÃģ. 11 1 12 2 1 1( 1) 1 1 1 22 2 2 2( 1) 1 2 2 ( 1) 1 ' ' ... ' ' ... ' ' ' ... ' ' ... ' ' ... ... ... ... ... ' ' ... ' ' r r r r n n r r r r n n rr r r r r rn n r a x a x a x a x a x b a x a x a x a x b a x a x a x b + + + + + + + + + = â â â +ïĢą ïĢī + + = â â â +ïĢī ïĢē ïĢī ïĢī = â â â +ïĢģ
- 35. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 2 3 5 2 5 3 5 3 3 5 5 3 2(5 3) 7 1 5 3 5 3 7 1 6 5 3, 1 2 1 13 2 7 2 x y z x y z y z y z x z z x z y z y z x m x y m m y z m z x m y z â + = â = âïĢą ïĢą âïĢē ïĢē â + = â = âïĢģ ïĢģ = â + â = âïĢą ïĢą â âïĢē ïĢē = â = âïĢģ ïĢģ = â =ïĢą ïĢą ïĢī ïĢī = â = â =ïĢē ïĢē ïĢī ïĢī= =ïĢģ ïĢģ =ïĢą ïĢī = â =ïĢē ïĢī =ïĢģ
- 36. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 2 3 5 2 5 3 5 4 3 3 5 4 x y z t x y z t y z t y z t â + â = â = â +ïĢą ïĢą âïĢē ïĢē â + + = â = â âïĢģ ïĢģ
- 37. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss
- 38. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 2 1 4 1 5 1 2 4 h h h h h h â + â ïĢ§ïĢ§ ïĢ§â âĶ. ï
- 39. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss
- 40. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss Vášy ģóáŧ phÆ°ÆĄng trÃŽnh
- 41. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss
- 42. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss
- 43. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss sáŧ dáŧĨng cÃĄc phÃĐp biášŋn Äáŧi sÆĄ cášĨp ÄÆ°a ma trášn báŧ sung váŧ dᚥng ma trášn hÃŽnh thang: ...bs A â â
- 44. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss
- 45. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss
- 46. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss
- 47. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss ïŪ Bà i Tášp: GiášĢi ģóáŧ phÆ°ÆĄng trÃŽnh: 1 2 3 4 1 2 3 4 2 3 4 1 2 3 4 2 2 2 3 2 2 3 4 5 1 2 3 0 x x x x x x x x x x x x x x x â + + =ïĢą ïĢī + â â =ïĢī ïĢē + â = âïĢī ïĢīâ + + â =ïĢģ ïĢī ïĢī ïĢģ ïĢī ïĢī ïĢē ïĢą â= = â= = â 1 0 2 1 4 3 2 1 x x x x
- 48. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 2 1 4 1 2 1 1 2 1 2 0 3 7 4 2 0 3 4 5 1 0 0 4 2 2 h h h h â + âïĢŪ ïĢđ ïĢŊ ïĢšâ â â ïĢŊ ïĢšïĢ§ïĢ§ïĢ§â ïĢŊ ïĢšâ â ïĢŊ ïĢš âïĢ° ïĢŧ 3 2 1 1 2 1 2 0 3 7 4 2 0 0 11 1 1 0 0 4 2 2 h hâ âïĢŪ ïĢđ ïĢŊ ïĢšâ â â ïĢŊ ïĢšïĢ§ïĢ§ïĢ§â ïĢŊ ïĢšâ ïĢŊ ïĢš âïĢ° ïĢŧ 1 1 2 1 2 2 1 3 2 2 0 3 4 5 1 1 1 2 3 0 âïĢŪ ïĢđ ïĢŊ ïĢšâ â ïĢŊ ïĢš ïĢŊ ïĢšâ â ïĢŊ ïĢš â âïĢ° ïĢŧ 4 311 4 1 1 2 1 2 0 3 7 4 2 0 0 11 1 1 0 0 0 18 18 h hâ âïĢŪ ïĢđ ïĢŊ ïĢšâ â â ïĢŊ ïĢšïĢ§ïĢ§ïĢ§ïĢ§â ïĢŊ ïĢšâ ïĢŊ ïĢš âïĢ° ïĢŧ
- 49. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss ïŪ Bà i Tášp: GiášĢi ģóáŧ phÆ°ÆĄng trÃŽnh: 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 2 5 1 3 4 3 1 4 7 1 2 5 5 8 2 x x x x x x x x x x x x x x x x â â + =ïĢą ïĢīâ + + â = âïĢī ïĢē â + + â = âïĢī ïĢī â â + =ïĢģ 1 2 3 4 2 3 4 2 5 1 3 2 0 x x x x x x x â â + =ïĢą â ïĢē + + =ïĢģ
- 50. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss
- 51. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 11 12 1 1 1 22 2 2 2 ' ' ... ' ... ' ' 0 ' ... ' ... ' ' ... ... ... ... ... ... ... 0 0 ... ' ... ' ' 0 0 ... 0 ... 0 .. .. .. .. .. .. .. 0 0 ... 0 ... 0 0 r n r n bs r r r n r a a a a b a a a b A a a b k ïĢŪ ïĢđ ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš = ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢš ïĢ° ïĢŧ Bášąng cÃĄc phÃĐp B ÄSC chuyáŧn ma trášn báŧ sung váŧ dᚥng:
- 52. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss Khi ÄÃģ ta cÃģ: ïŪ 1. Nášŋu thÃŽ PT tháŧĐ (r +1) vÃī nghiáŧm suy ra ģóáŧ PT vÃī nghiáŧm. ïŪ 2. Nášŋu thÃŽ ģóáŧ cÃģ nghiáŧm: ï a. Nášŋu r = n (sáŧ ášĐn) thÃŽ ģóáŧ PT cÃģ nghiáŧn duy nhášĨt. ï b. Nášŋu r < n (sáŧ ášĐn) thÃŽ ģóáŧ PT cÃģ vÃī sáŧ nghiáŧm, pháŧĨ thuáŧc và o (n â r) tham sáŧ. 0k â 0k =
- 53. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 1 ( ) 3 ( ) 4bs m r A r A+ = â â = â = â 2 1 2 1 1 1 0 1 3 2 2 0 0 1 2 3 0 0 0 1 1 bs A m m âïĢŪ ïĢđ ïĢŊ ïĢš ïĢŊ ïĢš= ïĢŊ ïĢšâ â ïĢŊ ïĢš â âïĢ° ïĢŧ 1 ( ) ( ) 3bs m r A r A n+ = â = = < â Biáŧn luášn theo m sáŧ nghiáŧm cáŧ§a ģóáŧ: 2 2 1 3 2 2 2 3 ( 1) 1 x y z t y z t z t m t m + â + =ïĢą ïĢī + + =ïĢī ïĢē â â =ïĢī ïĢī â = âïĢģ Háŧ vÃī nghiáŧm Háŧ cÃģ VSN Háŧ cÃģ Ng duy nhášĨt1 ( ) ( )bs m r A r A n+ â Âą â = = â
- 54. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 2 2 1 2 5 3 0 2 3 3 1 x y z t x y z t y z t x y z mt + â + =ïĢą ïĢī + + + =ïĢī ïĢē â â =ïĢī ïĢī â + + =ïĢģ Bà i tášp: Biáŧn luášn theo m sáŧ nghiáŧm cáŧ§a ģóáŧ phÆ°ÆĄng trÃŽnh
- 55. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 1 2 1 2 1 0 1 5 3 2 0 0 7 0 5 0 0 0 7 77 43 bs A m âïĢŪ ïĢđ ïĢŊ ïĢšâ âïĢŊ ïĢšâ ïĢŊ ïĢšâ ïĢŊ ïĢš âïĢ° ïĢŧ Ma trášn báŧ sung sau khi biášŋn Äáŧi sÆĄ cášĨp 11 ( ) 3 ( ) 4bs m r A r A= â = < = â> ģóáŧ vÃī nghiáŧm 11 ( ) ( ) 4bs m r A r Aâ â = = â> ģóáŧ cÃģ nghiáŧm duy nhášĨt
- 56. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 2 3 0 2 5 2 1 2 3 1 x y z t x y z t y z at b x z t + + â =ïĢą ïĢī + + + =ïĢī ïĢē â + =ïĢī ïĢī + + =ïĢģ Bà i tášp: Biáŧn luášn theo a, b sáŧ nghiáŧm cáŧ§a ģóáŧ phÆ°ÆĄng trÃŽnh
- 57. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 1 2 1 3 0 0 1 0 7 1 0 0 1 20 3 0 0 0 13 2 bs A a b âïĢŪ ïĢđ ïĢŊ ïĢš ïĢŊ ïĢš= ïĢŊ ïĢš ïĢŊ ïĢš + +ïĢ° ïĢŧ 13 ( ) 4,a r Aâ â â => 2 ( ) 4bs b r AâĒ â â â = â Ma trášn báŧ sung sau khi biášŋn Äáŧi sÆĄ cášĨp 13 ( ) 3a r A= â â => ģóáŧ cÃģ vÃī sáŧ nghiáŧm2 ( ) 3bs b r AâĒ = â â = â ģóáŧ vÃī nghiáŧm ( ) 4bs b r Aâ â = ģóáŧ cÃģ nghiáŧm duy nhášĨt
- 58. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: GiášĢi ģóáŧ PT bášąng PP Gauss 3 2 1 2 3 2 3 4 2 1 x y z x y mz x y z + + =ïĢą ïĢī â + + =ïĢē ïĢī â + =ïĢģ Bà i tášp: Biáŧn luášn theo m sáŧ nghiáŧm cáŧ§a ģóáŧ phÆ°ÆĄng trÃŽnh
- 59. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt
- 60. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt
- 61. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt
- 62. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt
- 63. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt 11 12 1 21 22 2 1 2 .. 0 .. 0 .. .. .. .. .. .. 0 n nbs m m mn a a a a a a A a a a ïĢŪ ïĢđ ïĢŊ ïĢš ïĢŊ ïĢš= ïĢŊ ïĢš ïĢŊ ïĢš ïĢŊ ïĢšïĢ° ïĢŧ Khi biáŧn luášn cho ģóáŧ thuᚧn nhášĨt ta cháŧ quan tÃĒm hᚥng cáŧ§a ma trášn ģóáŧ sáŧ Nhášn xÃĐt: Trong ģóáŧ thuᚧn nhášĨt hᚥng cáŧ§a ma trášn ģóáŧ sáŧ luÃīn bášąng hᚥng cáŧ§a ma trášn báŧ sung
- 64. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt ïŪ Háŧ thuᚧn nhášĨt cháŧ cÃģ 2 trÆ°áŧng háŧĢp: ï Háŧ cÃģ nghiáŧm duy nhášĨt Hᚥng ma trášn ģóáŧ sáŧ bášąng sáŧ ášĐn cáŧ§a ģóáŧ phÆ°ÆĄng trÃŽnh ï Háŧ cÃģ vÃī sáŧ nghiáŧm Hᚥng ma trášn ģóáŧ sáŧ nháŧ hÆĄn sáŧ ášĐn cáŧ§a ģóáŧ phÆ°ÆĄng trÃŽnh
- 65. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt ïŪ Nášŋu ģóáŧ cÃģ nghiáŧm duy nhášĨt thÃŽ nghiáŧm duy nhášĨt ÄÃģ là nghiáŧm tᚧm thÆ°áŧng: (0,0,âĶ,0). ï Ta gáŧi ģóáŧ thuᚧn nhášĨt cháŧ cÃģ nghiáŧm tᚧm thÆ°áŧng. ïŪ Nášŋu ģóáŧ cÃģ vÃī sáŧ nghiáŧm thÃŽ lÚc ÄÃģ ngoà i nghiáŧm tᚧm thÆ°áŧng ģóáŧ cÃēn cÃģ nghiáŧm khÃĄc náŧŊa. ï Ta gáŧi ģóáŧ thuᚧn nhášĨt cÃģ nghiáŧm khÃīng tᚧm thÆ°áŧng.
- 66. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt
- 67. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt ïŪ Và dáŧĨ: TÃŽm m Äáŧ ģóáŧ phÆ°ÆĄng trÃŽnh sau cÃģ nghiáŧm khÃīng tᚧm thÆ°áŧng.
- 68. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt
- 69. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt
- 70. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt 1 2 1 0 3 1 0 0 2 A m âïĢŪ ïĢđ ïĢŊ ïĢšïĢ§ïĢ§ïĢ§ïĢ§âïĢŊ ïĢš ïĢŊ ïĢš+ïĢ° ïĢŧ 2 ( ) 3m r A= â â < Ta cÃģ: Biášŋn Äáŧi sÆĄ cášĨp Do ÄÃģ váŧi Vášy váŧi thÃŽ ģóáŧ cÃģ nghiáŧm khÃīng tᚧm thÆ°áŧng 2m =â
- 71. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt
- 72. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt ïŪ Và dáŧĨ: TÃŽm m Äáŧ ģóáŧ phÆ°ÆĄng trÃŽnh sau cÃģ nghiáŧm khÃīng tᚧm thÆ°áŧng.
- 73. GiÂķng viŠn: Phan §Ãļc TuÃn Äᚥi Sáŧ Tuyášŋn TÃnh â Äᚥi Sáŧ Tuyášŋn TÃnh â §5: Háŧ PTTT thuᚧn nhášĨt ïŪ Ta cÃģ 1 2 1 det( ) 2 1 3 1 1 A m â = â â â (3 6) 0m= + = 2mâ = â