Kinetic_Modeling_02_12_2016
- 1. MATLAB: soluzione di equazioni differenziali e fitting non lineare Focus principale sullŌĆÖutilizzo delle funzioni ode45 e lsqcurvefit Michele Scipioni Ph.D. Student Dip. Ingegneria dellŌĆÖinformazione Universit├Ā di Pisa Corso di Immagini Biomediche, 02 Dicembre 2016
- 2. 2 Outline ’āś PARTE 1 - Soluzione di un sistema di equazioni differenziali in MATLAB ’āś PARTE 2 - Fitting di modelli non lineari in MATLAB ’āś PARTE 3 - Esercitazione: implementazione e fitting di modelli bi-compartimentali A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
- 3. 3 PARTE 1 Soluzione di un sistema di equazioni differenziali in MATLAB A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
- 4. 4 Obiettivo A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare MODELLO BI-COMPARTIMENTALE DESCRITTO DA UN SISTEMA DI 2 EQUAZIONI DIFFERENZIALI 1. Prendere confidenza con le funzioni integrate in MATLAB dedicate alla soluzione delle ODE. 2. Impostare le opzioni e i parametri richiesti dal motore di soluzione ODE. 3. Passare il nostro modello ed eventuali parametri aggiuntivi al risolutore.
- 5. 5A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Risoluzione numerica di equazioni differenziali MATLAB fornisce un gran numero di strumenti per risolvere numericamente delle equazioni differenziali. Noi ci concentraremo sui due metodi principali gi├Ā integrati in tutte le versioni, ossia le funzioni ode23 e ode45, entrambe basate sul metodo di risoluzione Runge-Kutta. Entrambe queste funzioni si presentano con la medesima interfaccia e si aspettano gli stessi parametri in ingresso. ŌĆó y: vettore di soluzione, in cui ogni colonna ├© associata ad una variabile (pi├╣ di una se lavoriamo con un sistema di ODE), ed ogni riga rappresenta un istante temporale riferito al vettore t. ŌĆó odefun: funzione esterna (m-file) che restituisce un vettore colonna con IŌĆÖuscita del sistema ODE ŌĆó tspan: specifica il vettore dei tempi di integrazione per risolvere il Sistema ’é¦ se tspan ├© un vettore di due elementi, questi sono trattati come tempi di inizio e fine, e gli step di integrazione intermedi sono scelti arbitrariamente dal risolutore ’é¦ se tspan ha pi├╣ di 2 valori, i risultati sono calcolati soltanti per gli specifici istanti temporali richiesti ŌĆó y0: vettore delle condizioni iniziali per (t=0) [t, y] = ode45(odefun, tspan, y0)
- 6. 6A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: equazione differenziale del primo ordine ØææØæ” ØææØæź = ØæźØæ”2 + Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5] 1) Definire la funzione ØÉ©ØÉØØÉ×ØɤØÉ«Øɦ: ØÆć ØÆÖ, ØÆÜ = ØÆÜŌĆ▓
- 7. 7A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: equazione differenziale del primo ordine ØææØæ” ØææØæź = ØæźØæ”2 + Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5] 2) Passare la funzione appena creata in input al risolutore ode45()
- 8. 8A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: equazione differenziale del primo ordine ØææØæ” ØææØæź = ØæźØæ”2 + Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5] 3) Specificare un tspan personalizzato Quello che ├© interessante puntualizzare riguardo il tspan ├© che MATLAB in background continua ad usare pi├╣ o meno lo stesso timestep predefinito per risolvere lŌĆÖequazione differenziale, variando soltanto il modo in cui restituisce in output il risultato finale. Lavorare con un tspan personalizzato quindi non altera in modo eccessivo lŌĆÖaccuratezza della soluzione numerica.
- 9. 9A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: equazione differenziale del primo ordine ØææØæ” ØææØæź = ØæźØæ”2 + Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5] 4) Opzioni di personalizzazione Ad ogni iterazione del risolutore viene calcolato un errore. Se chiamiamo Øæ” Øæś lŌĆÖapprossimazione di Øæ” Øæź Øæś allo step k, ed ØæÆ Øæś lŌĆÖerrore corrispondente, MATLAB adatta il suo passo di integrazione in modo che risulti: ØÆå ØÆī Ōēż ØÆÄØÆéØÆÖ(Øæ╣ØÆåØÆŹØæ╗ØÆÉØÆŹ ŌłŚ |ØÆÜ ØÆī|, Øæ©ØÆāØÆöØæ╗ØÆÉØÆŹ), Dove i valori di default sono ØæģØæÆØæÖØæćØæ£ØæÖ = 10ŌłÆ3 = .001 and ØÉ┤ØæÅØæĀØæćØæ£ØæÖ = 10ŌłÆ6 = .000001. N.B. Con questa convenzione, se la soluzione |Øæ” Øæś| diventa molto grande, di conseguenza lo ├© anche lŌĆÖerrore, e per evitare che il risolutore si arresti prima di convergere ├© necessario ridurre RelTol. Viceversa, se la soluzione tende ad avere valori molto piccoli (< 10ŌłÆ6 ), allora ├© AbsTol a dover essere ridotto.
- 10. 10A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: equazione differenziale del primo ordine ØææØæ” ØææØæź = ØæźØæ”2 + Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5] 4) Opzioni di personalizzazione ØææØæ” ØææØæź = ØæźØæ”2 + Øæ”; Øæ” Øæź = 1 1 ŌłÆ Øæź
- 11. 11A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: sistemi di ODE Øø╝ = 1,2 Øæ”1 0 = 2 ØøĮ = ŌłÆ0,6 Øæ”2 0 = 1 Ø£Ä = ŌłÆ0,8 Ø£ī = 0,3 Modello Predator-Prey Vettore colonna 212 2 211 1 yyy dt dy yyy dt dy ’ü▓’ü│ ’üó’üĪ ’Ć½’ĆĮ ’ĆŁ’ĆĮ
- 12. 12A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: passaggio di parametri aggiuntivi Immaginiamo di voler continuare a lavorare allŌĆÖesempio del modello predatore-preda, ma variando il valore delle costanti del modello Øø╝, ØøĮ, Žā e Ø£ī, ma ovviamente senza modificare manualmente il file MATLAB.
- 13. 13 PARTE 2 Fitting di modelli non lineari in MATLAB A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
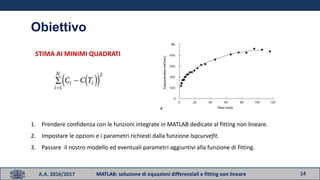
- 14. 14A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Obiettivo STIMA AI MINIMI QUADRATI 1. Prendere confidenza con le funzioni integrate in MATLAB dedicate al fitting non lineare. 2. Impostare le opzioni e i parametri richiesti dalla funzione lsqcurvefit. 3. Passare il nostro modello ed eventuali parametri aggiuntivi alla funzione di fitting.
- 15. 15A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Least Squares Estimator LŌĆÖobiettivo di uno stimatore ai minimi quadrati ├© trovare un vettore x che sia un minimizzatore locale della funzione data dalla somma degli scarti quadratici tra curva misurata e uscita del modello teorico, possibilmente sottoposta ad alcuni vincoli: ØæÜØæ¢Øæø Øæź ØÉ╣(Øæź) 2 2 = ØæÜØæ¢Øæø Øæź Øæ¢ ØÉ╣Øæ¢ 2 (Øæź) tale che ØÉ┤ ┬Ę Øæź Ōēż ØæÅ, ØÉ┤ØæÆØæ× ┬Ę Øæź = ØæÅØæÆØæ×, ØæÖØæÅ Ōēż Øæź Ōēż ØæóØæÅ.
- 16. 16A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare lsqcurvefit [x,resnorm,residual,exitflag,output] = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)INPUT ŌĆó ØÆćØÆ¢ØÆÅ(ØÆÖ, ØÆÖØÆģØÆéØÆĢØÆé): funzione non lineare che fornisce in output la stima della curva da fittare ’é¦ ØÆÖ: vettore dei parametri incogniti ’é¦ ØÆÖØÆģØÆéØÆĢØÆé: variabile indipendete (generalmente il vettore temporale a cui ├© campionato ydata) ŌĆó ØÆÖؤÄ: stima inziale dei coefficienti del modello da fittare ŌĆó ØÆÜØÆģØÆéØÆĢØÆé: curva misurata (deve essere della stessa misura dellŌĆÖoutput di fun) ŌĆó ØÆŹØÆā, ØÆ¢ØÆā: lower e upper bounds tali che ØæÖØæÅ Ōēż Øæź Ōēż ØæóØæÅ (devono avere stessa dimensione di x0, o essere matrici vuote se non si ├© interessati a vincolare la stima parametrica) ŌĆó ØÆÉØÆæØÆĢØÆŖØÆÉØÆÅØÆö: opzioni di ottimizzazione OUTPUT ŌĆó ØÆÖ: parametri del modello stimati (stessa dimensione di x0 e del vettore di parametri preso in input da fun(x,xdata)) ŌĆó ØÆōØÆåØÆöØÆÅØÆÉØÆōØÆÄ: somma degli scarti quadratici (residui) corrispondenti allŌĆÖoutput del fitting ŌĆó ØÆōØÆåØÆöØÆŖØÆģØÆ¢ØÆéØÆŹ: vettore dei residui [fun(x,xdata)-ydata] alla soluzione x ŌĆó ØÆåØÆÖØÆŖØÆĢØÆćØÆŹØÆéØÆł: valore che descrive la condizione di uscita ŌĆó ØÆÉØÆ¢ØÆĢØÆæØÆ¢ØÆĢ: struttura contenente informazioni riassuntive sul processo di ottimizzazione
- 17. 17A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: fitting di una funzione esponenziale Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2] 1) Definire la funzione ØÉ”ØÉ©ØÉØØÉ×ØÉźØÉźØÉ©: ØÆÜ = ØÆćØÆ¢ØÆÅ(ØÆÖ, ØÆÖØÆģØÆéØÆĢØÆé)
- 18. 18A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: fitting di una funzione esponenziale Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2] 2) Usiamo il modello implementato per simulare una misura rumorosa ydata
- 19. 19A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: fitting di una funzione esponenziale Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2] 3) Passare la funzione modello e il vettore misurato con input ad lsqcurvefit
- 20. 20A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: fitting di una funzione esponenziale Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2] 4) Passare parametri aggiuntivi alla funzione modello
- 21. 21A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Esempio: fitting di una funzione esponenziale Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2] 5) Principali opzioni per personalizzare il risultato del fitting x0 = [1 1 1 0] options = optimset('Display', 'none'); options.TolFun = 1e-6; options.TolX = 1e-6; options.MaxFunEvals = 1e6; options.MaxIter = 1e6; lb = [0. 5. 5. 0.]; ub = [5. 15. 10. 3.];
- 22. 22 PARTE 3 Esercitazione: implementazione e fitting di modelli bi-compartimentali ad un dataset PET A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Link per scaricare i dati sperimentali per lŌĆÖesercitazione
- 23. 23A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare Punti principali 1. Implementare modello bicompartimentale mediante ode45 2. Implementare modello bicompartimentale mediante la soluzione analitica bi-esponenziale 3. Verificare che i due modelli si comportano in modo analogo simulando delle curve usando i medesimi parametri cinetici 4. Estrarre una input function ed una curva tissutale dal dataset clinico fornito, e stimare i parametri cinetici usando entrambe le implementazioni del modello compartimentale 5. Usando lŌĆÖimplementazione pi├╣ veloce delle due, applicare il fitting a tutti i voxel dellŌĆÖimmagine, generando delle mappe parametriche ___________________________________ FACOLTATIVO: sfruttando lŌĆÖimplementazione dellŌĆÖalgoritmo ml-em sviluppato in una precedente esercitazione, cimentarsi nellŌĆÖimplementazione del metodo diretto di stima da sinogrammi, descritto nellŌĆÖultima parte della precedente lezione.
- 24. 24A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare 1. Implementare modello bicompartimentale mediante ode45 ØÉČ1 ØæĪ = 0 = ØÉŠ1 ØÉČ2 ØæĪ = 0 = 0 Consiglio: implementare due funzioni distinte nello stesso m-file function Ct = modello_ode(k, t) ’ā¤ funzione principale che calcola lŌĆÖuscita della ode45 e da in output Ct=C(:,1)+C(:,2); function Cp = sistema_ode(t,C,param) ’ā¤ funzione interna in cui vengono esplicitate le due equazioni differenziali del sistema
- 25. 25A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare 2. Implementare modello bicompartimentale mediante la soluzione analitica bi-esponenziale Øæ¬ Øæ╗ = Ø£Č Ø¤Å ØÆåŌłÆØ£Ę Ø¤Å ØÆĢ + Ø£Č Ø¤É ØÆåŌłÆØ£Ę Ø¤É ØÆĢ Øø╝1 = ØÉŠ1 Øæś3 + Øæś4 ŌłÆ ØøĮ1 ØøĮ2 ŌłÆ ØøĮ1 Øø╝2 = ØÉŠ1 ØøĮ2 ŌłÆ Øæś3 ŌłÆ Øæś4 ØøĮ2 ŌłÆ ØøĮ1 ØøĮ1 = Øæś2 + Øæś3 + Øæś4 ŌłÆ Øæś2 + Øæś3 + Øæś4 2 ŌłÆ 4Øæś2 Øæś4 2 ØøĮ2 = Øæś2 + Øæś3 + Øæś4 + Øæś2 + Øæś3 + Øæś4 2 ŌłÆ 4Øæś2 Øæś4 2 function Ct = modello_exp(k, time) Questa funzione deve prendere gli stessi ingressi della precedente (le 4 costanti del modello compartimentale e il vettore dei tempi) e svolgere al suo interno la conversione nel set di variabili ausiliarie prima di calcolare Øæ¬ Øæ╗(t).
- 26. 26A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare 3. Verificare che i due modelli si comportano in modo analogo Simulare le risposte impulsive (IRF) dei due tessuti con i seguenti valori di ingresso: ØæĪ = 0: 35; % Øæ¢Øæø ØæÜØæ¢ØæøØæóØæĪØæ¢ Øæś = [0.3 0.5 0.6 0.1];
- 27. 27A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare 4. Stimare i parametri cinetici dai dati sperimentali (1/2) 1. Importare il dataset allegato allŌĆÖesercitazione 2. Estrarre 2 curve tempo-attivit├Ā dalla matrice 4D ŌĆ£VolumeŌĆØ ŌĆó ROI Input function: slice 7, time frame 4 ŌĆó ROI tessuto: slice 23, time frame 24 3. Importare dalla struttura ŌĆ£PETInfoŌĆØ il vettore dei tempi: ŌĆó time = mean(PETInfo.time,2)./60; 4. Implementare le formule riportate nella diapositiva 33 della lezione precedente utilizzando la funzione riportata nella prossima slide. Usare questŌĆÖultima come ingresso allŌĆÖalgoritmo di ottimizzazione lsqcurvefit 5. Impostare le seguenti opzioni di ottimizzazione: ŌĆó lb = [ 0. 0. 0. 0. 0. ]; % K1 k2 k3 k4 vB ŌĆó ub= [ 1. 1. 1. 1. 1. ]; % K1 k2 k3 k4 vB ŌĆó k0= [ 0.1 0.1 0.01 0.01 0.1]; % K1 k2 k3 k4 vB
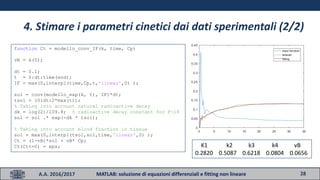
- 28. 28A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare function Ct = modello_conv_IF(k, time, Cp) vB = k(5); dt = 0.1; t = 0:dt:time(end); IF = max(0,interp1(time,Cp,t,'linear',0) ); sol = conv(modello_exp(k, t), IF)*dt; tsol = (0:dt:2*max(t)); % Taking into account natural radioactive decay dk = log(2)/109.8; % radioactive decay constant for F-18 sol = sol .* exp(-dk * tsol); % Taking into account blood fraction in tissue sol = max(0,interp1(tsol,sol,time,'linear',0) ); Ct = (1-vB)*sol + vB* Cp; Ct(Ct<=0) = eps; K1 k2 k3 k4 vB 0.2820 0.5087 0.6218 0.0804 0.0656 4. Stimare i parametri cinetici dai dati sperimentali (2/2)
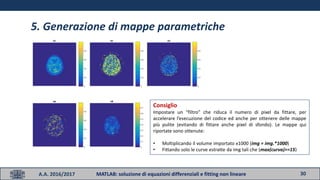
- 29. 29A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare 5. Generazione di mappe parametriche 1. Importare il dataset allegato allŌĆÖesercitazione 2. Estrarre 1 curva tempo-attivit├Ā dalla matrice 4D ŌĆ£VolumeŌĆØ relativa alla input function (ROI da slice 7, time frame 4) 3. Importare dalla struttura ŌĆ£PETInfoŌĆØ il vettore dei tempi: ŌĆó time = mean(PETInfo.time,2)./60; 4. Scegliere una fetta del volume PET importato (ad esempio la 24 da cui si ├© estratta la ROI precedente o qualsiasi altra a piacere) e fittare voxel per voxel il modello, come fatto al punto precedente. ŌĆó img = squeeze(Volume(:,:,24,:));
- 30. 30A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare 5. Generazione di mappe parametriche Consiglio Impostare un ŌĆ£filtroŌĆØ che riduca il numero di pixel da fittare, per accelerare lŌĆÖesecuzione del codice ed anche per ottenere delle mappe pi├╣ pulite (evitando di fittare anche pixel di sfondo). Le mappe qui riportate sono ottenute: ŌĆó Moltiplicando il volume importato x1000 (img = img.*1000) ŌĆó Fittando solo le curve estratte da img tali che (max(curva)>=15)
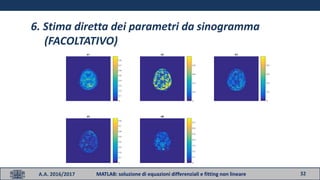
- 31. 31A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare 6. Stima diretta dei parametri da sinogramma (FACOLTATIVO) 1. Importare il dataset allegato allŌĆÖesercitazione 2. Estrarre 1 curve tempo-attivit├Ā dalla matrice 4D ŌĆ£VolumeŌĆØ relativa all input function (slice 7, time frame 4) 3. Importare dalla struttura ŌĆ£PETInfoŌĆØ il vettore dei tempi: ŌĆó time = mean(PETInfo.time,2)./60; 4. Scegliere una fetta del volume PET importato (ad esempio la 24 da cui si ├© estratta la ROI precedente o qualsiasi altra a piacere) e fittare voxel per voxel il modello, come fatto al punto precedente. 5. Richiamare lŌĆÖesercitazione sullŌĆÖalgoritmo di ricostruzione MLEM (28 Ottobre 2016) e: ŌĆó utilizzare la matrice di sistema (A) per convertire il volume PET in un sinogramma dinamico (come fatto con il fantoccio lŌĆÖaltra volta) ŌĆó ŌĆ£copiareŌĆØ il blocco di codice che esegue 1 iterazione di MLEM, facendo lŌĆÖipotesi che il sinogramma non abbia artefatti da correggere 6. Implementare il metodo diretto di stima parametrica, alternando una iterazione MLEM ad un fitting dellŌĆÖintero volume ricostruito, come svolto al punto 5.
- 32. 32A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare 6. Stima diretta dei parametri da sinogramma (FACOLTATIVO)





![5A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Risoluzione numerica di equazioni differenziali
MATLAB fornisce un gran numero di strumenti per risolvere numericamente delle equazioni differenziali.
Noi ci concentraremo sui due metodi principali gi├Ā integrati in tutte le versioni, ossia le funzioni ode23 e
ode45, entrambe basate sul metodo di risoluzione Runge-Kutta.
Entrambe queste funzioni si presentano con la medesima interfaccia e si aspettano gli stessi parametri
in ingresso.
ŌĆó y: vettore di soluzione, in cui ogni colonna ├© associata ad una variabile (pi├╣ di una se lavoriamo con
un sistema di ODE), ed ogni riga rappresenta un istante temporale riferito al vettore t.
ŌĆó odefun: funzione esterna (m-file) che restituisce un vettore colonna con IŌĆÖuscita del sistema ODE
ŌĆó tspan: specifica il vettore dei tempi di integrazione per risolvere il Sistema
’é¦ se tspan ├© un vettore di due elementi, questi sono trattati come tempi di inizio e fine, e gli
step di integrazione intermedi sono scelti arbitrariamente dal risolutore
’é¦ se tspan ha pi├╣ di 2 valori, i risultati sono calcolati soltanti per gli specifici istanti temporali
richiesti
ŌĆó y0: vettore delle condizioni iniziali per (t=0)
[t, y] = ode45(odefun, tspan, y0)](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-5-320.jpg)
![6A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: equazione differenziale del primo ordine
ØææØæ”
ØææØæź
= ØæźØæ”2
+ Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5]
1) Definire la funzione ØÉ©ØÉØØÉ×ØɤØÉ«Øɦ: ØÆć ØÆÖ, ØÆÜ = ØÆÜŌĆ▓](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-6-320.jpg)
![7A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: equazione differenziale del primo ordine
ØææØæ”
ØææØæź
= ØæźØæ”2
+ Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5]
2) Passare la funzione appena creata in input al risolutore ode45()](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-7-320.jpg)
![8A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: equazione differenziale del primo ordine
ØææØæ”
ØææØæź
= ØæźØæ”2
+ Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5]
3) Specificare un tspan personalizzato
Quello che ├© interessante puntualizzare riguardo il
tspan ├© che MATLAB in background continua ad
usare pi├╣ o meno lo stesso timestep predefinito
per risolvere lŌĆÖequazione differenziale, variando
soltanto il modo in cui restituisce in output il
risultato finale. Lavorare con un tspan
personalizzato quindi non altera in modo eccessivo
lŌĆÖaccuratezza della soluzione numerica.](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-8-320.jpg)
![9A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: equazione differenziale del primo ordine
ØææØæ”
ØææØæź
= ØæźØæ”2
+ Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5]
4) Opzioni di personalizzazione
Ad ogni iterazione del risolutore viene calcolato un errore. Se chiamiamo Øæ” Øæś lŌĆÖapprossimazione di
Øæ” Øæź Øæś allo step k, ed ØæÆ Øæś lŌĆÖerrore corrispondente, MATLAB adatta il suo passo di integrazione in
modo che risulti:
ØÆå ØÆī Ōēż ØÆÄØÆéØÆÖ(Øæ╣ØÆåØÆŹØæ╗ØÆÉØÆŹ ŌłŚ |ØÆÜ ØÆī|, Øæ©ØÆāØÆöØæ╗ØÆÉØÆŹ),
Dove i valori di default sono ØæģØæÆØæÖØæćØæ£ØæÖ = 10ŌłÆ3
= .001 and ØÉ┤ØæÅØæĀØæćØæ£ØæÖ = 10ŌłÆ6
= .000001.
N.B.
Con questa convenzione, se la soluzione |Øæ” Øæś| diventa molto grande, di conseguenza lo ├© anche lŌĆÖerrore, e per
evitare che il risolutore si arresti prima di convergere ├© necessario ridurre RelTol. Viceversa, se la soluzione
tende ad avere valori molto piccoli (< 10ŌłÆ6
), allora ├© AbsTol a dover essere ridotto.](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-9-320.jpg)
![10A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: equazione differenziale del primo ordine
ØææØæ”
ØææØæź
= ØæźØæ”2
+ Øæ”; Øæ” 0 = 1 Øæź Ōłł [0; 0.5]
4) Opzioni di personalizzazione
ØææØæ”
ØææØæź
= ØæźØæ”2
+ Øæ”; Øæ” Øæź =
1
1 ŌłÆ Øæź](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-10-320.jpg)




![16A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
lsqcurvefit
[x,resnorm,residual,exitflag,output] =
lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)INPUT
ŌĆó ØÆćØÆ¢ØÆÅ(ØÆÖ, ØÆÖØÆģØÆéØÆĢØÆé): funzione non lineare che fornisce in output la stima della curva da fittare
’é¦ ØÆÖ: vettore dei parametri incogniti
’é¦ ØÆÖØÆģØÆéØÆĢØÆé: variabile indipendete (generalmente il vettore temporale a cui ├© campionato ydata)
ŌĆó ØÆÖؤÄ: stima inziale dei coefficienti del modello da fittare
ŌĆó ØÆÜØÆģØÆéØÆĢØÆé: curva misurata (deve essere della stessa misura dellŌĆÖoutput di fun)
ŌĆó ØÆŹØÆā, ØÆ¢ØÆā: lower e upper bounds tali che ØæÖØæÅ Ōēż Øæź Ōēż ØæóØæÅ (devono avere stessa dimensione di x0, o essere matrici vuote se
non si ├© interessati a vincolare la stima parametrica)
ŌĆó ØÆÉØÆæØÆĢØÆŖØÆÉØÆÅØÆö: opzioni di ottimizzazione
OUTPUT
ŌĆó ØÆÖ: parametri del modello stimati (stessa dimensione di x0 e del vettore di parametri preso in input da fun(x,xdata))
ŌĆó ØÆōØÆåØÆöØÆÅØÆÉØÆōØÆÄ: somma degli scarti quadratici (residui) corrispondenti allŌĆÖoutput del fitting
ŌĆó ØÆōØÆåØÆöØÆŖØÆģØÆ¢ØÆéØÆŹ: vettore dei residui [fun(x,xdata)-ydata] alla soluzione x
ŌĆó ØÆåØÆÖØÆŖØÆĢØÆćØÆŹØÆéØÆł: valore che descrive la condizione di uscita
ŌĆó ØÆÉØÆ¢ØÆĢØÆæØÆ¢ØÆĢ: struttura contenente informazioni riassuntive sul processo di ottimizzazione](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-16-320.jpg)
![17A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: fitting di una funzione esponenziale
Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2]
1) Definire la funzione ØÉ”ØÉ©ØÉØØÉ×ØÉźØÉźØÉ©: ØÆÜ = ØÆćØÆ¢ØÆÅ(ØÆÖ, ØÆÖØÆģØÆéØÆĢØÆé)](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-17-320.jpg)
![18A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: fitting di una funzione esponenziale
Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2]
2) Usiamo il modello implementato per simulare una misura rumorosa ydata](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-18-320.jpg)
![19A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: fitting di una funzione esponenziale
Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2]
3) Passare la funzione modello e il vettore misurato con input ad lsqcurvefit](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-19-320.jpg)
![20A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: fitting di una funzione esponenziale
Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2]
4) Passare parametri aggiuntivi alla funzione modello](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-20-320.jpg)
![21A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
Esempio: fitting di una funzione esponenziale
Øæ” = ØæÄ1 exp ŌłÆØæÅ1 ØæĪ + ØæÄ2 exp ŌłÆØæÅ2 ØæĪ ØæĪ Ōłł [0; 2]
5) Principali opzioni per personalizzare il risultato del fitting
x0 = [1 1 1 0]
options = optimset('Display', 'none');
options.TolFun = 1e-6;
options.TolX = 1e-6;
options.MaxFunEvals = 1e6;
options.MaxIter = 1e6;
lb = [0. 5. 5. 0.];
ub = [5. 15. 10. 3.];](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-21-320.jpg)




![26A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
3. Verificare che i due modelli si comportano in
modo analogo
Simulare le risposte impulsive (IRF) dei
due tessuti con i seguenti valori di
ingresso:
ØæĪ = 0: 35; % Øæ¢Øæø ØæÜØæ¢ØæøØæóØæĪØæ¢
Øæś = [0.3 0.5 0.6 0.1];](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-26-320.jpg)
![27A.A. 2016/2017 MATLAB: soluzione di equazioni differenziali e fitting non lineare
4. Stimare i parametri cinetici dai dati sperimentali (1/2)
1. Importare il dataset allegato allŌĆÖesercitazione
2. Estrarre 2 curve tempo-attivit├Ā dalla matrice 4D ŌĆ£VolumeŌĆØ
ŌĆó ROI Input function: slice 7, time frame 4
ŌĆó ROI tessuto: slice 23, time frame 24
3. Importare dalla struttura ŌĆ£PETInfoŌĆØ il vettore dei tempi:
ŌĆó time = mean(PETInfo.time,2)./60;
4. Implementare le formule riportate nella diapositiva 33 della lezione precedente
utilizzando la funzione riportata nella prossima slide. Usare questŌĆÖultima come
ingresso allŌĆÖalgoritmo di ottimizzazione lsqcurvefit
5. Impostare le seguenti opzioni di ottimizzazione:
ŌĆó lb = [ 0. 0. 0. 0. 0. ]; % K1 k2 k3 k4 vB
ŌĆó ub= [ 1. 1. 1. 1. 1. ]; % K1 k2 k3 k4 vB
ŌĆó k0= [ 0.1 0.1 0.01 0.01 0.1]; % K1 k2 k3 k4 vB](https://image.slidesharecdn.com/6f716576-d9ff-4052-a5f6-83b0bf75a276-161215093051/85/Kinetic_Modeling_02_12_2016-27-320.jpg)