狠狠撸

サンプルで学ぶ础濒濒辞测

はじめに
? 本資料は2010年頃，Analyzer 4.1.10とかが出
てた頃に作成した資料で，ちょっと古い内容が
含まれてるかもしれません．
一応URLとかは最近(2014年12月)に一通りチェックはしたつもりですが．．．
? 本資料（特にサンプル）には誤りを含んでいる
かもしれません．お気づきの場合はご連絡いた
だけると幸いです．
– 厳密には実際に試していただくか，参考文献を参照
して下さい．
– サンプルなどはあくまでも一例です．
? 説明を聞くよりも，実際にやっていただきなが
ら，特徴をつかんでいただければ．

Alloyとは
? モデリング言語及び解析ツールの名称
– MIT のDaniel Jackson 氏を中心に開発され，1997
年にプロトタイプ公開．
? 一階の関係論理(relational logic)をベースにし
ている
Alloy言語= 一階論理+関係代数+推移閉包
? 宣言的(declarative)に記述されたモデルの事例
及び反例を自動的に検出する

参考
? ホームページ
http://alloy.mit.edu/alloy/
? 文献
– [1]Daniel Jackson ，Software Abstractions: Logic,
Language, and Analysis
自分が参照したのは2006年発刊の旧版で，今は新版が出てます
– [2]中島, 鵜林, Alloy:自動解析可能なモデル規範形式仕
様言語，コンピュータソフトウェアVol. 26 (2009),
No.3
– [3]藤倉, Alloyによるモデリング, Interface 2009年12
月号
今ではもっといろいろあると思います．．．

検証のしくみ
? 関係論理に基づくAlloyモデルをkodkod でコン
パイルしてCNF(乗法標準形)に変換し，
SAT(satisfiability)ソルバで解く
? Kodkod
– http://alloy.mit.edu/kodkod/
? SAT solver(様々なものがあり，下記はその1つ)
– http://www.sat4j.org/

Alloyによる検証の考え方
? システムの正しさを完全に証明する能力を犠牲
にし，限られた範囲でシステムの制約を破るよ
うな反例を見つけることを目指す．
? small scope hypothesis
– Most bugs have small counterexamples
? 「大抵のバグは小さな反例をもつ」
? 文献[2]では有限スコープ仮説と呼んでいる
? scope monotonicity
– もしある制約があるスコープでインスタンスを持つ
ならば，より大きなスコープにおいても同様にイン
スタンスを持つ

用語定義(1)
? アトム(Atom)
– それ以上分割できない最小の構成要素
? Alloy のモデルで直接アトムを記述することはない
? 関係(relation)
– 数学：順序対の集合．直積の部分集合．
? a≠b ならば(a,b)≠(b,a)
? (a,b)=(c,d) ? a=c かつb=d
(例) A={赤,青,黄}, B={大,小} としたとき
R = {(赤,小), (青,大)} ? A×B は一つの関係
– 様々な関係を表現するのに使う
? …が～を構成要素としてもつ
? …が～という値(状態)にある
? …の次は～である
– Alloy のモデルでは，すべてのものを関係として扱う

用語定義(2)
? (関係の)アリティ(arity)
– 一つの順序対に含まれる要素の数
? それが1,2,3のときそれぞれ単項関係(unary relation),2
項関係(binary relation), 3項関係(ternary relation)
? (関係の)サイズ(size)
– 関係の要素である順序対の数
( B0, N0, D0 )
( B0, N1, D1 )
( B1, N1, D2 )
( B1, N2, D2 )
arity = 3 （順序対の要素数）
size = 4
（順序対の数）

用語定義(3)
? 様々な要素が関係を用いて再定義される
? (アトムの)集合
– arity が１の関係(つまり，unary relation)
Name = {(N0), (N1), (N2)}
? スカラー（scalar）
– size, arity が共に１の関係
myName = {(N0)}
– Alloyではa, {a}, (a), {(a)} は同じ扱い．
? 関係が空(empty)
– 組(tuple)の存在しない関係(size = 0)
? オプション
– 空またはスカラーのいずれかとなる関係
– “size = 0 or 1” の“unary relation”

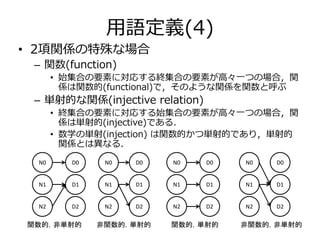
用語定義(4)
? 2項関係の特殊な場合
– 関数(function)
? 始集合の要素に対応する終集合の要素が高々一つの場合，関
係は関数的(functional)で，そのような関係を関数と呼ぶ
– 単射的な関係(injective relation)
? 終集合の要素に対応する始集合の要素が高々一つの場合，関
係は単射的(injective)である．
? 数学の単射(injection) は関数的かつ単射的であり，単射的
関係とは異なる．
N0
N1
N2
D0
D1
D2
N0
N1
N2
D0
D1
D2
N0
N1
N2
D0
D1
D2
N0
N1
N2
D0
D1
D2
関数的，非単射的非関数的，単射的関数的，単射的非関数的，非単射的

用語定義(5)
? (関係の)定義域(domain)
– 関係の各要素(組)の第一要素だけを取り出した組の集
合(unary relation)
? 値域(range)
– 関係の各要素(組)の最終要素だけを取り出した組の集
合(unary relation)
? 例
addr={(B0,N0,D0), (B0,N1,D1), (B1,N2,D2)}
addr の定義域= {(B0),(B1)}
addr の地域= {(D0),(D2)}

Alloyモデルの主な構文要素
? open 名前
– 他のモジュールを呼び出す
? module 名前
– モジュール名を宣言する
? sig 名前{関係の宣言}{制約}
– アトムの集合およびその集合を定義域とする関係を表現する
? fact {制約}
– システム全体で満たすべき制約を表現する
? pred 名前{制約}
– 論理式(formula)を表現する
? fun 名前[引数宣言]: 戻り値の型{式}
– 式(expression)を表現する
? run 名前スコープ，または，run {制約} スコープ
– 指定したスコープで，指定した制約を満たす事例を生成する．
? assert 名前{制約}
– check で反例をチェックしたい条件を記述する
? check 名前スコープ，または， check {制約} スコープ
– 指定したassert に対する反例を生成する

実际に试してみましょう

ツールの入手，起動
? ダウンロード
http://alloy.mit.edu/alloy/download.html
– Eclipse プラグインもあります(必須ではない)
http://code.google.com/p/alloy4eclipse/
今でも使えるのか，ちょっと確認してないです
? 実行方法
– alloy4.jar ダウンロード後，ファイルをダブルクリッ
クまたはコマンドラインから実行
java –jar alloy4.jar

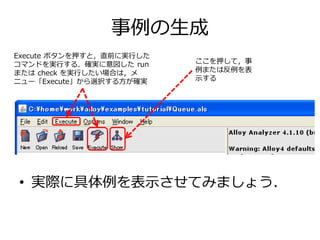
事例の生成
Execute ボタンを押すと，直前に実行した
コマンドを実行する．確実に意図したrun
またはcheck を実行したい場合は，メ
ニュー「Execute」から選択する方が確実
ここを押して，事
例または反例を表
示する
? 実際に具体例を表示させてみましょう．

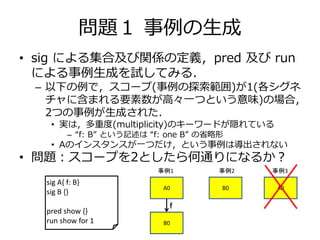
問題１事例の生成
? sig による集合及び関係の定義，pred 及びrun
による事例生成を試してみる．
– 以下の例で，スコープ(事例の探索範囲)が1(各シグネ
チャに含まれる要素数が高々一つという意味)の場合，
2つの事例が生成された．
? 実は，多重度(multiplicity)のキーワードが隠れている
– “f: B” という記述は“f: one B” の省略形
? Aのインスタンスが一つだけ，という事例は導出されない
? 問題：スコープを2としたら何通りになるか？
sig A{ f: B}
sig B {}
pred show {}
run show for 1
事例1 事例2
A0
B0
B0
ｆ
事例3
A0

答え：７通り
A
B
B
ｆ
対象にしない
A
B1
ｆ
B0
B1 B0
A1
B1
ｆ
A0
B0
ｆ
A1
B
ｆ
A0
ｆ
A0
B1
ｆ
A1
B0
ｆ
A0個，B0個A0個，B1個A0個，B2個
あり得ない

アトムの性質
? 同じシグネチャに含まれるアトムは区別されな
い
– 下図のような事例は区別されない
? 区別したい場合，アトムの集合を部分集合に分
割する
A
B1
ｆ
B0
A
B1
ｆ
B0
同じ事例

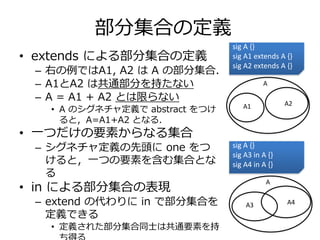
部分集合の定義
? extends による部分集合の定義
– 右の例ではA1, A2 はA の部分集合．
– A1とA2 は共通部分を持たない
– A = A1 + A2 とは限らない
? A のシグネチャ定義でabstract をつけ
ると，A=A1+A2 となる．
? 一つだけの要素からなる集合
– シグネチャ定義の先頭にone をつ
けると，一つの要素を含む集合とな
る
? in による部分集合の表現
– extend の代わりにin で部分集合を
定義できる
? 定義された部分集合同士は共通要素を持
ち得る
sig A {}
sig A1 extends A {}
sig A2 extends A {}
A
A1 A2
sig A {}
sig A3 in A {}
sig A4 in A {}
A
A3 A4

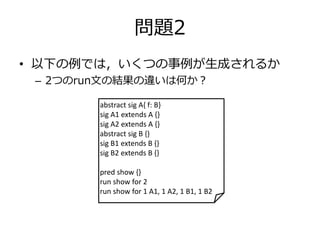
問題2
? 以下の例では，いくつの事例が生成されるか
– 2つのrun文の結果の違いは何か？
abstract sig A{ f: B}
sig A1 extends A {}
sig A2 extends A {}
abstract sig B {}
sig B1 extends B {}
sig B2 extends B {}
pred show {}
run show for 2
run show for 1 A1, 1 A2, 1 B1, 1 B2

特殊な関係
? 空の関係none
– 数学的には空集合{} を意味する
? 全集合(universal set) univ
– すべてのアトムを含む集合
– シグネチャとして定義された集合はuniv をextend
したものであると考えることができる．
? 恒等関係(identity) iden
– すべてのアトムが自分自身と関係する2項関係
? 例
システムに存在する全てのアトムが
Name={(N0),(N1),(N2)}, Addr={(D0),(D1)}
のとき，次のようになる．
none = {}
univ={(N0),(N1),(N2),(D0),(D1)}
iden={(N0,N0),(N1,N1),(N2,N2),(D0,D0),(D1,D1)}

新たな関係を作るための演算子
? 集合操作
p+q 合併(union)
p&q 共通部分(intersection)
p-q 差(difference)
? 関係操作
p->q 直積(product)
p.q 結合(join)※後述, p.q はq[p] とも記述できる
? a.b.c[d] は，d.(a.b.c) に等しい
~p 転置(transpose)
? 2項関係p の要素の順番を入れ替えたもの
^p 推移的閉包(transitive closure)※後述
*p 反射的推移的閉包(reflexive-transitive closure)
*p = ^p + iden
s<:r 定義域制限(domain restriction)
r:>s 値域制限(range restriction)
p++q 割り込み，上書き(override)
? 存在しない場合は追加し，存在する場合は上書きする

関係の結合
? 関係の合成を行う
to = {(M0,N0), (M0,N2), (M1,N2), (M2,N3)}
addr = {(N0,D0), (N0,D1), (N1,D1), (N1,D2),
(N2,D3), (N4,D3,)}
のとき，
to.address = {(M0,D0), (M0,D1), (M1,D3),
(M0,D3)}
M0
N0
D0
M1
M2
N1
N2
N3
N4
D1
D2
D3

推移的閉包(1)
? 次のとき，関係r は推移的である．
– (a,b) 及び(b,c) が関係に含まれるとき，常に(a,c)
が関係に含まれる
? 例）r == {(a,d), (c,d), (d,b), (e,a)}
– この場合，r は推移的でない
? (a,d), (d,b) を含むが(a,b) を含まない
? (c,d), (d,b) を含むが(c,b) を含まない
? (e,a), (a,d) を含むが(e,d) を含まない．

推移的閉包(2)
? 関係r の閉包
– r を部分集合としてもち，かつ，ある性質（反射的，
推移的など）を持つような最小の関係
? r の推移的閉包^r は次のようになる
^r= {(e,a), (e,d), (e,b), (a,d), (a,b), (c,d), (c,b),
(d,b)}
e a d b
c

内包的定義による関係
? 書式
{x1:e1, x2:e2 , .. , xn:en | F}
– F という制約を満たす，x1-> x2->... -> xn という型
の関係
? 例
– Name という集合の要素n 及びAddr という集合の
要素a の組で，関係address に含まれているものの
集合(結果はName->Address の部分集合)
– {n: Name, a: Addr | n->a in address}

多重度(multiplicity)
? 要素の個数に関する制約を表現するためのもの
– set 任意の数
– one ちょうど１
– lone ０または１
– some １以上
? 暗黙の多重度
– 宣言における“x: e” は，”x: one e” に等しい

関係の多重度
? 一般形式r: A m -> n B
– 読み方：「Aの各メンバはBのnメンバに対応し，Bの
各メンバはAのmメンバに対応する」
– 次の意味に等しい
? all a: A | n a.r
? all b: B | m r.b
r: A -> one B A を定義域とする(全)関数
r: A -> lone B 定義域がAの部分関数
r: A one -> B 値域がBの単射的関係
r: A one -> one B 全単射(bijection)
r: A some -> some B 定義域がA,値域がBの関係
r: A lone -> some B Aの各メンバに一つ以上のBのメンバが対応し，Bの各メンバ
に高々一つのAのメンバが対応する
?A -> B で置き換え可能

制約表現のためのキーワード
集合間の関係
P in Q P はQ の部分集合である
P = Q P とQ は(集合が)等しい
論理演算子
not ! ???ではない(否定, negation)
P and Q P && Q P かつQ (合接, conjunction)
P or Q P || Q P またはQ , (離接, disjunction)
P implies
Q [else R]
P => Q else R PならばQ ,PでなければR (含意, implication, 代替,
alternative)
P iff Q P <=> Q P ならばQ かつQ ならばP (両含意, bi-implication)
量化(quantifier)
all すべての
some 存在する
no ない
lone 高々一つ
one 厳密に一つ

集合の濃度(Cardinality)
? 関係に#を適用すると，集合の濃度(要素の個
数)を意味する
– 濃度は整数値として扱われる
? 利用可能な演算子
+, -, =, <, >, =<, >=

記述を楽にするための記法
? let というキーワードを利用して，繰り返し使われ
る表現や長く複雑な表現を簡略化する
? 例
all a: Alias | let w=a.workAddress |
a.address = if some w then w else a.homeAddress

記号の優先順位
~ * ^
.
[]
:>
<:
->
&
++
#X
+ -
<< >> >>>
no X some X lone X one X set X seq X
in = < > <= >= !in != !< !> !<= !>=
!
&&
=> => Else
<=>
||
let all a:X|F no a:X|F some a:X|F lone a:X|F one a:x|F sum a:x|F
優先順位高
優先順位低

問題3 推理パズル
? 5人は最近の行事について話しています．以下の
話からそれぞれの参加した行事と，その前に買っ
たものを推理してください．
別にAlloy使わなくても解けるんですけど，練習ということで
? 参加した行事と買ったものはそれぞれ異なり，表
（元記事には表が示されている）の中のどれかに
該当します．
? 卒業式に行った人が買ったものは何でしょう？
（朝日新聞2010年4月3日土曜版「beパズル」より）
? 行事及び買ったものの候補：
– 行事：卒業式，海外旅行，入社式，花見，ハイキング
– 買ったもの：靴，ハンカチ，シャツ，ズボン，カメラ

5人の話
1. 田中：
– 私はシャツを買いました．
2. 竹内：
– 私は花見に行く前にズボンを買いました．
3. 石田：
– 私ではありませんが，入社式に行った人は靴を買った
そうです．
4. 葛西：
– 私も田中さんも卒業式には行っていません．
5. 青山：
– 私が行ったのは卒業式でもハイキングでもありません．
– 買ったのは靴でもカメラでもありません．
? 5人の話をfact として記述してみる．

行事及び買ったもの
abstract sig Event {}
one sig GraduationCeremony extends Event {} // 卒業式
one sig TravelingAbroad extends Event {} // 海外旅行
one sig InitiationCeremony extends Event {} // 入社式
one sig FlowerViewing extends Event {} // 花見
one sig Hiking extends Event {} // ハイキング
abstract sig Item {}
one sig Shoes extends Item {} // 靴
one sig Handkerchief extends Item {} // ハンカチ
one sig Shirt extends Item {} // シャツ
one sig Slacks extends Item {} // ズボン
one sig Camera extends Item {} // カメラ

人
abstract sig Person {
event: Event,
item: Item
}
one sig Tanaka extends Person {}
one sig Takeuchi extends Person {}
one sig Ishida extends Person {}
one sig Kasai extends Person {}
one sig Aoyama extends Person {}
// 参加した人は皆，一つの行事に参加し，一つのものを買っている．
// 参加した行事と買ったものはそれぞれ異なる．
fact {
all p1, p2: Person | p1=p2 implies p1.event = p2.event else p1.event != p2.event
all p1, p2: Person | p1=p2 implies p1.item = p2.item else p1.item != p2.item
}

fact による制約記述と事例解析
// 田中さん「私はシャツを買いました」
fact {
Tanaka.item in Shirt
}
// 竹内さん「私は花見に行く前にズボンを買いました」
fact {
Takeuchi.item in Slacks
Takeuchi.event in FlowerViewing
}
// 石田さん「私ではありませんが，入社式に行った人は靴を買ったそうです」
fact {
all p:Person | p.event in InitiationCeremony implies p.item in Shoes
Ishida.item not in Shoes
Ishida.event not in InitiationCeremony
}
// 残りの話は省略（課題）
pred show {}
run show

問題4 スケジュール調整
? ある組織は６日間の企業向け研修コースを実施
している．
? ６日間の研修はそれぞれメイン，サブとして２
人が担当する．
? 組織には3人の職員S, W, O がいて，担当日数
の差は高々一日になるように割り振りたい．
? ただし，１日目のメインはO，２日目のメイン
はW, ３日目のメインはS が担当することに決
まっている．
? メイン担当は次の日に何も担当しない．
? どのような割り振りがあるか．4日コースでは？

担当日，担当者
// 順序関係を表現するためのライブラリを利用
open util/ordering[Day]
// 担当日．メインとサブがいる．
sig Day {
main : Person,
sub: Person
}
// 担当者．メインとなる日とサブとなる日がある．
abstract sig Person {
mainDays : set Day,
subDays: set Day
}
// それぞれの職員．
one sig PersonS extends Person {}
one sig PersonO extends Person {}
one sig PersonW extends Person {}

ルール
// いろんなルール
fact {
// メインを担当する人とサブを担当する人が等しくなる日はない
no d: Day | d.main = d.sub
// すべての人は，メインとなる日にサブに割り当てられることはない
all d: Day, p: Person | d in p.mainDays implies d not in p.subDays
// dのメインがpならpのメイン担当日にdは入っている，そうじゃなければ入ってない
all d: Day, p: Person |
p in d.main implies d in p.mainDays else d not in p.mainDays
// dのサブがpならpのサブ担当日にdは入っている，そうじゃなければ入ってない
all d: Day, p: Person |
p in d.sub implies d in p.subDays else d not in p.subDays
// dのメイン担当者がpならpはdのサブ担当者ではない
all d: Day, p: Person | p in d.main implies p not in d.sub
}
// すべての人の担当日数の差は1日以内
fact {
all p1, p2: Person | #p1.(mainDays+subDays) - #p2.(mainDays+subDays) =< 1
}

ルール
// 一日目のメインはO が担当
// 二日目のメインはW が担当
// 三日目のメインはS が担当
fact {
first.main in PersonO
first.next.main in PersonW
first.next.next.main in PersonS
}
// 続けて２日間メインを担当しない
fact {
all d: (Day-last) | d.main not in (d.next.main+d.next.sub)
}

事例チェック
// 事例の解析（6日間のコースの場合）
run {} for 3 but 6 Day
// 事例の解析（4日間のコースの場合）
run {} for 3 but 4 Day
// 日付と担当者の関係は，担当者と日付の関係に等しい
// 図を見ればそれらしいことがわかるが，
// すべての場合でそうなるかを確認．
assert mainEqualmainDay{
~mainDays = main
~subDays = sub
}
check mainEqualmainDay for 3 but 6 Day

問題5：信号機
※参考文献[1]から抜粋
? (高速道路などの）合流点（ジャンクション）と
信号機があり，合流点にはいくつかの信号機が
設置されている
? 各信号機は，赤?青?黄のいずれかを表示する．
? 合流点の信号機は次の制約を満たす．
1. 同じ合流点内に赤でない信号機は高々一つしか存在
しない
2. すべての信号機は正しい順序で色が変化する
3. 同時には高々一つの信号機のみ色が変化する
4. ある信号機が赤から赤以外へ変化する場合，変化前
では同じ合流点内のすべての信号機は赤である．

問題5：信号機（つづき）
? 事例の確認
– 1つの合流点，高々3台の信号機の場合で，事例を確
認する．
– 同じスコープで，有効な信号変化の事例を確認する．
– 同じスコープで，合流点に存在する信号機が2台以上
かつ，いずれかの信号機が赤から別の色に信号が変
化する場合だけを取り出して，確認する．
? 反例の確認
– 同じスコープで，同じ合流点に設置された信号機の
中で，赤でない信号機の数は高々1つであるかどうか，
反例を確認する．
– 前項の制約3または制約4を外して反例を確認する．

色，信号機，合流点
// 色の定義
enum Color {Red, Yellow, Green}
// 正しい色の順番を示す関係，を返す関数
fun colorSequence: Color -> Color {
Color <: iden + Red->Green + Green->Yellow + Yellow->Red
}
// 信号機の集合
sig Light {}
// 信号機の状態．
sig LightState {color: Light -> one Color}
// 合流点．
sig Junction {lights: set Light}

制約の記述
// 赤の信号機の集合を返す関数
fun redLights [s: LightState]: set Light { s.color.Red }
// 合流点に存在する信号機のうち，赤でないものは高々1つ．
pred mostlyRed [s: LightState, j: Junction] {
lone j.lights - redLights[s]
}
// 信号機の変化
pred trans [s, s': LightState, j: Junction] {
// 合流点に存在するライトのうち，色が変化するものは高々一つ
lone x: j.lights | s.color[x] != s'.color[x]
all x: j.lights | let step = s.color[x] -> s'.color[x] {
// 合流点に存在する信号はすべて，決められた色の変化をする．
step in colorSequence
// ある信号機が赤から赤以外へ変化する場合，
// 変化前では同じ合流点内のすべての信号機は赤である
step in Red->(Color-Red) => j.lights in redLights[s]
}
}

事例の確認
// 可能性のある組合せを表示する．
run {} for 3 but 1 Junction
// 有効な信号変化の事例を表示してみる
run trans for 3 but 1 Junction
// 信号変化のうち，特定の部分だけを取り出してみる．
pred show[s, s': LightState, j: Junction] {
// 信号機が変化する条件を満たす
trans[s, s', j]
// 合流点に存在する信号機の数が2つ以上
all j: Junction | #(j.lights) >= 2
// 合流点に存在する信号機のうち，
// 少なくとも一つが赤から別の色に変化する場合
some x: j.lights| s.color[x] -> s'.color[x] in Red -> (Color-Red)
}
run show for 3 but 1 Junction

事例の表示
? run show for 3 but 1 Junction の表示例
– 操作trans により状態がLightState2 から
LightState1 へ変化したことを示している

事例の表示(2)
? 複雑な表示は，特定のシグネチャの表示を省く
ことで，見やすくなる．
– 元の順序対から指定要素を省いてできる，新たな順
序対を図示したものになる
変化後
ここを押す

assert,checkによる反例の確認
// 安全の要件
// すべての合流点とその信号機に対して，
// 赤でない状態の信号機は高々一つであり，
// かつ，それが状態変化しても，赤でない信号機は高々一つである
assert Safe {
all s, s': LightState, j: Junction |
mostlyRed [s, j] and trans [s, s', j] => mostlyRed [s', j]
}
// 合流点が一つ，及び，色，信号機，信号機の状態が
// 高々3つの場合において安全か
check Safe for 3 but 1 Junction

反例の表示
? 制約3を外すと，2つの信号が同時に赤から青へ
変化するケースが存在することが判明した．

行ったこと
? Alloy の概要について紹介した．
? いくつかの例をもとに，Alloy ツールを実際に
使用した．
– Alloy 言語を使用してモデルの記述を行った．
– Alloy 解析器を使用してモデルの事例及び反例を導出
し，結果を図で確認した．

その他，触れられなかったこと
? 整数値の扱い
– Alloy ではInt というシグネチャが用意済み．
– Int の要素を整数値に変換する演算子としてint，整
数値をIntの要素に変換する演算子としてIntが利用可
– スコープ指定ではInt でInt アトムの要素数を，int
で(符号付き)整数値のビット幅を指定する．
– 整数を扱う演算はutil/integer をopen して使う．
? seq X (X は任意)
– Int -> X の関係を生成する．列の定義に使う．
? private
– モジュール外から参照できないsig,fun,predをつくる
? 以下に，簡単に情報がまとめられている
http://alloy.mit.edu/alloy/documentation/quickguide/index.html

所感
? 関係を基にしたモデルの記述は慣れが必要かも
? 関係をもとに整理されており，構文要素が少な
いため覚えるのはあまり苦労しないで済んだ．
– モデルの文法エラーで悩むことがあまりなかった
? ツールにより事例及び反例のチェックを容易に
おこなうことができた
? 新しい版に対する情報が散在している印象があ
り，リファレンスが欲しいと思うことがあった．
当時の話です．今はどうですかね？
– 新しい版に対する完全なリファレンスは存在しない．
? 文献[1]は古いバージョン(4より前)に基づいている．
– 文法変更が今後もしばしば生じる可能性がある．

狠狠撸

サンプルで学ぶ础濒濒辞测

More Related Content

サンプルで学ぶ础濒濒辞测