1. df tests

Oct 15, 20121 like793 views

This document discusses the Dickey-Fuller test for unit roots, which tests whether a time series is stationary or nonstationary. It presents the three regression equations used in the Dickey-Fuller test and the corresponding critical values. It then provides steps for performing the Dickey-Fuller test in EViews, including specifying the test type, level/difference of the series, regression model, lag length, and interpreting the test results by comparing the test statistic to the critical values.

Data Analysis & Forecasting Faculty of Development Economics

NONSTATIONARY & UNIT ROOTS
DICKEY-FULLER TESTS

1. DF Test Equations
The simple Dickey-Fuller test is based on the following AR(1) model:
Yt = ρYt-1 + ut (*)
H0: ρ = 1 (Yt has a unit root ~ Yt is nonstationary)
H1: ρ < 1 (Yt does not have a unit root ~ Yt is stationary)
If we subtract Yt-1 from both sides of (*):
Yt – Yt-1 = ρYt-1 – Yt-1 + ut
∆Yt = (ρ - 1)Yt-1 + ut
∆Yt = δYt-1 + ut (1)
H0: ρ = 1 (Yt has a unit root ~ Yt is nonstationary)
H1: ρ < 1 (Yt does not have a unit root ~ Yt is stationary)
Dickey and Fuller (1979) also proposed two alternative regression equations that
can be used for testing for the presence of a unit root.
The first contains a constant in the random walk process as in the following
equation:
∆Yt = α + δYt-1 + ut (2)
The second case is also allow, a non-stochastic time trend in the model, so as
to have:
∆Yt = α + γT + δYt-1 + ut (3)
This test does not have a conventional ‘t’ distribution and so we must use special
critical values which were originally calculated by Dickey and Fuller.
MacKinnon (1991,1996) tabulated appropriate critical values for each of the
three above models and these are presented in Table 1.
Table 1: Critical values for DF test
Model 1% 5% 10%
∆Yt = δYt-1 + ut -2.56 -1.94 -1.62
∆Yt = α + δYt-1 + ut -3.43 -2.86 -2.57
∆Yt = α + γT + δYt-1 + ut -3.96 -3.41 -3.13
Standard critical values -2.33 -1.65 -1.28
Source: Asteriou (2007)

Phung Thanh Binh (2010) 1

Data Analysis & Forecasting Faculty of Development Economics

If the DF statistical value is smaller in absolute terms than the critical value then
we reject the null hypothesis of a unit root and conclude that Yt is a stationary
process.
2. Performing DF Test in Eviews
Step 1 Open the file DF.wf1 by clicking File/Open/Workfile and then
choosing the file name from the appropriate path

Step 2 Let’s assume that we want to examine whether the series named GDP
contains a unit root. Double click on the series named ‘GDP’ to open
the series window and choose View/Unit Root Test …. In the unit-
root test dialog box that appears, choose the type test (i.e., the
Augmented Dickey-Fuller test) by clicking on it.

Step 3 We then specify whether we want to test for a unit root in the level,
first difference, or second difference of the series. We can use this
option to determine the number of unit roots in the series.

Step 4 We also have to specify which model of the three DF models we wish
to use. For the model given by equation (1) click on ‘none’ in the
dialog box; for the model given by equation (2) click on ‘intercept’;
and for the model given by equation (3) click on ‘intercept and
trend’.

Step 5 Type ‘0’ on the ‘user specified’ below the “lag length’ dialog box.

Step 6 Having specified these options, click <OK> to carry out the test.

Step 7 We reject the null hypothesis of a unit root against the one-sided
alternative if the DF statistic is less than (lies to the left of) the critical
value, and we conclude that the series is stationary.

Source: Asteriou (2007)

Phung Thanh Binh (2010) 2

The document summarizes the Toda-Yamamoto augmented Granger causality test. [1] The test allows checking for causality between integrated variables of different orders without needing to determine cointegration. It involves estimating a VAR model with maximal order of integration lags added. [2] The test procedure involves determining the order of integration (d), selecting the optimal lag length (k), setting the null and alternative hypotheses of no causality and causality, and calculating an F-statistic to test for causality. [3] If the F-statistic exceeds the critical value, the null of no causality is rejected, indicating causality between the variables.

6. bounds test for cointegration within ardl or vecm Quang Hoang

��

This document discusses using the bounds test approach within an autoregressive distributed lag (ARDL) model to test for cointegration and causality between time series variables. The ARDL model estimates error correction models involving the change in one variable (ΔYt or ΔXt) regressed on lags of itself and the other variable. The bounds test involves calculating an F-statistic and comparing it to critical value bounds - if the F-statistic exceeds the upper critical value bounds, then there is cointegration, and if it falls below the lower bounds, then there is no cointegration. The document provides the null and alternative hypotheses for the bounds test when each variable is the dependent variable in the error correction model. It also outlines the

4. standard granger causalityQuang Hoang

��

The document describes the standard Granger causality test procedure for determining whether changes in one time series (Xt) can help forecast changes in another (Yt). [1] The test involves estimating a VAR model with the two time series and their lags, then comparing the restricted and unrestricted models to calculate an F-statistic. [2] If the F-statistic exceeds the critical value, the null hypothesis that Xt does not help forecast Yt (or vice versa) is rejected, indicating Granger causality between the two time series. [3] The test results help explain the relationship between the changes in the two time series by determining the direction of causality (if any

5. cem granger causality ecm Quang Hoang

��

The document describes the error correction model (ECM) version of Granger causality testing for determining the causal relationship between two non-stationary time series variables. It involves first testing for cointegration between the variables using the Johansen test or Engle-Granger approach. If cointegrated, the ECM version estimates an error correction model and performs Granger causality tests to examine short-run, long-run, and strong causality. The procedure and hypotheses for each test are provided along with the method for calculating the relevant F-statistics.

2. adf testsQuang Hoang

��

The document discusses augmented Dickey-Fuller (ADF) tests for detecting unit roots in time series data. It presents the three possible forms of the ADF test regression and describes how to determine the appropriate model. A procedure is outlined for selecting between models and testing whether time series contain deterministic trends, constants, or unit roots. The document also provides instructions for performing ADF tests in Eviews software, including specifying the test regression, lag length, and interpreting the test results.

Co-integration Suniya Sheikh

��

The document discusses the concept of cointegration and its various approaches, particularly focusing on the Engle-Granger and Johansen-Juselius methods. It outlines the conditions necessary for cointegration, interpretations of the Error Correction Model (ECM), and provides steps for conducting estimations using these methodologies. Additionally, it includes examples, definitions, and references for further reading on the subject.

Propensity albertJae-kwang Kim

��

This document proposes an approximate Bayesian inference method for estimating propensity scores under nonresponse. It involves treating the estimating equations as random variables and assigning a prior distribution to the transformed parameters. Samples are drawn from the posterior distribution of the parameters given the observed data to make inferences. The method is shown to be asymptotically consistent and confidence regions can be constructed from the posterior samples. Extensions are discussed to incorporate auxiliary variables and perform Bayesian model selection by assigning a spike-and-slab prior over the model parameters.

Chapter2: Likelihood-based approach Jae-kwang Kim

��

This document summarizes key concepts from Chapter 2 of a book on statistical methods for handling incomplete data. It introduces the likelihood-based approach and defines key terms like the likelihood function, maximum likelihood estimator, Fisher information, and missing at random. The chapter also provides examples of observed likelihood functions for censored regression and survival analysis models with missing data.

F023064072inventionjournals

��

This document discusses the duality between initial and terminal function problems for single-delay autonomous linear control systems. It presents theorems from previous work by Ukwu and Garba that provide solution matrices and indices of control systems. The paper establishes that the initial and terminal function problems are topological duals of each other by outlining transformations that can be used to obtain the solution matrix for one problem from the solution matrix of the other problem. This is achieved through key operations including changing variables, integrals, and exponential functions in the solution matrix formulas. The transformations effectively show that results from one problem can be realized from the other, demonstrating the duality between the initial and terminal function problems.

Lesson 15: Exponential Growth and DecayMatthew Leingang

��

This document contains lecture notes on exponential growth and decay from a Calculus I class at New York University. It begins with announcements about an upcoming review session, office hours, and midterm exam. It then outlines the topics to be covered, including the differential equation y=ky, modeling population growth, radioactive decay including carbon-14 dating, Newton's law of cooling, and continuously compounded interest. Examples are provided of solving various differential equations representing exponential growth or decay. The document explains that many real-world situations exhibit exponential behavior due to proportional growth rates.

Lesson 13: Related Rates ProblemsMatthew Leingang

��

This document contains notes from a Calculus I class at New York University. It discusses related rates problems, which involve taking derivatives of equations relating changing quantities to determine rates of change. The document provides examples of related rates problems involving an oil slick, two people walking towards and away from each other, and electrical resistors. It also outlines strategies for solving related rates problems, such as drawing diagrams, introducing notation, relating quantities with equations, and using the chain rule to solve for unknown rates.

On the stability and accuracy of finite difference method for options pricingAlexander Decker

��

1) The document discusses finite difference methods for pricing options, specifically the implicit and Crank-Nicolson methods. 2) It analyzes the stability and accuracy of each method. The Crank-Nicolson method is found to be more accurate and converges faster than the implicit method. 3) Numerical examples are provided to demonstrate the convergence properties of each method compared to the true Black-Scholes value. The results show that the Crank-Nicolson method converges to the solution faster than the implicit method as the time and price steps approach zero.

The Fundamental theorem of calculus AhsanIrshad8

��

The document discusses the Fundamental Theorem of Calculus, which has two parts. Part 1 establishes the relationship between differentiation and integration, showing that the derivative of an antiderivative is the integrand. Part 2 allows evaluation of a definite integral by evaluating the antiderivative at the bounds. Examples are given of using both parts to evaluate definite integrals. The theorem unified differentiation and integration and was fundamental to the development of calculus.

11.the comparative study of finite difference method and monte carlo method f...Alexander Decker

��

This document compares the finite difference method and Monte Carlo method for pricing European options. It provides an overview of these two primary numerical methods used in financial modeling. The Monte Carlo method simulates asset price paths and averages discounted payoffs to estimate option value. It is well-suited for path-dependent options but converges slower than finite difference. The finite difference method solves the Black-Scholes PDE by approximating it on a grid. Specifically, it discusses the Crank-Nicolson scheme, which is unconditionally stable and converges faster than Monte Carlo for standard options.

А.Н. Ширяев "Обзор современных задач об оптимальной обстановке"Yandex

��

This document outlines a series of lectures on stochastic optimization, focusing on topics such as quickest detection problems, optimal stopping theory, and stochastic differential equations. It includes discussions on both discrete and continuous time scenarios, highlighting various models and methodologies for solving optimization problems in financial statistics. Key concepts and historical contributions to the field are referenced, including works by W. Shewhart and E. Page.

Predictive mean-matching2Jae-kwang Kim

��

This document discusses predictive mean matching (PMM) imputation in survey sampling. It begins with an outline and overview of the basic setup, assumptions, and PMM imputation method. It then presents three main theorems: 1) the asymptotic normality of the PMM estimator when the regression parameter β* is known, 2) the asymptotic normality when β* is estimated, and 3) the asymptotic properties of nearest neighbor imputation. The document also discusses variance estimation for the PMM estimator using replication methods like the bootstrap or jackknife. In summary, it provides a theoretical analysis of the asymptotic properties of PMM imputation and approaches for estimating the variance.

MNARJae-kwang Kim

��

This document summarizes several statistical methods for handling non-ignorable nonresponse in data, including maximum likelihood estimation, partial likelihood approaches, generalized method of moments, and exponential tilting methods. It discusses full likelihood-based maximum likelihood estimation using the observed data likelihood and EM algorithm. Partial likelihood approaches like conditional likelihood and pseudo likelihood are presented as alternatives that use a subset of the observed data.

Principal Component Analysis for Tensor Analysis and EEG classificationTatsuya Yokota

��

The document details tensor analysis techniques for EEG data in the context of brain-computer interfaces (BCIs), emphasizing the importance of non-invasive methods like EEG due to their low cost and risk. It outlines steps in EEG analysis, introduces tensor calculations and decompositions, and presents experimental results comparing different classification methods. The findings are based on data obtained from a BCI competition involving motor imagery classification.

Quantum Minimax Theorem in Statistical Decision Theory (RIMS2014)tanafuyu

��

This document presents a presentation on the quantum minimax theorem in statistical decision theory, focusing on Bayesian statistics and its differences from traditional frequentist statistics. The discussion outlines the roles of prior distributions, statistical models, and measurement techniques within quantum mechanics, and proposes a framework for quantum Bayesian hypothesis testing. It concludes with a detailed overview of the quantum minimax theorem and its implications for optimal decision-making under uncertainty.

Lecture on solving1NBER

��

The document discusses methods for solving dynamic stochastic general equilibrium (DSGE) models. It outlines perturbation and projection methods for approximating the solution to DSGE models. Perturbation methods use Taylor series approximations around a steady state to derive linear approximations of the model. Projection methods find parametric functions that best satisfy the model equations. The document also provides an example of applying the implicit function theorem to derive a Taylor series approximation of a policy rule for a neoclassical growth model.

Lesson 21: Antiderivatives (notes)Matthew Leingang

��

The document provides comprehensive notes on antiderivatives in Calculus I, covering definitions, methods of finding antiderivatives for various functions (polynomials, exponential, trigonometric), and applications in motion problems. It outlines key theorems, including how antiderivatives relate to the original function's derivatives and discusses graphical interpretations. Additionally, it includes examples and problems to illustrate the concepts covered.

Linked CP Tensor Decomposition (presented by ICONIP2012)Tatsuya Yokota

��

This document proposes a new method called Linked Tensor Decomposition (LTD) to analyze common and individual factors from a group of tensor data. LTD combines the advantages of Individual Tensor Decomposition (ITD), which analyzes individual characteristics, and Simultaneous Tensor Decomposition (STD), which analyzes common factors in a group. LTD represents each tensor as the sum of a common factor and individual factors. An algorithm using Hierarchical Alternating Least Squares is developed to solve the LTD model. Experiments on toy problems and face reconstruction demonstrate LTD can extract both common and individual factors more effectively than ITD or STD alone. Future work will explore Tucker-based LTD and statistical independence in the LTD model

The Odd Generalized Exponential Log Logistic Distributioninventionjournals

��

The document introduces a new lifetime model called the odd generalized exponential log-logistic distribution (OGELLD), which combines features of generalized exponential and log-logistic distributions. It discusses the mathematical properties and parameters of OGELLD, including estimation methods and applications to real lifetime data. The paper further elaborates on the distribution functions, statistical properties, and potential use in reliability studies.

Nber slides11 lecture2NBER

��

This document discusses various machine learning techniques including: 1. Tree pruning involves first growing a large tree and then pruning branches that do not improve the objective function. This prevents early stopping. 2. Boosting uses multiple weak learners sequentially to get an additive model that approximates the regression function. It combines many simple models to create a powerful ensemble model. 3. Unsupervised learning techniques like principal component analysis and clustering are used to find patterns in data without an outcome variable. These include reducing dimensions and partitioning data into subgroups.

Chapter 2the_satellite

��

1) The document discusses limits, continuity, and tangent lines. It provides definitions of limits and continuity, and examples of evaluating one-sided limits. 2) Methods for computing limits of polynomials, rational functions, and piecewise functions are presented along with theorems about continuity of functions. 3) The concept of asymptotes is introduced as limits involving infinity. Examples of evaluating various types of limits are worked out.

Presentation03 ssnashaat algrara

��

This document presents an overview of the differential transform method (DTM) for solving differential equations. DTM uses Taylor series to obtain approximate or exact solutions. The document defines 1D, 2D, and 3D DTM and lists common operations. Examples are provided of applying DTM to solve systems of linear/non-linear differential equations. The document concludes with references for further applications of DTM in engineering and mathematics.

Free Ebooks Download ! EdholeEdhole.com

��

The document discusses various topics related to differential equations including: 1. Linear differential equations of nth order with constant coefficients and the characteristic equation. The general solution depends on whether the roots of the characteristic equation are real/complex, distinct/multiple. 2. Finding the complementary function and particular integral to get the general solution for a second order differential equation with constant coefficients. 3. Solving simultaneous linear differential equations using the D-operator method and Laplace transform method. 4. Changing dependent and independent variables to solve second order differential equations numerically using an approximation technique similar to the trapezoid rule.

201977 1-1-2-pbAssociateProfessorKM

��

This document presents algorithms for solving overdetermined systems of linear equations using the L1 norm. It begins with algorithms for weighted median regression (1 parameter model) and simple linear regression (2 parameter model). It then presents a general algorithm for multiple linear regression with m parameters. Computer programs in Fortran are provided for each algorithm to compute the L1 norm solution efficiently. Key steps include sorting ratios, accumulating weights, and using a weighted median function to find the optimal solution at each iteration.

Unit Root Test Suniya Sheikh

��

The document provides an overview of unit root tests in time series analysis, explaining the concept of a unit root, how to check for it, and detailing three types of tests: Dickey-Fuller, Augmented Dickey-Fuller, and Phillips-Perron. It outlines the procedure to test for non-stationarity in autoregressive models and offers a step-by-step guide on conducting unit root tests using E-Views software. The referenced materials suggest further reading in applied and basic econometrics.

isiahfdv

��

This document reviews testing for causality between variables. It begins by defining Granger causality, which tests whether including one time series helps forecast another. For bivariate systems, causality can be tested by examining coefficients in a vector autoregression (VAR) model. For multivariate systems, causality is more complex and graphical models may help. The document outlines procedures for testing causality between stationary and nonstationary time series using impulse responses, vector autoregressive moving average (VARMA) models, and other techniques. It provides examples and discusses challenges like potential omitted common factors.

More Related Content

What's hot (20)

F023064072inventionjournals

��

Lesson 15: Exponential Growth and DecayMatthew Leingang

��

Lesson 13: Related Rates ProblemsMatthew Leingang

��

On the stability and accuracy of finite difference method for options pricingAlexander Decker

��

The Fundamental theorem of calculus AhsanIrshad8

��

11.the comparative study of finite difference method and monte carlo method f...Alexander Decker

��

А.Н. Ширяев "Обзор современных задач об оптимальной обстановке"Yandex

��

Predictive mean-matching2Jae-kwang Kim

��

MNARJae-kwang Kim

��

Principal Component Analysis for Tensor Analysis and EEG classificationTatsuya Yokota

��

Quantum Minimax Theorem in Statistical Decision Theory (RIMS2014)tanafuyu

��

Lecture on solving1NBER

��

Lesson 21: Antiderivatives (notes)Matthew Leingang

��

Linked CP Tensor Decomposition (presented by ICONIP2012)Tatsuya Yokota

��

The Odd Generalized Exponential Log Logistic Distributioninventionjournals

��

Nber slides11 lecture2NBER

��

Chapter 2the_satellite

��

Presentation03 ssnashaat algrara

��

Free Ebooks Download ! EdholeEdhole.com

��

201977 1-1-2-pbAssociateProfessorKM

��

F023064072inventionjournals

��

Lesson 15: Exponential Growth and DecayMatthew Leingang

��

Lesson 13: Related Rates ProblemsMatthew Leingang

��

On the stability and accuracy of finite difference method for options pricingAlexander Decker

��

The Fundamental theorem of calculus AhsanIrshad8

��

11.the comparative study of finite difference method and monte carlo method f...Alexander Decker

��

А.Н. Ширяев "Обзор современных задач об оптимальной обстановке"Yandex

��

Predictive mean-matching2Jae-kwang Kim

��

MNARJae-kwang Kim

��

Principal Component Analysis for Tensor Analysis and EEG classificationTatsuya Yokota

��

Quantum Minimax Theorem in Statistical Decision Theory (RIMS2014)tanafuyu

��

Lecture on solving1NBER

��

Lesson 21: Antiderivatives (notes)Matthew Leingang

��

Linked CP Tensor Decomposition (presented by ICONIP2012)Tatsuya Yokota

��

The Odd Generalized Exponential Log Logistic Distributioninventionjournals

��

Nber slides11 lecture2NBER

��

Chapter 2the_satellite

��

Presentation03 ssnashaat algrara

��

Free Ebooks Download ! EdholeEdhole.com

��

201977 1-1-2-pbAssociateProfessorKM

��

Similar to 1. df tests (20)

Unit Root Test Suniya Sheikh

��

isiahfdv

��

Cointegration analysis: Modelling the complex interdependencies between finan...Edward Thomas Jones

��

1) The document discusses cointegration analysis, which models the complex interdependencies between financial assets. It examines the non-stationary nature of financial time series data and explores vector autoregressive (VAR) models and cointegration techniques to analyze relationships between non-stationary variables. 2) VAR models provide a framework for modeling dynamic relationships between stationary time series variables. The document outlines univariate and multivariate VAR models and discusses estimations and lag order selection for VAR models. 3) Cointegration techniques allow modeling of relationships between non-stationary time series variables. The document reviews tests for identifying stationary and non-stationary time series, including the Augmented Dickey-Fuller and Phillips-Perron tests

Issues in time series econometricsBabu Tyagu

��

This document discusses concepts and techniques for time series analysis. It defines a time series as any series of data that varies over time, and provides examples like GDP and stock prices. It outlines precautions for using time series data in econometric models, such as checking for stationarity and guarding against spurious regressions. Stationary and non-stationary time series are defined, and unit root tests like the Dickey-Fuller test are introduced. The concepts of cointegration and error correction models are also covered, along with the Granger causality test.

Unit Root TestSuniya Sheikh

��

The document outlines the concept of unit root tests, including definitions and methodologies for testing non-stationarity in time series data using tests such as the Dickey-Fuller, Augmented Dickey-Fuller, and Phillips-Perron tests. It provides a step-by-step approach to conducting these tests and highlights the differences among these tests regarding autocorrelation and heteroskedasticity. Additionally, it emphasizes the importance of graphical analysis as a preliminary step in time series analysis.

Ch8 slidesfentaw leykun

��

This document discusses testing for non-stationarity and unit roots in time series data. It introduces the Augmented Dickey-Fuller (ADF) test and Phillips-Perron test for determining if a time series is integrated of order zero (I(0)), one (I(1)), or two (I(2)). The ADF test regressions the change in a variable on its lag and lags of the change to test for a unit root. If the null of a unit root is not rejected, further tests are needed to determine higher orders of integration. While ADF and Phillips-Perron tests are commonly used, their power is low if the process is near but not at the non-station

Ch8_slides.pptQUNHHUNHTRNTRC

��

ders 3.3 Unit root testing section 3 .pptxErgin Akalpler

��

The document discusses various unit root tests used to determine if a time series is stationary or non-stationary. It describes the Dickey-Fuller test and Augmented Dickey-Fuller test, which test for a unit root in a time series. The Augmented Dickey-Fuller test extends the Dickey-Fuller test by including lagged difference terms to account for autocorrelation. The tests are used to distinguish between trend-stationary and difference-stationary processes, which have different implications for forecasting and detecting spurious relationships between variables.

11��T(EA) FOR TWO��TESTS BETWEEN THE MEANS OF DIFFERENT GROUPS11 .docxnovabroom

��

This document discusses the use of the t-test for independent means in comparing the prevalence and intensity of eating disorders between Indian and Australian university students. It highlights significant differences in test scores, with Indian students scoring higher, and emphasizes the importance of understanding the t-test calculation, interpretation of the p-value, and effect size in the analysis. The document also outlines the methodological steps involved in conducting a t-test, including formulating hypotheses, calculating the t value, and making decisions based on critical values.

Multivariate decision treePrafulla Shukla

��

The document discusses C4.5 algorithm for building univariate decision trees and methods for building multivariate decision trees. C4.5 uses entropy, gain, and pruning to build trees that classify instances based on one attribute per node. Multivariate trees can classify using linear combinations of attributes at nodes to better handle correlated attributes. Methods like absolute error correction and thermal perceptron are presented for training linear machines to construct multivariate trees. Examples of trees generated by both approaches are shown.

modelling lon run relationship in financetilfani

��

The document discusses the importance of testing for stationarity in economic time series data to prevent issues such as spurious regression and invalid hypothesis testing. It explains different types of non-stationarity, methods for inducing stationarity through differencing, and key statistical tests like the Dickey-Fuller and Phillips-Perron tests for unit roots. It also emphasizes the significance of distinguishing between different levels of integration (i(0), i(1), i(2)) and the potential need for multiple differencing to achieve stationarity.

Estimation of Dynamic Causal Effects -Introduction to EconomicsNgocducPham1

��

better together? statistical learning in models made of modulesChristian Robert

��

The document discusses statistical models composed of modular components called modules. Each module may be developed independently and represent different data modalities or domains of knowledge. Joint Bayesian updating treats all modules simultaneously but misspecification of one module can impact the others. Alternative approaches are proposed to allow uncertainty propagation between modules while preventing feedback that could lead to misspecification. Candidate distributions for the modules are discussed, along with strategies for choosing among them based on predictive performance.

Asset Prices in Segmented and Integrated Marketsguasoni

��

This document summarizes a model of asset pricing in segmented and integrated markets. It begins with motivation from the financialization of commodities and market integration. It then presents a model with two regions/trees producing dividends. Equilibria are characterized for when the regions are segmented and integrated. Key results include asset prices being more cyclical and negatively correlated in segmentation, but highly positively correlated in integration. Integration always increases welfare even if it sometimes lowers asset prices and total wealth. Both regions would choose integration to access a smoother consumption stream.

SPM 12 practical course by Volodymyr B. Bogdanov (Kyiv 2015, Day 2) Volodymyr Bogdanov

��

This document discusses statistical analysis of fMRI data from a 2-factor study on face recognition. It covers: - Designing categorical and parametric models to analyze effects of factors "fame" and "repetition" of faces. - Specifying contrasts to compare conditions and estimate main effects and interactions. - Understanding design matrices, basis functions, and statistical tables from the analysis. - Performing first-level analysis on individual data and second-level analysis to make inferences about the study population.

Cointegration among biotech stocksPeter Zobel

��

This document is a thesis that examines potential cointegration among biotech stocks. It begins with an introduction that provides background on cointegration and discusses how little is known about cointegration of individual stocks. The document then reviews relevant theoretical frameworks for unit root testing and cointegration testing. It also discusses characteristics of biotech stocks and criteria for stock valuation. The empirical analysis will apply unit root and cointegration tests to selected biotech stock data. The results may provide insights into whether these stocks share a common stochastic trend.

Brown bag 2012_fallXiaolei Zhou

��

- The document describes a study that uses eye tracking to analyze how people search for information when making decisions. It presents information in a table where cells are initially obscured and revealed when a person's eyes fixate on that cell. - Existing analysis of search dynamics focuses on summary statistics rather than detailed measurements of the search process. The presenter aims to develop new metrics using techniques from other fields to better analyze the high-resolution eye tracking data. - String edit distance and hierarchical log-linear modeling are proposed as potential approaches to differentiate search strategies, analyze effects of experimental conditions, and test whether models describe actual search behavior observed in the eye tracking data.

Estimation of Static Discrete Choice Models Using Market Level DataNBER

��

This document discusses methods for estimating static discrete choice models using market-level data rather than individual consumer data. It covers several key topics: 1) The types of market-level and consumer-level data that can be used. Market-level data is easier to obtain but poses challenges for identification and estimation. 2) A common linear random coefficients logit model framework. It includes observed and unobserved product characteristics as well as observed and unobserved consumer heterogeneity. 3) The key challenges of estimating heterogeneity parameters without consumer-level data. It also discusses how to deal with potential endogeneity of unobserved product characteristics. 4) The two-step estimation approach when consumer-level data is available, and

Exponential lindley additive failure rate modeleSAT Journals

��

This document presents an exponential-Lindley additive failure rate model (ELAFRM) by combining the hazard functions of an exponential distribution and a Lindley distribution. The key properties of the ELAFRM are derived, including the probability density function, cumulative distribution function, hazard function, moments, and graphical representations. Estimation of the model parameters is also discussed. The document proposes this new ELAFRM distribution and analyzes its mathematical properties.

Lecture06_Regression and optimization.pdfShafinZaman2

��

The lecture discusses linear regression, focusing on predicting continuous outputs such as movie ratings, house prices, and social media followers. Key components of regression include features (inputs), training examples, models (to represent relationships), and optimization techniques to minimize loss functions. The presentation also addresses challenges like noise in data, model complexity, generalization, and the choice of appropriate models and loss functions.

Unit Root Test Suniya Sheikh

��

isiahfdv

��

Cointegration analysis: Modelling the complex interdependencies between finan...Edward Thomas Jones

��

Issues in time series econometricsBabu Tyagu

��

Unit Root TestSuniya Sheikh

��

Ch8 slidesfentaw leykun

��

Ch8_slides.pptQUNHHUNHTRNTRC

��

ders 3.3 Unit root testing section 3 .pptxErgin Akalpler

��

11��T(EA) FOR TWO��TESTS BETWEEN THE MEANS OF DIFFERENT GROUPS11 .docxnovabroom

��

Multivariate decision treePrafulla Shukla

��

modelling lon run relationship in financetilfani

��

Estimation of Dynamic Causal Effects -Introduction to EconomicsNgocducPham1

��

better together? statistical learning in models made of modulesChristian Robert

��

Asset Prices in Segmented and Integrated Marketsguasoni

��

SPM 12 practical course by Volodymyr B. Bogdanov (Kyiv 2015, Day 2) Volodymyr Bogdanov

��

Cointegration among biotech stocksPeter Zobel

��

Brown bag 2012_fallXiaolei Zhou

��

Estimation of Static Discrete Choice Models Using Market Level DataNBER

��

Exponential lindley additive failure rate modeleSAT Journals

��

Lecture06_Regression and optimization.pdfShafinZaman2

��

1. df tests

1. Data Analysis & Forecasting Faculty of Development Economics NONSTATIONARY & UNIT ROOTS DICKEY-FULLER TESTS 1. DF Test Equations The simple Dickey-Fuller test is based on the following AR(1) model: Yt = ρYt-1 + ut (*) H0: ρ = 1 (Yt has a unit root ~ Yt is nonstationary) H1: ρ < 1 (Yt does not have a unit root ~ Yt is stationary) If we subtract Yt-1 from both sides of (*): Yt – Yt-1 = ρYt-1 – Yt-1 + ut ∆Yt = (ρ - 1)Yt-1 + ut ∆Yt = δYt-1 + ut (1) H0: ρ = 1 (Yt has a unit root ~ Yt is nonstationary) H1: ρ < 1 (Yt does not have a unit root ~ Yt is stationary) Dickey and Fuller (1979) also proposed two alternative regression equations that can be used for testing for the presence of a unit root. The first contains a constant in the random walk process as in the following equation: ∆Yt = α + δYt-1 + ut (2) The second case is also allow, a non-stochastic time trend in the model, so as to have: ∆Yt = α + γT + δYt-1 + ut (3) This test does not have a conventional ‘t’ distribution and so we must use special critical values which were originally calculated by Dickey and Fuller. MacKinnon (1991,1996) tabulated appropriate critical values for each of the three above models and these are presented in Table 1. Table 1: Critical values for DF test Model 1% 5% 10% ∆Yt = δYt-1 + ut -2.56 -1.94 -1.62 ∆Yt = α + δYt-1 + ut -3.43 -2.86 -2.57 ∆Yt = α + γT + δYt-1 + ut -3.96 -3.41 -3.13 Standard critical values -2.33 -1.65 -1.28 Source: Asteriou (2007) Phung Thanh Binh (2010) 1

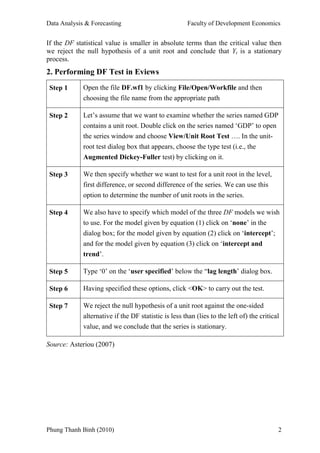
2. Data Analysis & Forecasting Faculty of Development Economics If the DF statistical value is smaller in absolute terms than the critical value then we reject the null hypothesis of a unit root and conclude that Yt is a stationary process. 2. Performing DF Test in Eviews Step 1 Open the file DF.wf1 by clicking File/Open/Workfile and then choosing the file name from the appropriate path Step 2 Let’s assume that we want to examine whether the series named GDP contains a unit root. Double click on the series named ‘GDP’ to open the series window and choose View/Unit Root Test …. In the unit- root test dialog box that appears, choose the type test (i.e., the Augmented Dickey-Fuller test) by clicking on it. Step 3 We then specify whether we want to test for a unit root in the level, first difference, or second difference of the series. We can use this option to determine the number of unit roots in the series. Step 4 We also have to specify which model of the three DF models we wish to use. For the model given by equation (1) click on ‘none’ in the dialog box; for the model given by equation (2) click on ‘intercept’; and for the model given by equation (3) click on ‘intercept and trend’. Step 5 Type ‘0’ on the ‘user specified’ below the “lag length’ dialog box. Step 6 Having specified these options, click <OK> to carry out the test. Step 7 We reject the null hypothesis of a unit root against the one-sided alternative if the DF statistic is less than (lies to the left of) the critical value, and we conclude that the series is stationary. Source: Asteriou (2007) Phung Thanh Binh (2010) 2

�ݺ�ߣ

1. df tests

Recommended

More Related Content

What's hot (20)

Similar to 1. df tests (20)

1. df tests