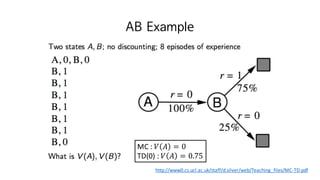
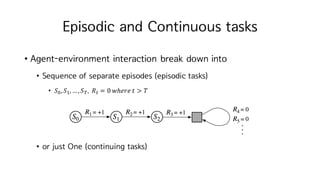
4. Episodic and Continuous tasks
? Agent-environment interaction break down into
? Sequence of separate episodes (episodic tasks)
? ?H, ?I,, ?K. ?M = 0 ????? ? > ?
? or just One (continuing tasks)
5. Value functions, V ?
? Estimate how good it is for the agent to be in a given state
? ?: ? ?
? how good is defined in terms of future rewards that can be expected
? ??? reward? ?? action????? ?? ???? (?)
? Vc
? = ?c
? ? ?M = ? = ?c ?h
?MihiI
KjM
hkH ?M = ?
? where Rl is the total return and ?l is a immediate reward
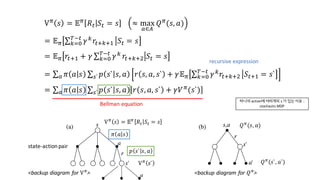
6. Vc
? = ?c
?M ?M = ? max
op
?c
(?, ?)
= ?c ?h
?MihiI
KjM
hkH ?M = ?
= ?c ?MiI + ? ?hKjM
hkH ?Mihit ?M = ?
= ? ? ? ? ?` ?, ? ? ?, ?, ?` + ??c ?h
?Mihit
KjM
hkH ?MiI = ?`w`o
= ? ? ? ? ?` ?, ? ? ?, ?, ?` + ??c
(?`)w`o
Bellman equation
state-action pair
? ?` ?, ?
? ? ?
Vc
? = ?c
?M ?M = ?
Vc
?`
recursive expression
?c
(?, ?)
?c
(?`, ?`)
<backup diagram for ?c
><backup diagram for Vc
>
??? action? ???? s ? ?? ?? :
stochastic MDP
7. Action-value functions, Q ?, ?
? The value of taking action ? in state ? under a policy ?
? ?: ? ?|?
? how good it is for the agent to be in taking action ? in state ? under a policy ?
? ?c
?, ? = ?c
?M ?M = ?, ?M = ? = ?c ?h
?MihiI
KjM
hkH ?M = ?, ?M = ?
? Optimal action-value function : ??
? = max
op(w)
??
(?, ?)
8. Optimal Value Functions
? Solving RL = finding an optimal policy
? ?? ? `?? ??? ?? ? ?? ? ?? ?? expected return? ?`?? ? ?
? ?c ? ?c`(?)
? ??
? = max
c
?c
?
? ??
?, ? = ???c ?c
(?, ?) : the expected return for taking action a in state s
? Express ??
in terms of ??
??
?, ? = ? ?h
?MihiI
KjM
hkH ?M = ?, ?M = ?
= ? ?MiI + ? ?hKjM
hkH ?Mihit ?M = ?, ?M = ?
= ? ?MiI + ? ??
(?MiI)|?M = ?, ?M = ?
= ?[?MiI + ? max
o`
? ?MiI, ?` |?M = ?, ?M = ?]
10. Bellman optimality equation
??
? = max
o
?[?MiI + ???
(?MiI)|?M = ?, ?M = ?]
= max
o
? ?` ?, ? [? ?, ?, ?` + ???
(?`)]w`
??
?, ? = ?[?MiI + ? max
o`
??
(?MiI, ?`)|?M = ?, ?M = ?]
= ? ?` ?, ? [? ?, ?, ?` + ? max
o`
??
?MiI, ?` ]w`
? For finite MDPs, Bellman optimality equation has a unique solution independent of the policy
? DP are obtained by turning Bellman equations into assignments
into update rules for improving approximations of value functions
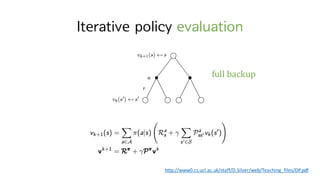
13. Policy Evaluation
? How to compute ?c
? for an arbitrary policy ?? ? ? value? ?? ?? ???
= policy evaluation
?c
? = ? ?M + ??c
?` ?M = ?
= ? ? ? ? ? ? ?` ?, ? [?(?, ?, ?`) + ??c
?` ]
w`o
?? ?? ?? future reward? expectation
14. Policy Evaluation
? ?? environment? ?? ??? ?? ??? (known MDP)
?c
? ?? |?|?? unknown variables (Vc
? , ? ?)? ???
|?|?? linear equations
? ??? arbitrary approximate value function ? ?H??? ??. ?H, ?I, ?t,
?hiI ? = ? ?M + ??h ?` ?M = ?
= ? ? ? ? ? ? ?` ?, ? [?(?, ?, ?`) + ??h ?` ]
w`o
<Iterative policy evaluation>
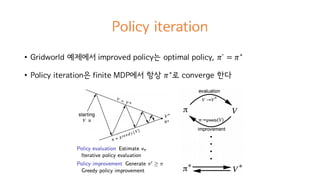
20. Policy improvement
? Policy evaluation ? ??? ? ?? policy? ?? ??
? Policy evaluation?? Arbitrary ?? ?? Vc
? ? ??
? ?? ? ?? ?? policy ? ? ??? ??? ??? Vc
? ?? ??
? ?? ? ?? policy ?`? ?????
? ??? ?`? ?` = ??????(?c) ? ?? ? ??
21. Policy improvement theorem
? ??? policy? ??? ?? ??? ????
?c ?, ? = ?c ?M ?M = ?, ?M = ?
= ?c ?h ?MihiI
KjM
hkH ?M = ?, ?M = ?
= ?c ?MiI + ?h ?MihiI
KjM
hkI ?M = ?, ?M = ? = ?c ?MiI + ??c(?`) ?M = ?, ?M = ?
? ?c ?, ?`(?) ? ?c(?)?? ??? ?`? ??? ??
?c ?, ?`(?) ?c ? for all ? ? ??,
?c` ? ?c ? for all ? ?. WHY?
?? value??? ?`? ??? value
? ?
?, ? = ? ? ?` ?, ? [? ?, ?, ?` + ?max
o`
? ?
?MiI, ?` ]
w`
24. ?c
? ? ??? ???, ? ?? ??
? ?? ???.
?? ? ?? ?? ?c
? ? ?` ?? ??? ? ??
26. Greedy policy
?` ? = argmax
o
?c(?, ?)
= argmax
o
?[?MiI + ??c
?MiI |?M = ?, ?M = ?]
= argmax
o
? ?` ?, ? [?(?, ?, ?`) + ??c
?` ]w`
? Greedy policy ? ?c
??? ? + 1?? ??? value? ??? action? ??
<Policy improvement theorem>
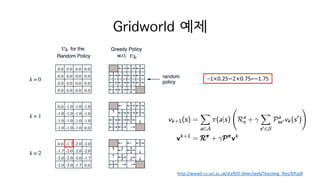
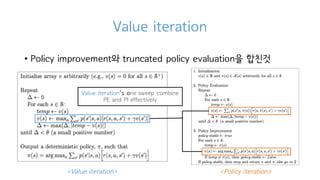
29. Value iteration
? Policy iteration? ??
? ?c
? ?????? Policy evaluation? converge ? ??? ?????
? ??? Gridworld ????? ??? ??
converge ? ? ?? ??? ??? ??
? ??? ?? ??? Value iteration
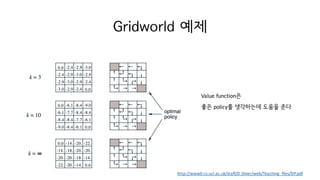
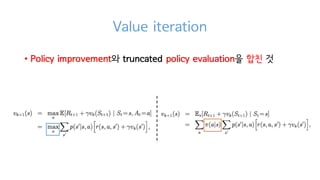
31. Value iteration
? Policy improvement? truncated policy evaluation? ???
<Policy iteration><Value iteration>
Value iteration's one sweep combine
PE and PI effectively
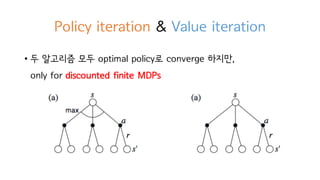
32. Policy iteration & Value iteration
? ? ???? ?? optimal policy? converge ???,
only for discounted finite MDPs
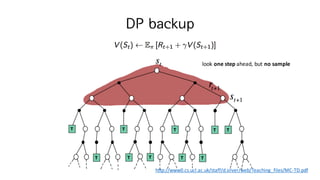
33. Asynchronous Dynamic Programming
? DP? ?? : MDP? ??? state? ?? ???? ??,
? ???? ???(converge ? ??? ????)? iteration ??
? State? ???? ???, ??? sweep? ?? expensive
? Asynchronous DP algorithm
? back up values of state in any order
? in-place dynamic programming
? prioritized sweeping
? real-time dynamic programming
34. In-Place Dynamic Programming
? Synchronous value iteration : ??? value function? ??
? ? max
op
? ?, ?, ?` + ? ? ? ?` ?, ? ?C?(?`)
w`?
?C? ?
? Asynchronous (In-place) value iteration : ?? ??? value function? ??
? ? max
op
? ?, ?, ?` + ? ? ? ?` ?, ? ?(?`)
w`?
35. Real-Time Dynamic Programming
? ??? agent? ???? state? ????
? Agent? experience? state ???? ???? ??
? ? time-step? Sl, ?M, ?MiI??
? ?M max
op
? ?M, ?, ?` + ? ? ? ?` ?M, ? ?(?`)
w`?
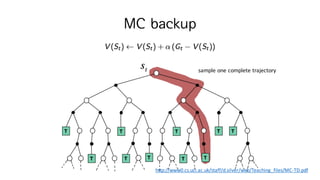
42. Monte-Carlo Reinforcement Learning
? Return : total discounted reward
GM = ?MiI + ??Mit + ?+ ?KiMjI
?K
? Value function : expected return reward
?c ? = ? ?M|?M = ?
? MC policy evaluation? expected return ?c ? ?
empirical mean return GM? ?????? ?? ?? ????
43. ? ?? ?? ??? ????
MC? ?? ?c
(?)? ???? ????
44. First-Visit MC Policy Evaluation
Episode ?? ?? with ?
?, ??? episode??s? ?? ?? ???? ????
? episode?? ??? N(s)? ??? ? ??
V(s), N(s), S(s)? ???? ????
45. Every-Visit MC Policy Evaluation
Episode ?? ?? with ?
? episode?? ??? N(s)? ??? ? ??
V(s), N(s), S(s)? ???? ????
46. Back to basic : Incremental Mean
?hiI =
I
h
??
h
?kI
=
I
h
?h + ??
hjI
?kI =
I
h
?h + (? ? 1 ?h + ?h ? ?h)
=
I
h
?h + ??h ? ?h = ?h +
I
h
?h ? ?h
? Only need memory for k and ?h
? General form:
??????????? ??????????? + ???????? ?????? ? ???????????
????? = ???????? ??????????
47. Incremental Monte-Carlo Updates
? ?I, ?I, ?I, , ?K? episode? ?? ?(?)? ???? ?? ??
? ? ?M? ?M? ???
? ?M ? ?M + 1
? ?M ? ?M +
1
? ?M
(?M ? ? ?M )
? non-stationary ???? fixed constant ?? ??? old episodes? ?? ?
??
? ?M ? ?M + ?(?M ? ? ?M )
?????
??? ??? ?? ??? ??
ex) ??? ?? ???, ??? 30? ??? (?? ?? ???? ??? ??? ??)
??? ?????????? ??? ?????
V(s), N(s)? ??. S(s)? ?? ??
48. MC? ??
? ?c ? ? ? state? independent ??
? DP : ?hiI ? = ? ? ? ? ?` ?, ? [?(?, ?, ?`) + ??h ?` ]w`o
? MC : ? ?M ? ?M +
I
h
(?M ? ? ?M )
? MC do not bootstrap
? Computation independent of size of states ?
? ?? ?? state? ?? ?? state ? ?? ? ?? ?c ? ? ??? ??
? DP?? ?? ? ??
DP
1. all actions
2. only one transition
MC
1. sampled
2. to the end
49. MC? ??
? ?? State s? ???? ????, ??? V(s)? ??? ??? ??
????? ??? guarantee ? ? ???? ??
? ???, ??? ??? ?? ???? ???? ??? ?? s ? ? ????
????? ??? ?? ???? ??, ? ? ?? ? ? ? ? ? subset ??? ???
????? ??
50. ??
? MC methods?
? episode? ???? ?? ???
? Model-free: MDP transition? reward? ??? ??
? complete episode? ?? ???: no bootstrapping, ?? complete Return
? ?? ???? : ? ?
? = ?? Return
? ???:
? episodic MDP??? ? ? ??. episode? ???(terminate) ??? MC ??!
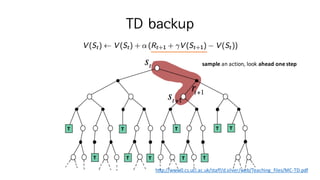
53. Temporal-Difference (TD) Learning
? TD methods
? ?? experience? ?? ??? (no use of experience memory)
? Model free: MDP trainsition / rewards ??? ?? ??
? DP?? estimate? ???? ?? (terminal ?? ??? ??) ?? ??
? MC? ?? bootstraping ??? ???? ??
? Guess? ?? Guess? ???? ?? (?? ????)
54. Temporal-Difference (TD) Learning
? ?? : ? ?
? ? ?? experience? ?? online?? ??
? Incremental every-visit MC
? ? ?M ? ?? return? ??? ?? ???? ??
? ? ?M ? ?M + ?(?? ? ? ?M )
? Simplest temporal-differnce learning algorithm: TD(0)
? ? ?M ? ??? return? RMiI + ?? ?M = immediate reward +
discounted value of next step
? ? ?M ? ?M + ?(? ?i? + ??(? ?i?) ? ? ?M )
TD target
TD error
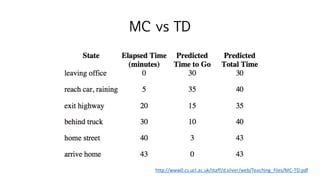
56. MC vs TD
? ??? ??? ??
? MC? ??
? ???? ??? ?? ??? ???. ?? = ?
? ????? trajectory ? ?, ? ?j?, , ? ??? ??? ? ? ??? ??? ??? ??
negative reward? ?? ??? ????? ???
? ??? ??? ? ???? negative ? ??? ???? ?? ? ??
? TD? ??
? ???? ??? ?? ????? ??? ??? ?. ? ? ?i? = ??
? ? ??? trajectory ? ?? negative reward? ???? ? ? ??
? ??? ??? ?? ?? ???? negative ? ??? ???? ?? ? ??
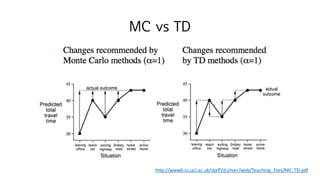
59. MC vs TD (1)
? TD? ??? return? ?? ?? ?? ? ??
? ? step ?? online?? ???
? MC? episode? ????? ??? ? ?? ??? ??
? TD? ??? return? ??? ?? ? ??
? TD? episode? ???? ??? (??? ???, ??? ????) ???
? MC? episode? ???? ???
? MC? episodic (terminating) environments??? ? ? ??
? TD? continuing (non-terminating) environments??? ? ? ??
60. Bias/Variance Trade-off
? Return : ?M = ?MiI + ??Mit + ? + ?KjI
?K. unbiased prediction of ? ?
? ?
? True TD target : RMiI + ??c
?MiI . unbiased prediction of ? ?
(? ?)
? TD target : ?MiI + ??h
?MiI . biased estimate of ? ?
(? ?)
? ?h
? ?? ??? ???? ?? (bias) ? ????
? ??? TD target? Return ?? ?? ?? variance? ???
? Return??? random action, transitions, reward? ???? episode? ?????
variance? ???
? TD target? ?? ??? random action, transition, reward? ?? ????
bias? ? ? ?? ????? ??
61. MC vs TD (2)
? MC : high variance, zero bias
? Good convergence property (even with function approximation)
? ?? ?? sensitive?? ??. ??? ?? ??? ?? bootstrap?? ?? ??
? TD : low variance, some bias
? ?? MC?? ?? efficient??
? TD(0)? ?c
?M ? converge??.
? ??? function approximation?? ?? converge?? ??? (??? specific? case)
? ???? ?? sensitive??
64. Batch MC & TD
? MC & TD? experiecne ???????? ?? ?h
(?) ?c
(?)
? ??? K?? ??? experience (batch solution)? ????
?I
I
, ?t
I
, ?-
I
, , ?K?
I
?I
?
, ?t
?
, ?-
?
, , ?K?
?
? ??? MC, TD(0)? ?????
67. Certainty Equivalence
?? data? ?? MDP? ???
? MDP? maximum likelihood? ?? ??
count of transition
mean rewards, divided by number of visit
only observe last return
68. MC & TD (3)
? TD? Markov property ? ???? ??
? TD? MDP? ??? ???? (Environment? state? ?? ??) ???
??
? ?? Markov environment?? ?? ?????
? MC? Markov property? ???? ?? ???
? ?? non-Markov environment?? ?? ?????
? ex) partially observable MDP
72. Bootstrapping & Sampling
? Bootstrapping : dont use real return
? MC does not bootstrap
? DP bootstrap : use estimate as a target
? TD bootstrap
? Sampling
? MC samples
? DP does not samples
? TD samples
http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/MC-TD.pdf
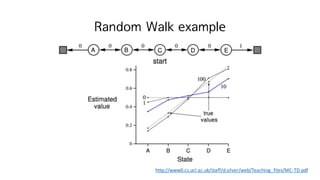
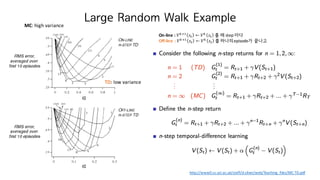
74. Large Random Walk Example
http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/MC-TD.pdf
MC: high variance
TD: low variance
On-line : ?hiI
?M ?h
?M ? ? step ??
Off-line : ?hiI
?M ?h
?M ? ???episode? ???
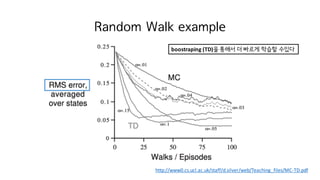
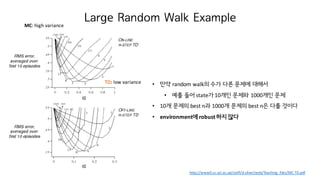
75. Large Random Walk Example
http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/MC-TD.pdf
MC: high variance
TD: low variance ? ?? random walk? ?? ?? ??? ???
? ?? ?? state? 10?? ??? 1000?? ??
? 10? ??? best n? 1000? ??? best n? ?? ???
? environment? robust ?? ??
76. Averaging n-step Returns
? ?M
()
= ?MiI + ??Mit + ?+ ?jI
?Mi + ?
?(?Mi)
? 1-step ? ?? 2-step ?? ??? n-step ??? ? ?? ????
? ?M
(t,?)
=
I
t
?M
(t)
+
I
t
?M
(?)
? ? ????? ??? ? ????
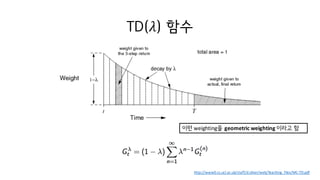
77. ? ? ??????
? ?? step? ?????? ?M
()
? ????? factor
? 1 ? ?? sum? 1? ????? normalizing factor
? ?M
?
= 1 ? ? ?jI
?M
()?
kI
? Forward-view TD(?)
? ? ?M = ? ?M + ? ?M
?
? ?(?M)
weighted sum of n-step returns
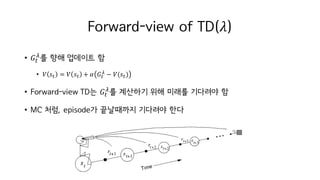
79. Forward-view of TD(?)
? ?M
?
? ?? ???? ?
? ? ?M = ? ?M + ? ?M
? ? ?(?M)
? Forward-view TD? ?M
?
? ???? ?? ??? ???? ?
? MC ??, episode? ????? ???? ??
80. Forward-view TD(?)
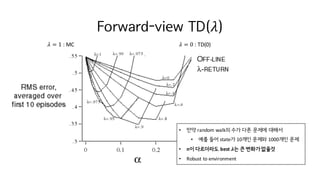
? = 1 : MC ? = 0 : TD(0)
? ?? random walk? ?? ?? ??? ???
? ?? ?? state? 10?? ??? 1000?? ??
? n? ????? best ?? ? ??? ???
? Robust to environment
81. Backward-view TD(?)
? Update online, every step, from incomplete sequences ? ??? ??
? ?? ??? ?????? ??? ?? ??? ??????
? Frequency heuristic : ?? ?? ???? state? importance?
? Recency heuristic : ?? ??? ??? state? importance?
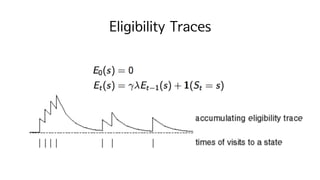
? Eligibility trace : ? ?? heuristic? ?? ?
83. Backward-view of TD(?)
? Eligibility trace? ?? state ? ? ?? ??
? ?(?)? ?? ? ? ?? ?????
?M = ?MiI + ?? ?MiI ? ? ?M
? ? ? ? + ??M ?M(?)
? Forward-view TD(?)
? ? ?M = ? ?M + ? ?M
?
? ?(?M)
: 1-step TD error
: multiply eligibility trace
84. TD(?) and TD(0)
? ? = 0? ?:
?M = ?MiI + ?? ?MiI ? ? ?M
?M ? = ?(?M = ?)
? ? ? ? + ??M ?M(?)
? ?? ??? ? ??? ??? ???. ? = 0? ?M = ?? ???? ? ??? ????? ??
? ?? = ?? ?????? ????
? ?? TD(0)? ???? ???.
? ? ? ? + ??M
![Reinforcement Learning:
?? ??? ?? ??? ???? ??? ??? ??
learner, decision maker
everything outside the agent
Policy ?? ? ? : ? ? [?, ?]](https://image.slidesharecdn.com/4-160714190818/85/Reinforcement-Learning-an-introduction-3-320.jpg)
![Optimal Value Functions
? Solving RL = finding an optimal policy
? ?? ? `?? ??? ?? ? ?? ? ?? ?? expected return? ?`?? ? ?
? ?c ? ?c`(?)
? ??
? = max
c
?c
?
? ??
?, ? = ???c ?c
(?, ?) : the expected return for taking action a in state s
? Express ??
in terms of ??
??
?, ? = ? ?h
?MihiI
KjM
hkH ?M = ?, ?M = ?
= ? ?MiI + ? ?hKjM
hkH ?Mihit ?M = ?, ?M = ?
= ? ?MiI + ? ??
(?MiI)|?M = ?, ?M = ?
= ?[?MiI + ? max
o`
? ?MiI, ?` |?M = ?, ?M = ?]](https://image.slidesharecdn.com/4-160714190818/85/Reinforcement-Learning-an-introduction-8-320.jpg)
![Bellman optimality equation
??
? = max
o
?[?MiI + ???
(?MiI)|?M = ?, ?M = ?]
= max
o
? ?` ?, ? [? ?, ?, ?` + ???
(?`)]w`
??
?, ? = ?[?MiI + ? max
o`
??
(?MiI, ?`)|?M = ?, ?M = ?]
= ? ?` ?, ? [? ?, ?, ?` + ? max
o`
??
?MiI, ?` ]w`
? For finite MDPs, Bellman optimality equation has a unique solution independent of the policy
? DP are obtained by turning Bellman equations into assignments
into update rules for improving approximations of value functions](https://image.slidesharecdn.com/4-160714190818/85/Reinforcement-Learning-an-introduction-10-320.jpg)
![Policy Evaluation
? How to compute ?c
? for an arbitrary policy ?? ? ? value? ?? ?? ???
= policy evaluation
?c
? = ? ?M + ??c
?` ?M = ?
= ? ? ? ? ? ? ?` ?, ? [?(?, ?, ?`) + ??c
?` ]
w`o
?? ?? ?? future reward? expectation](https://image.slidesharecdn.com/4-160714190818/85/Reinforcement-Learning-an-introduction-13-320.jpg)
![Policy Evaluation
? ?? environment? ?? ??? ?? ??? (known MDP)
?c
? ?? |?|?? unknown variables (Vc
? , ? ?)? ???
|?|?? linear equations
? ??? arbitrary approximate value function ? ?H??? ??. ?H, ?I, ?t,
?hiI ? = ? ?M + ??h ?` ?M = ?
= ? ? ? ? ? ? ?` ?, ? [?(?, ?, ?`) + ??h ?` ]
w`o
<Iterative policy evaluation>](https://image.slidesharecdn.com/4-160714190818/85/Reinforcement-Learning-an-introduction-14-320.jpg)
![Policy improvement theorem
? ??? policy? ??? ?? ??? ????
?c ?, ? = ?c ?M ?M = ?, ?M = ?
= ?c ?h ?MihiI
KjM
hkH ?M = ?, ?M = ?
= ?c ?MiI + ?h ?MihiI
KjM
hkI ?M = ?, ?M = ? = ?c ?MiI + ??c(?`) ?M = ?, ?M = ?
? ?c ?, ?`(?) ? ?c(?)?? ??? ?`? ??? ??
?c ?, ?`(?) ?c ? for all ? ? ??,
?c` ? ?c ? for all ? ?. WHY?
?? value??? ?`? ??? value
? ?
?, ? = ? ? ?` ?, ? [? ?, ?, ?` + ?max
o`
? ?
?MiI, ?` ]
w`](https://image.slidesharecdn.com/4-160714190818/85/Reinforcement-Learning-an-introduction-21-320.jpg)
![Greedy policy
?` ? = argmax
o
?c(?, ?)
= argmax
o
?[?MiI + ??c
?MiI |?M = ?, ?M = ?]
= argmax
o
? ?` ?, ? [?(?, ?, ?`) + ??c
?` ]w`
? Greedy policy ? ?c
??? ? + 1?? ??? value? ??? action? ??
<Policy improvement theorem>](https://image.slidesharecdn.com/4-160714190818/85/Reinforcement-Learning-an-introduction-26-320.jpg)
![MC? ??
? ?c ? ? ? state? independent ??
? DP : ?hiI ? = ? ? ? ? ?` ?, ? [?(?, ?, ?`) + ??h ?` ]w`o
? MC : ? ?M ? ?M +
I
h
(?M ? ? ?M )
? MC do not bootstrap
? Computation independent of size of states ?
? ?? ?? state? ?? ?? state ? ?? ? ?? ?c ? ? ??? ??
? DP?? ?? ? ??
DP
1. all actions
2. only one transition
MC
1. sampled
2. to the end](https://image.slidesharecdn.com/4-160714190818/85/Reinforcement-Learning-an-introduction-48-320.jpg)
