math. algebra
Download as PPT, PDF1 like809 views
The document contains examples of word problems involving rates, ratios, mixtures, as well as definitions and properties of linear inequalities, including the transitive, addition, and multiplication properties of inequalities, and examples of solving and graphing linear inequalities and their solution sets. The final part asks students to solve and graph the solution sets of several linear inequalities as seatwork.
1 of 24
Download to read offline




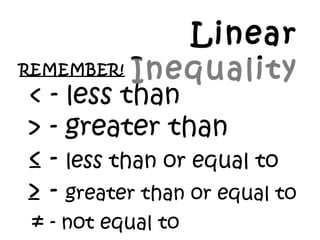





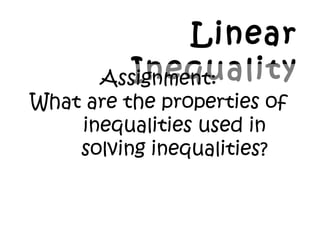



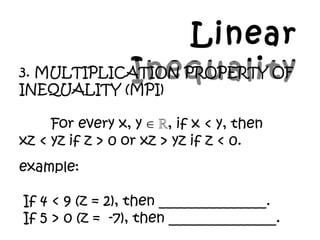


Recommended
Time & distance



Time & distanceHarmeet Singh
?
The document provides information on the relationships between distance, time, and speed. It includes formulas for converting between kilometers per hour and meters per second, calculating average speed when distances are covered at different speeds, and calculating relative speeds of objects like trains moving in the same or opposite directions. It then provides a quiz with 10 multiple choice questions related to using these formulas and concepts to solve word problems involving time, distance, and speed.GRE - Rates and Work



GRE - Rates and WorkGeorge Prep
?
This document provides an overview of topics related to rates and work, including distance, speed, and time; average speed; relative speed; to and fro motion; and work, time, and efficiency. It includes definitions and formulas for these concepts, as well as example problems and solutions. The document aims to teach the relationships between distance, speed, and time when motion is constant, how to calculate average speed, how to determine relative speeds of objects moving in the same or opposite directions, and how to solve word problems involving work completed over time by individuals or groups.17 chap



17 chapAnantha Bellary
?
1. The document provides examples and formulas for calculating time, distance, and speed. It includes the formulas for calculating speed, time, and distance when two quantities are given.
2. Sample problems are given involving calculating speeds and distances traveled by people and vehicles using the time-distance formulas. Distances, speeds, and times taken to cover distances are calculated in the examples.
3. Thirteen example problems are shown with step-by-step solutions for calculating speeds, times, and distances from trains, cyclists, thieves, and more using the time-distance formulas.Hoardings in Calicut - Outdoor Media across kozhikode



Hoardings in Calicut - Outdoor Media across kozhikodeOrganized Outdoor Options
?
To advertise across Kozhikode (Calicut) - 8860886720/9999163133/8826335802
Visit us at http://organizedoutdoor.com
TEDx Grenoble - City Open Data



TEDx Grenoble - City Open DataVasile Cotovanu
?
The document discusses open data related to public transit systems in various cities. It notes key statistics about train stations, track length, trains, and stops for Swiss Railways. It also provides similar statistics for Grenoble's public transit system, which includes 475 stations, 300 km of bus and tram tracks, and 3,000 vehicles with 77,000 stops daily. The presentation advocates that cities should make their public transit data openly available.Outdoor Hoardings across Kerala - Kerala Outdoor Media



Outdoor Hoardings across Kerala - Kerala Outdoor MediaOrganized Outdoor Options
?
To Advertise across Kerala State - 8860886720/9999163133/8826335802
Visit us at http://organizedoutdoor.com
The White Legacy--Generation 8, Chapter 1



The White Legacy--Generation 8, Chapter 1Keika20
?
Rhea gives birth to a baby boy named Spikenard, but calls him Spike. He is the first blonde-haired baby in the family tree. Meanwhile, Lewis celebrates making his 200th grilled cheese sandwich and Clary has her birthday party. However, the party goes late into the night, upsetting some of the pack members.Wynter Wonderland: Chapter 8



Wynter Wonderland: Chapter 8Keika20
?
Max lost his homework and is unsure where it went. Wynn asks Max about his missing homework. The chapter followed the lives of the sims in Wynter Wonderland, including the birth of Nina and Hazel moving out on her own as an adult. Landon is excited about being a new father to Nina despite just recently getting married and having his first child.Wynter Wonderland: Chapter 13



Wynter Wonderland: Chapter 13Keika20
?
The document provides an overview of events in the Kinsey household over time. Therese becomes a teenager and then moves out after her birthday. Wynn and Landon have more children, including daughters Valene, Westlyn, Xantha and son Ubert. The family celebrates various birthdays and milestones. Landon is promoted in his career while Wynn works towards completing her aspirations.Australia.travel english pptx



Australia.travel english pptxAkiraKi
?
The document introduces Australia by mentioning that the Sydney Opera House is a UNESCO World Heritage site, while noting that safety should be paid attention to around the Central Train Station and Kings Cross area in Sydney. It also notes that English is the language in Australia and a visa is required, and that sports like football and cricket can be watched year-round. Additionally, it provides travel information that there are no direct flights from Melbourne currently, and to switch to a domestic flight from other cities like with Qantas, Japan Airlines or Jetstar to arrive in Melbourne. Sights on the Great Ocean Road like the Twelve Apostles rock are also mentioned.Ppt about guru



Ppt about guruRamya Janakiraman
?
This document contrasts the roles of a teacher and a guru. It provides descriptions of a teacher in one line and a guru in the next, highlighting their differences. A teacher imparts knowledge and skills, while a guru facilitates personal growth and enlightenment. The guru challenges preconceptions and helps students find wisdom from within, rather than just instructing them.

Pr¨˘ctica 12 diapos



Pr¨˘ctica 12 diaposJoel Vera
?
The document discusses low-maintenance landscaping solutions for intermountain regions that face challenges like temperature extremes, short growing seasons, drying winds, and poor soil quality. It recommends approaches like xeriscaping, using windbreaks, amending soil, and planting native species to conserve water. These techniques can help landscapes better withstand hot/cold temperatures as well as periods of drought and deluge through strategies that reduce the need for irrigation while protecting against erosion.Content strategy: Getting your content to work for you



Content strategy: Getting your content to work for youContent That Clicks
?
What are the key things to consider when you're planning your content? From understanding your audience to measurement and optimisation, see how you can make your content work harder for you.presentation of meet



presentation of meetmeetrajput
?
This document discusses how communication is influenced by social and personal identity. It examines how individuals identify with groups and how this shapes interpersonal relationships, collective behavior, mass media consumption, and intercultural exchange. The document argues that communication is rarely done as truly independent individuals and that group membership is a fundamental part of human social interaction.Financial statements 3



Financial statements 3FaBEducation
?
Part three of FaBEducation.com's Financial Statements presentation on their active learning programme in business finance for non-financial managers and entrepreneurs Dinosaur



Dinosaurmeetrajput
?
The document is about a dinosaur. It states that the dinosaur discussed lives in North America and is an omnivore. Two website URLs are also included for more information.The White Legacy--Generation 4, Chapter 1



The White Legacy--Generation 4, Chapter 1Keika20
?
Callie has bought a new house that is brighter and less dark than her previous home. She has also been studying magic and joined a witch order. Jade has given birth to a daughter named Andromeda, who is the first child of Generation Five. The family is celebrating the new addition.Interactive Minds Summit 2013 Event Coverage



Interactive Minds Summit 2013 Event CoverageMichael Grierson
?
Social media analysis of the Interactive Minds Summit in Brisbane 1st of August 2013. This is a sample report prepared as part of BuzzNumbers' sponsorship of the event.My biography fabricio



My biography fabriciofabricio agurto
?
Mario Fabricio Agurto Guerrero was born on May 11, 1993 in Loja, Ecuador. He attended primary school in La Merced and high school at RUMI?AHUI, where he graduated with a specialty in mathematical physics. Agurto Guerrero loves his family, who have always supported him through good times and bad.The White Legacy--Generation 5, College (Part 1)



The White Legacy--Generation 5, College (Part 1)Keika20
?
Andromeda "Andi" White is the oldest of the Generation Five kids attending Sim State. She wants to major in drama despite her aunt wanting her to study biology. Andi goes on a date with Jonathan but isn't very interested in him. Her brother Hyde rolls the major of political science. Hyde is rescued from a dangerous situation by Andi and their cousin Lyra, who has just arrived at Sim State.Presentazione servizio WeLoadYou



Presentazione servizio WeLoadYouShipping Deals S.r.l.
?
La piattaforma WeLoadYou ¨¨ il modo innovativo di gestire le contrattazioni nel mondo delle spedizioni: il punto dˇŻincontro tra le Aziende che hanno necessit¨¤ di muovere merci e i Trasportatori.
Le Aziende e i Trasportatori possono gestire direttamente il proprio business senza intermediari, emettendo richieste e offerte di trasporto o attivando negoziazioni one-to-one.
Il sistema di notifiche integrato nel sito permette di essere aggiornati in tempo reale sulle risposte ricevute.
WeLoadYou ¨¨ un contenitore di informazioni e uno strumento di lavoro quotidiano che risponde allˇŻesigenza di avere un sistema di gestione domanda/offerta immediato e facilmente consultabile.
Gli operatori di settore potranno aumentare esponenzialmente i loro contatti, mentre le aziende risparmieranno tempo inviando contemporaneamente molteplici richieste di quotazione.Video palestin



Video palestinIZZAH YUSOFF
?
Video ini membandingkan kebahagiaan manusia dengan penderitaan anak-anak Palestina, dan mengungkapkan bahwa perusahaan tembakau Morris memberi sumbangan besar kepada Israel untuk membeli senjata yang digunakan melawan Palestina.Ballad of a mothers heart



Ballad of a mothers heartdjpprkut
?
A young man named Youth pleaded with his Maiden fair to prove his love for her. She asked him to bring her his mother's heart. Without hesitation, Youth took his mother's heart to give to his Maiden. As he ran back through the rain, Youth fell and was hurt, but still held his mother's heart. He then heard his mother's heart speak to him, asking if he was hurt.MAPEH - Volleyball



MAPEH - Volleyballdjpprkut
?
The libero is a defensive specialist position in volleyball introduced in 1999. The libero remains in the game at all times and is not limited by rotation rules. They usually replace the middle blocker in the back row and are responsible for passing serves and digging balls to keep rallies alive. Important attributes for a libero include being a good passer and digger. The setter is in charge of the offense and decides who to pass the ball to based on various factors like blocker positions. Key setter attributes include leadership, ball handling skills, consistency, communication, and quick decision making. Middle blockers strive to be involved in blocking anywhere on the court and look to hit quick sets. Important middle blocker traits are height, quickMore Related Content
Viewers also liked (20)
Wynter Wonderland: Chapter 8



Wynter Wonderland: Chapter 8Keika20
?
Max lost his homework and is unsure where it went. Wynn asks Max about his missing homework. The chapter followed the lives of the sims in Wynter Wonderland, including the birth of Nina and Hazel moving out on her own as an adult. Landon is excited about being a new father to Nina despite just recently getting married and having his first child.Wynter Wonderland: Chapter 13



Wynter Wonderland: Chapter 13Keika20
?
The document provides an overview of events in the Kinsey household over time. Therese becomes a teenager and then moves out after her birthday. Wynn and Landon have more children, including daughters Valene, Westlyn, Xantha and son Ubert. The family celebrates various birthdays and milestones. Landon is promoted in his career while Wynn works towards completing her aspirations.Australia.travel english pptx



Australia.travel english pptxAkiraKi
?
The document introduces Australia by mentioning that the Sydney Opera House is a UNESCO World Heritage site, while noting that safety should be paid attention to around the Central Train Station and Kings Cross area in Sydney. It also notes that English is the language in Australia and a visa is required, and that sports like football and cricket can be watched year-round. Additionally, it provides travel information that there are no direct flights from Melbourne currently, and to switch to a domestic flight from other cities like with Qantas, Japan Airlines or Jetstar to arrive in Melbourne. Sights on the Great Ocean Road like the Twelve Apostles rock are also mentioned.Ppt about guru



Ppt about guruRamya Janakiraman
?
This document contrasts the roles of a teacher and a guru. It provides descriptions of a teacher in one line and a guru in the next, highlighting their differences. A teacher imparts knowledge and skills, while a guru facilitates personal growth and enlightenment. The guru challenges preconceptions and helps students find wisdom from within, rather than just instructing them.

Pr¨˘ctica 12 diapos



Pr¨˘ctica 12 diaposJoel Vera
?
The document discusses low-maintenance landscaping solutions for intermountain regions that face challenges like temperature extremes, short growing seasons, drying winds, and poor soil quality. It recommends approaches like xeriscaping, using windbreaks, amending soil, and planting native species to conserve water. These techniques can help landscapes better withstand hot/cold temperatures as well as periods of drought and deluge through strategies that reduce the need for irrigation while protecting against erosion.Content strategy: Getting your content to work for you



Content strategy: Getting your content to work for youContent That Clicks
?
What are the key things to consider when you're planning your content? From understanding your audience to measurement and optimisation, see how you can make your content work harder for you.presentation of meet



presentation of meetmeetrajput
?
This document discusses how communication is influenced by social and personal identity. It examines how individuals identify with groups and how this shapes interpersonal relationships, collective behavior, mass media consumption, and intercultural exchange. The document argues that communication is rarely done as truly independent individuals and that group membership is a fundamental part of human social interaction.Financial statements 3



Financial statements 3FaBEducation
?
Part three of FaBEducation.com's Financial Statements presentation on their active learning programme in business finance for non-financial managers and entrepreneurs Dinosaur



Dinosaurmeetrajput
?
The document is about a dinosaur. It states that the dinosaur discussed lives in North America and is an omnivore. Two website URLs are also included for more information.The White Legacy--Generation 4, Chapter 1



The White Legacy--Generation 4, Chapter 1Keika20
?
Callie has bought a new house that is brighter and less dark than her previous home. She has also been studying magic and joined a witch order. Jade has given birth to a daughter named Andromeda, who is the first child of Generation Five. The family is celebrating the new addition.Interactive Minds Summit 2013 Event Coverage



Interactive Minds Summit 2013 Event CoverageMichael Grierson
?
Social media analysis of the Interactive Minds Summit in Brisbane 1st of August 2013. This is a sample report prepared as part of BuzzNumbers' sponsorship of the event.My biography fabricio



My biography fabriciofabricio agurto
?
Mario Fabricio Agurto Guerrero was born on May 11, 1993 in Loja, Ecuador. He attended primary school in La Merced and high school at RUMI?AHUI, where he graduated with a specialty in mathematical physics. Agurto Guerrero loves his family, who have always supported him through good times and bad.The White Legacy--Generation 5, College (Part 1)



The White Legacy--Generation 5, College (Part 1)Keika20
?
Andromeda "Andi" White is the oldest of the Generation Five kids attending Sim State. She wants to major in drama despite her aunt wanting her to study biology. Andi goes on a date with Jonathan but isn't very interested in him. Her brother Hyde rolls the major of political science. Hyde is rescued from a dangerous situation by Andi and their cousin Lyra, who has just arrived at Sim State.Presentazione servizio WeLoadYou



Presentazione servizio WeLoadYouShipping Deals S.r.l.
?
La piattaforma WeLoadYou ¨¨ il modo innovativo di gestire le contrattazioni nel mondo delle spedizioni: il punto dˇŻincontro tra le Aziende che hanno necessit¨¤ di muovere merci e i Trasportatori.
Le Aziende e i Trasportatori possono gestire direttamente il proprio business senza intermediari, emettendo richieste e offerte di trasporto o attivando negoziazioni one-to-one.
Il sistema di notifiche integrato nel sito permette di essere aggiornati in tempo reale sulle risposte ricevute.
WeLoadYou ¨¨ un contenitore di informazioni e uno strumento di lavoro quotidiano che risponde allˇŻesigenza di avere un sistema di gestione domanda/offerta immediato e facilmente consultabile.
Gli operatori di settore potranno aumentare esponenzialmente i loro contatti, mentre le aziende risparmieranno tempo inviando contemporaneamente molteplici richieste di quotazione.Video palestin



Video palestinIZZAH YUSOFF
?
Video ini membandingkan kebahagiaan manusia dengan penderitaan anak-anak Palestina, dan mengungkapkan bahwa perusahaan tembakau Morris memberi sumbangan besar kepada Israel untuk membeli senjata yang digunakan melawan Palestina.More from djpprkut (14)
Ballad of a mothers heart



Ballad of a mothers heartdjpprkut
?
A young man named Youth pleaded with his Maiden fair to prove his love for her. She asked him to bring her his mother's heart. Without hesitation, Youth took his mother's heart to give to his Maiden. As he ran back through the rain, Youth fell and was hurt, but still held his mother's heart. He then heard his mother's heart speak to him, asking if he was hurt.MAPEH - Volleyball



MAPEH - Volleyballdjpprkut
?
The libero is a defensive specialist position in volleyball introduced in 1999. The libero remains in the game at all times and is not limited by rotation rules. They usually replace the middle blocker in the back row and are responsible for passing serves and digging balls to keep rallies alive. Important attributes for a libero include being a good passer and digger. The setter is in charge of the offense and decides who to pass the ball to based on various factors like blocker positions. Key setter attributes include leadership, ball handling skills, consistency, communication, and quick decision making. Middle blockers strive to be involved in blocking anywhere on the court and look to hit quick sets. Important middle blocker traits are height, quickAtmosphere



Atmospheredjpprkut
?
The document summarizes key facts about Earth's atmosphere. It describes the composition of air, which is mostly nitrogen and oxygen. It also discusses the major divisions of the atmosphere based on temperature variations - the troposphere, stratosphere, and mesosphere. Additionally, it outlines how the atmosphere can be divided based on the distribution of gases, ozone and ions into the homosphere, heterosphere, ozonosphere, and ionosphere.TLE - Development of the circulation of money



TLE - Development of the circulation of moneydjpprkut
?
The document discusses the development of money and monetary systems throughout history. It begins with the barter system used in ancient times and the introduction of the first coins in Lydia. It then discusses the development of paper money in China and the largest banknote ever issued by the Philippines. The document also outlines the basic transactions between households and firms in an economy and some key macroeconomic concepts like unemployment, inflation, and economic growth. Finally, it discusses entrepreneurship and evaluating business opportunities based on factors like available markets, capital, skills, suppliers, manpower, and technology.III - resultant of non-concurrent forces



III - resultant of non-concurrent forcesdjpprkut
?
This document discusses calculating the resultant force of non-concurrent forces. It provides the equations to calculate the x and y components of the resultant force and the moment. It then provides examples of calculating the resultant force and point of application for different force systems acting on structures.on work by khalil gibran



on work by khalil gibrandjpprkut
?
This document provides an excerpt from Khalil Gibran's book "The Prophet" titled "On Work". The excerpt discusses work and the importance of doing work with love. It states that work allows one to participate in life's procession towards the infinite. When working with love, one binds themselves to others and to God. True work is love made visible. If work is done with distaste instead of joy, it is better to not work at all.TLE entepreneur



TLE entepreneurdjpprkut
?
The document discusses competencies required of effective entrepreneurs. It describes three clusters of personal entrepreneurial characteristics: achievement, planning, and power. It also discusses strengths and weaknesses of Filipino entrepreneurs, how to assess oneself as a potential entrepreneur, problems faced by entrepreneurs, and the importance of creativity, innovation, and management in entrepreneurial activities.HELE / TLEelectronics



HELE / TLEelectronicsdjpprkut
?
The document discusses various electronic components, including their schematic symbols and actual parts. It covers resistors, capacitors, semiconductors, transistors, switches, transformers, fuses, and more. It also discusses tools like the multimeter and how to measure voltage, current, resistance, and construct simple electronic projects. The document provides lessons on component symbols, diagrams, color coding, using a multimeter, and tips for building electronics projects.english - Tenses lesson



english - Tenses lessondjpprkut
?
This document provides information about different verb tenses in English including simple past, present, and future tenses, past and present progressive tenses, past perfect, present perfect, and future perfect tenses, and past perfect progressive and future perfect progressive tenses. For each tense, it provides the structure, examples of verbs in that tense form, and examples of sentences using that tense. It also includes tables comparing the different tenses across past, present, and future time frames and provides an exercise for labeling example sentences with the correct verb tense.biology.. kingdoms



biology.. kingdomsdjpprkut
?
- The document describes the key characteristics of 6 kingdoms - Bacteria, Archaea, Eukarya, Protista, Fungi, and Plantae. It discusses whether each kingdom has a nucleus, cell wall, ability to photosynthesize or fix nitrogen.
- Organisms are classified into kingdoms based on attributes like cell structure, ability to produce their own food, and whether they are single or multicellular.
- The kingdoms include unicellular lifeforms like bacteria and archaea, as well as multicellular eukaryotes like plants, fungi and animals.Recently uploaded (20)
Administrative bodies( D and C Act, 1940



Administrative bodies( D and C Act, 1940P.N.DESHMUKH
?
These presentation include information about administrative bodies such as D.T.A.B
CDL AND DCC, etc.Azure Administrator Interview Questions By ScholarHat



Azure Administrator Interview Questions By ScholarHatScholarhat
?
Azure Administrator Interview Questions By ScholarHatRRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)



RRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)SONU HEETSON
?
RRB ALP CBT 2 RAC Question Paper MCQ PDF Free Download. Railway Assistant Loco Pilot Mechanic Refrigeration and Air Conditioning Important Questions.Odoo 18 Accounting Access Rights - Odoo 18 şÝşÝߣs



Odoo 18 Accounting Access Rights - Odoo 18 şÝşÝߣsCeline George
?
In this slide, weˇŻll discuss on accounting access rights in odoo 18. To ensure data security and maintain confidentiality, Odoo provides a robust access rights system that allows administrators to control who can access and modify accounting data. Comprehensive Guide to Antibiotics & Beta-Lactam Antibiotics.pptx



Comprehensive Guide to Antibiotics & Beta-Lactam Antibiotics.pptxSamruddhi Khonde
?
? Comprehensive Guide to Antibiotics & Beta-Lactam Antibiotics
? Antibiotics have revolutionized medicine, playing a crucial role in combating bacterial infections. Among them, Beta-Lactam antibiotics remain the most widely used class due to their effectiveness against Gram-positive and Gram-negative bacteria. This guide provides a detailed overview of their history, classification, chemical structures, mode of action, resistance mechanisms, SAR, and clinical applications.
? What YouˇŻll Learn in This Presentation
? History & Evolution of Antibiotics
? Cell Wall Structure of Gram-Positive & Gram-Negative Bacteria
? Beta-Lactam Antibiotics: Classification & Subtypes
? Penicillins, Cephalosporins, Carbapenems & Monobactams
? Mode of Action (MOA) & Structure-Activity Relationship (SAR)
? Beta-Lactamase Inhibitors & Resistance Mechanisms
? Clinical Applications & Challenges.
? Why You Should Check This Out?
Essential for pharmacy, medical & life sciences students.
Provides insights into antibiotic resistance & pharmaceutical trends.
Useful for healthcare professionals & researchers in drug discovery.
? Swipe through & explore the world of antibiotics today!
? Like, Share & Follow for more in-depth pharma insights!Functional Muscle Testing of Facial Muscles.pdf



Functional Muscle Testing of Facial Muscles.pdfSamarHosni3
?
Functional Muscle Testing of Facial Muscles.pdfEntity Framework Interview Questions PDF By ScholarHat



Entity Framework Interview Questions PDF By ScholarHatScholarhat
?
Entity Framework Interview Questions PDF By ScholarHatMastering Soft Tissue Therapy & Sports Taping



Mastering Soft Tissue Therapy & Sports TapingKusal Goonewardena
?
Mastering Soft Tissue Therapy & Sports Taping: Pathway to Sports Medicine Excellence
This presentation was delivered in Colombo, Sri Lanka, at the Institute of Sports Medicine to an audience of sports physiotherapists, exercise scientists, athletic trainers, and healthcare professionals. Led by Kusal Goonewardena (PhD Candidate - Muscle Fatigue, APA Titled Sports & Exercise Physiotherapist) and Gayath Jayasinghe (Sports Scientist), the session provided comprehensive training on soft tissue assessment, treatment techniques, and essential sports taping methods.
Key topics covered:
? Soft Tissue Therapy ¨C The science behind muscle, fascia, and joint assessment for optimal treatment outcomes.
? Sports Taping Techniques ¨C Practical applications for injury prevention and rehabilitation, including ankle, knee, shoulder, thoracic, and cervical spine taping.
? Sports Trainer Level 1 Course by Sports Medicine Australia ¨C A gateway to professional development, career opportunities, and working in Australia.
This training mirrors the Elite Akademy Sports Medicine standards, ensuring evidence-based approaches to injury management and athlete care.
If you are a sports professional looking to enhance your clinical skills and open doors to global opportunities, this presentation is for you.Oral exam Kenneth Bech - What is the meaning of strategic fit?



Oral exam Kenneth Bech - What is the meaning of strategic fit?MIPLM
?
Presentation of the CEIPI DU IPBA oral exam of Kenneth Bech - What is the meaning of strategic fit? Dot NET Core Interview Questions PDF By ScholarHat



Dot NET Core Interview Questions PDF By ScholarHatScholarhat
?
Dot NET Core Interview Questions PDF By ScholarHatRRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)



RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)SONU HEETSON
?
RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper. MMV MCQ PDF Free Download for Railway Assistant Loco Pilot Exam.Inventory Reporting in Odoo 17 - Odoo 17 Inventory App



Inventory Reporting in Odoo 17 - Odoo 17 Inventory AppCeline George
?
This slide will helps us to efficiently create detailed reports of different records defined in its modules, both analytical and quantitative, with Odoo 17 ERP.How to Configure Proforma Invoice in Odoo 18 Sales



How to Configure Proforma Invoice in Odoo 18 SalesCeline George
?
In this slide, weˇŻll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.How to Configure Recurring Revenue in Odoo 17 CRM



How to Configure Recurring Revenue in Odoo 17 CRMCeline George
?
This slide will represent how to configure Recurring revenue. Recurring revenue are the income generated at a particular interval. Typically, the interval can be monthly, yearly, or we can customize the intervals for a product or service based on its subscription or contract. math. algebra
- 1. MATH
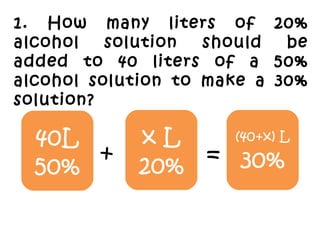
- 2. 1. How many liters of 20% alcohol solution should be added to 40 liters of a 50% alcohol solution to make a 30% solution? 40L 50% x L 20% (40+x) L 30%+ =
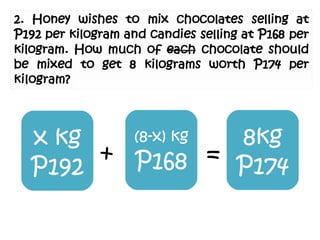
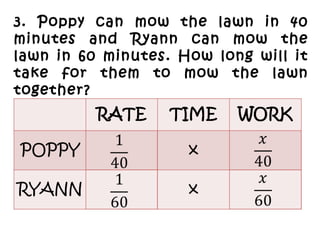
- 4. 3. Poppy can mow the lawn in 40 minutes and Ryann can mow the lawn in 60 minutes. How long will it take for them to mow the lawn together?
- 5. 4. An airplane which travels 180 miles per hour leaves the airport 8.5 hours after a ship sailed. If it overtakes the ship in 1 hour and 30 minutes, find the rate of the ship. RATE TIME DISTANCE Airplane 180mi/h 1.5h 1.5(180) Ship x 1.5h + 8.5h 10x
- 6. 5. A bus traveling at an average rate of?50?kilometers per hour made the trip to town in?6?hours. If it had traveled at?45?kilometers per hour, how many more minutes would it have taken to make the trip? RATE TIME DISTANCE A 50kph 6h 300km B 45kph 6h + x 45(6 + x)
- 7. Linear InequalityAn INEQUALITY is a mathematical statement which states that two quantities are not equal. TRICHOTOMY AXIOM For any numbers x and y, one and only one of the following is true: x < y x > y
- 8. Linear InequalityREMEMBER! < - less than > - greater than ˇÜ - less than or equal to ˇÝ - greater than or equal to ˇŮ - not equal to
- 9. When 3 is added to x, the sum remains larger than 9. Linear InequalityWhen you triple d and subtract 6, the result remains less than or equal to 15.
- 10. Linear Inequality Either s is greater than 8 or less than -8. t is greater than -1 but less than 5.
- 11. Linear Inequality REMEMBER! < or > ---------- ( parentheses ) ˇÜ or ˇÝ ----------
- 12. Linear Inequality x > 4 x ˇÝ 5 8 < x x ˇÝ 7 0 ˇÜ x < 5
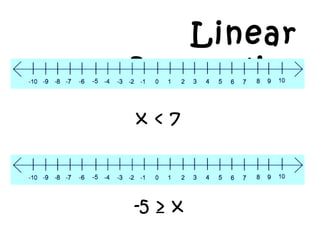
- 13. Linear Inequality x < 7 -5 ˇÝ x
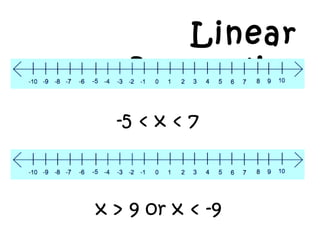
- 14. Linear Inequality -5 < x < 7 x > 9 or x < -9
- 17. Linear InequalityAssignment: What are the properties of inequalities used in solving inequalities?
- 18. Linear Inequality 1. TRANSITIVE PROPERTY OF INEQUALITY (TPI) 2. ADDITION PROPERTY OF INEQUALITY (API) 3. MULTIPLICATION PROPERTY OF INEQUALITY (MPI) Properties of Inequality
- 19. Linear Inequality1. TRANSITIVE PROPERTY OF INEQUALITY (TPI) For every x, y, and z , if x < y andˇĘ ? y < z, then x < z. example: If 4 < 9 and 9 < 10, then _______. If 5 > 0 and 0 > -5, then _______.
- 20. Linear Inequality2. ADDITION PROPERTY OF INEQUALITY (API) For every x, y and z, anyˇĘ ? number, if x < y, then x + z < y + z. example: If 4 < 9 (z = 2), then _______________. If 5 > 0 (z = -7), then _______________.
- 21. Linear Inequality3. MULTIPLICATION PROPERTY OF INEQUALITY (MPI) For every x, y , if x < y, thenˇĘ ? xz < yz if z > 0 or xz > yz if z < 0. example: If 4 < 9 (z = 2), then _______________. If 5 > 0 (z = -7), then _______________.
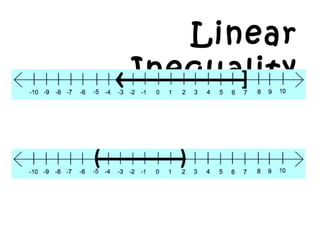
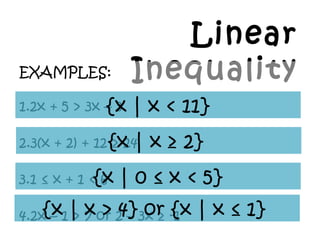
- 22. Linear InequalityEXAMPLES: 1.2x + 5 > 3x ¨C 3 2.3(x + 2) + 12 ˇÝ 24 3.1 ˇÜ x + 1 < 6 4.2x ¨C 1 > 7 or 2 ¨C 3x ˇÝ -1 {x | x < 11} {x | x ˇÝ 2} {x | 0 ˇÜ x < 5} {x | x > 4} or {x | x ˇÜ 1}
- 23. Linear InequalitySEATWORK: Solve and graph the solution set of each of the following inequalities. Get one whole sheet of paper. :)















