�ݺ�ߣ

Binary Trees Data Structures and Design in Java © Rick Mercer

Why Trees? Trees Tree Terminology Binary Trees One Recursive Tree Algorithm Outline

Storing Many Objects We have examined 2 major ways to store data in the main memory of the computer arrays use subscripts to immediately access elements fast access, but in the old days would consume more memory that you would like it to (not true anymore) linked structures each node refers to the next in the collection. To get to one you often traverse sequentially maybe slower, but maybe manages memory better

Another Linked Structure We now turn our attention to another major way of storing data: the Tree One implementation of a binary tree has nodes with a left and right link field 1 3 2 root edges nodes

First Some Definitions A tree has a set of nodes and directed edges that connect them a directed edge connects a parent to its children Tree properties one node is distinguished as the root every node (except the root) is connected by an edge from exactly one other node A unique path traverses from the root to each node

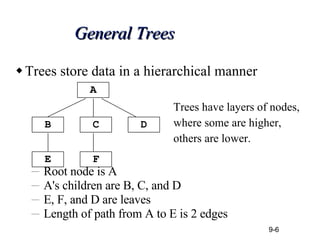
General Trees Trees store data in a hierarchical manner Root node is A A's children are B, C, and D E, F, and D are leaves Length of path from A to E is 2 edges A D B C F E Trees have layers of nodes, where some are higher, others are lower.

Some tree terminology Node An element in the tree references data and other nodes Root The node at the top It is upside down! Parent The node directly above another node (except root) Child The node(s) below a given node Size The number of descendants plus one for the node itself Leaves Nodes with no children Levels The root A is at level 0, E and F are at level 2

Applications of trees File Systems Hierarchical files systems include Unix and DOS In DOS, each represents an edge (In Unix, it's /) Each directory is a file with a list of all its children Store large volumes of data data can be quickly inserted, removed, and found Data structure used in a variety of situations implement data vase management systems compilers: expression tree, symbol tree The Computer Science Department's new logo okay we're working on a new logo A tree

Binary Trees N-ary tree has n children max from each node A binary tree is a tree where all nodes have zero, one or two children we'll study these binary trees only Each node is a leaf, has a right child, has a left child, or has both a left and right child A C B F D E

Binary Tree Defined A binary tree is either: an empty tree consists of a node, called a root, and zero, one, or two children (left and right), each of which are themselves binary trees This recursive definition uses the term "empty tree" as the base case Every non-empty node has two children, either of which may be empty On previous slide, C's left child is an empty tree.

Application: Expression Trees Binary trees can represent arithmetic expressions An infix expression will have a parent operator and two children operands: - 1 + 3 * The expression: ((3+(7*2))-1) Each parenthesized expression becomes a tree. Each operand is a leaf, each operator is an internal node 7 2

Evaluating the Expression tree To evaluate the expression tree: Take any two leaves Apply the parent's operator to them Replace that operator with the value of the subexpression. * 3 + 2 4 * 3 6 18

Huffman Coding Tree Binary trees in a famous file compression algorithm Huffman Coding Tree Each character is stored in a leaf The code is found by following the path 0 go left, 1 go right a is 01 e is 1 what is t? What is 0100100101 ? 'e' 't' 'a'

An inner class will be used to store one node of a binary tree private class BinaryTreeNode { // instance variables private Object data; private BinaryTreeNode left; private BinaryTreeNode right; BinaryTreeNode() // This would be given to us { data = null; left = null; right = null; }

A Third Constructor BinaryTreeNode(Object theData) { // Used most often data = theData; left = null; right = null; } BinaryTreeNode(Object theData, BinaryTreeNode leftLink, BinaryTreeNode rightLink) { data = theData; left = leftLink; right = rightLink; } } // end class BinaryTreeNode

class BinaryTreeNode Each BinaryTreeNode object has a reference to an object object so we can store anything a link to the left subtree which could be an empty tree a link to the right subtree which could be an empty tree 3 Constructors two set some data fields to null ( left and right ) The data fields are private Like LinkNode , methods in the enclosing class can reference private instance variables of the inner class

Build a Tree with Three Nodes Hard code a tree referenced by root We do not yet have a nice way to insert new nodes This demonstrates linked BinaryTreeNode objects BinaryTreeNode root = new BinaryTreeNode("1"); root.left = new BinaryTreeNode("2"); root.right = new BinaryTreeNode("3"); "1" "3" "2" root

Recursion and Trees Trees are defined recursively and tree algorithms are implemented recursively For example, size (all descendants plus 1) // call a size after building a tree System.out.println(size(root)); public int size(BinaryTreeNode t) { // return size of tree rooted at t What is the base case? (think simplest possibility) With trees, the recursive case often makes a recursive call on the left subtree and another on the right subtree }

Active Learning 1) Draw this tree BinaryTreeNode aTree = new BinaryTreeNode("1"); aTree.left = new BinaryTreeNode("2"); aTree.right = new BinaryTreeNode("3"); aTree.right.right = new BinaryTreeNode("4"); aTree.right.left = new BinaryTreeNode("5"); aTree.left.right = new BinaryTreeNode("6"); aTree.left.left = new BinaryTreeNode("7"); aTree.left.left.left = new BinaryTreeNode("8"); 2) Then write output generated System.out.println(size(aTree)); // Of course you could keep track of // size as another instance variable

�ݺ�ߣ

Trees - Data structures in C/Java

More Related Content

Trees - Data structures in C/Java