Esercitazioni di statistica 8/10
0 likes231 views
Il documento presenta esercizi di statistica riguardanti il calcolo degli errori e dei limiti di confidenza per la didattica e la qualit dei materiali. Inoltre, si discute il test delle ipotesi per verificare la legittimit delle certificazioni di resistenza dei materiali e le conseguenze di sostanze tossiche sulla crescita delle piante. Vengono utilizzati concetti statistici come il teorema del limite centrale e la distribuzione t per stimare le medie e la veridicit delle affermazioni.
![1. Stimare, con 留 =5%, lintervallo di confidenza dellaltezza media di una variet di
pomodoro, attraverso esemplari alti 22, 25, 21, 23, 24, 25, 21 pollici.
La stima dei limiti fiduciali va effettuata attraverso la distribuzione di t, dal momento che la deviazione standard della
popolazione (s) 竪 ignota. La formula per calcolare i limiti fiduciali 竪 simile in tutto a quella utilizzata con Z:
亮 = 賊 t*E.S. + xmedio
dove t: valore tabulato per il livello di errore desiderato e per i GRADI DI LIBERTA del campione (n-1) 1
ES: errore standard (deviazione standard della distribuzione delle medie campionarie)= (s/radice[n])
xmedio: stimatore di 亮..
Calcolo della deviazione standard campionaria:
x x-xmedio (x-xmedio)2
22 -1 1
25 2 4
21 -2 4
23 0 0
24 1 1
25 2 4
21 -2 4
Media 23
GL 6
SS devianza 18 somma (x-xmedio)2
s2
varianza 3 SS / GL
s dev.st. 1.73 radice (s2
)
ES errore st. 0.65 s /radice(n)
Valore di t tabulato per 留 = 0.05 e GL = 6: 2.44
Limiteinf = - t*E.S. + xmedio = 21.414 pollici
Limitesup = + t*E.S. + xmedio = 24.586 pollici
Lintervallo fiduciale pu嘆 essere espresso attraverso i suoi due limiti o come differenza tra questi (=3.172 pollici).
1
Esiste una intera famiglia di distribuzioni t, una per ogni grado di libert.](https://image.slidesharecdn.com/sostegno19022008-170630105114/85/Esercitazioni-di-statistica-8-10-26-320.jpg)
![4. In un vivaio sono coltivate pianticelle di ciliegio per legname di pregio; dopo due mesi dalla
semina questa specie raggiunge unaltezza media di 25 centimetri ( = 1.7 cm). A causa di un
incidente, su quel terreno sono state disperse sostanze tossiche. Per una verifica dei loro
potenziali effetti negativi sulla crescita delle piantine vengono seminate sul terreno inquinato
7 pianticelle che, controllate dopo 2 mesi, raggiungono unaltezza media di 23 cm. Si pu嘆
sostenere che le sostanze tossiche disperse inibiscano la crescita delle piantine?
Per verificare lipotesi relativa alla media xmedio di un campione rispetto ad una media attesa 亮, si pu嘆 ricorrere alla
distribuzione normale standardizzata in questo caso la distribuzione di Z poich辿 竪 nota. Al fine di verificare che
leffetto dellinquinante sia reale e che la variazione di altezza rilevata non sia dovuta solamente al caso
(campionamento effettuato in una coda della distribuzione normale), occorre valutare se la media della popolazione 袖
da cui 竪 estratto il campione (ciliegi su terreno inquinato) 竪 statisticamente minore di quella attesa 袖0 (piantine di
ciliegio in genere).
IPOTESI NULLA: H0 : xmedio 袖
IPOTESI ALTERNATIVA: H1 : xmedio < 袖
Scelgo di effettuare un test A UNA CODA: poich辿 il testo del problema specifica gi qual 竪 la direzione delleffetto
dellinquinante (solo negativo) posso considerare solo una parte della distribuzione normale (quella a sinistra poich辿
la media del campione 竪 minore di quella della popolazione).2
Se lipotesi nulla 竪 vera, le 7 piantine del campione appartengono alla popolazione con media 25 cm e deviazione
standard 1.7; occorre determinare se la probabilit che il campione appartenga a questa popolazione (= area sottesa
alla distribuzione di Z) sia troppo piccola per accettare questa ipotesi.
亮 = 25 cm
= 1.7 cm
xmedio = 23 cm
n = 7
Z = (xmedio 亮) /ES NB: la distribuzione 竪 sempre delle medie campionarie (tra le medie derivanti da
tutti i possibili campioni di 7 piantine di ciliegio ne scelgo una), quindi occorre
usare ES.
Z = (23-25) / (1.7/ radice[7]) = -3.11 Z CALCOLATO
Z = 1.645 Z TABULATO (livello di confidenza del 95%, si esclude una probabilit del 5% in una coda)
Z = 2.3267 Z TABULATO (livello di confidenza del 99%, calcolo per interpolazione)
I valori di Z tabulati, da considerare negativi poich辿 sappiamo di essere nella coda sinistra, individuano il limite della
ZONA DI ACCETTAZIONE DELLIPOTESI NULLA: se Z calcolato cade oltre tale zona, le probabilit associate al
suo dato sono troppo piccole per accettare di trovarsi davanti ad ununica popolazione, e lipotesi nulla pertanto 竪
rifiutata. Linquinate ha cio竪 avuto un effetto ALTAMENTE SIGNIFICATIVO (livello di errore minore di 0.01).
2
Un test 竪 unilaterale o a una coda, quando il ricercatore si chiede se una media 竪 maggiore dell'altra, escludendo a priori che essa possa essere
minore. Un test 竪 bilaterale o a due code, quando il ricercatore si chiede se tra le due medie esista una differenza significativa, senza che egli abbia
indicazioni su quali sia la maggiore o la minore.
ZONA DI RIFIUTO
ZONA DI
ACCETTAZIONE
-2.3267 (test a una coda, coda sx)
ZONA DI RIFIUTO
ZONA DI
ACCETTAZIONE
-1.645 (test a una coda, coda sx)
-3.11 (Z CALCOLATO)
-3.11 (Z CALCOLATO)](https://image.slidesharecdn.com/sostegno19022008-170630105114/85/Esercitazioni-di-statistica-8-10-28-320.jpg)
Esercitazioni di statistica 8/10
- 1. Corso di Statistica Lezioni di sostegno A.A. 2006-2007 Docente: Dott. Giorgio VACCHIANO Dip. AgroSelviTer_ Sez. Selvicoltura giorgio.vacchiano@unito.it Universit degli Studi di Torino
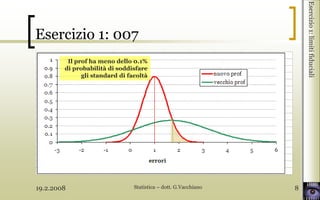
- 2. 19.2.2008 Statistica dott. G.Vacchiano 2 Esercizio 1: 007 Per controllare la qualit dellinsegnamento, il preside fa spiare il professore di statistica in 7 lezioni successive, e annota quante volte il prof sbaglia una spiegazione: Lezione I II III IV V VI VII Errori 3 1 1 0 5 2 0 Sapendo che il prof ogni tanto si sveglia male ( = 1.5), calcolare il numero minimo e massimo di errori (distribuiti normalmente) atteso nel 95% dei casi. Esercizio1:limitifiduciali
- 3. 19.2.2008 Statistica dott. G.Vacchiano 3 Esercizio1:limitifiduciali TEOREMA DEL LIMITE CENTRALE: La media delle medie campionarie 竪 uno stimatore esatto della media della popolazione. Se voglio stimare da UN SOLO campione, commetter嘆 un errore. La media reale sar racchiusa in un intervallo fiduciale (o di confidenza). Esercizio 1: 007
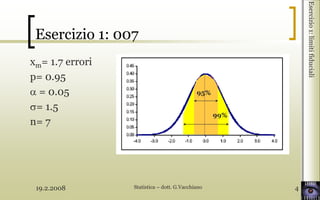
- 4. 19.2.2008 Statistica dott. G.Vacchiano 4 Esercizio1:limitifiduciali xm= 1.7 errori p= 0.95 = 0.05 = 1.5 n= 7 Esercizio 1: 007 99% 95%
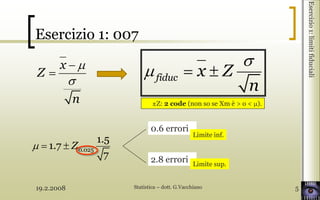
- 5. 19.2.2008 Statistica dott. G.Vacchiano 5 Esercizio1:limitifiduciali Esercizio 1: 007 x Z n fiduc x Z n 0.025 1.5 1.7 7 Z 0.6 errori 2.8 errori Limite sup. Limite inf. 賊Z: 2 code (non so se Xm 竪 > o < ).
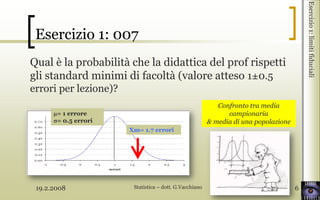
- 6. 19.2.2008 Statistica dott. G.Vacchiano 6 Esercizio 1: 007 Qual 竪 la probabilit che la didattica del prof rispetti gli standard minimi di facolt (valore atteso 1賊0.5 errori per lezione)? Esercizio1:limitifiduciali = 1 errore = 0.5 errori Xm= 1.7 errori Confronto tra media campionaria & media di una popolazione
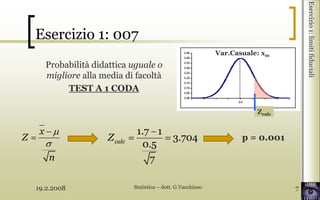
- 7. 19.2.2008 Statistica dott. G.Vacchiano 7 Esercizio1:limitifiduciali Probabilit didattica uguale o migliore alla media di facolt TEST A 1 CODA Var.Casuale: xm 1.7 1 3.704 0.5 7 calcZ Esercizio 1: 007 Zcalc x Z n p = 0.001
- 8. 19.2.2008 Statistica dott. G.Vacchiano 8 Il prof ha meno dello 0.1% di probabilit di soddisfare gli standard di facolt Esercizio 1: 007 Esercizio1:limitifiduciali
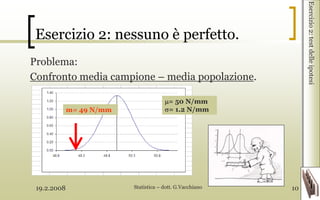
- 9. 19.2.2008 Statistica dott. G.Vacchiano 9 Esercizio 2: nessuno 竪 perfetto La ditta ACME fornisce tondini di ferro per cemento armato. Il tondino 竪 certificato per una resistenza media a trazione di 50 N/mm ( =1.2). In 6 casi di incidente in cui il materiale era stato usato per realizzare opere di contenimento, il tondino ha ceduto ai seguenti valori di trazione: N/cm 470 482 490 517 547 434 Si pu嘆 affermare che la ACME ha rilasciato una certificazione truffaldina? Esercizio2:testdelleipotesi
- 10. 19.2.2008 Statistica dott. G.Vacchiano 10 Esercizio 2: nessuno 竪 perfetto. Problema: Confronto media campione media popolazione. Esercizio2:testdelleipotesi = 50 N/mm = 1.2 N/mmm= 49 N/mm
- 11. 19.2.2008 Statistica dott. G.Vacchiano 11 Esercizio 2: nessuno 竪 perfetto Soluzione: Test delle ipotesi IPOTESI ZERO (nulla): la media del campione 竪 solo casualmente minore di quella della pop. (errore di campionamento). IPOTESI ALTERNATIVA: La media del campione 竪 significativamente minore di quella della popolazione (truffa in vista!!). Esercizio2:testdelleipotesi
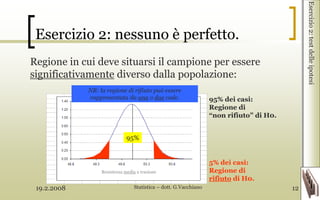
- 12. 19.2.2008 Statistica dott. G.Vacchiano 12 Esercizio 2: nessuno 竪 perfetto. Regione in cui deve situarsi il campione per essere significativamente diverso dalla popolazione: Esercizio2:testdelleipotesi 95% dei casi: Regione di non rifiuto di H0. 5% dei casi: Regione di rifiuto di H0. 95% NB: la regione di rifiuto pu嘆 essere rappresentata da una o due code. Resistenza media a trazione
- 13. 19.2.2008 Statistica dott. G.Vacchiano 13 Esercizio 2: nessuno 竪 perfetto. Esercizio2:testdelleipotesi Nulla in statistica (e in scienza) pu嘆 mai essere accettato. Lobiettivo 竪 falsificare.
- 14. 19.2.2008 Statistica dott. G.Vacchiano 14 Esercizio 2: nessuno 竪 perfetto. Se il verificarsi di quella media campionaria 竪 raro, 竪 probabile che il campione appartenga ad una popolazione diversa. Esercizio2:testdelleipotesi Tondino certificato Tondino truffaldino γ pi湛 probabile che la media campionaria appartenga alluna o allaltra popolazione?
- 15. 19.2.2008 Statistica dott. G.Vacchiano 15 Esercizio 2: nessuno 竪 perfetto. 1. Confronto i valori-soglia. Sospetto che il tondino sia pi湛 debole, considero quindi solo una coda. ptest=0.95 test=0.05 Ztest=-1.645 Esercizio2:testdelleipotesi p49 50 2.041 1.2 6 calcZ SE NB: una sola coda > la truffa 竪 ragionevole solo per valori inferiori a quelli certificati (non superiori!!).
- 16. 19.2.2008 Statistica dott. G.Vacchiano 16 Esercizio 2: nessuno 竪 perfetto. 2. Oppure, confronto le probabilit associate ptest=0.95 calc=0.05 pcalc=0.979 calc=0.021 Esercizio2:testdelleipotesi p 49 50 2.041 1.2 6 calcZ
- 17. 19.2.2008 Statistica dott. G.Vacchiano 17 Esercizio 2: nessuno 竪 perfetto. LA REGOLA MADRE: pcalc<ptest: rifiuto H0 |Zcalc|>|Ztab|: rifiuto H0 pcalc>ptest: non rifiuto H0 |Zcalc|<|Ztab|: non rifiuto H0 Esercizio2:testdelleipotesi Sono stato truffato!
- 18. 19.2.2008 Statistica dott. G.Vacchiano 18 Esercizio3:distribuzionedit
- 19. 19.2.2008 Statistica dott. G.Vacchiano 19 Esercizio3:distribuzionedit
- 20. 19.2.2008 Statistica dott. G.Vacchiano 20 Esercizio3:distribuzionedit
- 21. 19.2.2008 Statistica dott. G.Vacchiano 21 Esercizio3:distribuzionedit 1899: Birraio capo Guinness Brewery Dublin (EIRE)
- 22. 19.2.2008 Statistica dott. G.Vacchiano 22 Esercizio3:distribuzionedit IPOTESI NULLA IPOTESI ALTERNATIVA x t s n
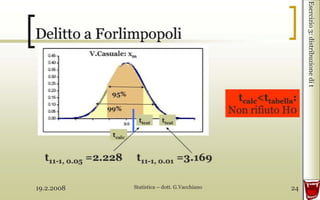
- 23. 19.2.2008 Statistica dott. G.Vacchiano 23 Esercizio3:distribuzionedit Valori di t Gradidilibert significativit
- 24. 19.2.2008 Statistica dott. G.Vacchiano 24 Esercizio3:distribuzionedit
- 25. Simulazione di esame 19.2.2008 Statistica dott. G.Vacchiano 25 WOW. IN QUESTO COMPITO NON CE UN ERRORE. QUALCUNO HA CAPITO TUTTO! FINALMENTE ! DA NON CRE E LA LISTA DELLE RISPOSTE. LHO SCRITTA IO.
- 26. 1. Stimare, con 留 =5%, lintervallo di confidenza dellaltezza media di una variet di pomodoro, attraverso esemplari alti 22, 25, 21, 23, 24, 25, 21 pollici. La stima dei limiti fiduciali va effettuata attraverso la distribuzione di t, dal momento che la deviazione standard della popolazione (s) 竪 ignota. La formula per calcolare i limiti fiduciali 竪 simile in tutto a quella utilizzata con Z: 亮 = 賊 t*E.S. + xmedio dove t: valore tabulato per il livello di errore desiderato e per i GRADI DI LIBERTA del campione (n-1) 1 ES: errore standard (deviazione standard della distribuzione delle medie campionarie)= (s/radice[n]) xmedio: stimatore di 亮.. Calcolo della deviazione standard campionaria: x x-xmedio (x-xmedio)2 22 -1 1 25 2 4 21 -2 4 23 0 0 24 1 1 25 2 4 21 -2 4 Media 23 GL 6 SS devianza 18 somma (x-xmedio)2 s2 varianza 3 SS / GL s dev.st. 1.73 radice (s2 ) ES errore st. 0.65 s /radice(n) Valore di t tabulato per 留 = 0.05 e GL = 6: 2.44 Limiteinf = - t*E.S. + xmedio = 21.414 pollici Limitesup = + t*E.S. + xmedio = 24.586 pollici Lintervallo fiduciale pu嘆 essere espresso attraverso i suoi due limiti o come differenza tra questi (=3.172 pollici). 1 Esiste una intera famiglia di distribuzioni t, una per ogni grado di libert.
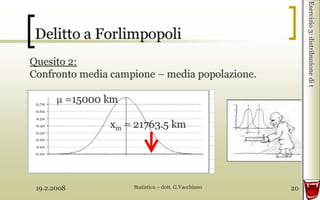
- 27. 3. Da una fornitura di 1000 pali di castagno per viticoltura si estrae un campione di 20 elementi per un controllo della qualit. La densit del legno misurata nei 20 pali 竪 riportata nella tabella seguente: id id 1 .681 11 .681 2 .654 12 .654 3 .630 13 .630 4 .460 14 .460 5 .690 15 .690 6 .672 16 .672 7 .693 17 .693 8 .701 18 .701 9 .725 19 .725 10 .697 20 .697 Calcolare i limiti fiduciari della densit media della fornitura di pali con un livello di confidenza del 95%. Valore di t tabulato per 留 =0.05 e GL =19: 2.093 Limiteinf = - t*E.S. + xmedio = 0.626 kg/dm3 Limitesup = + t*E.S. + xmedio = 0.695 kg/dm3 x x-xmedio (x-xmedio)2 0.681 0.0207 0.0004 0.654 -0.0063 0.00004 0.63 -0.0303 0.0009 0.46 -0.2003 0.0401 0.69 0.0297 0.0009 0.672 0.0117 0.0001 0.693 0.0327 0.0011 0.701 0.0407 0.0017 0.725 0.0647 0.0042 0.697 0.0367 0.0013 0.681 0.0207 0.0004 0.654 -0.0063 0.00004 0.63 -0.0303 0.0009 0.46 -0.2003 0.0401 0.69 0.0297 0.0009 0.672 0.0117 0.0001 0.693 0.0327 0.0011 0.701 0.0407 0.0017 0.725 0.0647 0.0042 0.697 0.0367 0.0013 Media 0.6603 GL 19 SS devianza 0.1016 somma (x-xmedio)2 s2 varianza 0.0053 SS / GL s dev.st. 0.0731 radice (s2 ) ES errore st. 0.0163 s /radice(n)
- 28. 4. In un vivaio sono coltivate pianticelle di ciliegio per legname di pregio; dopo due mesi dalla semina questa specie raggiunge unaltezza media di 25 centimetri ( = 1.7 cm). A causa di un incidente, su quel terreno sono state disperse sostanze tossiche. Per una verifica dei loro potenziali effetti negativi sulla crescita delle piantine vengono seminate sul terreno inquinato 7 pianticelle che, controllate dopo 2 mesi, raggiungono unaltezza media di 23 cm. Si pu嘆 sostenere che le sostanze tossiche disperse inibiscano la crescita delle piantine? Per verificare lipotesi relativa alla media xmedio di un campione rispetto ad una media attesa 亮, si pu嘆 ricorrere alla distribuzione normale standardizzata in questo caso la distribuzione di Z poich辿 竪 nota. Al fine di verificare che leffetto dellinquinante sia reale e che la variazione di altezza rilevata non sia dovuta solamente al caso (campionamento effettuato in una coda della distribuzione normale), occorre valutare se la media della popolazione 袖 da cui 竪 estratto il campione (ciliegi su terreno inquinato) 竪 statisticamente minore di quella attesa 袖0 (piantine di ciliegio in genere). IPOTESI NULLA: H0 : xmedio 袖 IPOTESI ALTERNATIVA: H1 : xmedio < 袖 Scelgo di effettuare un test A UNA CODA: poich辿 il testo del problema specifica gi qual 竪 la direzione delleffetto dellinquinante (solo negativo) posso considerare solo una parte della distribuzione normale (quella a sinistra poich辿 la media del campione 竪 minore di quella della popolazione).2 Se lipotesi nulla 竪 vera, le 7 piantine del campione appartengono alla popolazione con media 25 cm e deviazione standard 1.7; occorre determinare se la probabilit che il campione appartenga a questa popolazione (= area sottesa alla distribuzione di Z) sia troppo piccola per accettare questa ipotesi. 亮 = 25 cm = 1.7 cm xmedio = 23 cm n = 7 Z = (xmedio 亮) /ES NB: la distribuzione 竪 sempre delle medie campionarie (tra le medie derivanti da tutti i possibili campioni di 7 piantine di ciliegio ne scelgo una), quindi occorre usare ES. Z = (23-25) / (1.7/ radice[7]) = -3.11 Z CALCOLATO Z = 1.645 Z TABULATO (livello di confidenza del 95%, si esclude una probabilit del 5% in una coda) Z = 2.3267 Z TABULATO (livello di confidenza del 99%, calcolo per interpolazione) I valori di Z tabulati, da considerare negativi poich辿 sappiamo di essere nella coda sinistra, individuano il limite della ZONA DI ACCETTAZIONE DELLIPOTESI NULLA: se Z calcolato cade oltre tale zona, le probabilit associate al suo dato sono troppo piccole per accettare di trovarsi davanti ad ununica popolazione, e lipotesi nulla pertanto 竪 rifiutata. Linquinate ha cio竪 avuto un effetto ALTAMENTE SIGNIFICATIVO (livello di errore minore di 0.01). 2 Un test 竪 unilaterale o a una coda, quando il ricercatore si chiede se una media 竪 maggiore dell'altra, escludendo a priori che essa possa essere minore. Un test 竪 bilaterale o a due code, quando il ricercatore si chiede se tra le due medie esista una differenza significativa, senza che egli abbia indicazioni su quali sia la maggiore o la minore. ZONA DI RIFIUTO ZONA DI ACCETTAZIONE -2.3267 (test a una coda, coda sx) ZONA DI RIFIUTO ZONA DI ACCETTAZIONE -1.645 (test a una coda, coda sx) -3.11 (Z CALCOLATO) -3.11 (Z CALCOLATO)