mathematical model
Download as pptx, pdf12 likes15,371 views
The document presents an overview of mathematical models. It defines mathematical models as mathematical descriptions of real situations that make assumptions and simplifications about reality. There are three main types of models: linear, quadratic, and exponential models. The document discusses how to develop a mathematical model by comparing model predictions to real data. It provides an example of a differential equation model of the spread of a contagious flu.
mathematical model
- 1. MATHEMATICAL MODELpresentedBY: KATHERINE SILVANUMERICAL MOTHODS IN PETROLEUM ENGINEERINGimage 1Source: www.emi s.de/.../NNJ/images_number1/MGC-05.jpg
- 2. DEFINITIONA mathematical model is the mathematical description of a real situation.In developing the model, some assumptions are made and we consider some simplifications of reality.A model can represent it using: Relations
- 3. functionsTYPES OF MODELSThere are three types of models:Linear model: We call linear models to situations can be represented by a linear function. can be determined graphically or by means of an equation.images 2 and 3Source: http://entren.dgsca.unam.mx/ModMat/mm05.html
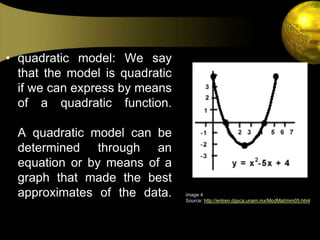
- 4. quadratic model: We say that the model is quadratic if we can express by means of a quadratic function. A quadratic model can be determined through an equation or by means of a graph that made the best approximates of the data. image 4Source: http://entren.dgsca.unam.mx/ModMat/mm05.html
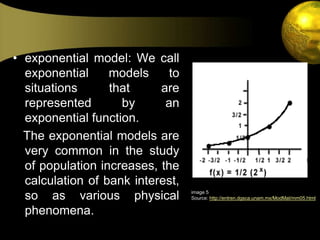
- 5. exponential model: We call exponential models to situations that are represented by an exponential function. The exponential models are very common in the study of population increases, the calculation of bank interest, so as various physical phenomena.image 5Source: http://entren.dgsca.unam.mx/ModMat/mm05.html
- 6. HOW DO YOU DEVELOP A MATHEMATICAL MODEL?The process for develop a mathematical model is as following: 4.Compare the data obtained as predictions with real data. If the data are different, the process is restarted.
- 7. DIFFERENTIAL EQUATIONS AS MATHEMATICAL MODEL A single differential equation mathematical model can be of many different phenomena. a mathematical model is formed by an initial value problem, or also value problem at the border.image 6Source: http://entren.dgsca.unam.mx/ModMat/mm05.html
- 8. EXAMPLE OF MATHEMATICAL MODELAn analysis of the spread of a contagious flu, for example, is reasonable to assume that the rate or reason that spreads not only is proportional to the number of people, x (t), which have contracted at time t, but also the number of subjects, and (t), which have not yet been exposed to infection. If the rate is dx / dt, thenWhere k is the usual constant of proportionality.
- 9. If, for example, introduces an infected person in a constant population of n people, then x and y are related by x + y = n + 1. We use this equation to eliminate and in equation (1) and obtain the model?An obvious initial condition accompanying equation (2) is x (0) = 1.