More Related Content Viewers also liked (19) PDF
Cómo hacer un sitio Web fácil, rápido y en forma económica con Wordpress
Pablo Capurro ?
PDF
Estrategia y metodología para Contenidos Interactivos
Pablo Capurro ?
PDF
КОМПЛЕКТ ПЛАНАХРОМАТИЧЕСКИХ МИКРООБЪЕКТИВОВ С ПОСТОЯННЫМ ПОЛОЖЕНИЕМ ЗРАЧКОВ
ITMO University ?
Similar to 进化计算シンホ?シ?ウム200712 (11)
PDF
[読会]Long tail learning via logit adjustment
shima o ?
PDF
クラスタリングとレコメンデーション资料
洋資 堅田 ?
More from Masaharu Munetomo (12)
PPT
Realizing Robust and Scalable Evolutionary Algorithms toward Exascale Era
Masaharu Munetomo ?
PDF
Hokkaido University Academic Cloud: Largest Academic Cloud System in Japan
Masaharu Munetomo ?
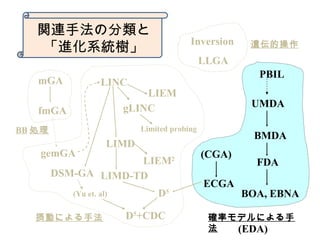
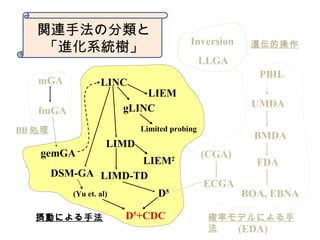
6. 1970年代: Inversion (逆
位)
? 遺伝的アルゴリズムが開発された 1970 年
代当初からリンケージの問題は意識され
、 Holland による最初の本において
も、 Inversion (逆位)が紹介されている
? しかし、密なリンケージをうまく生成で
きない
101010111010101110101.........11
101010111010111010101.........11
7. 80年代~90年代の試み
? messy GA ??? スキーマの直接処理に
よりビルディングブロック候補を探索す
ることで、リンケージの問題解決を試み
る
? fast messy GA ??? messy GA の高速化
、ビルディングブロックフィルタリング
の採用
? linkage learning GA ??? 円環状に符号化
した個体と、2点交叉に類似した遺伝的
操作により、密なリンケージを探索する
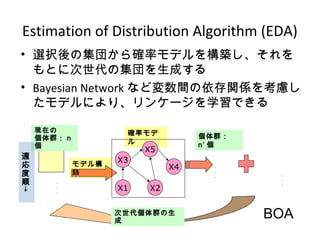
9. Estimation of Distribution Algorithm (EDA)
? 選択後の集団から確率モデルを構築し、それを
もとに次世代の集団を生成する
? Bayesian Network など変数間の依存関係を考慮し
たモデルにより、リンケージを学習できる
個体群:
n’ 個
確率モデ
ル
?
?
? ?
?
?
?
?
?
モデル構
築
現在の
個体群: n
個
次世代個体群の生
成
X3
X1
X5
X2
X4
適
応
度
順
→
BOA
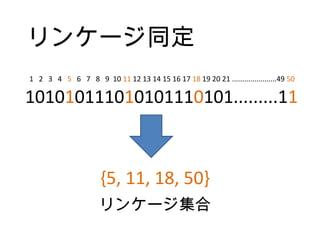
11. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 ......................49 50
101010111010101110101.........11
リンケージ同定
{5, 11, 18, 50}
リンケージ集合
12. LINC (Linkage Identification by
Nonlinearity Check)
? リンケージ同定のために、遺伝子座間で
の 非線形性をチェックする手法
? 線形性?線形分離可能(交叉で探索可能)
? 非線形性?ビルディングブロックとしてま
とめて処理される必要?リンケージとして
認識
? 目的関数そのものの非線形性を知ること
はできないので、 perturbation( 摂動 ) によ
る適応度の変化量を検出することで推定
する
13. 線形分離可能問題
?非線形性は BB 内部にのみ存在(重複な
し)
?遺伝子座のペア (i, j) の選択
)()()()( 2211 nn sfsfsfsf +++= ?
)()()()( 2211 nn sfsfsfsf +++= ?
)()()()( 2211 nn sfsfsfsf +++= ?
i j
i j
線形
非線形※
※ 少なくとも1つの個体において非線形性を示す。
(すべての可能な個体で線形であれば、線形分離可能となる)
14. 適応度の変化を検出
Order-1 perturbations
Order-2 perturbation
O(k2k
) 個の個体 s に対して以下をチェックす
る
If
? (i, j) をリンケージとし
)()1()( ???? iii sfsfsf ??=?
)()1()( ???? jjj sfsfsf ??=?
)()11()( ?????? jijiij ssfssfsf ???=?
)()()( sfsfsf jiij ?+?≠?
15. 摂動によるリンケージ同定手法
? LIMD ??? 非線形性条件を拡張した非単
調性条件をもとにリンケージを同定する
? LIEM, LIEM2
??? LINC, LIMD の条件をも
とにしたエピスタシス尺度を用いてリン
ケージ同定する
? gLINC ??? 高次の摂動を行うことによ
りリンケージを同定する LINC の拡張
? Limited Probing ??? 摂動の概念を一般
化
? hLIEM ??? 階層型のリンケージ構造を
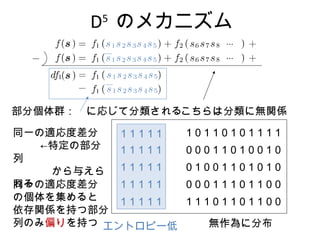
17. エントロピー低
D5
のメカニズム
部分個体群: に応じて分類されるこちらは分類に無関係
1 0 1 1 0 1 0 1 1 1 1
0 0 0 1 1 0 1 0 0 1 0
0 1 0 0 1 1 0 1 0 1 0
1 1 1 0 1 1 0 1 1 0 0
0 0 0 1 1 1 0 1 1 0 0
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
無作為に分布
同一の適応度差分
←特定の部分
列
から与えら
れる同一の適応度差分
の個体を集めると
依存関係を持つ部分
列のみ偏りを持つ
18. 既存手法(まとめ) → 本研究
BOA (Bayesian Optimization Algorithm)
– 適応度評価回数は少なめ O(l1.55
)
– 確率モデル構築のコスト大 O(l3
)
– 適応度への寄与の小さい BB の検出が難しい
摂動によるリンケージ同定 (LINC, LIMD, LIEM....)
– 適応度寄与の大小にかかわらず BB が検出可能
– O(l2
) 回の適応度評価 が必要となる
D5
少ない適応度評価回数 O(l log l)
で
寄与の小さい BBs も
検出できるアルゴリズム
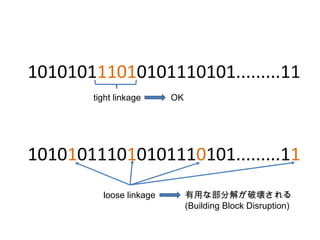
20. Context Dependent Crossover (CDC)
? リンケージ集合の重複構造をグラフで表現
– ノード : リンケージ集合
– 枝 : それらの重複関係
? 交叉ペアとなる個体の値 (Context) に応じてグラフを修
正する
? グラフを最小カットにより2つに分けてそれぞれに属す
るリンケージ集合により交叉を適用 mincut
L1
L2
L3
L4
21 3 54 6 87 9
L1
L3
L4
L2
0 11 1 1 1 0 1 1
22. まとめ
? リンケージ同定の目的 ??? 符号化に依
存せず、問題構造を分析しながら最適化
を行う
? 摂動によるリンケージ同定 ??? 簡単な
アルゴリズムでリンケージを同定できる
が、 O(l2
) の計算コストが必要
? 現状での到達点: D5
+CDC ??? 少ない
計算コスト O(l log l) でリンケージを同定
、重複を有する複雑なリンケージの構造
に対応して良解を生成できる
24. Linkage in Evolutionary
Computation @ CEC2007
? An Empirical Evaluation of Linkage Learning Strategies for Multimodel
Optimization, L. R. Emmendorfer and A. T. R. Pozo
? Case-Based Reasoning and Object-Oriented Data Structures Exploit
Biological Analogs to Generate Virtual Evolutionary Linkages, Corie L.
Cobb, Ying Zhang, Alice M. Agogino and Jennifer Mangold
? A Simple Real-Coded Extended Compact Genetic Algorithm, Luca Fossati,
Pier Luca Lanzi, Kumara Sastry, David E. Goldberg and Osvaldo Gomez
? A Network Design Problem by a GA with Linkage Identication and
Recombination for Overlapping Building Blocks, Miwako Tsuji, Masaharu
Munetomo and Kiyoshi Akama
? Linkage Identication by Perturbation and Decision Tree Induction, Chung-
Yao Chuang and Ying-ping Chen
? The Limitations of Distribution Sampling for Linkage Learning, D. J. Cofn
and R. E. Smith




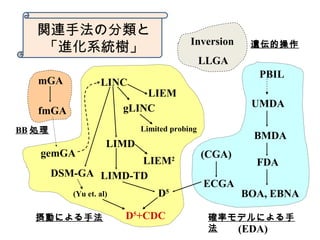








![リンケージ集合の重複への対応
? 現実の問題は複雑な相互作用を有するため、リン
ケージ集合に重複が存在する
? LIMD-TD (tightness detection) ??? LIMD で得ら
れたリンケージ情報から、それぞれの遺伝子の
tightness を計算することで重複を除去
? DSM-GA (Decision Structure Matrix GA) ??? LINC
の条件により得られた行列 [dij] (LINC 条件を満た
す :dij =1) からある尺度を基準にしてリンケージ集
)()()()( 2211 nn sfsfsfsf +++= ?
重複を許す
任意の関数を表現可
能](https://image.slidesharecdn.com/200712-140614193626-phpapp01/85/200712-19-320.jpg)