persamaan lingkaran dan garis singgung
- 1. BAB 4
- 2. Standar Kompetensi: ’ü▒ Menyusun persamaan lingkaran dan garis singgungnya. Kompetensi Dasar: ’ü▒ Menyusun persamaan lingkaran yang memenuhi persyaratan yang ditentukan ’ü▒ Menentukan persamaan garis singgung pada lingkaran dalam berbagai situasi
- 3. PERSAMAAN-PERSAMAAN LINGKARAN Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama terhadap sebuah titik tertentu yang terletak pada bidang datar. Jarak yang sama disebut jari-jari lingkaran dan sebuah titik tertentu disebut pusat lingkaran.
- 4. Untuk tempat kedudukan titik-titik yang membentuk lingkaran, persamaan yang menghubungkan peubah x dan peubah y disebut persamaan lingkaran. Bentuk persamaan lingkaran ditentukan oleh: ŌĆó letak pusat lingkaran M dan ŌĆó panjang jari-jari r.
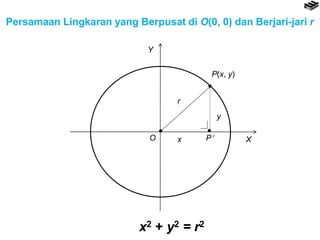
- 5. Persamaan Lingkaran yang Berpusat di O(0, 0) dan Berjari-jari r ’éĘ ’éĘ ’éĘ Y XP’éóO P(x, y) y x r x2 + y2 = r2
- 6. Persamaan Lingkaran yang Berpusat di A(a, b) dan Berjari-jari r AP = (AP’éó)2 + (PP’éó)2 ’āø r = (x ’ĆŁ a)2 + (y ’ĆŁ b)2 ’āø r2 =(x ’ĆŁ a)2 + (y ’ĆŁ b)2 ’āø (x ’ĆŁ a)2 + (y ’ĆŁ b)2 = r2 L ’é║ {(x ’ĆŁ y) l (x ’ĆŁ a)2 + (y ’ĆŁ b)2 = r2} Persamaan lingkaran dengan pusat A(a, b) dan jari-jari r adalah (x ’ĆŁ a)2 + (y ’ĆŁ b)2 = r2
- 7. Bentuk Umum Persamaan Lingkaran Menyatakan Bentuk Umum Persamaan Lingkaran Bentuk umum dari persamaan lingkaran dapat dinyatakan dengan persamaan x2 + y2 + Ax + By + C = 0 (A, B, dan C bilangan-bilangan real) Ax2 + Ay2 + Bx + Cy + D = 0 (A, B, C, dan D bilangan-bilangan bulat, A ’é╣ 0). atau Bentuk umum persamaan lingkaran memiliki ciri-ciri khusus 1. Peubah x dan peubah y berderajat/berpangkat dua dan tidak memuat suku perkalian x dengan y (suku xy). 2. Koefisien x2 sama dengan koefisien y2.
- 8. Menentukan Pusat dan Jari-Jari Lingkaran Pusat dan jari-jari lingkaran L ’é║ x2 + y2 + Ax + By + C = 0 ditentukan dengan rumus: o) pusat A , 2 ’ĆŁ( 2 ’ĆŁ B ) o) jari-jari r = 4 A2 4 B2 + ’ĆŁ C
- 9. Proses menentukan bentuk umum persamaan lingkaran
- 10. POSISI SUATU TITIK TERHADAP LINGKARAN Posisi suatu Titik terhadap Lingkaran L ’é║ x2 + y2 = r2 1. Titik P(a, b) terletak di dalam lingkaran L ’āø a2 + b2 ’Ć╝ r2. 2. Titik P(a, b) terletak pada lingkaran L ’āø a2 + b2 ’Ć╝ r2. 3. Titik P(a, b) terletak di luar lingkaran L ’āø a2 + b2 ’Ć╝ r2. ’éĘ O Y X ’éĘ O Y X ’éĘ O Y X ’éĘ ’éĘ ’éĘ P(a, b) P(a, b) P(a, b) r r r P(a, b) di dalam L P(a, b) pada L P(a, b) di luar L
- 11. Posisi suatu Titik Terhadap Lingkaran L ’é║ (x + a)2 + (y ’ĆŁ b)2 = r2 1. Titik P(h, k) terletak di dalam lingkaran L jika dan hanya jika 2. Titik P(h, k) terletak pada lingkaran L jika dan hanya jika 3. Titik P(h, k) terletak di luar lingkaran jika dan hanya jika (h ’ĆŁ a)2 + (k ’ĆŁ b)2 ’Ć╝ r2 (h ’ĆŁ a)2 + (k ’ĆŁ b)2 = r2 (h ’ĆŁ a)2 + (k ’ĆŁ b)2 ’ĆŠ r2 ’éĘ ’éĘ ’éĘ r r r Y Y Y X X X L L L A(a, b) A(a, b) A(a, b) P(h, k) P(h, k) P(h, k) ’éĘ ’éĘ ’éĘ P(h, k) di dalam L P(h, k) pada L P(h, k) di luar L O O O
- 12. Posisi suatu Titik Terhadap Lingkaran L ’é║ x2 + y2 + Ax + By + C = 0 1. Titik P(h, k) terletak di dalam lingkaran L ’āø K ’Ć╝ 0. 2. Titik P(h, k) terletak pada lingkaran L ’āø K = 0. 3. Titik P(h, k) terletak di luar lingkaran L ’āø K ’ĆŠ 0. Di mana k = h2 + k2 + Ah + Bk + C. Jika titik P(h, k) di luar lingkaran L ’é║ x2 + y2 + Ax + By + C = 0, maka panjang garis singgung yang dibuat melalui titik P(h, k) terhadap lingkaran L ditentukan dengan rumus: dengan S adalah titik singgung dan K adalah kuasa titik P terhadap lingkaran L.p PS = h2 + k2 + Ah + Bk+ C PS = K p atau
- 13. POSISI GARIS TERHADAP LINGKARAN ’éĘ ’éĘ Y Y Y X X X A(x , y ) B(x , y ) ’éĘ ’éĘ ’éĘ’éĘ 2 1 1 2 O O O L L L g g g Memotong lingkaran di dua titik yang berlainan Memotong lingkaran di satu titik atau menyinggung lingkaran Tidak memotong maupun menyinggung lingkaran
- 14. Misalkan garis g dan lingkaran L mempunyai persamaan: g ’é║ ax + by + c = 0, L ’é║ x2 + y2 + Ax + By + C = 0, Posisi garis g terhadap lingkaran L dapat ditentukan melalui langkah-langkah sebagi berikut. Langkah 1 Pada bagian persamaan garis (berbentuk linear), nyatakan x sebagai fungsi y atau y sebagi fungsi x.
- 15. Langkah 2 Subtitusikan x atau y yang diperoleh pada Langkah 1 ke dalam persamaan lingkaran (berbentuk kuadrat). Subtitusi ini menghasilkan persamaan kuadrat dalam peubah x atau y (disebut: persamaaan kudarat gabungan). Kemudian hitunglah nilai diskriminan D dari persamaan kuadrat gabungan itu. Langkah 3 Posisi garis g terhadap lingkaran L ditentukan oleh nilai diskriminan D. 1. D ’ĆŠ 0 ’āø garis g memotong lingkaran L di dua titik yang berlainan. 2. D = 0 ’āø garis g menyinggung lingkaran L. 3. D ’Ć╝ 0 ’āø garis g tidak memotong maupun menyinggung lingkaran L.
- 16. PERSAMAAN GARIS SINGGUNG LINGKARAN Persamaan garis singgung lingkaran yang melalui sebuah titik pada lingkaran Untuk Lingkaran dengan Pusat di O(0,0) dan Jari-Jari r Persamaan garis singgung lingkaran L ’é║ x2 + y2 = r2 yang melalui titik P(x1 , y1 ) pada lingkaran ditentukan dengan rumus sebagai berikut. x1x + y1y = r2
- 17. Untuk Lingkaran dengan Pusat di A(a,b) dan Jari-Jari r Persamaan garis singgung lingkaran L ’é║ (x ’ĆŁ a)2 + (y ’ĆŁ b)2 = r2 yang melalui titik P(x1 , y 1) ditentukan dengan rumus sebagi berikut. (x1 ’ĆŁ a)(x ’ĆŁ a) + (y1 ’ĆŁ b)(y ’ĆŁ b) = r2
- 18. Persamaan Garis Singgung Lingkaran yang Gradiennnya Diketahui Untuk Lingkaran dengan Pusat di O(0,0) dan Jari-Jari r Persamaan garis singgung lingkaran L ’é║ x2 + y2 = r2 dengan gradien m dapat ditentukan dengan rumus sebagai berikut. y = mx ’é▒ r 1+ m2 Untuk Lingkaran dengan Pusat di A(a,b) dan Jari-Jari r Persamaan garis singgung lingkaran L ’é║ (x ’ĆŁ a)2 + (y ’ĆŁ b)2 = r2 dengan gradien m dapat ditentukan dengan rumus sebagi berikut. (y ’ĆŁ b) = m(x ’ĆŁ a) ’é▒ r 1+ m2
- 19. Persamaan Garis Singgung Lingkaran yang melalui Sebuah Titik di Luar Lingkaran
- 20. Cara untuk menentukan persamaan- persamaan garis singgung lingkaran Langkah 1: Persamaan garis yang melalui P(x1 , y 1 ), gradiennya m. Persamaannya adalah y ’ĆŁ y1 = m(x ’ĆŁ x1 ) atau y = mx ’ĆŁ mx 1 + y . Langkah 2: Subtitusikan y = mx ’ĆŁ mx1 + y ke persamaan lingkaran, diperoleh persamaan kuadrat gabungan. Kemudian nilai diskriminan D dari persamaan kuadrat gabungan itu dihitung. Langkah 3: Karena garis lingkaran, nilai diskriminan D = 0. Dari syarat D = 0 diperoleh nilai-nilai m. Subtitusikan niali-nilai m ke persamaan y = mx ’ĆŁ mx1 + y , sehingga diperoleh persamaan-persamaan garis singgung yang diminta.