Karnaugh Map Simplification Rules.pptx
- 1. Prof. Neeraj Bhargava Mrs. Pooja Dixit Department of Computer Science, School of Engineering & System Sciences MDS University Ajmer, Rajasthan
- 2. ’éĪ To minimize the given Boolean function, ’éĪ We draw a K Map according to the number of variables it contains. ’éĪ We fill the K Map with 0ŌĆÖs and 1ŌĆÖs according to its function. ’éĪ Then, we minimize the function in accordance with the following rules. ’éĪ Rule-01: ’éĪ We can either group 0ŌĆÖs with 0ŌĆÖs or 1ŌĆÖs with 1ŌĆÖs but we can not group 0ŌĆÖs and 1ŌĆÖs together. ’éĪ X representing donŌĆÖt care can be grouped with 0ŌĆÖs as well as 1ŌĆÖs. ’éĪ NOTE ’éĪ There is no need of separately grouping XŌĆÖs i.e. they can be ignored if all 0ŌĆÖs and 1ŌĆÖs are already grouped.
- 3. ’éĪ Rule-02: ’éĪ Groups may overlap each other. ’éĪ Rule-03: ’éĪ We can only create a group whose number of cells can be represented in the power of 2. ’éĪ In other words, a group can only contain 2n i.e. 1, 2, 4, 8, 16 and so on number of cells. ’éĪ Example-
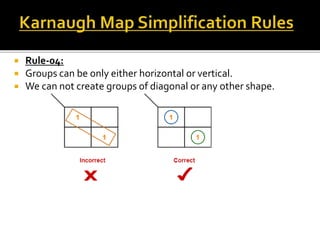
- 4. ’éĪ Rule-04: ’éĪ Groups can be only either horizontal or vertical. ’éĪ We can not create groups of diagonal or any other shape.
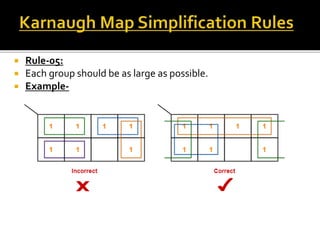
- 5. ’éĪ Rule-05: ’éĪ Each group should be as large as possible. ’éĪ Example-
- 6. ’éĪ Rule-06: ’éĪ Opposite grouping and corner grouping are allowed. ’éĪ The example of opposite grouping is shown illustrated in Rule- 05. ’éĪ The example of corner grouping is shown below. ’éĪ Example- ’éĪ Rule-07: ’éĪ There should be as few groups as possible.