Êýѧ²âÊÔ
0 likes255 views
The document discusses mathematical formulas and proofs. It contains: 1) Formulas for polynomials and series expansions using binomial coefficients. 2) A claim and proof about the series expansion of (1-x)-3 using binomial theorem. 3) Notations showing equivalence and equality of expressions.
1 of 1

Recommended
Ch16 11



Ch16 11schibu20
?
This document contains solutions to 3 functions:
(a) The function f(x)=(2x-3)/(x+8) has x=-8 as its only solution and the domain is all real numbers except -8.
(b) The function f(x)=(x+1)/(2x^2+3x) has solutions of x=0 and x=-3/2 and the domain is all real numbers except -3/2 and 0.
(c) The general function f(x)=(ax+b)/(cx+d) has the solution x=-d/c and the domain is all real numbers except -d/c.Ch14 23



Ch14 23schibu20
?
This document summarizes the solutions to two math word problems:
1) The equations log(xy) = 3, log x = 1, and y are given. Solving these equations yields the solution set {(x = 100; y = 10), (x = -100; y = -10)}.
2) The equations log(x) + log(y) = 2, x + y = 25, and xy = 102 are given. Solving these equations yields the solution set {(x = 5; y = 20), (x = 20; y = 5)}.Derivadas



Derivadasromgarcia
?
This document provides a table summarizing common derivatives and integrals. It lists functions, their derivatives, and integrals in three columns. The derivatives are the powers of x to the exponent minus one, e to the x, 1/x, and a to the x times the natural log of a. The integrals are the powers of x to the exponent plus one over the exponent plus one, e to the x, the natural log of the absolute value of x, and a to the x over the natural log of a plus a constant.Pde unit 1



Pde unit 1Rajini10
?
The document contains solutions to optimization problems using techniques like Lagrange multipliers. The summaries are:
1) Solutions to differential equations involving sin, cos, and exponential terms.
2) Solutions to differential equations involving sin and polynomial terms.
3) Solutions to a differential equation involving polynomials and exponential terms.Fun??es trigonom¨¦tricas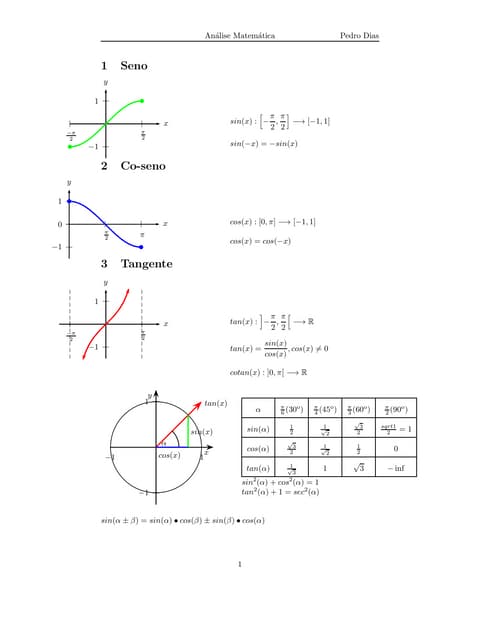



Fun??es trigonom¨¦tricasPedro Dias
?
This document provides definitions and properties for trigonometric functions including sine, cosine, and tangent. It defines the domains and ranges of sine, cosine, and tangent. Examples of trigonometric ratios are given for common angles like 30, 45, 60, and 90 degrees. Trigonometric identities are also listed, such as the sine and cosine of sums and differences of angles.Resumen de Integrales (C¨¢lculo Diferencial e Integral UNAB)



Resumen de Integrales (C¨¢lculo Diferencial e Integral UNAB)Mauricio Vargas ÅÁÏÄ
?
1. This document provides a summary of basic integrals and trigonometric identities relevant for calculus. It lists 20 basic integrals involving functions like x, 1/x, e^x, sin(x), and cotan(x).
2. It also covers integral substitution, integration by parts, and trigonometric identities like sin^2(x) + cos^2(x) = 1.
3. Additional trigonometric identities are presented for functions like sin(x ¡À y), cos(x ¡À y), and tan(x ¡À y) in terms of sums and differences of trigonometric functions.Math Studies Calculus Application



Math Studies Calculus ApplicationChadwick International School
?
The document provides an example problem involving calculus applications to find the local extrema and absolute maximum and minimum of a function f(x) = x^3 - 45x^2 + 600x + 20 on the interval [0,30]. It shows the steps to take the derivative of the function, set it equal to 0 to find critical points, and use the derivative test to determine if the critical points are maxima or minima. The document then evaluates the function at the endpoints of 0 and 30 to determine the absolute maximum and minimum values on the given interval.Ch17 25



Ch17 25schibu20
?
This document discusses calculating the limit of the composition of two functions f and g as x approaches a value. For part (a), as x approaches 0 from the positive side, g(x) approaches 2 from the positive side and f(x) approaches negative infinity as x approaches 2 from the positive side. For part (b), as x approaches 5 from the negative side, g(x) approaches positive infinity and as x approaches positive infinity, f(x) approaches 2.Prof?. Marcelo Santos Chaves - C¨¢lculo I (Limites e Continuidades) - Exerc¨ªci...



Prof?. Marcelo Santos Chaves - C¨¢lculo I (Limites e Continuidades) - Exerc¨ªci...MarcelloSantosChaves
?
1. The document discusses limits and continuities. It provides solutions to calculating the limits of 6 different functions as x approaches certain values.
2. The solutions involve algebraic manipulations such as factoring, simplifying, and applying limit properties. Various limit results are obtained such as 1, -6, 0.
3. The techniques demonstrated include making substitutions to simplify indeterminate forms, factoring, and taking limits of rational functions as the variables approach certain values.5.4 notes



5.4 notesnglaze10
?
This document discusses how to find the x-intercept and y-intercept of a linear equation by setting one variable equal to 0 and solving for the other. It provides examples of finding intercepts from equations, graphing lines using intercepts, and identifying intercepts from a graph.Regras diferenciacao



Regras diferenciacaoUniengenheiros2011
?
1. The document lists rules for differentiation of trigonometric, inverse trigonometric, hyperbolic, inverse hyperbolic, exponential, logarithmic, and other functions.
2. There are 36 rules in total that show how to take the derivative of various functions including sine, cosine, tangent, inverse tangent, hyperbolic sine, hyperbolic tangent, exponentials, logarithms, and more.
3. The rules are presented with the function written on the left side of the equal sign and its derivative written on the right side.Prof? Marcelo Santos Chaves C¨¢lculo I (limites trigonom¨¦tricos)



Prof? Marcelo Santos Chaves C¨¢lculo I (limites trigonom¨¦tricos)MarcelloSantosChaves
?
The document provides solutions to 12 limit problems involving trigonometric functions. Each problem is solved in 3 steps or less. The solutions show that:
1) Many of the limits evaluate to simple numeric values like 1, 0, or constants like a.
2) Trigonometric limits are often solved by factorizing the expressions and applying standard trigonometric limits like lim(sinx/x) = 1 as x approaches 0.
3) More complex problems are broken down into composite limits and simplified through algebraic manipulation and properties of limits.Ejercicio1



Ejercicio1Miguel Silva
?
The document discusses two calculations of the volume of a solid:
1) The volume of a disc bounded by the parabola x + y = 3 and the x-axis is 9¦Ð.
2) The volume of the shell bounded by the same parabola and the planes y = 0 and y = 3 is also 9¦Ð.Mate ejercicios de factorizaci¨®n por binomio - 2?



Mate ejercicios de factorizaci¨®n por binomio - 2?brisagaela29
?
The document contains a series of math problems asking to factorize various expressions. The expressions include variables, numbers, and operations like addition, subtraction, multiplication and exponents. They range in complexity from single term expressions to multi-term expressions involving multiple variables. The goal of the problems is to practice factorizing algebraic expressions.Emat 213 midterm 2 winter 2006



Emat 213 midterm 2 winter 2006akabaka12
?
The document contains a midterm exam for an ODE class with 6 problems worth 10 points each. Problem 1 asks to find the general solution of a 7th order linear ODE using the method of undetermined coefficients. Problem 2 asks to solve a 2nd order linear ODE using either variation of parameters or undetermined coefficients. Problem 3 asks to solve a nonlinear 2nd order ODE using a substitution. Problem 4 asks to find the equation of motion for a mass attached to a spring with an external force applied. Problem 5 asks to solve an eigenvalue problem for a CE equation. Problem 6 asks to use variation of parameters to solve a 2nd order nonhomogeneous ODE.·¡²Ô±ð°ù²µ¨ª²¹



·¡²Ô±ð°ù²µ¨ª²¹Saroff Yataco Irraz¨¢bal
?
This mathematical formula defines the change in temperature (¦¤T) of an object over time as equal to the net rate of heat transfer into the object divided by its specific heat capacity. The net rate of heat transfer is calculated as the sum of the rates of heat transfer by conduction, convection and radiation, minus the sum of the rates of heat transfer out of the object by the same three mechanisms of heat transfer.Mat 128 11 3



Mat 128 11 3zwaneroger8912
?
The document discusses graphing quadratic functions of the form f(x) = ax^2 + bx + c. The key points are:
1) The graph of any quadratic function is a parabola.
2) To graph f(x) = a(x - h)^2 + k, find the vertex (h, k), x-intercepts by setting f(x) = 0, y-intercept, and plot points to form the parabola shape.
3) The vertex of f(x) = ax^2 + bx + c is (-b/2a, f(-b/2a)), which is the minimum if a > 0 and maximum if a1st 2practice



1st 2practicecanalculus
?
1) Find the limit of several functions as x approaches various values.
2) Complete a calculus test covering chapter 1 on limits and continuity.
3) The test contains 12 problems evaluating limits of functions both analytically and graphically.Ejerciciosderivadasresueltos



Ejerciciosderivadasresueltosbellidomates
?
This document provides solutions to calculating the derivative functions of various given functions. It includes:
1) Finding the derivative functions of polynomials, rational functions, exponential functions, logarithmic functions, trigonometric functions, and composite functions.
2) The solutions provide the step-by-step work and final derivative function for each problem.
3) There are over 25 problems covered across multiple pages with the aim of teaching calculation of derivative functions.2? mat em¨¢tica



2? mat em¨¢ticanewtonbonfim
?
This document contains a mathematics chapter about matrices, determinants, and linear systems. It includes examples of matrix operations and solving systems of linear equations. It also contains practice problems related to these topics with solutions.Formulas de taylor



Formulas de taylorERICK CONDE
?
The document discusses Taylor series expansions (desarrollos limitados) and provides 15 examples of applying the Taylor formula to common functions like exponential, logarithmic, trigonometric and hyperbolic functions. Specifically, it gives the Taylor series expansion of each function centered around 0 and in terms of powers of x, along with the little-oh notation describing the remainder term.¼¯ºÏÖª¥×¥í¥°¥é¥ß¥ó¥°¥¼¥ßµÚ£±»Ø



¼¯ºÏÖª¥×¥í¥°¥é¥ß¥ó¥°¥¼¥ßµÚ£±»ØShunta Saito
?
This document discusses various methods for calculating similarity scores between data points, including collaborative filtering, cosine similarity, Euclidean distance, Jaccard similarity, and Tanimoto similarity. It also mentions using word segmentation tools like Mecab for text data preprocessing in Japanese.Fundamental theorem of algebra



Fundamental theorem of algebraRam¨®n Zurita
?
The document discusses several theorems related to polynomials:
1) The Fundamental Theorem of Algebra states that any polynomial of degree greater than 1 with complex coefficients has at least one complex zero.
2) A polynomial of degree n has at most n zeros.
3) A polynomial of degree n greater than 1 with complex coefficients has exactly n complex zeros, if multiplicities are counted.Antiderivatives



AntiderivativesSilvius
?
The indefinite integral of a function f(x) represents the collection of that function's antiderivatives. The general form of an antiderivative is F(x) + C, where F(x) is any function whose derivative is f(x) and C is an arbitrary constant. Some key properties are that the antiderivative of cf(x) is c times the antiderivative of f(x) and the antiderivative of f(x) ¡À g(x) is the antiderivative of f(x) plus/minus the antiderivative of g(x). Tables are also provided listing the antiderivatives of common functions.2 senarai rumus add maths k1 trial spm sbp 2010



2 senarai rumus add maths k1 trial spm sbp 2010zabidah awang
?
The document provides 14 formulae across 4 topics:
1) Algebra - includes formulae for roots of quadratic equations, logarithms, sequences, etc.
2) Calculus - includes formulae for derivatives, integrals, areas under curves, volumes of revolution.
3) Statistics - includes formulae for means, standard deviation, probability, binomial distribution.
4) Geometry - includes formulae for distances, midpoints, areas of triangles, circles, trigonometry ratios.2 senarai rumus add maths k2 trial spm sbp 2010



2 senarai rumus add maths k2 trial spm sbp 2010zabidah awang
?
The document provides 14 formulae across 4 topics:
1) Algebra - includes formulae for roots of quadratic equations, logarithms, sequences, etc.
2) Calculus - includes formulae for derivatives, integrals, areas under curves, volumes of revolution.
3) Statistics - includes formulae for means, standard deviation, probability, binomial distribution.
4) Geometry - includes formulae for distances, midpoints, areas of triangles, circles, trigonometry ratios.Derivatives Table



Derivatives TableSilvius
?
This document provides tables of derivatives for common functions. It lists the derivatives of basic functions like constants, polynomials, logarithms and exponentials. It then gives derivatives of trigonometric functions like sine, cosine, tangent and cotangent. Finally, it provides derivatives of inverse trigonometric functions like arcsine, arccosine, arctangent and arccotangent.Tabela completa de derivadas e integrais



Tabela completa de derivadas e integraisDiego Rodrigues Vaz
?
Tabela para as mat¨¦rias de C¨¢lculo, derivadas, v¨¢rias fun??es ¨²teis e regras de integra??o e deriva??o.last lecture in infinite series



last lecture in infinite seriesAlaa Mohammed
?
(i) The infinite series ¡Æ(2x)n/n from n=1 to infinity is convergent for -1/2 ¡Ü x ¡Ü 1/2 and has an infinite sum of 2x.
(ii) The infinite series ¡Æ((x-1)n)/2n from n=1 to infinity is convergent for -1 < x < 3 and has an infinite sum of x-1.
(iii) The infinite series ¡Æ(n!xn-1) from n=1 to infinity has an interval of convergence of the entire real number line R.Fourier series



Fourier seriesNaveen Sihag
?
The document discusses Fourier series and their properties. Key points include:
1. A Fourier series expresses a periodic function as an infinite sum of sines and cosines. The coefficients are related to the function by definite integrals.
2. Fourier series form a complete set, meaning any periodic function can be represented by a Fourier series. This is shown by comparing Fourier series to Laurent series.
3. Orthogonality relations allow the coefficients of a Fourier series to be determined from the given function.
4. As an example, the sawtooth wave is expressed as a Fourier series that converges to the function as more terms are included.More Related Content
What's hot (20)
Prof?. Marcelo Santos Chaves - C¨¢lculo I (Limites e Continuidades) - Exerc¨ªci...



Prof?. Marcelo Santos Chaves - C¨¢lculo I (Limites e Continuidades) - Exerc¨ªci...MarcelloSantosChaves
?
1. The document discusses limits and continuities. It provides solutions to calculating the limits of 6 different functions as x approaches certain values.
2. The solutions involve algebraic manipulations such as factoring, simplifying, and applying limit properties. Various limit results are obtained such as 1, -6, 0.
3. The techniques demonstrated include making substitutions to simplify indeterminate forms, factoring, and taking limits of rational functions as the variables approach certain values.5.4 notes



5.4 notesnglaze10
?
This document discusses how to find the x-intercept and y-intercept of a linear equation by setting one variable equal to 0 and solving for the other. It provides examples of finding intercepts from equations, graphing lines using intercepts, and identifying intercepts from a graph.Regras diferenciacao



Regras diferenciacaoUniengenheiros2011
?
1. The document lists rules for differentiation of trigonometric, inverse trigonometric, hyperbolic, inverse hyperbolic, exponential, logarithmic, and other functions.
2. There are 36 rules in total that show how to take the derivative of various functions including sine, cosine, tangent, inverse tangent, hyperbolic sine, hyperbolic tangent, exponentials, logarithms, and more.
3. The rules are presented with the function written on the left side of the equal sign and its derivative written on the right side.Prof? Marcelo Santos Chaves C¨¢lculo I (limites trigonom¨¦tricos)



Prof? Marcelo Santos Chaves C¨¢lculo I (limites trigonom¨¦tricos)MarcelloSantosChaves
?
The document provides solutions to 12 limit problems involving trigonometric functions. Each problem is solved in 3 steps or less. The solutions show that:
1) Many of the limits evaluate to simple numeric values like 1, 0, or constants like a.
2) Trigonometric limits are often solved by factorizing the expressions and applying standard trigonometric limits like lim(sinx/x) = 1 as x approaches 0.
3) More complex problems are broken down into composite limits and simplified through algebraic manipulation and properties of limits.Ejercicio1



Ejercicio1Miguel Silva
?
The document discusses two calculations of the volume of a solid:
1) The volume of a disc bounded by the parabola x + y = 3 and the x-axis is 9¦Ð.
2) The volume of the shell bounded by the same parabola and the planes y = 0 and y = 3 is also 9¦Ð.Mate ejercicios de factorizaci¨®n por binomio - 2?



Mate ejercicios de factorizaci¨®n por binomio - 2?brisagaela29
?
The document contains a series of math problems asking to factorize various expressions. The expressions include variables, numbers, and operations like addition, subtraction, multiplication and exponents. They range in complexity from single term expressions to multi-term expressions involving multiple variables. The goal of the problems is to practice factorizing algebraic expressions.Emat 213 midterm 2 winter 2006



Emat 213 midterm 2 winter 2006akabaka12
?
The document contains a midterm exam for an ODE class with 6 problems worth 10 points each. Problem 1 asks to find the general solution of a 7th order linear ODE using the method of undetermined coefficients. Problem 2 asks to solve a 2nd order linear ODE using either variation of parameters or undetermined coefficients. Problem 3 asks to solve a nonlinear 2nd order ODE using a substitution. Problem 4 asks to find the equation of motion for a mass attached to a spring with an external force applied. Problem 5 asks to solve an eigenvalue problem for a CE equation. Problem 6 asks to use variation of parameters to solve a 2nd order nonhomogeneous ODE.·¡²Ô±ð°ù²µ¨ª²¹



·¡²Ô±ð°ù²µ¨ª²¹Saroff Yataco Irraz¨¢bal
?
This mathematical formula defines the change in temperature (¦¤T) of an object over time as equal to the net rate of heat transfer into the object divided by its specific heat capacity. The net rate of heat transfer is calculated as the sum of the rates of heat transfer by conduction, convection and radiation, minus the sum of the rates of heat transfer out of the object by the same three mechanisms of heat transfer.Mat 128 11 3



Mat 128 11 3zwaneroger8912
?
The document discusses graphing quadratic functions of the form f(x) = ax^2 + bx + c. The key points are:
1) The graph of any quadratic function is a parabola.
2) To graph f(x) = a(x - h)^2 + k, find the vertex (h, k), x-intercepts by setting f(x) = 0, y-intercept, and plot points to form the parabola shape.
3) The vertex of f(x) = ax^2 + bx + c is (-b/2a, f(-b/2a)), which is the minimum if a > 0 and maximum if a1st 2practice



1st 2practicecanalculus
?
1) Find the limit of several functions as x approaches various values.
2) Complete a calculus test covering chapter 1 on limits and continuity.
3) The test contains 12 problems evaluating limits of functions both analytically and graphically.Ejerciciosderivadasresueltos



Ejerciciosderivadasresueltosbellidomates
?
This document provides solutions to calculating the derivative functions of various given functions. It includes:
1) Finding the derivative functions of polynomials, rational functions, exponential functions, logarithmic functions, trigonometric functions, and composite functions.
2) The solutions provide the step-by-step work and final derivative function for each problem.
3) There are over 25 problems covered across multiple pages with the aim of teaching calculation of derivative functions.2? mat em¨¢tica



2? mat em¨¢ticanewtonbonfim
?
This document contains a mathematics chapter about matrices, determinants, and linear systems. It includes examples of matrix operations and solving systems of linear equations. It also contains practice problems related to these topics with solutions.Formulas de taylor



Formulas de taylorERICK CONDE
?
The document discusses Taylor series expansions (desarrollos limitados) and provides 15 examples of applying the Taylor formula to common functions like exponential, logarithmic, trigonometric and hyperbolic functions. Specifically, it gives the Taylor series expansion of each function centered around 0 and in terms of powers of x, along with the little-oh notation describing the remainder term.¼¯ºÏÖª¥×¥í¥°¥é¥ß¥ó¥°¥¼¥ßµÚ£±»Ø



¼¯ºÏÖª¥×¥í¥°¥é¥ß¥ó¥°¥¼¥ßµÚ£±»ØShunta Saito
?
This document discusses various methods for calculating similarity scores between data points, including collaborative filtering, cosine similarity, Euclidean distance, Jaccard similarity, and Tanimoto similarity. It also mentions using word segmentation tools like Mecab for text data preprocessing in Japanese.Fundamental theorem of algebra



Fundamental theorem of algebraRam¨®n Zurita
?
The document discusses several theorems related to polynomials:
1) The Fundamental Theorem of Algebra states that any polynomial of degree greater than 1 with complex coefficients has at least one complex zero.
2) A polynomial of degree n has at most n zeros.
3) A polynomial of degree n greater than 1 with complex coefficients has exactly n complex zeros, if multiplicities are counted.Antiderivatives



AntiderivativesSilvius
?
The indefinite integral of a function f(x) represents the collection of that function's antiderivatives. The general form of an antiderivative is F(x) + C, where F(x) is any function whose derivative is f(x) and C is an arbitrary constant. Some key properties are that the antiderivative of cf(x) is c times the antiderivative of f(x) and the antiderivative of f(x) ¡À g(x) is the antiderivative of f(x) plus/minus the antiderivative of g(x). Tables are also provided listing the antiderivatives of common functions.2 senarai rumus add maths k1 trial spm sbp 2010



2 senarai rumus add maths k1 trial spm sbp 2010zabidah awang
?
The document provides 14 formulae across 4 topics:
1) Algebra - includes formulae for roots of quadratic equations, logarithms, sequences, etc.
2) Calculus - includes formulae for derivatives, integrals, areas under curves, volumes of revolution.
3) Statistics - includes formulae for means, standard deviation, probability, binomial distribution.
4) Geometry - includes formulae for distances, midpoints, areas of triangles, circles, trigonometry ratios.2 senarai rumus add maths k2 trial spm sbp 2010



2 senarai rumus add maths k2 trial spm sbp 2010zabidah awang
?
The document provides 14 formulae across 4 topics:
1) Algebra - includes formulae for roots of quadratic equations, logarithms, sequences, etc.
2) Calculus - includes formulae for derivatives, integrals, areas under curves, volumes of revolution.
3) Statistics - includes formulae for means, standard deviation, probability, binomial distribution.
4) Geometry - includes formulae for distances, midpoints, areas of triangles, circles, trigonometry ratios.Derivatives Table



Derivatives TableSilvius
?
This document provides tables of derivatives for common functions. It lists the derivatives of basic functions like constants, polynomials, logarithms and exponentials. It then gives derivatives of trigonometric functions like sine, cosine, tangent and cotangent. Finally, it provides derivatives of inverse trigonometric functions like arcsine, arccosine, arctangent and arccotangent.Tabela completa de derivadas e integrais



Tabela completa de derivadas e integraisDiego Rodrigues Vaz
?
Tabela para as mat¨¦rias de C¨¢lculo, derivadas, v¨¢rias fun??es ¨²teis e regras de integra??o e deriva??o.Prof?. Marcelo Santos Chaves - C¨¢lculo I (Limites e Continuidades) - Exerc¨ªci...



Prof?. Marcelo Santos Chaves - C¨¢lculo I (Limites e Continuidades) - Exerc¨ªci...MarcelloSantosChaves
?
Similar to Êýѧ²âÊÔ (20)
last lecture in infinite series



last lecture in infinite seriesAlaa Mohammed
?
(i) The infinite series ¡Æ(2x)n/n from n=1 to infinity is convergent for -1/2 ¡Ü x ¡Ü 1/2 and has an infinite sum of 2x.
(ii) The infinite series ¡Æ((x-1)n)/2n from n=1 to infinity is convergent for -1 < x < 3 and has an infinite sum of x-1.
(iii) The infinite series ¡Æ(n!xn-1) from n=1 to infinity has an interval of convergence of the entire real number line R.Fourier series



Fourier seriesNaveen Sihag
?
The document discusses Fourier series and their properties. Key points include:
1. A Fourier series expresses a periodic function as an infinite sum of sines and cosines. The coefficients are related to the function by definite integrals.
2. Fourier series form a complete set, meaning any periodic function can be represented by a Fourier series. This is shown by comparing Fourier series to Laurent series.
3. Orthogonality relations allow the coefficients of a Fourier series to be determined from the given function.
4. As an example, the sawtooth wave is expressed as a Fourier series that converges to the function as more terms are included.Fourier series



Fourier seriesNaveen Sihag
?
Fourier series can be used to represent periodic and discontinuous functions. The document discusses:
1. The Fourier series expansion of a sawtooth wave, showing how additional terms improve the accuracy of the representation.
2. How Fourier series are well-suited to represent periodic functions over intervals like [0,2¦Ð] since the basis functions are also periodic.
3. An example of using Fourier series to analyze a square wave, finding the coefficients for its expansion in terms of sines and cosines.Assignment6



Assignment6asghar123456
?
This document contains instructions for 5 assignment questions involving numerical integration and solving differential equations. Question 1 involves using the quad function to evaluate several integrals. Question 2 involves using quad to evaluate Fresnel integrals and plot the results. Question 3 involves using Monte Carlo methods to estimate volumes and double integrals. Question 4 involves using Euler's method to solve an initial value problem and analyze errors. Question 5 involves using lsode to solve a system of differential equations modeling atmospheric circulation and experimenting with initial conditions.Tugas akhir matematika kelompok 1



Tugas akhir matematika kelompok 1Debora Elluisa Manurung
?
This document contains 3 problems:
1) Showing that a sequence is increasing and less than 3.
2) Calculating the average value of a function over an interval.
3) Finding the solution to a partial differential equation of the form 2xyy' ¨C y^2 + x^2 = 0. The solution is found to be y = ¡Ìcx - x^2.Ch33 11



Ch33 11schibu20
?
This document summarizes the solution to an exercise with three parts:
1) Part (a) finds the probability density function f(x) of a random variable X based on its integral from -infinity to infinity being 1. It determines that f(x) = 2 and a = 2.
2) Part (b) calculates the expected value E(x) of X by integrating x*f(x) from 0 to 1. It determines the expected value is 1/3.
3) Part (c) calculates the variance V(X) of X by finding its expected value E(X2) and subtracting the square of its expected value. It determines the variance is 1/Maths assignment



Maths assignmentNtshima
?
1. The document contains an assignment on mathematics involving ordinary and partial differential equations, matrices, vector calculus, and their applications. It includes solving various types of differential equations, finding eigenvectors and eigenvalues of matrices, evaluating line, surface and volume integrals using Green's theorem and Stokes' theorem. The assignment contains 20 problems spanning these topics.
2. The assignment covers key concepts in differential equations, linear algebra, and vector calculus including solving ordinary differential equations, partial differential equations, systems of linear equations, eigenproblems, line integrals, surface integrals, divergence, curl, gradient, Laplacian, and theorems like Green's theorem and Stokes' theorem.
3. Students are required to solve 20 problems involving theseIsm et chapter_3



Ism et chapter_3Drradz Maths
?
- The document discusses linear approximations and Newton's method for finding roots of functions.
- It provides examples of using the linear approximation L(x) = f(x0) + f'(x0)(x - x0) to estimate function values and find roots.
- Newton's method is introduced as xi+1 = xi - f(xi)/f'(xi) to iteratively find better approximations of roots.
- Several examples are worked through step-by-step to demonstrate both linear approximations and Newton's method.Ism et chapter_3



Ism et chapter_3Drradz Maths
?
The document discusses linear approximations of functions. It provides examples of determining:
1) The value of a function f(x) at a point x0 and the derivative f'(x0)
2) The linear approximation L(x) = f(x0) + f'(x0)(x - x0)
3) Using L(x) to estimate the value of f(x) near x0Ism et chapter_3



Ism et chapter_3Drradz Maths
?
The document discusses linear approximations of functions. It provides examples of determining:
1) The value of a function f(x) at a point x0 and the derivative f'(x0)
2) The linear approximation L(x) = f(x0) + f'(x0)(x - x0)
3) Using L(x) to estimate the value of f(x) near x0A family of implicit higher order methods for the numerical integration of se...



A family of implicit higher order methods for the numerical integration of se...Alexander Decker
?
This document presents a family of implicit higher order methods for numerically integrating second order differential equations. The methods are constructed to directly integrate second order ODEs without reformulating them as systems of first order equations. Implicit methods with step numbers from 2 to 6 are developed. Their local truncation errors are analyzed and properties like consistency, symmetry and zero-stability are examined. Numerical examples solved in MATLAB demonstrate that the methods are efficient and accurate compared to existing techniques. The methods are preferable due to their simplicity in derivation, computation and efficiency.Lesson 8: Derivatives of Logarithmic and Exponential Functions (worksheet sol...



Lesson 8: Derivatives of Logarithmic and Exponential Functions (worksheet sol...Matthew Leingang
?
This document provides solutions to derivatives of exponential, logarithmic, and other functions. It includes:
1) The derivatives of functions such as y=e^2x, y=6^x, y=ln(x^3 + 9), and y=log_3(e^x).
2) Using logarithmic differentiation to find the derivatives of functions like y=x^x^2-1 and y=(x-1)(x-2)(x-3).
3) Taking the derivative of functions involving logarithms, exponents, and square roots such as y=sin^2(x)+2sin(x) and y=x(x-1)^3/Math report



Math reportlast4ever
?
1. Find the line tangent to the curve of intersection between the surfaces F(x,y,z)=x^2+y^2+z^2=1 and g(x,y,z)=x+y+z+5 at the point P=(1,2,2).
2. Find the values of constants a and b that will make the expression zxy-zx-zy identically zero, given z=U(x,y)e(ax+by) where Uxy=0.
3. Find the points on the sphere x^2+y^2+z^2=9 whose distance from the point (4,-8,8) areSheet1 simplified



Sheet1 simplifiedmarwan a
?
The document describes a damped mass-spring system and provides the equation of motion for analyzing the free vibration of the system. It then gives the general solution to the differential equation that describes the response x(t) in terms of the system's natural frequency, damping ratio, initial displacement, and initial velocity. The student is asked to:
1. Create a Matlab function to calculate the response x(t) for given parameter values.
2. Run sample code that plots the response for different damping ratios.
3. Calculate and submit the response at two specific cases.Physical Chemistry Assignment Help



Physical Chemistry Assignment HelpEdu Assignment Help
?
I am Frank P. I am a Physical Chemistry Assignment Expert at eduassignmenthelp.com. I hold a Ph.D. in Physical Chemistry, from Malacca, Malaysia. I have been helping students with their homework for the past 6 years. I solve assignments related to Physical Chemistry.
Visit eduassignmenthelp.com or email info@eduassignmenthelp.com.
You can also call on +1 678 648 4277 for any assistance with Physical Chemistry Assignments.Calculus First Test 2011/10/20



Calculus First Test 2011/10/20Kuan-Lun Wang
?
This document contains the work of a student on a calculus test. It includes:
1) Solving limits, finding derivatives, and applying L'Hopital's rule.
2) Using induction to prove an identity.
3) Providing epsilon-delta proofs of limits.
4) Finding where a tangent line is parallel to a secant line.
5) Proving statements about limits of functions.
The student provides detailed solutions showing their work for each problem on the test.Lesson 14: Derivatives of Logarithmic and Exponential Functions (slides)



Lesson 14: Derivatives of Logarithmic and Exponential Functions (slides)Matthew Leingang
?
The exponential function is pretty much the only function whose derivative is itself. The derivative of the natural logarithm function is also beautiful as it fills in an important gap. Finally, the technique of logarithmic differentiation allows us to find derivatives without the product rule. Lesson 14: Derivatives of Logarithmic and Exponential Functions (slides)



Lesson 14: Derivatives of Logarithmic and Exponential Functions (slides)Mel Anthony Pepito
?
This document provides an overview of the key points covered in a calculus lecture on derivatives of logarithmic and exponential functions:
1) It discusses the derivatives of exponential functions with any base, as well as the derivatives of logarithmic functions with any base.
2) It covers using the technique of logarithmic differentiation to find derivatives of functions involving products, quotients, and/or exponentials.
3) The document provides examples of finding derivatives of various logarithmic and exponential functions.03 truncation errors



03 truncation errorsmaheej
?
Let's analyze the remainder term R6 using the geometry series method:
|tj+1| = (j+1)¦Ð-2 ¡Ü ¦Ð-2 = k|tj| for all j ¡Ý 6 (where 0 < k = ¦Ð-2 < 1)
Then, |R6| ¡Ü t7(1 + k + k2 + k3 + ...)
= t7/(1-k)
= 7¦Ð-2/(1-¦Ð-2)
So the estimated upper bound of the truncation error |R6| is 7¦Ð-2/(1-¦Ð-2)Binomial theorem for any index



Binomial theorem for any indexindu psthakur
?
The document summarizes the binomial theorem and properties of binomial coefficients. It provides:
1) The binomial theorem expresses the expansion of (a + b)n as a sum of terms involving binomial coefficients for any positive integer n.
2) Important properties of binomial coefficients are discussed, such as their relationship to factorials and the symmetry of coefficients.
3) Examples are given of using the binomial theorem to find coefficients and solve problems involving divisibility and series of binomial coefficients.Recently uploaded (20)
Entity Framework Interview Questions PDF By ScholarHat



Entity Framework Interview Questions PDF By ScholarHatScholarhat
?
Entity Framework Interview Questions PDF By ScholarHatIntellectual Honesty & Research Integrity.pptx



Intellectual Honesty & Research Integrity.pptxNidhiSharma495177
?
Research Publication & Ethics contains a chapter on Intellectual Honesty and Research Integrity.
Different case studies of intellectual dishonesty and integrity were discussed.NUTRITIONAL ASSESSMENT AND EDUCATION - 5TH SEM.pdf



NUTRITIONAL ASSESSMENT AND EDUCATION - 5TH SEM.pdfDolisha Warbi
?
NUTRITIONAL ASSESSMENT AND EDUCATION, Introduction, definition, types - macronutrient and micronutrient, food pyramid, meal planning, nutritional assessment of individual, family and community by using appropriate method, nutrition education, nutritional rehabilitation, nutritional deficiency disorder, law/policies regarding nutrition in India, food hygiene, food fortification, food handling and storage, food preservation, food preparation, food purchase, food consumption, food borne diseases, food poisoningRRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)



RRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)SONU HEETSON
?
RRB ALP CBT 2 RAC Question Paper MCQ PDF Free Download. Railway Assistant Loco Pilot Mechanic Refrigeration and Air Conditioning Important Questions.Blind spots in AI and Formulation Science, IFPAC 2025.pdf



Blind spots in AI and Formulation Science, IFPAC 2025.pdfAjaz Hussain
?
The intersection of AI and pharmaceutical formulation science highlights significant blind spots¡ªsystemic gaps in pharmaceutical development, regulatory oversight, quality assurance, and the ethical use of AI¡ªthat could jeopardize patient safety and undermine public trust. To move forward effectively, we must address these normalized blind spots, which may arise from outdated assumptions, errors, gaps in previous knowledge, and biases in language or regulatory inertia. This is essential to ensure that AI and formulation science are developed as tools for patient-centered and ethical healthcare.Dr. Ansari Khurshid Ahmed- Factors affecting Validity of a Test.pptx



Dr. Ansari Khurshid Ahmed- Factors affecting Validity of a Test.pptxKhurshid Ahmed Ansari
?
Validity is an important characteristic of a test. A test having low validity is of little use. Validity is the accuracy with which a test measures whatever it is supposed to measure. Validity can be low, moderate or high. There are many factors which affect the validity of a test. If these factors are controlled, then the validity of the test can be maintained to a high level. In the power point presentation, factors affecting validity are discussed with the help of concrete examples.BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAH



BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAHcoacharyasetiyaki
?
BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAHHow to Configure Deliver Content by Email in Odoo 18 Sales



How to Configure Deliver Content by Email in Odoo 18 SalesCeline George
?
In this slide, we¡¯ll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.B? TEST KI?M TRA GI?A K? 2 - TI?NG ANH 10,11,12 - CHU?N FORM 2025 - GLOBAL SU...



B? TEST KI?M TRA GI?A K? 2 - TI?NG ANH 10,11,12 - CHU?N FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
?
https://app.box.com/s/ij1ty3vm7el9i4qfrr41o756xycbahmgHannah Borhan and Pietro Gagliardi OECD present 'From classroom to community ...



Hannah Borhan and Pietro Gagliardi OECD present 'From classroom to community ...EduSkills OECD
?
Hannah Borhan, Research Assistant, OECD Education and Skills Directorate and Pietro Gagliardi, Policy Analyst, OECD Public Governance Directorate present at the OECD webinar 'From classroom to community engagement: Promoting active citizenship among young people" on 25 February 2025. You can find the recording of the webinar on the website https://oecdedutoday.com/webinars/
One Click RFQ Cancellation in Odoo 18 - Odoo ºÝºÝߣs



One Click RFQ Cancellation in Odoo 18 - Odoo ºÝºÝߣsCeline George
?
In this slide, we¡¯ll discuss the one click RFQ Cancellation in odoo 18. One-Click RFQ Cancellation in Odoo 18 is a feature that allows users to quickly and easily cancel Request for Quotations (RFQs) with a single click.Inventory Reporting in Odoo 17 - Odoo 17 Inventory App



Inventory Reporting in Odoo 17 - Odoo 17 Inventory AppCeline George
?
This slide will helps us to efficiently create detailed reports of different records defined in its modules, both analytical and quantitative, with Odoo 17 ERP.Unit 1 Computer Hardware for Educational Computing.pptx



Unit 1 Computer Hardware for Educational Computing.pptxRomaSmart1
?
Computers have revolutionized various sectors, including education, by enhancing learning experiences and making information more accessible. This presentation, "Computer Hardware for Educational Computing," introduces the fundamental aspects of computers, including their definition, characteristics, classification, and significance in the educational domain. Understanding these concepts helps educators and students leverage technology for more effective learning.How to Configure Proforma Invoice in Odoo 18 Sales



How to Configure Proforma Invoice in Odoo 18 SalesCeline George
?
In this slide, we¡¯ll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.Helping Autistic Girls Shine Webinar ºÝºÝߣs



Helping Autistic Girls Shine Webinar ºÝºÝߣsPooky Knightsmith
?
For more information about my speaking and training work, visit: https://www.pookyknightsmith.com/speaking/B? TEST KI?M TRA GI?A K? 2 - TI?NG ANH 10,11,12 - CHU?N FORM 2025 - GLOBAL SU...



B? TEST KI?M TRA GI?A K? 2 - TI?NG ANH 10,11,12 - CHU?N FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
?
Êýѧ²âÊÔ
- 1. Mathtype f ( x) = an x n + an ?1 x n ?1 + L , an ¡Ù 0 an ?1 n ?1 = (x + n x + L), exist an = ( x m + bm ?1 x m ?1 + L) ³Ìʽ¾ŽÝ‹Æ÷ claim: ¡Æ hx n 1 3 n¡Ý0 n = (1 ? x ) 13 + 23 +L + n3 =? A=B A= A1 = A2 = L =B B= B1 = B2 = L =A (1 + x ) 2 =1+2x+ x 2 1 3 1 1 1 2 2 2 Pf: (1 ? x ) = (1 ? x ) (1 ? x ) (1 ? x ) = (1+x+x +L ) (1+x+x +L ) (1+x+x +L ) = ¡Æxei ¡Ý 0 e1 x e2 x e3 = ¡Æx ei ¡Ý 0 e1 + e2 + e3 = ¡Æ (# of sols of e1 + e2 + e3 =n) x n n¡Ý 0 On the other hand,we have by newton¡¯s binomial theorem ? ?3 ? ? n + 2? n ? 2? n ) = ( x ? 1) ?3 = ¡Æ ? ? (? x ) n = ¡Æ ? ? x ? ? = ¡Æ n ¡.(1) 1 3 h xn ( 1? x n¡Ý 0 ?n? n¡Ý 0 ? 2 ? ? 1 ? n¡Ý0




