00_ML Íłįžīą_ÍłįŽ≥łÍįúŽÖź
- 1. Machine Learning Íłįžīą (0) Machine Learning ÍłįŽ≥ł ÍįúŽÖź
- 2. Machine LearningžĚīŽěÄ ‚ÄúA computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.‚ÄĚ - ŪĒĄŽ°úÍ∑łŽě® žä§žä§Ž°ú žĖīŽĖ§ Ž¨łž†úŽ•ľ ŪēīÍ≤įŪē† žąė žěąŽŹĄŽ°Ě Ž™®ŽćłžĚĄ ŪēôžäĶžčúŪā§ŽäĒ žēĆÍ≥†Ž¶¨ž¶ėžĚė ŪÜĶžĻ≠ - ŪēīÍ≤įŪēīžēľ ŪēėŽäĒ Ž¨łž†úžôÄ žÉĀŪô©žóź ŽĒįŽĚľ ž†Āž†ąŪēú ÍłįŽ≤ēžĚĄ žĄ†ŪÉĚ - ŪēôžäĶžĚė ÍłįŽ≥ł : ‚Äėž†Āžö© ÔɆ ŪŹČÍįÄ (ŪĒľŽďúŽįĪ)ÔɆ žąėž†ē(žóÖŽćįžĚīŪäł)‚ÄôžĚė ŽįėŽ≥Ķ - žėąžł° (ex. Ž∂ÄŽŹôžāį ÍįÄÍ≤©, Žā†žĒ® ŽďĪ) - Ž∂ĄŽ•ė (ex. žĚīŽĮłžßÄ, Íłįžā¨, žÜĆŽĻĄžěź Segment ŽďĪ) - Linear Regression - Logistic Regression - Classification / Clustering - Neural Network
- 3. Supervised vs. Unsupervised Learning - Í≥ĶŽ∂ÄŪēėŽäĒ Žį©Ž≤ēžĚÄ ŪĀ¨Í≤Ć ŽĎź ÍįÄžßÄžĚīŽč§! : ŽąĄÍĶįÍįÄžĚė ÍįÄžĚīŽďúŽ•ľ ŽįõÍĪįŽāė Žāė Ūėľžěź ž£ĹžĖīŽĚľ ŪēėÍĪįŽāė - Supervised Learning (žßÄŽŹĄŪēôžäĶ) Ôāß ŽāīÍįÄ žąėŪēô Ž¨łž†úŽ•ľ ŽßěÍ≤Ć ŪíÄžóąŽäĒžßÄ ŪčÄŽ†łŽäĒžßÄ ŽčĶžēąžßÄŽ•ľ Ž≥īÍ≥† žĪĄž†źŪēėŽäĒ Í≤É Ôāß Labeled Training SetžĚī ž£ľžĖīžßĄ ŪēôžäĶŽ≤ē. Ôāß žėąŽ•ľ Žď§žĖī, 1000ÍįúžĚė žĚīŽĮłžßÄŽ•ľ ÍįÄžßÄÍ≥† žĚīŽĮłžßÄ Ž∂ĄŽ•ėŪēėŽäĒ žēĆÍ≥†Ž¶¨ž¶ėžĚĄ ŪēôžäĶžčúžľú ŽāėÍįĄŽč§Í≥† ŪēėŽ©ī, 1Ž≤ąžĚÄ Í≥†žĖĎžĚī žĚīŽĮłžßÄŽĚľŽäĒ ž†ēŽčĶžĚī ž£ľžĖīžßÄÍłį ŽēĆŽ¨łžóź Ž™®Žćłžóź ŽĒįŽĚľ Ž∂ĄŽ•ėŪĖąžĚĄ ŽēĆ 1Ž≤ąžĚĄ žěźŽŹôžį® žĚīŽĮłžßÄŽ°ú Ž∂ĄŽ•ėŪē† Í≤Ĺžöį, Ž™®ŽćłžĚĄ žąėž†ēŪēīžēľ ŪēúŽč§ŽäĒ ŪĒľŽďúŽįĪžĚĄ ž§ÄŽč§. * Labeled Data : a group of samples that have been tagged with one or more labels (Wikipedia). ŽćįžĚīŪĄįžóź ŽĆÄŪēú ž†ēŽ≥īÍįÄ ŪĎúžčúŽźėžĖī žěąŽäĒ ŽćįžĚīŪĄį Í∑łŽ£ĻžĚĄ ŽāėŪÉÄŽāłŽč§. žėąŽ•ľ Žď§žĖī, žĚīŽĮłžßÄ Ž∂ĄžĄĚžóźžĄú, AŽäĒ Í≥†žĖĎžĚī žĚīŽĮłžßÄ, BŽäĒ žěźŽŹôžį® žĚīŽĮłžßÄŽĚľŽäĒ Í≤ɞ̥ ŽĮłŽ¶¨ ž†ēŽ¶¨ŪēīŽÜďžĚÄ ŽćįžĚīŪĄį Í∑łŽ£ĻžĚĄ Labeled DataŽĚľÍ≥† ŪēúŽč§. Labeled DataŽäĒ žßÄŽŹĄŪēôžäĶ ÍłįŽ≤ēžóźžĄú Training Setžóź žā¨žö©ŪēúŽč§. * Training Set : ŪēôžäĶžčúŪā® Ž™®ŽćłžĚė ž†ēŪôēŽŹĄŽ•ľ ŪĆźŽč®ŪēėÍłį žúĄŪēīžĄú Ž≥īŪÜĶ Training SetÍ≥ľ Test SetžĚĄ ŽāėŽą†žĄú ŪŹČÍįÄŪēúŽč§. 1000ÍįúžĚė ŽćįžĚīŪĄįÍįÄ žěąžĚĄ ŽēĆ 700ÍįúžĚė ŽćįžĚīŪĄį(Training Set)Ž°ú Ž™®ŽćłžĚĄ ŪēôžäĶžčúŪā® Žč§žĚĆ, ŪēīŽčĻ Ž™®ŽćłžĚĄ Test Setžóź ž†Āžö©Ūēėžó¨ ž†ēŪôēŽŹĄŽ•ľ žł°ž†ēŪēėŽäĒ Í≤ÉžĚīŽč§. Training SetžóźžĄúŽäĒ ž†ēŪôēŽŹĄÍįÄ ŽÜíŽćė Ž™®ŽćłžĚī Test SetžóźžĄúŽäĒ ž†ēŪôēŽŹĄÍįÄ ŽāģžēĄžßĄŽč§Ž©ī Ž™®ŽćłžĚī ŪäĻž†ē Training SetžóźŽßĆ Žßěž∂įžĄú ŪēôžäĶŽźėžóąŽč§Í≥† ŪĆźŽč®ŪēėÍ≥†, žĚīŽ•ľ Training Setžóź Over-fit ŽźėžóąŽč§Í≥† ŪēúŽč§.
- 4. Supervised vs. Unsupervised Learning - Unsupervised Learning (ŽĻĄžßÄŽŹĄŪēôžäĶ) Ôāß žĪĄž†źŪē† ŽčĶžēąžßÄÍįÄ žóÜŽč§! Ôāß Ž™®ŽćłžĚĄ ŽćįžĚīŪĄįžóź ž†Āžö©ŪĖąžĚĄ ŽēĆ Í≤įÍ≥ľÍįíÍ≥ľ ŽĻĄÍĶźŪē† žąė žěąŽäĒ ž†ēŽčĶžĚī žóÜŽč§. Labeled DataÍįÄ ž£ľžĖīžßÄžßÄ žēäŽäĒŽč§. Ôāß ÍĶ¨ÍłÄ ŽČīžä§Ž•ľ žėąŽ°ú Žď§Ž©ī, žąėŽßéžĚÄ Íłįžā¨ÍįÄ ŽćįžĚīŪĄįŽ°ú ž£ľžĖīžßÄžßÄŽßĆ ‚ÄėA Íłįžā¨ŽäĒ (ÍįÄ) žĚīžäąžóź ŽĆÄŪēú Íłįžā¨žĚīÍ≥†, B Íłį žā¨ŽäĒ (Žāė) žĚīžäąžóź ŽĆÄŪēú Íłįžā¨‚ÄôŽĚľŽäĒ ŽćįžĚīŪĄį ŽĚľŽ≤®žĚÄ ž£ľžĖīžßÄžßÄ žēäŽäĒŽč§. ŪēėžßÄŽßĆ ŽĻĄžßÄŽŹĄŪēôžäĶ ÍłįŽ≤ēžĚĄ žā¨žö©ŪēīžĄú ŽćįžĚīŪĄį ÍįĄžĚė žóįÍīÄžĄĪžĚĄ žįĺžēĄŽāī žěźŽŹôžúľŽ°ú ÍįôžĚÄ žĚīžäąŽ•ľ Žč§Ž£®Í≥† žěąŽäĒ žó¨Žü¨ Íłįžā¨Ž•ľ Í∑łŽ£ĻŪēĎŪēīžĄú žā¨žö©žěźžóźÍ≤Ć Ž≥īžó¨ž§ÄŽč§.
- 5. Structured vs. Unstructured Data - Ž∂ĄŽ•ėŽźėžĖī žěąŽäĒ ŽćįžĚīŪĄįžôÄ Í∑łŽ†ážßÄ žēäžĚÄ ŽćįžĚīŪĄį - ÍįÄžě• ŽßéžĚī žā¨žö©ŪēėŽäĒ žėąžĚł žēĄŪĆĆŪäł ÍįÄÍ≤© žėąžł° Ž¨łž†úŽ•ľ žėąŽ°ú žÉĚÍįĀŪēīŽ≥īžěź. žēĄŪĆĆŪäł ÍįÄÍ≤©žóź žėĀŪĖ•žĚĄ ŽĮłžĻ† žąė žěąŽäĒ žöĒžĚłŽď§, Žį© Íįúžąė, ŪŹČžąė, žúĄžĻė, ÍĪīŽ¨ľ ŽÜížĚī, ÍįÄÍĶ¨žąė ŽďĪžĚĄ Íłįž§ÄžúľŽ°ú ÍįĀ žēĄŪĆĆŪäł žĄłŽĆÄžĚė ŽćįžĚīŪĄįŽ•ľ ŪĎúžčúŪē† žąė žěąŽč§ (Structured Data). - ŪēėžßÄŽßĆ ÍłÄžĚĄ ŪÜĶŪēī ͳĞďīžĚīžĚė žč¨Ž¶¨Ž•ľ Ž∂ĄžĄĚŪēėŽäĒ Ž¨łž†úÍįÄ žěąŽč§Í≥† ÍįÄž†ēŪēėŽ©ī, AŽĚľŽäĒ žā¨ŽěĆžĚī žěĎžĄĪŪēú ÍłÄ ž†Ą ž≤īÍįÄ ŽćįžĚīŪĄįÍįÄ Žź† Í≤ɞ̳Žćį, ŪÖćžä§Ūäł ŽćįžĚīŪĄįžĚė Í≤Ĺžöį žúĄžôÄ ÍįôžĚī žĖīŽĖ§ ž†ēŽŹąŽźú ŪėēŪÉúŽ°ú ÍĶ¨žĄĪŪēėÍłį žČĹžßÄ žēäŽč§ (Unstructured Data).
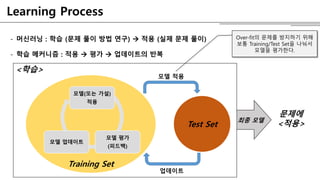
- 6. - Ž®łžč†Žü¨ŽčĚ : ŪēôžäĶ (Ž¨łž†ú ŪíÄžĚī Žį©Ž≤ē žóįÍĶ¨) ÔɆ ž†Āžö© (žč§ž†ú Ž¨łž†ú ŪíÄžĚī) - ŪēôžäĶ Ž©ĒžĽ§Žčąž¶ė : ž†Āžö© ÔɆ ŪŹČÍįÄ ÔɆ žóÖŽćįžĚīŪäłžĚė ŽįėŽ≥Ķ Training Set <ŪēôžäĶ> Learning Process Ž™®Žćł(ŽėźŽäĒ ÍįÄžĄ§) ž†Āžö© Ž™®Žćł ŪŹČÍįÄ (ŪĒľŽďúŽįĪ) Ž™®Žćł žóÖŽćįžĚīŪäł žĶúžĘÖ Ž™®Žćł Ž¨łž†úžóź <ž†Āžö©>Test Set Ž™®Žćł ž†Āžö© žóÖŽćįžĚīŪäł Over-fitžĚė Ž¨łž†úŽ•ľ Žį©žßÄŪēėÍłį žúĄŪēī Ž≥īŪÜĶ Training/Test SetžĚĄ ŽāėŽą†žĄú Ž™®ŽćłžĚĄ ŪŹČÍįÄŪēúŽč§.
- 7. Ž™®Žćł ŪŹČÍįÄ (žÜźžč§ Ūē®žąė, Loss Function) - žĄ§ž†ēŪēú Ž™®ŽćłžĚĄ ž†Āžö©ŪēėÍ≥† ŪēīŽčĻ Ž™®ŽćłžĚī Ūö®Í≥ľž†ĀžĚłžßÄ ŪĆźŽč®ŪēėŽ©īžĄú ŪēôžäĶžĚī žßĄŪĖČŽźėŽäĒŽćį Í≥ľžóį žĖīŽĖ§ Íłįž§Ä žúľŽ°ú ŪĆźŽč®Ūē† Í≤ɞ̳ÍįÄ - žÜźžč§Ūē®žąė(Loss Function) : ŪėĄžě¨žĚė Ž™®ŽćłŽ°ú žėąžł°Ūēú Í≤įÍ≥ľÍįížĚī ŪõąŽ†® ŽćįžĚīŪĄįžĚė ‚Äėž†ēŽčĶ‚ÄôÍ≥ľ žĖľŽßąŽāė žį®žĚī ŽāėŽäĒžßÄ ÍĶ¨ŪēėŽäĒ Ūē®žąė, ÍįížĚī žěϞ̥žąėŽ°Ě žĄĪŽä•žĚī žĘčžĚÄ Ž™®ŽćłžĚīŽĚľŽäĒ Í≤ɞ̥ žĚėŽĮłŪēúŽč§. Ôāß ŪŹČÍ∑† ž†úÍ≥Ī žė§žį® (Mean Squared Error, MSE) Ôāß ÍĶźžį® žóĒŪ䳎°úŪĒľ žė§žį® (Cross Entropy Error, CEE)
- 8. Ž™®Žćł žóÖŽćįžĚīŪäł (Gradient Descent) - žā¨žö©Ūēú Ž™®ŽćłžĚĄ ŪŹČÍįÄŪēú žĚīŪõĄ Í≤įÍ≥ľžóź ŽĒįŽ•ł ŪĒľŽďúŽįĪžĚĄ ž£ľŽäĒ Í≤ÉžĚī ŪēĄžöĒ - ŪĒľŽďúŽįĪ, ž¶Č Ž™®ŽćłžĚĄ žóÖŽćįžĚīŪäł ŪēėŽäĒ Žį©Ž≤ēžĚÄ žó¨Žü¨ ÍįÄžßÄÍįÄ žěąžßÄŽßĆ ŽĆÄŽ∂ÄŽ∂ĄžĚė ÍłįŽ≤ēžĚÄ ÍįÄžě• ÍłįŽ≥łžĚī ŽźėŽäĒ Í≤Ĺžā¨ŪēėÍįēŽ≤ē (Gradient Descent)žóźžĄú ŪĆĆžÉĚŽźú Í≤Ɏ硫°ú žĚīŪēīŪē† žąė žěąŽč§. - ŪēôžäĶžĚė Ž™©ŪĎúŽäĒ žÜźžč§Ūē®žąė ÍįížĚĄ žĶúžÜĆŪôĒŪēėŽäĒ Í≤É! * Ūē®žąė Í∑łŽěėŪĒĄÍįÄ žēĄŽěėŽ°ú žė§Ž™©Ūēú ŪŹ¨Ž¨ľžĄ†žĚľ ŽēĆ, Í∑łŽěėŪĒĄžĚė ÍłįžöłÍłįÍįÄ 0žĚł žßÄž†źžĚī Ūē®žąėžĚė žĶúžÜĆÍįí Ž™®ŽćłžĚī Ž≥Ķžě°ŪēīžßąžąėŽ°Ě žÜźžč§Ūē®žąė Í∑łŽěėŪĒĄ žó≠žčú Ž≥Ķžě°ŪēīžßÄÍłį ŽēĆŽ¨łžóź 2žį® Ūē®žąė Í∑łŽěėŪĒĄž≤ėŽüľ ÍłįžöłÍłįÍįÄ 0žĚł žßÄž†źžĚĄ žČĹÍ≤Ć žįĺžĚĄ žąė žó܎觎äĒ Ž¨łž†úÍįÄ ŽįúžÉĚŪēúŽč§. Í≤Ĺžā¨ŪēėÍįēŽ≤ē(Gradient Descent)žĚė ÍłįŽ≥łž†ĀžĚł žēĄžĚīŽĒĒžĖīŽäĒ žĚīŽ†áŽč§. žöįŽ¶¨ÍįÄ ŪēôžäĶžĚĄ Ūē† ŽēĆ Ž≥Ķžě°Ūēú žÜźžč§Ūē®žąė Í∑łŽěėŪĒĄžĚė ž†Ąž≤īž†ĀžĚł Ž™®žĖĎžĚÄ žēĆ žąė žóÜžßÄŽßĆ ž†ĀžĖīŽŹĄ ŪėĄžě¨ žúĄžĻėžóźžĄúžĚė žąúÍįĄ ÍłįžöłÍłį(Gradient, ŽĮłŽ∂Ą Íįí)ŽäĒ žēĆ žąė žěąÍłį ŽēĆŽ¨łžóź ÍłįžöłÍłį Žį©ŪĖ•žúľŽ°ú ž°įÍłąžĒ© ŽāīŽ†§ÍįĄŽč§Ž©ī(Descent) ÍłįžöłÍłįÍįÄ 0žĚł žßÄž†źžóź Žč§Žč§Ž•ľ žąė žěąžĚĄ Í≤ÉžĚīŽč§.
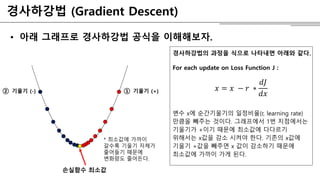
- 9. Í≤Ĺžā¨ŪēėÍįēŽ≤ē (Gradient Descent) ‚ÄĘ žēĄŽěė Í∑łŽěėŪĒĄŽ°ú Í≤Ĺžā¨ŪēėÍįēŽ≤ē Í≥Ķžč̞̥ žĚīŪēīŪēīŽ≥īžěź. Í≤Ĺžā¨ŪēėÍįēŽ≤ēžĚė Í≥ľž†ēžĚĄ žčĚžúľŽ°ú ŽāėŪÉÄŽāīŽ©ī žēĄŽěėžôÄ ÍįôŽč§. For each update on Loss Function J : ūĚĎ• = ūĚĎ• ‚ąí ūĚĎü ‚ąó ūĚĎĎū̟ŠūĚĎĎūĚĎ• Ž≥Äžąė xžóź žąúÍįĄÍłįžöłÍłįžĚė žĚľž†ēŽĻĄžú®(r, learning rate) ŽßĆŪĀľžĚĄ ŽĻľž£ľŽäĒ Í≤ÉžĚīŽč§. Í∑łŽěėŪĒĄžóźžĄú 1Ž≤ą žßÄž†źžóźžĄúŽäĒ ÍłįžöłÍłįÍįÄ +žĚīÍłį ŽēĆŽ¨łžóź žĶúžÜĆÍįížóź Žč§Žč§Ž•īÍłį žúĄŪēīžĄúŽäĒ xÍįížĚĄ ÍįźžÜĆ žčúžľúžēľ ŪēúŽč§. Íłįž°īžĚė xÍįížóź ÍłįžöłÍłį +ÍįížĚĄ ŽĻľž£ľŽ©ī x ÍįížĚī ÍįźžÜĆŪēėÍłį ŽēĆŽ¨łžóź žĶúžÜĆÍįížóź ÍįÄÍĻĆžĚī ÍįÄÍ≤Ć ŽźúŽč§. žÜźžč§Ūē®žąė žĶúžÜĆÍįí ‚Ď† ÍłįžöłÍłį (+)‚Ď° ÍłįžöłÍłį (-) * žĶúžÜĆÍįížóź ÍįÄÍĻĆžĚī ÍįąžąėŽ°Ě ÍłįžöłÍłį žěźž≤īÍįÄ ž§ĄžĖīŽď§Íłį ŽēĆŽ¨łžóź Ž≥ÄŪôĒŽüČŽŹĄ ž§ĄžĖīŽď†Žč§.
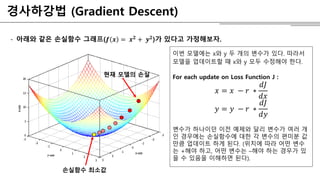
- 10. Í≤Ĺžā¨ŪēėÍįēŽ≤ē (Gradient Descent) - žēĄŽěėžôÄ ÍįôžĚÄ žÜźžč§Ūē®žąė Í∑łŽěėŪĒĄ(ūĚíá ūĚíô = ūĚíô ūĚüź + ūĚíö ūĚüź)ÍįÄ žěąŽč§Í≥† ÍįÄž†ēŪēīŽ≥īžěź. žÜźžč§Ūē®žąė žĶúžÜĆÍįí ŪėĄžě¨ Ž™®ŽćłžĚė žÜźžč§ žĚīŽ≤ą Ž™®ŽćłžóźŽäĒ xžôÄ y ŽĎź ÍįúžĚė Ž≥ÄžąėÍįÄ žěąŽč§. ŽĒįŽĚľžĄú Ž™®ŽćłžĚĄ žóÖŽćįžĚīŪäłŪē† ŽēĆ xžôÄ y Ž™®ŽĎź žąėž†ēŪēīžēľ ŪēúŽč§. For each update on Loss Function J : ūĚĎ• = ūĚĎ• ‚ąí ūĚĎü ‚ąó ūĚĎĎū̟ŠūĚĎĎūĚĎ• ūĚ϶ = ūĚ϶ ‚ąí ūĚĎü ‚ąó ūĚĎĎū̟ŠūĚĎĎūĚ϶ Ž≥ÄžąėÍįÄ ŪēėŽāėžĚīŽćė žĚīž†Ą žėąž†úžôÄ Žč¨Ž¶¨ Ž≥ÄžąėÍįÄ žó¨Žü¨ Íįú žĚł Í≤ĹžöįžóźŽäĒ žÜźžč§Ūē®žąėžóź ŽĆÄŪēú ÍįĀ Ž≥ÄžąėžĚė Ū鳎ĮłŽ∂Ą Íįí ŽßĆŪĀľ žóÖŽćįžĚīŪäł ŪēėÍ≤Ć ŽźúŽč§. (žúĄžĻėžóź ŽĒįŽĚľ žĖīŽĖ§ Ž≥Äžąė ŽäĒ +Ūēīžēľ ŪēėÍ≥†, žĖīŽĖ§ Ž≥ÄžąėŽäĒ ‚ÄďŪēīžēľ ŪēėŽäĒ Í≤ĹžöįÍįÄ žěą žĚĄ žąė žěąžĚƞ̥ žĚīŪēīŪēėŽ©ī ŽźúŽč§).