01 i 02 Matrius i determinants
- 1. Tema 1 i 2: Matrius i determinants 1. Nomenclatura i classificaci├│ 2. Operacions amb matrius 3. C├Ālcul de determinants 4. Menors i adjunts d'una matriu quadrada 5. Propietats dels determinants 6. El rang d'una matriu 7. Matrius inverses
- 2. 1. Nomenclatura i classificaci├│ p8 1,2,3,4,5,6 element ( a11 a12 a13 ... a1n a21 a22 a23 ... a2n ... ... ... ... ... am1 am2 am3 ... amn ) columna fila Ordre: m x n Tipus de matrius: matriu fila, matriu columna, matriu nul┬Ęla, matriu oposada, matriu quadrada d'ordre tal, matriu rectangular, matriu transposada (t A), matrius iguals.
- 3. Tipus de matrius quadrades: matriu triangular superior, matriu triangular inferior, matriu diagonal, matriu escalar, matriu identitat o unitat (I). Nom├®s en les matrius quadrades: -Matrius sim├©triques: A = At , per tant aij = aji -Matrius antisim├©triques: -A = At , per tant -aij = aji A= ( a m n m b v n v c) A= ( a m n ŌłÆm b v ŌłÆn ŌłÆv c)p11 7, 8, 9, 10, 11 Conceptes: diagonal principal, secund├Āria i tra├¦a.
- 4. 2. Operacions amb matrius Suma i resta: A + B = C, essent cij = aij + bij Multiplicaci├│ per un nombre: k ┬Ę A = C, essent cij = k ┬Ę aij Multiplicaci├│ d'una matriu fila per una matriu columna: (a11 a12 ... a1n )┬Ę ( b11 b21 ... bn1 )=a11 ┬Ęb11+a12 ┬Ęb21+...+a1n ┬Ębn1 ( b11 b21 ... bm1 )┬Ę(a11 a12 ... a1n )= ( b11 ┬Ęa11 b11 ┬Ęa12 ... b11 ┬Ęa1n b21 ┬Ęa11 b21 ┬Ęa12 ... b21 ┬Ęa1n ... ... ... ... bm1┬Ęa11 bm1┬Ęa12 ... bm1┬Ęa1n ) ŌĆ£El resultat t├® tantes files com files t├® el primer factor (el primer mana)ŌĆØ
- 5. Multiplicaci├│ de dues matrius: p15 12,13,14,16abcd,17,19,20 Activitats finals: 5,10,12,17,22a (c11 c12 c21 c22 ) -Nom├®s podrem multiplicar dues matrius si el nombre de columnes de la primera coincideix amb el nombre de files de la segona. -La resultant t├® tantes files com la primera i tantes columnes com la segona. -Atenci├│: en general, NO es presenta la propietat commutativa. (5 ŌłÆ3 4 0 1 2)┬Ę ( 4 2 0 5 1 3)= c11=5┬Ę 4+(ŌłÆ3)┬Ę0+4┬Ę1=24 c21=0┬Ę4+1┬Ę0+2┬Ę1=2 c12=5┬Ę 2+(ŌłÆ3)┬Ę5+4┬Ę3=7 c22=0┬Ę2+1┬Ę5+2┬Ę3=11 =(24 7 2 11)
- 6. 3. C├Ālcul de determinants Exemples r├Āpids D'ordre 2 i 3: La regla de Sarrus A= (a11 a12 a21 a22 ) ŌłŻAŌłŻ= ŌłŻa11 a12 a21 a22 ŌłŻ=a11 ┬Ęa22ŌłÆa12 ┬Ęa21 A= ( a11 a12 a13 a21 a22 a23 a31 a32 a33 ) ŌłŻAŌłŻ= ŌłŻ a11 a12 a13 a21 a22 a23 a31 a32 a33 ŌłŻ=a11 ┬Ęa22 ┬Ęa33+a12 ┬Ęa23 ┬Ęa31 +a21 ┬Ęa32 ┬Ęa13ŌłÆa13 ┬Ęa22 ┬Ęa31ŌłÆa12┬Ęa21 ┬Ęa33ŌłÆa23┬Ęa32 ┬Ęa11 p22 1,2,3,4
- 7. A= ( 1 2 1 ŌłÆ3 3 0 ŌłÆ2 4 1) -Menor complementari d'un element: ├®s el determinant de la matriu resultant d'eliminar la fila i la columna a les quals pertany l'element. p23 E2 M 21= ŌłŻ2 1 4 1ŌłŻ=ŌłÆ2 A= ( 1 2 1 ŌłÆ3 3 0 ŌłÆ2 4 1) -Adjunt d'un element: ├®s el determinant de la matriu resultant d'eliminar la fila i la columna a les quals pertany l'element, amb el signe canviat segons si ŌĆ£i + jŌĆØ ├®s parell o senar. Fer alguns exemples m21= (ŌłÆ1)2+1 ┬ĘŌłŻ2 1 4 1ŌłŻ=ŌłÆ1┬Ę(ŌłÆ2)=2 4. Menors i adjunts d'una matriu quadrada
- 8. E4, E5, p26: 6, 9 i 10 Determinant d'una matriu qualsevol: ├ēs igual a la suma dels productes dels elements d'una fila o columna qualsevol pels seus adjunts corresponents. A= ( 1 2 1 ŌłÆ3 3 0 ŌłÆ2 4 1) -Matriu adjunta: ├®s la matriu resultant de fer els adjunts de cada un dels elements. p24 E3 Adj(A)= ( 3 3 ŌłÆ6 2 3 ŌłÆ8 ŌłÆ3 ŌłÆ3 9 )
- 9. 5. Propietats dels determinants Exemple ordre 3 ŌłŻ k ┬Ęa11 k ┬Ęa12 k ┬Ęa13 a21 a22 a23 a31 a32 a33 ŌłŻ=k ┬ĘŌłŻAŌłŻ Exemple ordre 3 1a) |A| = |At | 2a) Si en una matriu quadrada intercanviem dues files, o dues columnes, el determinant canv├»a de signe. Exemple ordre 3 3a) Si multipliquem per un mateix nombre tots els elements d'una mateixa fila, o columna, el seu determinant queda multiplicat per aquest nombre. Atenci├│!: |k┬ĘA| = kn ┬Ę |A| Exemple ordre n=3
- 10. Exemple ordre 3 Exemples ordre 3 4a) Si t├® una fila o columna de 0's, el determinant ├®s 0. 5a) Si a una fila o columna li sumem* una combinaci├│ lineal de les altres, el determinant no varia. *no val multiplicar la fila que variem, pq sin├│ multiplicar├Łem tamb├® el valor del determinant (prop. 3) Exemple ordre 3+ exemple per propietats 6a) Si t├® dues files o dues columnes iguals o proporcionals, el determinant ├®s 0.
- 11. Exemple ordre 3 Exemples ordre 3 7a) Si t├® una fila o columna que ├®s combinaci├│ lineal de les altres, el determinant ├®s 0. 8a) Un determinant es pot descomposar en la suma d'uns altres dos determinants separant una fila o columna en dos sumands. Exemple ordre 3 9a) |A ┬Ę B| = |A| ┬Ę |B|
- 12. 6. El rang d'una matriu A= ( 1 0 ŌłÆ2 3 4 1 2 2 ŌłÆ5 ŌłÆ2 3 1)Exemple: 1r pas: Buscar un menor d'ordre 2 diferent de 0 E7,E8,E9 p32: 15 A= ( 1 0 ŌłÆ2 3 4 1 2 2 ŌłÆ5 ŌłÆ2 3 1) |1 0 4 1|=1 ŌēĀ 0 Rang Ōēź 2 2n pas: Buscar un menor d'ordre 3 diferent de 0 ŌłŻ 1 0 ŌłÆ2 4 1 2 ŌłÆ5 ŌłÆ2 3 ŌłŻ=13 ŌēĀ 0 Rang = 3 ├ēs el nombre de files/columnes no nul┬Ęles linealment independents. Coincideix amb l'ordre del menor m├®s gran diferent de zero de la matriu.
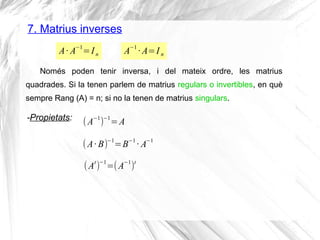
- 13. 7. Matrius inverses Nom├®s poden tenir inversa, i del mateix ordre, les matrius quadrades. Si la tenen parlem de matrius regulars o invertibles, en qu├© sempre Rang (A) = n; si no la tenen de matrius singulars. A┬Ę AŌłÆ1 =In -Propietats: AŌłÆ1 ┬Ę A=I n (AŌłÆ1 )ŌłÆ1 =A (A┬Ę B)ŌłÆ1 =BŌłÆ1 ┬Ę AŌłÆ1 (At )ŌłÆ1 =(AŌłÆ1 )t
- 14. Matriu dels adjunts: Ex d'ordre 3, 21 AŌłÆ1 = 1 ŌłŻAŌłŻ ┬Ę Adj(A)t A= ( a11 a12 ... a1n a21 a22 ... a2n ... ... ... ... am1 am2 ... amn ) Adj(A)= ( m11 m12 ... m1n m21 m22 ... m2n ... ... ... ... mm1 mm2 ... mmn ) Matriu inversa: E10,E11, p35: 19,21,23 Activitats finals: 1,3,5,6,9,10,11,12,15,16,17,18,20,24 -C├Ālcul de la inversa d'una matriu:
- 15. 3. El rang d'una matriu El rang d'una matriu ├®s el nombre de files no nul┬Ęles linealment independents. Sempre coincideix amb el nombre de columnes. A=(5 ŌłÆ3 4 10 ŌłÆ6 8) Exemples: B=(ŌłÆ4 ŌłÆ4 0 0 3 ŌłÆ3)Rang(A) = 1 Rang(B) = 2 C= ( 2 0 3 ŌłÆ4 3 ŌłÆ5 2 3 8 ŌłÆ10 7 2 ) Rang(C) = 2 Ja que F1 = -2F2 + F3 No ├®s immediat! M├łTODE DE GAUSS
- 16. Consisteix en transformar la matriu de tal manera que quedin 0 sota la diagonal. El rang ser├Ā el nombre de files no nul┬Ęles. M├©tode de Gauss per calcular el rang d'una matriu: A= ( 0 ŌłÆ2 2 4 2 ŌłÆ1 ŌłÆ1 1 2 ŌłÆ2 0 3) 1r pas: Primera columna tot 0's menys la primera fila F3 ŌĆō F1( 2 ŌłÆ1 ŌłÆ1 1 0 ŌłÆ2 2 4 2 ŌłÆ2 0 3) ( 2 ŌłÆ1 ŌłÆ1 1 0 ŌłÆ2 2 4 0 ŌłÆ1 1 2)Canvi fila 2n pas: Segona columna tot 0's menys la primera i segona files ( 2 ŌłÆ1 ŌłÆ1 1 0 ŌłÆ2 2 4 0 0 0 0)2F3 ŌĆō F2 Rang(A) = 22 files no nul┬Ęles p18 21, 22, 23, 24, 92, 93, 94
- 17. 4. Matrius inverses Trobar la matriu inversa: el m├©tode de Gauss-Jordan. A= ( 2 ŌłÆ1 2 4 ŌłÆ3 ŌłÆ1 ŌłÆ6 4 ŌłÆ2) ( 2 ŌłÆ1 2 1 0 0 4 ŌłÆ3 ŌłÆ1 0 1 0 ŌłÆ6 4 ŌłÆ2 0 0 1) ( 2 ŌłÆ1 2 1 0 0 0 ŌłÆ1 ŌłÆ5 ŌłÆ2 1 0 0 1 4 3 0 1) 1r pas: Primera columna tot 0's menys la primera fila, segona columna tot 0's menys segona fila, i aix├Ł successivament fins que quedi una matriu diagonal. F3 + 3F1 (a11=0) F2 ŌĆō 2F1 ( 2 0 7 3 ŌłÆ1 0 0 ŌłÆ1 ŌłÆ5 ŌłÆ2 1 0 0 0 ŌłÆ1 1 1 1)F3 + F2 F1 ŌĆō F2 ( 2 0 0 10 6 7 0 ŌłÆ1 0 ŌłÆ7 ŌłÆ4 ŌłÆ5 0 0 ŌłÆ1 1 1 1 )F2 - 5F3 F1 + 7F3
- 18. ( 2 ŌłÆ1 2 1 0 0 0 ŌłÆ1 ŌłÆ5 ŌłÆ2 1 0 0 1 4 3 0 1) 1r pas: Primera columna tot 0's menys la primera fila, segona columna tot 0's menys segona fila, i aix├Ł successivament fins que quedi una matriu diagonal. F3 + 3F1 F2 ŌĆō 2F1 ( 2 0 7 3 ŌłÆ1 0 0 ŌłÆ1 ŌłÆ5 ŌłÆ2 1 0 0 0 ŌłÆ1 1 1 1)F3 + F2 F1 ŌĆō F2 ( 2 0 0 10 6 7 0 ŌłÆ1 0 ŌłÆ7 ŌłÆ4 ŌłÆ5 0 0 ŌłÆ1 1 1 1 )F2 - 5F3 F1 + 7F3 2n pas: Quan la matriu inicial est├Ā en format diagonal, la transformem en la matriu identitat. ( 1 0 0 5 3 7/2 0 1 0 7 4 5 0 0 1 ŌłÆ1 ŌłÆ1 ŌłÆ1 )- F2 1/2F1 - F3 p21 28, 29
- 19. 5. Equacions matricials a) Tipus AX = B AX =B Identitat A ŌłÆ1 ┬Ę AX =A ŌłÆ1 ┬Ę B X =A ŌłÆ1 ┬Ę B b) Tipus XA = B XA=B Identitat XA┬Ę A ŌłÆ1 =B┬Ę A ŌłÆ1 X =B┬Ę A ŌłÆ1 c) Tipus AX + B = C AX +B=C Identitat AŌłÆ1 ┬Ę AX =AŌłÆ1 ┬Ę(CŌłÆB) X =AŌłÆ1 ┬Ę(CŌłÆB) AX =CŌłÆB p22 SF, 30, 31, 32, 33, operaci├│ sele10