0124 1 linear_algebra_basic_vector
- 1. 2018 FASTCAMPUS Extension SCHOOL FAST CAMPUS SCHOOL 2018 Copyright FAST CAMPUS Corp. All Rights Reserved ê¸°ì´ ì íëì (벡í°) ì¤ ì í
- 2. 2018 FASTCAMPUS Extension SCHOOL Vectorë? â Data를 ë¶ìí ë, Vector를 ì ë°°ì°ëê°? â ì íµì ì¸ ì íëìíììë 벡í°ë¥¼ ì«ìë¤ì listë¡ ìê°íëë¡ íë¤. â ì¬ë¬¼ì listë¡ íííì¬ ë°ì´í°í í ì ìë¤. ⸠ì¬ëì (í¤, 몸무ê², ëì´)ë¡ êµ¬ì±ë listë¡ ííí ì ìë¤. ⸠íìì ìí ì±ì ì (ìí 1 ì ì, ìí 2 ì ì, ìí 3 ì ì, ìí 4 ì ì)ì listë¡ íííë¤. â 벡í°ë¡ ííë ë°ì´í°ë ê³ì°í기 ì½ë¤. â pythonì list를 ì¬ì©íì¬ ë²¡í°ë¥¼ ëíë¼ ì ìë¤. ⸠python ìì ì½ë를 ë³´ì
- 3. 2018 FASTCAMPUS Extension SCHOOL Vectorì ì ì â Vectorì ìíì ì ì â Scalaë 물리ìì ííëë 물리ì ì¸ ì(Quantity)ì¼ë¡ì, ìì¹ê°ì¼ë¡ ìì íê² íìí ì ìë ìì´ë¤. ⸠배ì ìë ¥ì 10ë ¸í¸ â Vectorë 물리ìì ííëë 물리ì ì¸ ì(Quantity)ì¼ë¡ì, ìì¹ê°ê³¼ ë°©í¥ì±ì´ ìì´ì¼ ìì íê² íìí ì ìë ìì´ë¤. ⸠배ì ìëë ëì¹¨ë° ììì 45ë ë¶ëë°©í¥ì¼ë¡ 10ë ¸í¸
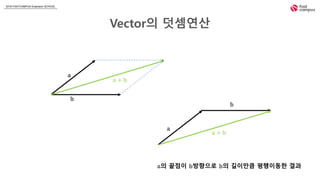
- 4. 2018 FASTCAMPUS Extension SCHOOL Vectorì ë§ì ì°ì° ð ð ð + ð ð ð ð + ð ðì ëì ì´ ðë°©í¥ì¼ë¡ ðì 길ì´ë§í¼ ííì´ëí ê²°ê³¼
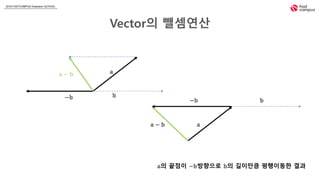
- 5. 2018 FASTCAMPUS Extension SCHOOL Vectorì ëºì ì°ì° ð ð ð â ð ð ð ð â ð ðì ëì ì´ âðë°©í¥ì¼ë¡ ðì 길ì´ë§í¼ ííì´ëí ê²°ê³¼ âð âð
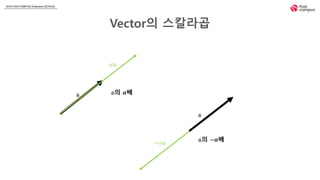
- 6. 2018 FASTCAMPUS Extension SCHOOL Vectorì ì¤ì¹¼ë¼ê³± ð ð¼ð ð âð¼ð ðì ð¶ë°° ðì âð¶ë°°
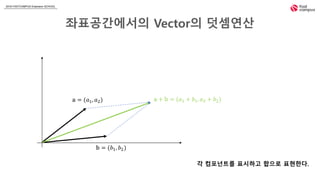
- 7. 2018 FASTCAMPUS Extension SCHOOL ì¢íê³µê°ììì Vector â íì´íê° ë²¡í°ë¥¼ 기ííì ì¼ë¡ íííë ë° ì ì©íë¤. â ì°ë¦¬ë 벡í°ë¥¼ ëìì ì¼ë¡ íííë ¤ê³ íê³ ì§êµì¢íê³ì 벡í°ê° ìë ê²ì¼ë¡ ìê°íë¤. â ì§êµì¢íê³µê°ìì íì ì ð¥ì¶, ð¦ì¶ ⦠ì ìììê³¼ 1:1ëìì´ ì´ë£¨ì´ì§ë¤. ìììì ìë ì¢í를 ì±ë¶(component)ì´ë¼ê³ ë¶ë¥¸ë¤. â 벡í°ë ì´ë¤ ì íí ì°¨ìì ê³µê°ì ì¡´ì¬íë ì ë¤ì´ë¤. â ë°ë¼ì ì«ìë¡ êµ¬ì±ë listë¡ ííí ì ìë¤.
- 8. 2018 FASTCAMPUS Extension SCHOOL ì¢íê³µê°ììì Vectorì ë§ì ì°ì° ê° ì»´í¬ëí¸ë¥¼ íìíê³ í©ì¼ë¡ íííë¤. ð = (ð1, ð2) ð = (ð1, ð2) ð + ð = (ð1 + ð1, ð2 + ð2)
- 9. 2018 FASTCAMPUS Extension SCHOOL ì¢íê³µê°ììì Vector ì°ì° â ì¢êµê³µê°ììì vector ì°ì°ì ì¢ ë¥ â ðì°¨ì ì¤ìê³µê° ð ðë´ì ë ë²¡í° ð§ = (ð£1, ⦠, ð£ ð), ð¨ = (ð¤1, ⦠, ð¤ ð)ì ììì ì¤ì¹¼ë¼ ðì ëíì¬ â¸ ð§ + ð¨ = ð£1 + ð¤1, ⦠, ð£ ð + ð¤ ð ⸠ðð§ = ðð£1, ⦠, ðð£ ð ⸠âð§ = âð£1, ⦠, âð£ ð ⸠ð¨ â ð§ = (ð¤1 â ð£1, ⦠, ð¤ ð â ð£ ð)
- 10. 2018 FASTCAMPUS Extension SCHOOL ì¢íê³µê°ììì Vector ì°ì° â ì¢íê³µê°ììì vectorì ì°ì°ì ì±ì§ â ð¦, ð§, ð¨ : 벡í°, ð, ð : ì¤ì¹¼ë¼ ⸠êµíë²ì¹ ð¦ + ð§ = ð¦ + ð§ ⸠결í©ë²ì¹ ð¦ + ð§ + ð¨ = ð¦ + ð§ + ð¨ ⸠íë±ì ð¦ + ð = ð + ð¦ ⸠ìì ð¦ + âð¦ = ð ⸠ð + ð ð¦ = ðð¦ + ðð¦ ⸠ð ð¦ + ð§ = ðð¦ + ðð§ ⸠ð ðð¦ = ðð ð¦ ⸠1ð¦ = ð¦ ⸠0ð§ = ð ⸠ðð = ð ⸠â1 ð§ = âð§
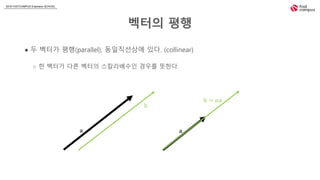
- 11. 2018 FASTCAMPUS Extension SCHOOL 벡í°ì íí â ë 벡í°ê° íí(parallel), ëì¼ì§ì ìì ìë¤. (collinear) â í 벡í°ê° ë¤ë¥¸ 벡í°ì ì¤ì¹¼ë¼ë°°ìì¸ ê²½ì°ë¥¼ ë»íë¤. ð ð = ð¼ð ð ð
- 12. 2018 FASTCAMPUS Extension SCHOOL Vectorì ì¼ì°¨ê²°í© â Vectorì ì¼ì°¨ê²°í© (Linear Combination) â ð¨, ð§1, ⦠, ð§ ð â ð ð, ì¤ì¹¼ë¼ ð1, ⦠, ð ðê° ì£¼ì´ì¡ì ë, ë²¡í° ð¨ê° ð¨ = ð1 ð§1 + ð2 ð§2 + ⯠+ ð ð ð§ ðë¡ íí ëë©´, ë²¡í° ð¨ë ë²¡í° ð§1, ð§2, ⦠, ð§ ðì 1ì°¨ ê²°í©ì´ë¼ê³ íë¤. â ì´ ë ð1, ð2, ⦠, ð ðë ê³ì(coefficient)ë¼ê³ íë¤.
- 13. 2018 FASTCAMPUS Extension SCHOOL Row vector / Column vector â ê´í¸í기(comma-delimited)ë¡, ð ðì ì¢íê³µê°ë´ììì ë²¡í° í기 ð§ = ð£1, ⦠, ð£ ð â 벡í°í기ë ðê°ì ì±ë¶(component)를 ì í´ì§ ììë¡ ëì´ëì ê²ì´ê¸° ë문ì, 벡í°ì ì± ë¶ì ì¬ë°ë¥¸ ììëë¡ ì ì´ ì£¼ë ì´ë í íìì í기방ìì´ë¼ë ê´í¸í기를 ëì í ì ìë¤. â ð§ = [ð£1, ð£2, ⦠, ð£ ð]ì íë²¡í° íìì´ë¼ê³ íë¤. (row vector) â ð§ = ð£1, ð£2, ⦠, ð£ ð ð = ð£1 ð£2 â® ð£ ð 를 ì´ë²¡í° íìì´ë¼ê³ íë¤. (column vector)
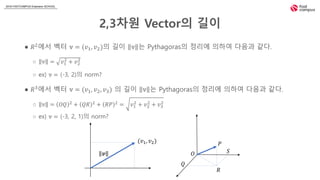
- 14. 2018 FASTCAMPUS Extension SCHOOL 2,3ì°¨ì Vectorì ê¸¸ì´ â ð 2ìì ë²¡í° ð§ = (ð£1, ð£2)ì ê¸¸ì´ ð§ ë Pythagorasì ì 리ì ìíì¬ ë¤ìê³¼ ê°ë¤. â ð§ = ð£1 2 + ð£2 2 â ex) ð§ = (-3, 2)ì norm? â ð 3ìì ë²¡í° ð§ = (ð£1, ð£2, ð£3) ì ê¸¸ì´ ð§ ë Pythagorasì ì 리ì ìíì¬ ë¤ìê³¼ ê°ë¤. â ð§ = ðð 2 + ðð 2 + ð ð 2 = ð£1 2 + ð£2 2 + ð£3 2 â ex) ð§ = (-3, 2, 1)ì norm? (ð£1, ð£2) ð ð ð ð ð ð
- 15. 2018 FASTCAMPUS Extension SCHOOL ðì°¨ì Vectorì ê¸¸ì´ â ð§ = (ð£1, ð£2, ⦠, ð£ ð)ì´ ð ðì 벡í°ì´ë©´ ð§ì 길ì´(length ëë norm) í¹ì í¬ê¸°(magnitude)ë ð§ ë¡ íìíë©° ë¤ìê³¼ ê°ì´ ì ìíë¤. â ð§ = ð£1 2 + ð£2 2 + ⯠+ ð£ ð 2 â ë²¡í° ð§ â ð ðì ììì ì¤ì¹¼ë¼ ðì ëíì¬, â ð§ ⧠0 â ð§ = 0ì´ ë기 ìí íì충ë¶ì¡°ê±´ì ð§ = 0ì´ë¤. â ðð§ ⧠ð ð§
- 16. 2018 FASTCAMPUS Extension SCHOOL ë¨ì ë²¡í° â ë¨ì 벡í°(unit vector) â 길ì´ê° 1ì¸ ë²¡í°ë¥¼ ë¨ì벡í°ë¼ê³ íë¤. â ìì´ ìë ë²¡í° ð§ â ð ðì ê°ì ë°©í¥ì ê°ë ë¨ìë²¡í° ð¦ë ë¤ì ìì¼ë¡ 구íë¤. ð¦ = 1 ð§ ð§ â ë¨ì벡í°ë¥¼ 구íë ê³¼ì ì ì ê·í(normalizing)ë¼ íë¤. ex) v = (2, 2, -1)ì ë¨ì벡í°ë? 길ì´ê° 1ì¸ ë¨ìë²¡í° ð¦
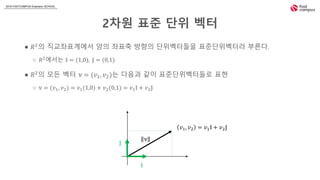
- 17. 2018 FASTCAMPUS Extension SCHOOL 2ì°¨ì íì¤ ë¨ì ë²¡í° â ð 2ì ì§êµì¢íê³ìì ìì ì¢íì¶ ë°©í¥ì ë¨ì벡í°ë¤ì íì¤ë¨ì벡í°ë¼ ë¶ë¥¸ë¤. â ð 2 ììë ð = (1,0), ð = (0,1) â ð 2ì 모ë ë²¡í° ð§ = (ð£1, ð£2)ë ë¤ìê³¼ ê°ì´ íì¤ë¨ì벡í°ë¤ë¡ íí â ð§ = (ð£1, ð£2) = ð£1(1,0) + ð£2(0,1) = ð£1 ð + ð£2 ð ð£1, ð£2 = ð£1 ð + ð£2 ð ð§ ð ð
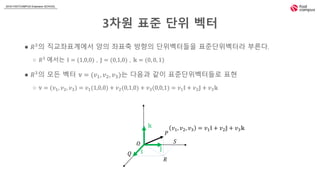
- 18. 2018 FASTCAMPUS Extension SCHOOL 3ì°¨ì íì¤ ë¨ì ë²¡í° â ð 3ì ì§êµì¢íê³ìì ìì ì¢íì¶ ë°©í¥ì ë¨ì벡í°ë¤ì íì¤ë¨ì벡í°ë¼ ë¶ë¥¸ë¤. â ð 3 ììë ð = (1,0,0) , ð = (0,1,0) , ð = (0, 0, 1) â ð 3ì 모ë ë²¡í° ð§ = (ð£1, ð£2, ð£3)ë ë¤ìê³¼ ê°ì´ íì¤ë¨ì벡í°ë¤ë¡ íí â ð§ = (ð£1, ð£2, ð£3) = ð£1(1,0,0) + ð£2(0,1,0) + ð£3(0,0,1) = ð£1 ð + ð£2 ð + ð£3 ð ð ð ð ð ð ð ð ð ð£1, ð£2, ð£3 = ð£1 ð + ð£2 ð + ð£3 ð
- 19. 2018 FASTCAMPUS Extension SCHOOL ðì°¨ì íì¤ ë¨ì ë²¡í° â ì¼ë°ì ì¼ë¡ ð ðììì íì¤ë¨ì벡í°ë â ð1 = (1,0, ⦠, 0) , ð2 = (0,1, ⦠, 0) , ⦠, ð ð = 0,0, ⦠, 1 â ð ðì ë²¡í° ð§ = (ð£1, ð£2, ⦠, ð£ ð)ê° ë¤ìê³¼ ê°ì´ íì¤ë¨ì벡í°ë¤ë¡ì¨ ííë ì ìë¤. â ð§ = (ð£1, ⦠, ð£ ð) = ð£1 ð1 + ð£2 ð2 + ⯠+ ð£ ð ð ð â ì¦, 벡í°ê° íì¤ë¨ì벡í°ì ì íê²°í©(linear combination)ì¼ë¡ ëíë´ì´ì§ë¤.
- 20. 2018 FASTCAMPUS Extension SCHOOL 2,3ì°¨ìì ì ë¤ ê°ì 거리 â ð1ê³¼ ð2ê° ð 2ëë ð 3ì¬ì´ì ì ì´ë©´ ë²¡í° ð1, ð2ì 길ì´ë ë ì ê° ê±°ë¦¬ ðì ì¼ì¹íë¤. â 2ì°¨ì : ð(ð¦, ð§) = ||ð1 ð2|| = ð¥1 â ð¥2 2 + ð¦1 â ð¦2 2 â 3ì°¨ì : ð(ð¦, ð§) = ||ð1 ð2|| = ð¥1 â ð¥2 2 + ð¦1 â ð¦2 2 + (ð§1 â ð§2) ð1 ð2 ð = ||ð1 ð2||
- 21. 2018 FASTCAMPUS Extension SCHOOL ðì°¨ìì ì ë¤ ê°ì 거리 â ð¦ = (ð¢1, ð¢2, ⦠, ð¢ ð) , ð§ = (ð£1, ð£2, ⦠, ð£ ð)ì´ ð ðì ì ì´ë©´ ì´ë¤ ð¦ì ð§ì¬ì´ì 거리(distance)를 ð(ð¦, ð§)ë¡ íìíë©° ë¤ìê³¼ ê°ì´ ì ìíë¤. â ð(ð¦, ð§) = ð¦ â ð§ = ð¢1 â ð£1 2 + ð¢2 â ð£2 2 + ⯠+ (ð¢ ð â ð£ ð) ex) ð¦ = (1, 3, â2, 7) , ð§ = (0, 7, 2, 2) ë ì ì¬ì´ì 거리ë? â 거리ì ì±ì§ â ð ð¦, ð§ ⥠0 â ð(ð¦, ð§) = 0ì´ ë기 ìí íì충ë¶ì¡°ê±´ì ð¦ = ð§ì´ë¤. â ð(ð¦, ð§) = ð(ð§, ð¦)
- 22. 2018 FASTCAMPUS Extension SCHOOL 벡í°ì ë´ì â 벡í°ì ë´ì (Inner product)ì ë ë²¡í° ì¬ì´ì ê°ì ì¬ê±°ë ë 벡í°ê° ìë¡ ìì§ì´ë¼ë ê² ì íë³íëë° ì ì©í ê³±ì â ð¦ = (ð¢1, ⦠, ð¢ ð)ê³¼ ð§ = (ð£1, ⦠, ð£ ð)ì´ ð ðì 벡í°ì¼ë, ð¦ì ð§ì ì ê³±(dot product) ëë ð¦ì ð§ì Euclid ë´ì (Euclidean inner product)ì ð¦ â ð§ë¡ í기íë©° ë¤ì ìê³¼ ê°ì´ ì ìíë¤. â ð¦ â ð§ = ð¢1 ð£1 + ð¢2 ð£2 + ⯠+ ð¢ ð ð£ ð ex) ð¦ = (â1,3,5,7) , ð§ = (5, â4,7,0)
- 23. 2018 FASTCAMPUS Extension SCHOOL ë´ì ì ì±ì§ â ð§ = ð£1, ð£2, ⦠, ð£ ð â ð§ã»ð§ = ð£1 ð£1 + ð£2 ð£2 + ⯠+ ð£ ð ð£ ð = ð§ 2 â ë´ì ì 기본 ì±ì§ë¤ â ð¦, ð§, ð¨ê° ð ð ì 벡í°ì´ê³ ðê° ì¤ìì´ë©´ ⸠ð¦ã»ð§ = ð§ã»ð¦(ëì¹ì±) ⸠ð¦ã» ð§ + ð¨ = ð¦ã»ð§ + ð§ã»ð¨(ë¶ë°°ì±) ⸠ð ð¦ã»ð§ = ðð¦ ã»ð§ = ð¦ã»(ðð§) (ëì¹ì±) ⸠ð§ã»ð§ ⥠0 ì´ê³ ð§ã»ð§ = 0ì íì충ë¶ì¡°ê±´ì ð§ = 0 (ììì±) ⸠ðã»ð§ = ð§ã»ð ⸠ð§ + ð¦ ã»ð¨ = ð§ã»ð¨ + ð¦ã»ð¨ ⸠ð¦ã» ð§ â ð¨ = ð¦ã»ð§ â ð§ã»ð¨ ⸠ð§ â ð¦ ã»ð¨ = ð§ã»ð¨ â ð¦ã»ð¨
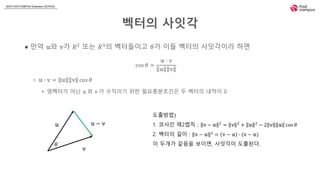
- 24. 2018 FASTCAMPUS Extension SCHOOL 벡í°ì ì¬ìê° â ë§ì½ ð¦ì ð§ê° ð 2 ëë ð 3ì 벡í°ë¤ì´ê³ ðê° ì´ë¤ 벡í°ì ì¬ìê°ì´ë¼ íë©´ cos ð = ð¦ â ð§ ð¦ ð§ â ð¦ â ð§ = ð¦ ð§ cos ð ⸠ì벡í°ê° ìë ð¦ ì ð§ ê° ìì§ì´ê¸° ìí íì충ë¶ì¡°ê±´ì ë 벡í°ì ë´ì ì´ 0 ð¦ ð§ ð¦ â ð§ ëì¶ë°©ë²) 1. ì½ì¬ì¸ ì 2ë²ì¹ : ð§ â ð¦ 2 = ð§ 2 + ð¦ 2 â 2 ð§ ð¦ cos ð 2. 벡í°ì ê¸¸ì´ : ð§ â ð¦ 2 = ð§ â ð¦ â (ð§ â ð¦) ì´ ëê°ê° ê°ìì ë³´ì´ë©´, ì¬ìê°ì´ ëì¶ëë¤.ð
- 25. 2018 FASTCAMPUS Extension SCHOOL 벡í°ì ì§êµ â ð ðì ë²¡í° ð¦ì ð§ê° ì§êµíë¤(orthogonal)ë ê²ì ð¦ â ð§ = 0ì ë§ì¡±ìí¤ë ê²½ì°ë¥¼ ë§íë¤. â ê³µì§í©ì´ ìë ð ðì 벡í°ë¤ì ì§í©ì´ ì§êµì§í©(orthogonal set)ì´ë¼ë ê²ì ì´ ì§í©ì ì ìì ìë¡ ë¤ë¥¸ í ìì 벡í°ê° ì§êµíë ê²ì ë§íë¤. ex) ë¤ì 벡í°ë¤ì´ ð 4ìì ì§êµì§í©ì ì´ë£¨ê³ ììì ë³´ì¬ë¼. ð§1 = (1,2,2,4) , ð§2 = (â2,1, â4,2) , ð§3 = (â4,2,2, â1)
- 26. 2018 FASTCAMPUS Extension SCHOOL 벡í°ì ì ê·ì§êµ â ð ðì ë ë²¡í° ð¦ì ð§ê° ì ê·ì§êµ(orthonormal)ë¼ë ê²ì ì´ë¤ì´ ì§êµíê³ ê¸¸ì´ê° 1ì¸ ê²½ ì°ë¥¼ ë»íë¤. â ð¦ â ð§ = 0 â ð¦ = 1, ð§ = 1 â 벡í°ë¤ì ì§í©ì´ ì ê·ì§êµì§í©(orthonormal set)ì´ë¼ë ê²ì ì´ ì§í©ì 모ë 벡í°ë¤ì 길 ì´ê° 1ì´ê³ ì´ ì§í© ìì ìë¡ ë¤ë¥¸ ììì í ìì 벡í°ë¤ì´ ì§êµíë ê²½ì°ë¥¼ ë»íë¤. ex) íì¤ë¨ìë²¡í° ð1 = (1,0, ⦠, 0) , ð2 = (0,1, ⦠, 0) , ⦠, ð ð = (0, ⦠, 0,1) ex) ë¤ìì´ ì ê·ì§êµì§í©ì ì´ë£¨ë ê²ì ë³´ì¬ë¼. ð¢1 = ( 1 5 , 2 5 , 2 5 , 4 5 ) , ð¢2 = (â 2 5 , 1 5 , â 4 5 , 2 5 ) , ð¢3 = (â 4 5 , 2 5 , 2 5 , â 1 5 )








![2018 FASTCAMPUS Extension SCHOOL
Row vector / Column vector
â ê´í¸í기(comma-delimited)ë¡, ð
ðì ì¢íê³µê°ë´ììì ë²¡í° í기 ð§ = ð£1, ⦠, ð£ ð
â 벡í°í기ë ðê°ì ì±ë¶(component)를 ì í´ì§ ììë¡ ëì´ëì ê²ì´ê¸° ë문ì, 벡í°ì ì±
ë¶ì ì¬ë°ë¥¸ ììëë¡ ì ì´ ì£¼ë ì´ë í íìì í기방ìì´ë¼ë ê´í¸í기를 ëì í ì
ìë¤.
â ð§ = [ð£1, ð£2, ⦠, ð£ ð]ì íë²¡í° íìì´ë¼ê³ íë¤. (row vector)
â ð§ = ð£1, ð£2, ⦠, ð£ ð
ð
=
ð£1
ð£2
â®
ð£ ð
를 ì´ë²¡í° íìì´ë¼ê³ íë¤. (column vector)](https://image.slidesharecdn.com/01241linearalgebrabasicvector-181005062403/85/0124-1-linear_algebra_basic_vector-13-320.jpg)