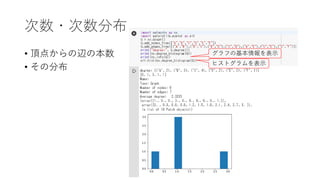
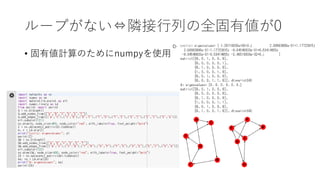
Introduction of network analysis with Google Colaboratory -- Network Metrics
- 2. データ構造:辺リスト ? 頂点ペアの列挙 頂点:A, …, F 辺:A-B,B-C, …
- 4. matplotlibでの描画 ? さまざまな描画を並べる matplotlibのライブラリを使用 横1列に3個描画、その1番目 頂点をランダムに配置 頂点を円周上に配置 頂点をばねモデルで配置
- 9. 共引用の計算 ? A:ネットワークの隣接行列 ? AT:その転置行列 ? ATAの対角成分を0としたもの が共引用の隣接行列 転置行列 行列の積 対角成分を 0に
- 13. 連結?連結成分 ? 連結:グラフ上の任意の2頂点間のパスが存在 ? 連結成分の個数:グラフラプラシアンの固有値 が0となるものの個数 ? = ? ? ? ? ? 1 = 0 ? 1各頂点の次数を成分 とする対角行列 少なくとも1つの固 有値0をもつ 隣接行列
- 14. クラスタ係数 ? (ある人の)友達2人が友達同士 である割合(値の範囲は0から1) ? 完全グラフ:クラスタ係数は1 ? 2部グラフ:クラスタ係数は0 ? 社会ネットワークでは比較的大 きな値をとる ?
- 15. 中心性 ? どれが最も中心? ? 赤 ? 青 ? 緑 ? 水色 ? 黄色
- 16. いろいろな中心性 ? どれが最も中心? ? 次数中心性 ? 固有ベクトル中心性 ? 近接中心性 ? 媒介中心性