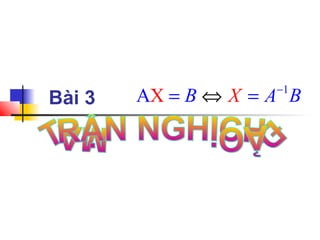03 matrannghichdao
- 1. Bài 3 1 AX XB A B− ⇔= =
- 2. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ta xét hệ phương trình: 2 3 8 2 3 8 5 7 1 5 7 1 x x y y x y + =       = ⇔       + =       Hệ phương trình trên có thể viết ở dạng ma trận: A X=B. Câu hỏi đặt ra là X = ?
- 3. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo )0(. 1 1 ≠=== − abab aa b x 1 .AX B X A B− = ⇔ = Xét phương trình: a x = b. Ta có: Tương tự lập luận trên thì liệu ta có thể có như vậy là ma trận sẽ được định nghĩa như thế nào? 1− A
- 4. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo bax bax baaxa bxa 1 1 11 1 − − −− =⇔ =⇔ =⇔ = 1 1 1 1 A X B A A X A B I X A B X A B − − − − = ⇔ = ⇔ = ⇔ = Ta để ý: Phải chăng ?1 IAA =−
- 5. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo
- 6. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo
- 7. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo Nhận xét:
- 8. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo Nhận xét:
- 9. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo
- 10. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo
- 11. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo
- 12. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo
- 13. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ví dụ: Tìm ma trận phụ hợp của ma trận sau: 1 2 3 2 4 0 4 5 7 A    = −   −  11A = 28 12A = 14 13A = -6 21A = -29 22A = -5 23A = 13 31A = -12 32A = -6 33A = 8 11 21 31 12 22 32 13 23 33 A A A A P A A A A A A        = =          
- 14. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Bài tập: Tìm ma trận phụ hợp của ma trận sau: 2 0 0 5 1 0 3 4 1 A    =    −  11A = -1 12A = 5 13A = 17 21A = 0 22A = -2 23A = -8 31A = 0 32A = 0 33A = 2 11 21 31 12 22 32 13 23 33 A A A A P A A A A A A        = =          
- 15. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo
- 16. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo 1 2 3 28 29 12 2 4 0 14 5 6 4 5 7 6 13 8 AAP − −       = − − −       − −    38 0 0 0 38 0 0 0 38    =      Ví dụ: 1 0 0 38 0 1 0 0 0 1    =     
- 17. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo
- 18. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ví dụ: 1 28 29 12 1 14 5 6 38 6 13 8 A− − −   = − −   − 
- 19. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ví dụ: Tìm ma trận nghịch đảo của ma trận sau: 1 2 3 0 1 4 0 0 1 A    =    −  det( ) 1A = − 1 2 5 0 1 4 0 0 1 −   − −     1 2 5 0 1 4 0 0 1 − −       − AP = 1 A− =
- 20. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ví dụ: Tìm ma trận nghịch đảo của ma trận sau: 2 6 1 4 A   =     det( ) 2A = 4 6 1 2 −   −  1 2 2 34 61 11 22 −−    =    −−    AP = 1 A− =
- 21. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Bài tập: Tìm ma trận nghịch đảo của ma trận sau: 0 2 3 1 0 1 4 5 0 A    = −     1 det( ) ? 1 ? det( ) A A A A P P A − =  ⇒ = = 
- 22. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Đáp số: 1 5 15 2 1 4 12 3 7 5 8 2 A− −   = − −   − 
- 23. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Bài tập: Tìm ma trận nghịch đảo của ma trận sau: 2 5 1 2 A   =     Chú ý: Đối với ma trận vuông cấp 2 A a b d b A P c d c a −    = ⇒ =   −    Đáp số: 1 2 5 1 2 A− −  =  − 
- 24. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo Bài toán:Bài toán: Tìm ma trận X thỏa mãnTìm ma trận X thỏa mãn 1)1) AX = BAX = B 2)2) XA = BXA = B 3)3) AXB = CAXB = C 4)4) AX + kB = CAX + kB = C
- 25. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ta có: 1 -1 -1 -1 1) AX=B A AX=A IX=A B A B X B− = ⇔ ⇔ ⇔ 1 1 1 1 2) XA B XAA BA XI BA X BA − − − − = ⇔ = ⇔ = = ⇔ 1 A B− ≠
- 26. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ta có: -1 -1 -1 -1 1 1 1 3) AXB=C A AXB=A XBB =A X A B CB C C − − − = ⇔ ⇔ ⇔ 1 1 1 ( 4 ( ) ( ) ) ) AX kB C AX C kB A AX A C kB X A C kB − − − + = ⇔ = − ⇔ = − ⇔ = −
- 27. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ví dụ: Dùng ma trận nghịch đảo giải hệ phương trìnhsau: 2 6 3 2 1 4 3 5 5 x y z x y z x y z + − =  − + = −  + + = 1 2 1 6 3 1 2 1 4 3 5 5 x y z −           ↔ − = −                 1 2 1 X    ⇒ =    −  1 AX B X A B− = ⇔ =
- 28. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ví dụ: Tìm ma trận X thỏa mãn: 1 2 3 1 5 0 1 4 0 4 0 0 1 2 3 X        =       −    Phương trình có dạng: AX=B 1 X A B− =Ta có:
- 29. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo 1 2 5 1 5 0 1 4 0 4 0 0 1 2 3 X − −       =        −    9 18 8 16 2 3 − −   =    − −  Vậy
- 30. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo 1 3 1 1 2 3 2 2 4 2 0 0 5 X − −      + =            2XA B C+ =  Ví dụ: Tìm ma trận X thỏa mãn: Phương trình có dạng 1 ( 2 )X C B A− ⇔ = −
- 31. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo  Ta có 1 ( 2 )X C B A− = − 1 4 3 0 11 ; 2 2 1 4 52 A C B− − −    = − − =   − −    0 1 4 3 0 1 4 31 1 ( ) 4 5 2 1 4 5 2 12 2 X − − − −        = − = −       − − − −        Với nên 1 2 17 2 12 11 1326 172 −−    = − =    −−   
- 32. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo 1 3 2 2 2 0 4 2 0 4 5 0 3 8 6 X − −       =       − −    AX B=  Bài tập: Tìm ma trận X thỏa mãn: Phương trình có dạng 1 X A B− ⇔ =
- 33. Gi¶ng viªn: Phan §øc TuÊn Đại Số Tuyến Tính ∑ Đại Số Tuyến Tính ∑ §3: Ma trận nghịch đảo 2 4 2 7 4 8 3 5 1 3 2 0 X       =     −      AXB C=  Bài tập: Tìm ma trận X thỏa mãn: Phương trình có dạng 1 1 X A CB− − ⇔ =