�ݺ�ߣ

Kapitulli 6: Kinematika e Fluideve
Altin DORRI
Elemente te Fluidodinamikes

Chapter 4: Fluid Kinematics
ME33 : Fluid Flow 2
Kinematika e fluideve
Trajton levizjen e fluideve pa marre parasysh forcat
qe shkaktojne ate.
Pra pershkruhen disa parametra te levizjes se nje
fluidi si pozicioni, shpejtesia dhe nxitimi, etj.
Ka nje rendesi themelore jo vetem per pershkrimin e
rrymes por edhe per vizualizimin (paraqitjen) e saj.
Menyrat e pershkrimit te levizjes (Langrazhiane &
Euleriane)
Elementet kryesore te levizjes
Format e levizjes se fluidit

ME33 : Fluid Flow 3
Pershkrimi Lagrangian
Konsiston ne ndjekjen e levizjes se te gjitha grimcave
te fluidit ne kohe duke ruajtur veçmas identitetin e tyre.
Bazohet ne ligjin e dyte te Njutonit.
Ka veshtiresi per analiza praktike, sepse:
Fluidet perbehen nga miliona molekula.
Ka veshtiresi pershkrimi dhe modelimi ne bashkeveprimin
mes molekulave.
Megjithate, i dobishem per perdorimi specifike
Sprajte, grimca, dinamika e bulezave, gazet e ralluar.
Metoda e kombinuar Euleriane-Lagrangiane.

ME33 : Fluid Flow 4
Pershkrimi Eulerian
Pershkruan levizjen e fluidit duke marre nje pike fikse ne hapesire
pamvaresisht nga grimcat qe kalojne ne te .
Parametrat e levizjes jane funksione te hapesires dhe kohes.
Fusha e presioneve, p=p(x,y,z,t)
Fusha e shpejtesive,
Fusha e nxitimit,
Keto parametra (dhe te tjere) percaktojne fushen e levizjes.
Shume e perdorshme ne probleme praktike.
Perfundimisht duke qene e pamundur identifikimi i grimcave te veçanta
fluide ne nje fluks, pershkrimi Langrazhian zakonisht nuk perdoret ne
praktike dhe pse nga ana teorike ka avantazhin se jep me shume
informacion te kuptueshem per madhesite fluidodinamike.
     
, , , , , , , , ,
V u x y z t i v x y z t j w x y z t k
  
     
, , , , , , , , ,
x y z
a a x y z t i a x y z t j a x y z t k
  
 
, , ,
a a x y z t

 
, , ,
V V x y z t


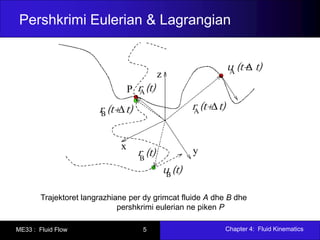
ME33 : Fluid Flow 5
Pershkrimi Eulerian & Lagrangian
Trajektoret langrazhiane per dy grimcat fluide A dhe B dhe
pershkrimi eulerian ne piken P

ME33 : Fluid Flow 6
Fusha e shpejtesise & nxitimit
Pergjithesisht grimcat e fluidit ne levizje kane shpejtesi dhe nxitim te
ndryshem. Per kete shqyrtojme trajektoren e grimces ne figuren poshte,
shohim se ne çastin t ze pozicionin r(t) ndersa ne momentin t + t ze
pozicionin r(t + t). atehere shpejtesia dhe nxitimi ne kohen t do te jepen nga
formulat:
Figura: Pozicioni, shpejtesia dhe nxitimi pergjate trajektores se nje grimce fluide

ME33 : Fluid Flow 7
Fusha e shpejtesise & nxitimit
Ne pershkrimin eulerian te nxitimit duhet marre parasysh ndryshimi i
shpejtesise ne piken fikse x te nje grimce fluide pozicioni se ciles ne
momentin t eshte pikerisht x. Pra kjo grimce do te kete nje pozicion x te varur
nga koha pra do te kete per nxitim:
Per te tre komponentet do te jete
z
u
u
y
u
u
x
u
u
t
u
a x
z
x
y
x
x
x
x












z
u
u
y
u
u
x
u
u
t
u
a
y
z
y
y
y
y
y
y












z
u
u
y
u
u
x
u
u
t
u
a z
z
z
y
z
x
z
z












Nxitimi lokal
Nxitimi konektiv

ME33 : Fluid Flow 8
Elementet e levizjes fluidit
Perkufizojme trajektoren (pathline) si vendin gjeometrik (lakore) qe
formohet nga bashkimi i vendndodhjeve te njepas-njeshme qe ze
grimca ne hapesire ne çastet e njepas-njeshme. Trajektorja eshte nje
koncept langrazhian perderisa eshte e lidhur me identifikimin e
grimcave te veçanta.
)
,
( t
r
u
dt
dr

Shprehja matematike e
trajektores

ME33 : Fluid Flow 9
Perkufizojme vijen e rrymes (streamlines) si vijen (lakoren) qe ne çdo
pike eshte tangente me vektorin lokal te shpejtesise. Koncepti i vijes se
rrymes eshte natyrisht nje koncept eulerian perderisa shqyrton ne çdo çast te
kohes shperndarjen hapesinore te shpejtesise, duke fiksuar nje bashkesi pikash.
Vijat e rrymes ne
dy çaste te
ndryshme kohe
dt
u
dz
u
dy
u
dx
u
u
dr
dr
z
y
x




 Shprehja matematike e
vijes se rrymes

ME33 : Fluid Flow 10
Perkufizojme vijat e emetimtit (streaklines) si vendin gjeometrik (lakorja) ne
te cilen jane vendosur ne nje çast te dhene kohe gjithe grimcate fluidit qe
kane dale nga nje pike e hapesires gjate nje intervali kohe. Ky koncept eshte
teper i perdorshem gjate vizualizimeve laboratorike ne rastet kur leshohet nje
gjurmelenes (tym) ne fluks nga nje pozicion fiks dhe ndiqen gjurmet e lena nga tymi
ne hapesire.

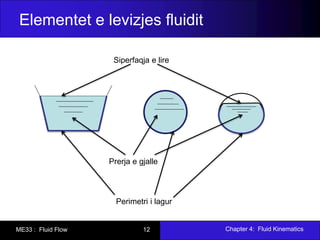
 Tubi i rrymes: vijat e rrymes qe kalojne neper nje lakore te mbyllur
Rrjedhje e fluidit quhet vellimi i fluidit qe leviz ne menyre te vazhduar
dhe qe kufizohet nga nje shtrat i ngurte.
Rryme fluidi quhet rrjedhja e fluidit e cila
kufizohet nga nje mjedis tjeter fluidi
(leng ose gas, psh shatervanet, zjarfikese).
Prerje e gjalle quhet prerja terthore e rrjedhjes normal me drejtimin e
levizjes
Perimetri lagur eshte gjatesia e perimetrit te prerjes se gjalle ne kufi me
shtratin e ngurte.
Prurje quhet sasia e fluidit qe rrjedh neper prerjen e gjalle ne njesine e
kohes.

Siperfaqja e lire
Prerja e gjalle
Perimetri i lagur

Krahasimi
Per levizje te qendrueshme, trajektorja, vija e rrymes
dhe ajo e emetimit perputhen.
Per levizje te paqendrueshme jane te ndryshme.
Vijat e rrymes kane karakter te castit
Trajektorja dhe vijat e emetimit shtrihen ne kohe.
Vija e emetimit: fotografi e castit e modelit te rrymes
integruar ne kohe
Trajektorja: karakter individual per cdo grimce.

Krahasimi
Metoda studimit
Menyra e
paraqitjes
Vijat e
rrymes
Sasi e madhe
grimcash te vogla
Film i shkurter
ose ekspozim i
gjate fotografie
Trajektorja
Vetem nje grimce
paraqitet
Film
Vijat e
emetimit
Te gjitha grimcat
dalin nga e njejta
pike
Fotografi

Format e levizjes
Ne mekaniken e fluideve levizja e
nje elemnt fluidi perbehte nga
kater forma baze:
a) Zhvendosese
b) Rotulluese
c) Deformuese lineare
d) Deformuese kendore
Levizja mund te shprehet me
mire ne termat e:
a) shpejtesise: shkalla e
zhvendosjes
b) Shpejtesia kendore: shkalla e
rotullimit
c) Shkalla e deformimit linear
d) Shkalla e deformimit kendor

Klasifikimi rrjedhjeve
Rrjedhje e qendrueshme: kur parametrat (densitet, presion,
shpejtesi, etj) e saj nuk jane funksion i kohes
Rrjedhje e paqendrueshme: kur parametrat e saj jane
funksion i kohes.
Rrjedhje e njetrajshme: kur nxitimet konektive jane zero
Rrjedhje e ndryshueshme: kur ndryshon prerja e gjalle gjate
levizjes.
Rrjedhje me presion: kur levizja shkaktohet nga ndryshimi
presionit ne dy anet e shtratit
Rrjedhje e lire (pa presion): kur levizja shkaktohet vetem nga
forca e rendeses.
Rrjedhje potenciale dhe rrjedhje shtjellore
Rrjedhje 1, 2 dhe 3 permasore

Funksioni rrymes
Rezulton e natyrshme te fusim kuptimin e funksionit te rrymes si ate funksion
izolinjat e te cilit (ne rastin dy dimensional ose izosiperfaqet per rastin tre dimensional)
perbejne vijat e rrymes.
duke marre keshtu qe pergjate nje vije rryme madhesia uxdy – uydx nuk ndryshon.
Neqoftese supozojme d = uxdy – uydx
do te kemi qe dhe funksioni  nuk ndryshon pergjate vijes se rrymes (prandaj quhet
dhe funksion i rrymes), pra eshte funksioni qe kerkonim.
Funksioni i rrymes gjen perdorim praktik kur duam te gjeme prurjen vellimore mes dy
pikave. Shqyrtojme elementin gjatesor ds te segmentit qe bashkon pikat A dhe B si ne
shembullin e figures
y
x u
dy
u
dx
  uxdy – uydx = 0

Funksioni rrymes
Do te kemi qe prurja elemntare ne te eshte dQ = unds = uxdy – uydx dhe ne baze te (2.11)
do te jete e barabarte me d. Atehere prurja mes A dhe B eshte: Q = 
B
A
dQ =
B
A
( uxdy – uydx) = 
B
A
d = B - A (2.12)
Keshtu pra nese njihet funksioni rrymes per nje fluks, diferenca e  mes dy pikave
çfaredo na jep vleren e prurjes ne vellim (per njesi te gjatesise ne drejtimin pingul me
fleten) qe kalon mes dy pikave. Shprehja (2.12) na tregon gjithashtu se vlera e prurjes
eshte e pavarur nga rruga e ndjekur per te shkuar nga A tek B pra d eshte nje diferencial
i sakte. Ne rastin kur A dhe B zgjidhen ne te njejten vije rryme kemi Q = 0. Pra eshte
konsistente me faktin qe nje vije rryme eshte gjithnje tangent me vektorin e shpejtesise
dhe keshtu ajo sillet si nje siperfaqe mushamaje ne te cilen vlera e prurjes eshte zero.

Potenciali shpejtesise
Do te perkufizojme: funksionin e kordinatave dhe kohes, diferencialet e pjesshem te
te cilit sipas kordinatave jane te barabarta me projeksionet perkates te shpejtesise.
Emertojme kete funksion  (x, y, z, t) atehere do te kemi:
z
u
y
u
x
u z
y
x












;
; (2.23)
Neqoftese shqyrtojme rastin dydimesional, supozojme qe egziston potenciali i
shpejtesise pra
y
u
x
u y
x








; dhe derivojme perkatesisht ne lidhje me y dhe x:
x
y
y
ux





 
2
dhe
y
x
x
uy





 
2
, meqenese vlera e derivatit te funksionit s’varet nga
forma e diferencimit atehere kemi:
x
u
y
u y
x





ose 0






x
u
y
u y
x
por kjo do te
thote nga (2.17) qe dhe  =0, pra nuk kemi levizje rrotulluese. Ky eshte dhe kuptimi
fizik dhe perdorimi praktik i potencialit te shpejtesise, qe kur ai egziston fluidi
(grimca) kryen levizje te paster zhvendosese (jorrotulluese).

�ݺ�ߣ

04_Kinematika_e_Fluideve.ppt

More Related Content

04_Kinematika_e_Fluideve.ppt