はじめてのパターン認識 第1章
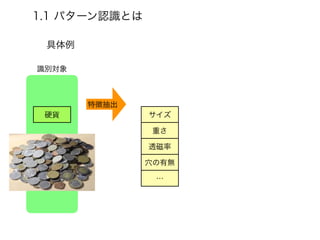
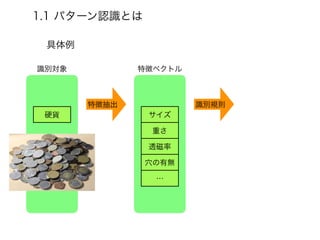
- 13. 1.1 パターン認識とは 識別対象 特徴ベクトル 特徴抽出 識別規則 サイズ 重さ 透磁率 穴の有無 … 硬貨 具体例
- 14. 1.1 パターン認識とは 識別対象 特徴ベクトル 識別クラス 特徴抽出 識別規則 サイズ 重さ 透磁率 穴の有無 … 10円 50円 100円 500円 識別不能 硬貨 具体例
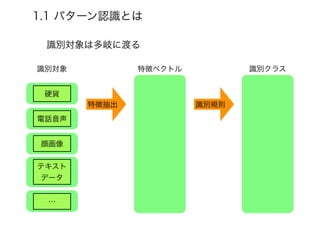
- 15. 1.1 パターン認識とは 識別対象 特徴ベクトル 識別クラス 特徴抽出 識別規則 硬貨 識別対象は多岐に渡る 電話音声 顔画像 テキスト データ …
- 16. 1.1 パターン認識とは 識別対象 特徴ベクトル 識別クラス 特徴抽出 識別規則 硬貨 特徴ベクトルの形になってしまえば, 同じ識別規則が使え る 電話音声 顔画像 テキスト データ … 特徴量1 特徴量2 特徴量3 特徴量4 … クラス1 クラス2 クラス3 … 識別不能
- 17. 1.2 特徴の型 観測された特徴
- 18. 1.2 特徴の型 観測された特徴 ? 定性的特徴(非数値データ) ? 定量的特徴(数値データ)
- 19. 1.2 特徴の型 観測された特徴 ? 定性的特徴(非数値データ) ? 名義尺度?(分類のための単なる名前)? ? 順序尺度?(順序関係を表す) ? 定量的特徴(数値データ)
- 20. 1.2 特徴の型 観測された特徴 ? 定性的特徴(非数値データ) ? 名義尺度?(分類のための単なる名前)? ? 順序尺度?(順序関係を表す) ? 定量的特徴(数値データ) ? 比例尺度?(原点が定まっており, 比率が意味を持つ) ? 間隔尺度?(一定の単位で量られた量, 量間の比が意味を持た ない)
- 21. 例題 1.1 次の特徴の型は何か. (1)試験の点数 (2)成績表のA, B, C, D (3)偏差値 (4)単語の出現頻度
- 22. 例題 1.1 次の特徴の型は何か. (1)試験の点数 → 間隔尺度 (2)成績表のA, B, C, D (3)偏差値 (4)単語の出現頻度
- 23. 例題 1.1 次の特徴の型は何か. (1)試験の点数 → 間隔尺度 (2)成績表のA, B, C, D → 順序尺度 (3)偏差値 (4)単語の出現頻度
- 24. 例題 1.1 次の特徴の型は何か. (1)試験の点数 → 間隔尺度 (2)成績表のA, B, C, D → 順序尺度 (3)偏差値 → 間隔尺度 (4)単語の出現頻度
- 25. 例題 1.1 次の特徴の型は何か. (1)試験の点数 → 間隔尺度 (2)成績表のA, B, C, D → 順序尺度 (3)偏差値 → 間隔尺度 (4)単語の出現頻度 → 比例尺度
- 28. 1.2 特徴の型 定性的な特徴を計算機上で扱うために符号化を 行う. 例1) 2クラス 男性:0, 女性:1 例2) 多クラス (5つのクラスラベルでクラス2を表現) t = (0, 1, 0, 0, 0)T
- 29. 1.3 特徴ベクトル空間と次元の呪い ? 特徴数がd個あれば, 特徴ベクトルはd次元線形 空間を張る. x1 x2 65 70 (例)?特徴数2の特徴ベクトル x = (65, 70)T
- 30. 1.3 特徴ベクトル空間と次元の呪い ? 特徴数がd個あれば, 特徴ベクトルはd次元線形 空間を張る. (例) 手書き文字認識 (kaggle)
- 31. 1.3 特徴ベクトル空間と次元の呪い ? 特徴数がd個あれば, 特徴ベクトルはd次元線形 空間を張る. (例) 手書き文字認識 (kaggle) ? 28 28=784個の画素値 ? 各画素が256階調のグレースケール
- 32. 1.3 特徴ベクトル空間と次元の呪い ? 特徴数がd個あれば, 特徴ベクトルはd次元線形 空間を張る. (例) 手書き文字認識 (kaggle) ? 28 28=784個の画素値 ? 各画素が256階調のグレースケール → 784次元のベクトル空間の各軸が256個の区 画を持っている.
- 33. 1.3 特徴ベクトル空間と次元の呪い ? 特徴数がd個あれば, 特徴ベクトルはd次元線形 空間を張る. (例) 手書き文字認識 (kaggle) ? 28 28=784個の画素値 ? 各画素が256階調のグレースケール → 784次元のベクトル空間の各軸が256個の区 画を持っている. 区画の数は全体で 256784
- 36. 例題 1.2 d次元超立方体の面(ファセットという)の数 は2d個であることを示せ. A. d次元超立方体は, 各軸の直交する二つのd-1次 元超平面で構成されるので, 面は全部で2d個あ る.
- 38. 章末問題 1.2 辺の長さが? の? 次元超立方体について, 以下 の問いに答えよ. da
- 41. 章末問題 1.2 (1)?次元超立方体の頂点の数は??個であること を示せ. ? 0次元 → 1次元 新しい軸??を 考える O x1 d 2d x1
- 42. 章末問題 1.2 (1)?次元超立方体の頂点の数は??個であること を示せ. ? 0次元 → 1次元 ??の正負の方向???の 位置に頂点を移す O1 2 a 1 2 a x1 d 2d x1 ± 1 2 a
- 43. 章末問題 1.2 (1)?次元超立方体の頂点の数は??個であること を示せ. ? 1次元の場合 O1 2 a 1 2 a x1 d 2d 頂点の数: 21 = 2
- 44. 章末問題 1.2 (1)?次元超立方体の頂点の数は??個であること を示せ. ? 1次元 → 2次元 軸??に直交する軸??を 考える O1 2 a 1 2 a x1 x2 d 2d x1 x2
- 45. 章末問題 1.2 (1)?次元超立方体の頂点の数は??個であること を示せ. ? 1次元 → 2次元 O1 2 a 1 2 a 1 2 a 1 2 a x1 x2 d 2d ??の正負の方向???の 位置に頂点を移す ± 1 2 ax2
- 46. (1)?次元超立方体の頂点の数は??個であること を示せ. ? 2次元の場合 章末問題 1.2 O1 2 a 1 2 a 1 2 a 1 2 a x1 x2 d 2d 頂点の数: 22 = 4
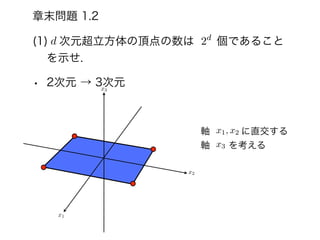
- 47. (1)?次元超立方体の頂点の数は??個であること を示せ. ? 2次元 → 3次元 章末問題 1.2 3次元空間を考える x1 x2 d 2d
- 48. (1)?次元超立方体の頂点の数は??個であること を示せ. ? 2次元 → 3次元 章末問題 1.2 x1 x2 d 2d x3 軸??? に直交する 軸??を考える x1, x2 x3
- 49. (1)?次元超立方体の頂点の数は??個であること を示せ. ? 2次元 → 3次元 章末問題 1.2 x1 x2 x3 d 2d ??の正負の方向???の 位置に頂点を移す ± 1 2 ax3
- 50. (1)?次元超立方体の頂点の数は??個であること を示せ. ? 3次元の場合 章末問題 1.2 x1 x2 x3 d 2d 頂点の数: 23 = 8
- 51. (1)?次元超立方体の頂点の数は??個であること を示せ. ? 3次元 → 4次元 章末問題 1.2 軸?????に直交する 軸??を考える x1 x2 x3 d 2d ? x1, x2, x3 x4
- 52. (1)?次元超立方体の頂点の数は??個であること を示せ. ? 3次元 → 4次元 章末問題 1.2 x1 x2 x3 d 2d ? ??の正負の方向???の 位置に頂点を移す ± 1 2 ax4
- 53. (1)?次元超立方体の頂点の数は??個であること を示せ. ? 4次元の場合 章末問題 1.2 x1 x2 x3 d 2d ? 頂点の数: 24 = 16
- 54. (1)?次元超立方体の頂点の数は??個であること を示せ. ? 同様にして, 次元が増えるごとに超立方体の頂 点の数は2倍になるので??次元超立方体の頂 点の数は??個である. 章末問題 1.2 d 2d d 2d
- 57. (2)?次元超立方体の表面積を求めよ. ? 1辺の長さが??の???次元超平面の表面積 は???と表される. 例題1.2より, これが??個あるので, 章末問題 1.2 d a d 1 ad 1 2d ad 1 ? 2d = 2dad 1
- 58. (3)超立方体を構成する??次元超平面の個数が で表されることを, 3次元立方体で確かめよ. 章末問題 1.2 m (0 ? m ? d 1) 2d m ? d m ◆
- 59. (3)超立方体を構成する超平面の個数 ? 0次元(頂点) 章末問題 1.2 23 0 ? 3 0 ◆ = 23 ? 1 = 8 x1 x2 x3
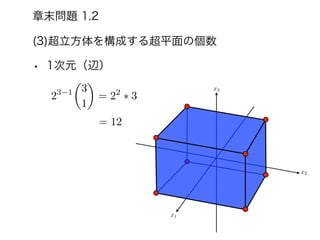
- 60. (3)超立方体を構成する超平面の個数 ? 1次元(辺) 章末問題 1.2 23 1 ? 3 1 ◆ = 22 ? 3 = 12 x1 x2 x3
- 61. (3)超立方体を構成する超平面の個数 ? 2次元(面) 章末問題 1.2 23 2 ? 3 2 ◆ = 21 ? 3 = 6 x1 x2 x3
- 64. (4)超立方体を構成する??次元超平面の総数を求 めよ. ? ??次元超平面の個数は と表されるので, それを0次元から???次元ま で合計すればよい. 章末問題 1.2 m 2d m ? d m ◆ m d 1
- 65. (4)超立方体を構成する??次元超平面の総数を求 めよ. ? ??次元超平面の個数は と表されるので, それを0次元から???次元ま で合計すればよい. よって 章末問題 1.2 m 2d m ? d m ◆ m d 1 d 1X m=0 2d m ? d m ◆
- 67. (5)その式から, 5次元超立方体を構成する超平面の 総数を求めよ. 章末問題 1.2 5 1X m=0 25 m ? 5 m ◆ = 4X m=0 25 m ? 5 m ◆
- 68. (5)その式から, 5次元超立方体を構成する超平面の 総数を求めよ. 章末問題 1.2 5 1X m=0 25 m ? 5 m ◆ = 4X m=0 25 m ? 5 m ◆ = 25 0 ? 5 0 ◆ + 25 1 ? 5 1 ◆ + 25 2 ? 5 2 ◆ + 25 3 ? 5 3 ◆ + 25 4 ? 5 4 ◆
- 69. (5)その式から, 5次元超立方体を構成する超平面の 総数を求めよ. 章末問題 1.2 5 1X m=0 25 m ? 5 m ◆ = 4X m=0 25 m ? 5 m ◆ = 25 0 ? 5 0 ◆ + 25 1 ? 5 1 ◆ + 25 2 ? 5 2 ◆ + 25 3 ? 5 3 ◆ + 25 4 ? 5 4 ◆ = 32 ? 1 + 16 ? 5 + 8 ? 10 + 4 ? 10 + 2 ? 5
- 70. (5)その式から, 5次元超立方体を構成する超平面の 総数を求めよ. 章末問題 1.2 5 1X m=0 25 m ? 5 m ◆ = 4X m=0 25 m ? 5 m ◆ = 25 0 ? 5 0 ◆ + 25 1 ? 5 1 ◆ + 25 2 ? 5 2 ◆ + 25 3 ? 5 3 ◆ + 25 4 ? 5 4 ◆ = 32 ? 1 + 16 ? 5 + 8 ? 10 + 4 ? 10 + 2 ? 5 = 32 + 80 + 80 + 40 + 10
- 71. (5)その式から, 5次元超立方体を構成する超平面の 総数を求めよ. 章末問題 1.2 5 1X m=0 25 m ? 5 m ◆ = 4X m=0 25 m ? 5 m ◆ = 25 0 ? 5 0 ◆ + 25 1 ? 5 1 ◆ + 25 2 ? 5 2 ◆ + 25 3 ? 5 3 ◆ + 25 4 ? 5 4 ◆ = 32 ? 1 + 16 ? 5 + 8 ? 10 + 4 ? 10 + 2 ? 5 = 32 + 80 + 80 + 40 + 10 = 242
- 72. ご清聴ありがとうございました。