ШҜШұШі ШӘШҰЩҲШұЫҢ ШӘШөЩ…ЫҢЩ… ЪҜЫҢШұЫҢ (1)
- 2. вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬ 1вҖ«ШӘШӘШӘШӘШӘШӘШӘвҖ¬ . вҖ«ШӘШӘШӘШӘШӘШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ 2вҖ«ШӘШӘШӘШӘШӘвҖ¬ . вҖ«ШӘвҖ¬ вҖ«ШӘШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ 3вҖ«ШӘШӘШӘШӘШӘвҖ¬ . вҖ«ШӘШӘвҖ¬ вҖ«ШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬4. вҖ«ШӘШӘШӘШӘШӘвҖ¬ вҖ«ШӘвҖ¬ 5. вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘШӘвҖ¬ 6. вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬
- 4. вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬ вҖ«ШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘШӘвҖ¬
- 6. n )xn( ... 2 )x2( 1 )x1( r1n вҖҰ r12 r11 1(A1) r2n вҖҰ r22 r21 2(A2) вҖҰ вҖҰ вҖҰ вҖҰ ... rmn вҖҰ rm2 rm1 m (Am) m
- 16. 1.1вҖ«ШөШөШөШөвҖ¬ вҖ«ШөШөШөШөШөШөШөвҖ¬ . вҖ«ШөШөШөШөвҖ¬ вҖ«ШөвҖ¬ вҖ«ШөШөШөвҖ¬ вҖ«ШөШөШөвҖ¬ пҒ¬ пҒ¬ пҒ¬ пҒ¬ пҒ¬ пҒ¬
- 17. 3.1вҖ«ШөШөШөвҖ¬ вҖ«ШөШөШөШөвҖ¬ вҖ«ШөШөШөШөШөШөШөвҖ¬ . вҖ«ШөШөШөШөвҖ¬ вҖ«ШөвҖ¬ вҖ«ШөШөШөШөвҖ¬ вҖ«ШөШөШөШөвҖ¬ вҖ«ШөШөвҖ¬ 2 пҒ¬ пҒ¬ пҒ¬ пҒ¬ пҒ¬
- 18. 2.1вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬. пҒ¬ 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10
- 19. 2вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬. 4
- 21. 1.3вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬. n )xn( ... 2 )x2( 1 )x1( r1n вҖҰ r12 r11 1(A1) r2n вҖҰ r22 r21 2(A2) вҖҰ вҖҰ вҖҰ вҖҰ ... rmn вҖҰ rm2 rm1 m (Am)
- 22. 4вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬. 10 15 1 7 4 7 3 12 2 9 5 5 20 3 5 30 3 9 1 30 4 3 1 3
- 25. вҲ‘= 4 1 2 i ija 7 1 0 4 7 15 1 0.547 0 . 3 1 5 0.560 0.547 0.367 9 3 5 5 12 2 0 . 853.40 30201215 2222 4 1 2 1 =+++ =вҲ‘=i ir 294.0 853.40 12 367.0 853.40 15 21 11 == == n n 1.5(вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬)вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬-
- 27. 6вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬. пҒ¬ пҒ¬ пҒ¬ пҒ¬ Wn вҖҰ W2 W1 xn ... x2 x1 r1n вҖҰ r12 r11 A1 r2n вҖҰ r22 r21 A2 вҖҰ вҖҰ вҖҰ вҖҰ ... rmn вҖҰ rm2 rm1 Am
- 28. 1.6вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬- ji,; 1 вҲҖ= вҲ‘= n i ij ij ij a a P )(ln 1 m k = [ ] j;ln 1 вҲҖвҲ’= вҲ‘= m i ijijj ppkE j;1 вҲҖвҲ’= jj Ed j d d w n j j j j вҲҖ= вҲ‘= ; 1
- 29. 7 10 4 7 15 1 0.292 0.227 0.308 0.292 0.195 9 3 5 5 12 2 0.375 0.068 0.384 0.208 0.156 5 30 3 9 20 3 0.208 0.682 0.231 0.375 0.260 3 1 1 3 30 4 0.125 0.023 0.077 0.125 0.389 24 44 13 24 77 Pij 77=30+20+12+15 0.195=77/15 1.6(вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬)вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬-
- 30. пҒ¬Ej 721.0 )4ln( 1 )ln( 1 === m k E1 E2 E3 E4 E5 0.956 0.947 0.913 0.625 0.947 956.0)]389.0ln(*389.0)260.0ln(*260.0 )156.0ln(*156.0)195.0ln(*195.0[721.01 =+ ++вҲ’=E dj d1 d2 d3 d4 d5 1-Ej 0.04 4 0.05 3 0.08 7 0.37 5 0.05 3 0.61 2 072.0 612.0 044.01 1 === вҲ‘ jd d wW1 W2 W3 W4 W5 0.072 0.087 0.142 0.613 0.087 1.6(вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬)вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬-
- 31. 2.6вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬- пҒ¬Aa[i,jWi/Wja[i,j пЈҙ пЈҙ пЈҙ пЈі пЈҙ пЈҙ пЈҙ пЈІ пЈұ = =+ =+ 0),( 0 0 yxg y g y f x g x f Оҙ Оҙ О» Оҙ Оҙ Оҙ Оҙ О» Оҙ Оҙ ( ) nl n j lwjwlja n i ilaiwlwila n i n j n i iwiwjwjiaL n i iWst n i n j iwjwijaz ,...,2,10 1 )( 1 )( 1 1 1 1 22),( 1 1 : 1 1 2)()min( ==+вҲ‘ = вҲ’вҲ’вҲ‘ = вҲ’ вҲ‘ = вҲ‘ = вҲ’вҲ‘ = +вҲ’= =вҲ‘ = вҲ‘ = вҲ‘ = вҲ’= О» О» ),(),( yxgyxfu О»+=
- 33. 3.6вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬вҖ«ШӘвҖ¬- nnnnnn nn nn WWaWaWa WWaWaWa WWaWaWa . . . 2211 22222121 11212111 О» О» О» =+++ =+++ =+++ пҒҢ пҒҚ пҒҢ пҒҢ WA WWA .О»=Г— n 0)det( =вҲ’ IA О» 0)( max =Г—вҲ’ WIA О» пЈҙ пЈҙ пЈі пЈҙ пЈҙ пЈІ пЈұ = пЈә пЈә пЈә пЈә пЈ» пЈ№ пЈҜ пЈҜ пЈҜ пЈҜ пЈ° пЈ® пЈә пЈә пЈә пЈә пЈ» пЈ№ пЈҜ пЈҜ пЈҜ пЈҜ пЈ° пЈ® nnnnn n n w w w aaa aaa aaa : ... :...:: ... ... 2 1 21 22221 11211
- 36. A1 3.0 5 9 24000 1 A2 1.2 7 5 25000 3 A3 1.5 9 3 32000 7 A1 1 1 1.00 0.75 1 A2 0.4 0.71 0.55 0.78 0.33 A3 0.43 0.55 0.33 1.00 0.14 Min =0.75 Min =0.33 Min =0.14 Max { min } = 0.75 A1 2Maxi min minmin max
- 37. вҖ«ШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬MaxвҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘвҖ¬ вҖ«ШӘШӘШӘШӘвҖ¬MaxвҖ«ШӘШӘвҖ¬ .вҖ«ШӘШӘШӘШӘвҖ¬ вҖ«ШӘШӘвҖ¬ вҖ«ШӘШӘШӘШӘШӘШӘвҖ¬ Max =1 пҒ¬Max =0.78 пҒ¬Max =0.14 пҒ¬Max { max } = 1 пҒ¬A1A3 A1 3.0 5 9 24000 1 A2 1.2 7 5 25000 3 A3 1.5 9 3 32000 7 A1 1 1 1.00 0.75 1 0.780.33A2 0.4 0.71 0.55 A3 0.43 0.55 0.33 1.00 0.14
- 42. 2.7-TOPSIS пҒ¬N пҒ¬W пҒ¬VnnWNV **= + jV вҲ’ jV + jd вҲ’ jd +вҲ’ вҲ’ + = ii i i dd d CL* V V m1,2,...,i,)( m1,2,...,i,)( 1 2 1 2 =вҲ’= =вҲ’= вҲ‘ вҲ‘ = вҲ’вҲ’ = ++ n j jiji n j jiji vvd vvd * iCLCL Technique for Order-Preference by Similarity to Ideal Solution
- 43. пЈә пЈә пЈә пЈ» пЈ№ пЈҜ пЈҜ пЈҜ пЈ° пЈ® = пЈә пЈә пЈә пЈә пЈ» пЈ№ пЈҜ пЈҜ пЈҜ пЈҜ пЈ° пЈ® пЈә пЈә пЈә пЈ» пЈ№ пЈҜ пЈҜ пЈҜ пЈ° пЈ® 149.0119.0063.0238.0 099.0179.0052.0119.0 198.0258.0042.0149.0 267.0000 0336.000 00092.00 000305.0 * 557.0355.0684.0781.0 371.0532.0570.0390.0 743.0769.0456.0488.0 C1 C2 C3 C4 A1 5 8 13 4 A2 4 10 9 2 A3 8 12 6 3 V .198]63,0.258,0[0.119,0.0],,,[ 4321 ==+ iiiij vMaxvMaxvMaxvMinV .099]42,0.119,0[0.238,0.0],,,[ 4321 ==вҲ’ iiiij vMinvMinvMinvMaxV 2.7-TOPSIS)вҖ«(ШӘШӘШӘШӘШӘвҖ¬
- 44. 189.0 127.0 037.0 3 2 1 = = = + + + d d d 055.0 134.0 192.0 3 2 1 = = = вҲ’ вҲ’ вҲ’ d d d 037.0)198.0198.0()258.0258.0()063.0042.0()119.0149.0( 2222 1 =вҲ’+вҲ’+вҲ’+вҲ’=+ d 225.0 513.0 838.0 * 3 * 2 * 1 = = = CL CL CL 838.0 037.0192.0 192.0* 1 = + =CL 2.7-TOPSIS)вҖ«(ШӘШӘШӘШӘШӘвҖ¬
- 45. 4.7-AHP )Analytical Hierarchy process-AHP(1980 Analytic Hierarchy Process
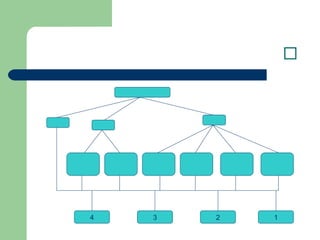
- 48. вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬ n ... 2 1 1)x1( 2)x2( ... m (xm( 1 3 5 7 9 2468
- 51. 1 3 2 2 3/1 1 4/1 4/1 2/1 4 1 2/1 2/1 4 2 1 2.33 12 5.25 3.7 5 0.43 0.25 0.38 0.5 3 0.39 8 0.14 0.08 0.05 0.0 7 0.08 5 0.21 0.33 0.19 0.1 3 0.21 8 0.21 0.33 0.38 0.2 7 0.29 9 (вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬)вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬
- 52. A B C A 1 2 8 0.59 3 B 2/1 1 6 0.34 1 C 8/1 6/1 1 0.06 6 A B C A 0.1 23 B 0.3 20 C 0.5 57 A B C A 0.08 7 B 0.27 4 A B C A 0.26 5 B 0.65 5 (вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬)вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬
- 53. 0.398 0.085 0.218 0.29 9 A 0.123 0.087 0.593 0.26 5 0.265 B 0.320 0.274 0.341 0.65 5 0.421 C 0.557 0.639 0.066 0.08 0 0.314 0.265=0.265*0.299+0.593*0.218+0.087*0.085+0.123*0.398A (вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬)вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬
- 54. вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬ An n nО»О»О» ,,, 21 пҒӢ n n i i =вҲ‘=1 О» nвүҘmaxО» maxО»
- 55. nn (вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬)вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬ 1 .. max вҲ’ вҲ’ = n n II О» ... .. .. RII II RI = n 1 2 3 4 5 6 7 8 9 10 I.I.R. 0 0 0.58 0.9 1.12 1.24 1.32 1.41 1.45 1.45 maxО» maxО»



























![1.6вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬-
ji,;
1
вҲҖ=
вҲ‘=
n
i
ij
ij
ij
a
a
P
)(ln
1
m
k =
[ ] j;ln
1
вҲҖвҲ’= вҲ‘=
m
i
ijijj ppkE j;1 вҲҖвҲ’= jj Ed
j
d
d
w n
j
j
j
j вҲҖ=
вҲ‘=
;
1](https://image.slidesharecdn.com/p-180313121144/85/1-28-320.jpg)

![пҒ¬Ej
721.0
)4ln(
1
)ln(
1
===
m
k
E1 E2 E3 E4 E5
0.956 0.947 0.913 0.625 0.947
956.0)]389.0ln(*389.0)260.0ln(*260.0
)156.0ln(*156.0)195.0ln(*195.0[721.01
=+
++вҲ’=E
dj d1 d2 d3 d4 d5
1-Ej
0.04
4
0.05
3
0.08
7
0.37
5
0.05
3
0.61
2
072.0
612.0
044.01
1 ===
вҲ‘ jd
d
wW1 W2 W3 W4 W5
0.072 0.087 0.142 0.613 0.087
1.6(вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬)вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬вҖ«ШөвҖ¬-](https://image.slidesharecdn.com/p-180313121144/85/1-30-320.jpg)












![пЈә
пЈә
пЈә
пЈ»
пЈ№
пЈҜ
пЈҜ
пЈҜ
пЈ°
пЈ®
=
пЈә
пЈә
пЈә
пЈә
пЈ»
пЈ№
пЈҜ
пЈҜ
пЈҜ
пЈҜ
пЈ°
пЈ®
пЈә
пЈә
пЈә
пЈ»
пЈ№
пЈҜ
пЈҜ
пЈҜ
пЈ°
пЈ®
149.0119.0063.0238.0
099.0179.0052.0119.0
198.0258.0042.0149.0
267.0000
0336.000
00092.00
000305.0
*
557.0355.0684.0781.0
371.0532.0570.0390.0
743.0769.0456.0488.0
C1 C2 C3 C4
A1 5 8 13 4
A2 4 10 9 2
A3 8 12 6 3
V
.198]63,0.258,0[0.119,0.0],,,[ 4321 ==+
iiiij vMaxvMaxvMaxvMinV
.099]42,0.119,0[0.238,0.0],,,[ 4321 ==вҲ’
iiiij vMinvMinvMinvMaxV
2.7-TOPSIS)вҖ«(ШӘШӘШӘШӘШӘвҖ¬](https://image.slidesharecdn.com/p-180313121144/85/1-43-320.jpg)




![вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬вҖ«ЩҠвҖ¬
пҒ¬
ABBCAC
пҒ¬a[i,k].a[k,j]=a[i,jijk
пҒ¬1.0](https://image.slidesharecdn.com/p-180313121144/85/1-49-320.jpg)









