1. kuliah pertama or reguler 2015
- 1. RISET OPERASI (OPERATIONS RESEARCH / OPERATIONAL RESEARCH) Windu Partono 2015
- 3. Riset Operasi (Operational Research) merupakan satu cabang ilmu yang berasal dari Inggris dan dikembangkan dari hasil studi operasi-operasi militer selama Perang Dunia II. Setelah perang selesai, potensi komersial dari cabang ilmu ini berkembang dengan pesat di Amerika Serikat dan lebih dikenal dengan nama Operations Research
- 4. Istilah Operational Research pertama kali diperkenalkan pada tahun 1940 oleh Mc Closky dan Trefthen di suatu kota kecil, Bowdsey, Inggris. Pada masa awal perang tahun 1939, pemimpin militer Inggris memanggil sekelompok ahli sipil dari berbagai disiplin ilmu dan mengkoordinasikan mereka kedalam satu kelompok yang mendapat tugas mencari cara-cara efisien untuk menempatkan radar dalam suatu sistem peringatan dini untuk menghadapi serangan udara.
- 5. Keberhasilan kelompok peneliti operasi- operasi militer ini menarik perhatian para industriawan dan kemudian mereka diminta untuk membantu menyelesaikan masalah- masalah yang rumit terutama menyangkut persoalan : pengalokasian sumber daya yang sangat terbatas untuk menghasilkan suatu produk secara efisien.
- 6. Awal tahun 1950 merupakan awal dasawarsa dimana teknik-teknik yang dikembangkan dalam Riset Operasi meluas di kedua negara Inggris dan Amerika Serikat terutama setelah ditemukannya teknik pemrograman linear, pemrograman non linear, pemrograman dinamik dan teknik antrian pada masalah-masalah produksi dan distribusi. Di Indonesia Riset Operasi mulai berkembang dengan cepat pada awal tahun 1974.
- 7. Pengertian dasar tentang Riset Operasi
- 8. Riset Operasi (OR) merupakan metode-metode ilmiah untuk memecahkan masalah pengalokasian sumber daya (manusia, mesin, bahan dan uang) pada suatu sistem industri, bisnis, pemerintahan dan pertahanan. Tujuan OR membentuk suatu model ilmiah dengan menggabungkan faktor kesempatan dan resiko untuk meramalkan suatu keputusan atau strategi.
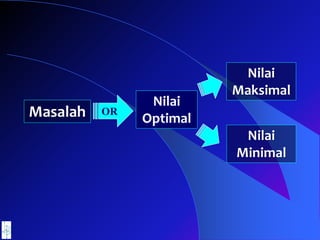
- 10. Salah satu tujuan yang sering diharapkan dari Riset Operasi adalah untuk mencari : nilai maksimal (profit, performa, hasil, dll) atau nilai minimal (kerugian, risiko, biaya, dll) pada pengolahan sumber daya.
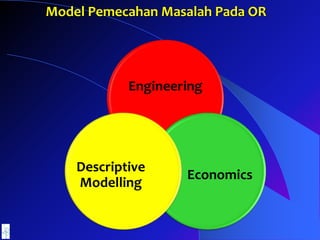
- 11. Model Pemecahan Masalah Pada OR Engineering Economics Descriptive Modelling
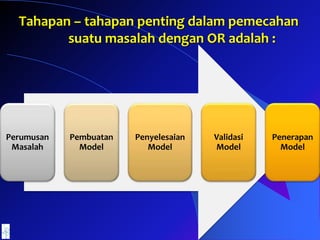
- 12. Tahapan tahapan penting dalam pemecahan suatu masalah dengan OR adalah : Perumusan Masalah Pembuatan Model Penyelesaian Model Validasi Model Penerapan Model
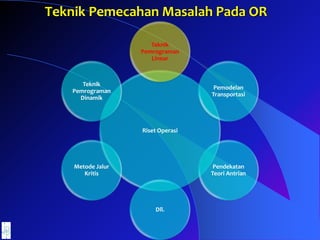
- 13. Riset Operasi Teknik Pemrograman Linear Pemodelan Transportasi Pendekatan Teori Antrian Dll. Metode Jalur Kritis Teknik Pemrograman Dinamik Teknik Pemecahan Masalah Pada OR
- 15. Pemrograman linear (garis lurus) merupakan suatu model umum yang dapat digunakan dalam masalah pengalokasian sumber sumber yang terbatas secara optimal Masalah akan muncul jika seseorang diharuskan memilih atau menentukan setiap kegiatan yang akan dilaksanakannya dimana setiap kegiatan membutuhkan sumber daya yang sama sedangkan jumlah sumber daya terbatas
- 16. Contoh aplikasi teknik pemrograman linear Perusahaan / Developer yang bergerak pada pembangunan rumah tinggal sering berhadapan dengan persoalan penentuan jumlah rumah dan tipe rumah yang paling menguntungkan. Persoalan cash flow pada sebuah perusahaan konstruksi jika akan menangani beberapa proyek secara bersamaan dengan kondisi keuangan yang sangat terbatas. Penentuan jumlah kendaraan umum yang harus beroperasi pada satu trayek. Bagian produksi suatu perusahaan dihadapkan pada masalah penentuan tingkat produksi masing-masing jenis barang dengan memperhatikan faktor-faktor produksi seperti mesin, tenaga kerja, bahan mentah dan lain sebagainya.
- 17. Contoh kasus 1. Sebuah perusahaan pengembang akan membangun 80 unit rumah dengan 2 (dua) tipe yang berbeda yaitu Tipe 45 dengan luas tanah 120 m2 Tipe 60 dengan luas tanah 200 m2 Luas total areal tanah adalah 20000 m2 dengan pola bangun 60% perumahan dan 40% untuk fasilitas umum, jalan, taman dll. Dari hasil perkiraan nilai jual dan keuntungan yang diperoleh jika membayar secara kontan, maka rumah tipe 45 akan mendapat keuntungan bersih Rp. 10 juta sedangkan Tipe 60 akan mendapatkan keuntungan Rp. 15 juta per unit. Dari data-data tersebut diminta menghitung jumlah rumah untuk masing-masing tipe dengan keuntungan bersih yang terbesar
- 18. Jika banyaknya rumah tipe 45 yang akan dibangun sebanyak X1 unit dan tipe 60 sebanyak X2 unit, Keuntungan maksimal yang direncanakan akan diperoleh sebesar 10 X1 + 15 X2 (juta rupiah). Jumlah rumah maksimum sebanyak 80 buah, maka X1 + X2 80 Luas areal rumah = 60% atau sebesar 12000 m2. Luas total areal rumah adalah sebesar 120 X1 + 200 X2 yang nilainya tidak melebihi 12000 m2. Atau 12 X1 + 20 X2 1200 Tahap 1 : Merumuskan Masalah
- 19. Secara matematis persoalan tersebut dapat dimodelkan sbb.: Fungsi Tujuan : Maksimum Z = 10 X1 + 15 X2 Fungsi Batasan : X1 + X2 80 12 X1 + 20 X2 1200 X1 0; X2 0 Tahap 2 : Pembuatan Model
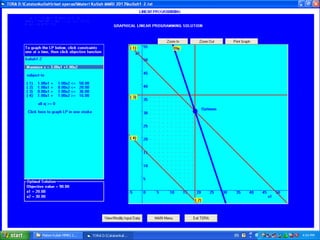
- 20. Untuk menyelesaikan persoalan tersebut di atas dapat dilakukan dengan menggunakan Cara ANALITIS Cara GRAFIS Untuk menyelesaikan persoalan tersebut pertama-tama akan menggunakan cara grafis. Tahap 3 : Penyelesaian Model
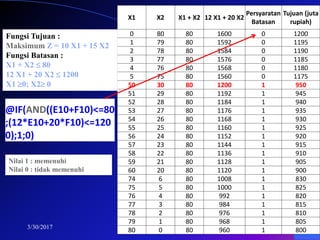
- 21. 3/30/2017 21 X1 X2 X1 + X2 12 X1 + 20 X2 Persyaratan Batasan Tujuan (juta rupiah) 0 80 80 1600 0 1200 1 79 80 1592 0 1195 2 78 80 1584 0 1190 3 77 80 1576 0 1185 4 76 80 1568 0 1180 5 75 80 1560 0 1175 50 30 80 1200 1 950 51 29 80 1192 1 945 52 28 80 1184 1 940 53 27 80 1176 1 935 54 26 80 1168 1 930 55 25 80 1160 1 925 56 24 80 1152 1 920 57 23 80 1144 1 915 58 22 80 1136 1 910 59 21 80 1128 1 905 60 20 80 1120 1 900 74 6 80 1008 1 830 75 5 80 1000 1 825 76 4 80 992 1 820 77 3 80 984 1 815 78 2 80 976 1 810 79 1 80 968 1 805 80 0 80 960 1 800 @IF(AND((E10+F10)<=80 ;(12*E10+20*F10)<=120 0);1;0) Fungsi Tujuan : Maksimum Z = 10 X1 + 15 X2 Fungsi Batasan : X1 + X2 80 12 X1 + 20 X2 1200 X1 0; X2 0 Nilai 1 : memenuhi Nilai 0 : tidak memenuhi
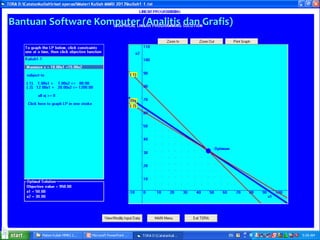
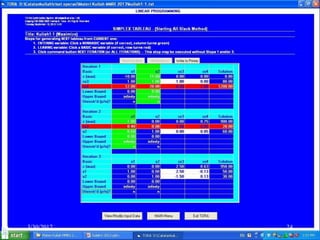
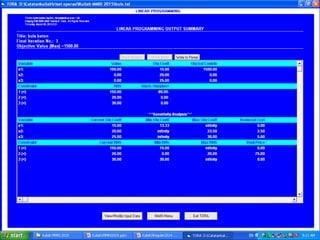
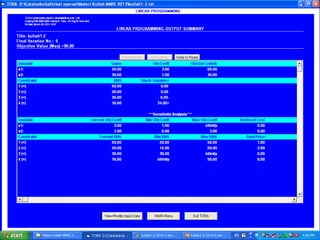
- 23. 3/30/2017 23 Bantuan Software Komputer (Analitis dan Grafis)
- 24. 3/30/2017 24
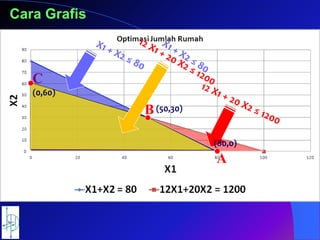
- 25. Karena dua garis berpotongan pada satu titik, maka harus ditentukan koordinat titik potong tersebut. X1 + X2 = 80 (1) 12 X1 + 20 X2 = 1200 (2) Substitusi persamaan (1) ke persamaan (2) 12 (80 X2) + 20 X2 = 1200 960 12 X2 + 20 X2 = 1200 8 X2 = 240 X2 = 30 Dari persamaan(1) akan diperoleh X1 = 50
- 26. Dari gambar kedua fungsi dan batasan-batasan yang ada maka daerah yang memenuhi kedua fungsi batasan adalah daerah yang di arsir hijau. Untuk menentukan pasangan X1 dan X2 yang memenuhi syarat, maka dapat diambil sebarang harga X1 dan X2 dengan ketentuan pasangan X1, X2 harus terletak di daerah hijau. Untuk memudahkan penyelesaian masalah maka diambil pasangan koordinat : A : (80,0) B : (50,30) C : (0,60)
- 27. Dari hasil perhitungan nilai Z untuk setiap pasangan X1 dan X2 maka akan diperoleh : Dari hasil perhitungan tersebut, maka pasangan X1 = 50 dan X2 = 30 akan memberikan nilai Z yang terbesar yaitu 950. X1 X2 Z 0 60 900 50 30 950 80 0 800
- 28. Pada perhitungan di atas hanya diambil tiga titik A, B dan C. Pertanyaan yang muncul adalah apakah pada daerah hijau ada titik lain yang akan memberikan pasangan X1 dan X2 sehingga nilai Z mencapai maksimum atau lebih besar dari 950: Jumlah titik yang bisa diambil pada daerah hijau sangat banyak dan bahkan tak terhingga sehingga sulit bagi kita untuk menguji satu persatu. Cara yang paling mudah adalah dengan cara coba-coba dan tentunya cara ini juga akan memakan waktu yang lama. Tahap 4 : Validasi Model
- 29. Sebagai contoh jika kita ambil beberapa titik yang ada disisi kanan dari daerah hijau Tahap 4 : Validasi Model 70 10 850 60 20 900 40 36 940
- 30. Dari hasil tersebut, maka tipe rumah yang akan dibangun adalah 50 unit Tipe 45 dan 30 unit tipe 60 dengan perkiraan keuntungan maksimum Rp. 950 juta. Tahap 5 : Penerapan Model
- 31. 3/30/2017 Sebuah perusahaan pembuat beton pracetak mempunyai usaha pada pembuatan pipa beton (buis beton) dengan tiga jenis diameter yaitu 60cm, 80 cm dan 100 cm. Material utama pembuatan ketiga jenis beton pracetak tersebut adalah semen, pasir dan split 1 cm. Contoh kasus 2.
- 32. 3/30/2017 Untuk pembuatan ketiga jenis pipa beton tersebut, memerlukan jumlah material dan waktu pelaksanaan sebagai berikut : Tipe Buis Beton Semen (zak) Pasir (m3) Split (m3) 60 cm 0.7 0.2 0.3 80 cm 1 0.3 0.45 100 cm 1.5 0.4 0.6
- 33. 3/30/2017 Keuntungan yang diperoleh untuk setiap penjualan buis beton tipe 60, 80 dan 100 masing-masing adalah Rp 150000,-, Rp 200000,- dan Rp 250000,-. Saat ini di pabrik hanya tersedia 150 zak semen, 20 m3 pasir dan 30 m3 split. Dari jumlah material yang ada, berapa jumlah buis beton yang dapat diproduksi oleh perusahaan agar keuntungan maksimum dengan asumsi tidak ada penambahan material
- 34. 3/30/2017 Jawab : Diasumsikan jumlah buis beton tipe 60, 80 dan 100 masing-masing sebanyak X1, X2 dan X3
- 35. 3/30/2017 Jawab : Jumlah semen yang diperlukan adalah : 0.7X1 + X2 + 1.5 X3 Jumlah semen yang tersedia : 150 zak Maka dapat dirumuskan : 0.7 X1 + X2 + 1.5 X3 150
- 36. 3/30/2017 Jawab : Jumlah pasir yang diperlukan adalah : 0.2X1 + 0.3X2 + 0.4 X3 Jumlah pasir yang tersedia : 20 m3 Maka dapat dirumuskan : 0.2 X1 + 0.3X2 + 0.4 X3 20
- 37. 3/30/2017 Jawab : Jumlah split yang diperlukan adalah : 0.3X1 + 0.45X2 + 0.6 X3 Jumlah split yang tersedia : 30 m3 Maka dapat dirumuskan : 0.3 X1 + 0.45X2 + 0.6 X3 30
- 38. 3/30/2017 Keuntungan yang diperoleh adalah : 15X1 + 20X2 + 25 X3 Tujuan persoalan ini adalah mendapatkan keuntungan sebesar mungkin, maka fungsi tujuan adalah : Maksimum Z = 15X1 + 20X2 + 25 X3
- 39. 3/30/2017 Model metematis adalah sbb.: Fungsi Tujuan : Maksimum Z = 15X1 + 20X2 + 25 X3 Fungsi Batasan : 0.7 X1 + X2 + 1.5 X3 150 0.2 X1 + 0.3X2 + 0.4 X3 20 0.3 X1 + 0.45X2 + 0.6 X3 30 X1,X2, X3 0;
- 40. 3/30/2017 Jawab: X1 = 100 X2 = 0 X3 = 0 Keuntungan : Rp. 15,000,000.00
- 41. 3/30/2017
- 42. 3/30/2017 Melihat hasil analisis tersebut terlihat perusahaan hanya membuat buis beton dengan tipe 1 ( 60 cm). Perusahaan berkeinginan membuat alternatif produksi dengan membatasi setiap tipe buis beton maksimum 50. Bagaimana jawaban persoalan ini dan berapa keuntungan maksimum yang akan diperoleh perusahaan.
- 43. 3/30/2017 Keuntungan yang diperoleh untuk setiap penjualan buis beton tipe 60, 80 dan 100 masing-masing adalah Rp 150000,-, Rp 200000,- dan Rp 250000,-. Saat ini di pabrik hanya tersedia 150 zak semen, 20 m3 pasir dan 30 m3 split. Dari jumlah material yang ada, berapa jumlah buis beton yang dapat diproduksi oleh perusahaan agar keuntungan maksimum dengan asumsi tidak ada penambahan material
- 44. 3/30/2017 Jawab: X1 = 50 X2 = 33.33 X3 = 0 Keuntungan : Rp. 14,166,700.00
- 45. 3/30/2017 Jawab alternatif: X1 = 50 X2 = 33 X3 = 0 Keuntungan : 50x15 + 33 x 20 = Rp. 14,100,000.00
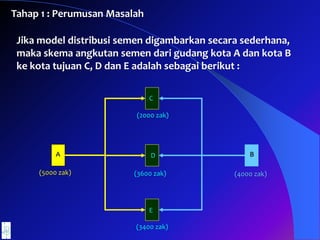
- 46. Contoh 3. Sebuah distributror semen mempunyai cadangan 9000 zak semen yang disimpan di dua gudang. Gudang pertama terletak di kota A sedangkan gudang kedua terletak di kota B. Jumlah semen yang ada di dua gudang tersebut masing-masing 5000 zak semen ada di gudang pertama dan 4000 zak semen ada di gudang kedua. Pada saat yang bersamaan datang pesanan dari kota C, D dan E. Pesanan dari kota C sebanyak 2000 zak Pesanan dari kota D sebanyak 3600 zak Pesanan dari kota E sebanyak 3400 zak Untuk memenuhi permintaan dari tiga kota tersebut diatas, distributor tersebut akan menggunakan truk sebagai alat angkut semen dengan daya angkut setiap truk maksimum100 zak semen Biaya pengangkutan dari kedua gudang menuju ke 3 kota pemesan ditunjukkan dengan tabel berikut :
- 47. Tabel biaya pengangkutan (rupiah) Kota C Kota D Kota E Gudang Kota A 420000 550000 600000 Gudang Kota B 360000 470000 510000 Distributor tersebut harus menentukan atau memutuskan bagaimana mendistribusikan ke 9000 zak semen tersebut sehingga biaya pengeluarannya se minimum mungkin
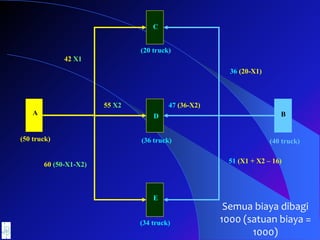
- 48. Tahap 1 : Perumusan Masalah Jika model distribusi semen digambarkan secara sederhana, maka skema angkutan semen dari gudang kota A dan kota B ke kota tujuan C, D dan E adalah sebagai berikut : A B (5000 zak) (4000 zak) C D E (2000 zak) (3600 zak) (3400 zak)
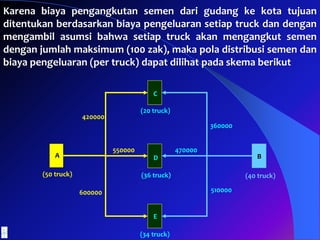
- 49. A B 420000 360000 600000 510000 550000 470000 (50 truck) (40 truck) C D E (20 truck) (36 truck) (34 truck) Karena biaya pengangkutan semen dari gudang ke kota tujuan ditentukan berdasarkan biaya pengeluaran setiap truck dan dengan mengambil asumsi bahwa setiap truck akan mengangkut semen dengan jumlah maksimum (100 zak), maka pola distribusi semen dan biaya pengeluaran (per truck) dapat dilihat pada skema berikut
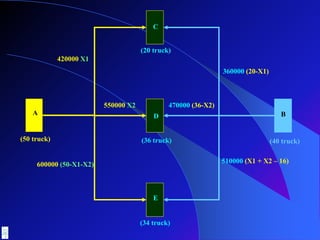
- 50. Untuk menjawab persoalan tersebut, kita misalkan jumlah semen yang dikirim dari A ke C sebanyak X1 truck dan dari A ke D sebanyak X2 truck maka jumlah semen yang dikirim dari A ke E sebanyak (50 X1 - X2) Karena kota C sudah menerima sebanyak X1 dari kota A, maka sisa permintaan sebanyak (20 X1) dikirim dari kota B Karena kota D sudah menerima sebanyak X2 dari kota A, maka sisa permintaan sebanyak (36 X2) dikirim dari kota B Karena kota E sudah menerima sebanyak (50-X1-X2) dari kota A, maka sisa permintaan sebanyak (34 (50-X1-X2) ) dikirim dari kota B atau sebanyak (X1 + X2 16)
- 51. Secara tabelaris, distribusi pengiriman terlihat sebagai berikut : Kota C (20 truck) Kota D (36 truck) Kota E (34 truck) Gudang Kota A (50 truck) X1 X2 (50-X1-X2) Gudang Kota B (40 truck) (20 X1) (36 X2) ( X1 + X2 16) Dari asumsi distribusi semen seperti terlihat pada tabel di atas, maka skema pembiayaan untuk pengiriman seluruh semen adalah sebagai berikut
- 52. A B 420000 X1 360000 (20-X1) 600000 (50-X1-X2) 510000 (X1 + X2 16) 550000 X2 470000 (36-X2) (50 truck) (40 truck) C D E (20 truck) (36 truck) (34 truck)
- 53. A B 42 X1 36 (20-X1) 60 (50-X1-X2) 51 (X1 + X2 16) 55 X2 47 (36-X2) (50 truck) (40 truck) C D E (20 truck) (36 truck) (34 truck) Semua biaya dibagi 1000 (satuan biaya = 1000)
- 54. Dari skema penegluaran biya angkutan tersebut, maka Biaya total (dalam ribuan) yang dikeluarkan untuk mengirimkan 9000 zak semen adalah sebagai berikut : Total biaya = 42 X1 + 55 X2 + 60 (50 X1 X2) + 36 (20 X1) + 47 (36 X2) + 51 (X1 + X2 16) Total biaya = 42 X1 + 55 X2 + 3000 60X1 60X2 + 720 36X1 + 1692 47X2 + 51X1 + 51X2 816 Total biaya = 4596 3 X1 X2 Dari uraian di atas maka perusahaan akan untung jika pengeluarannya seminimum mungkin. Pengeluaran seminimal mungkin adalah tujuan yang dikehendaki pada persoalan ini. Minimum Z = 4596 3 X1 X2
- 55. Secara matematis tujuan yang hendak dicapai dapat dinyatakan dengan Minimum Z = 4596 3 X1 X2 Dari rumus matematis di atas, maka harga X1 dan X2 harus diambil sedemikian rupa sehingga nilai Z yang diperloh adalah yang paling terkecil (minimum). Karena harga 4596 adalah suatu harga yang konstan, maka harga Z akan minimum jika harga (3X1 + X2) sebesar mungkin. Maka persamaan di atas dapat diubah menjadi Maksimum ZB = 3 X1 + X2
- 56. Dari pola distribusi semen, maka berapapun nilai X1 dan X2 yang diperoleh maka persyaratan lain yang harus dipenuhi untuk menyelesaikan persoalan ini adalah tidak boleh mengirim semen dengan jumlah negatif. Alasan ini logis karena tidak mungkin kita mengirim barang dengan jumlah negatif Kota C (20 truck) Kota D (36 truck) Kota E (34 truck) Gudang Kota A (50 truck) X1 X2 (50-X1-X2) Gudang Kota B (40 truck) (20 X1) (36 X2) ( X1 + X2 16) Harus bernilai positif
- 57. Dari uraian di atas, maka persyaratan yang harus dipenuhi pada persoalan ini dapat dinyatakan dengan ketidak-samaan sebagai berikut : X1 0; X2 0 50 - X1 X2 0 20 - X1 0 36 X2 0 X1 + X2 16 0 Ketidak samaan di atas dapat disederhanakan menjadi : X1 + X2 50 X1 20 X2 36 X1 + X2 16 X1 0 X2 0
- 58. Model matematis dari persoalan di atas dapat dinyatakan sebagai berikut Fungsi Tujuan : Maksimum ZB = 3 X1 + X2 Fungsi Batasan : X1 + X2 50 X1 20 X2 36 X1 + X2 16 X1 0; X2 0 Tahap 2 : Pembentukan Model
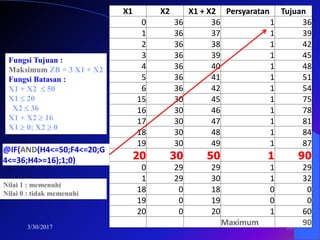
- 59. 3/30/2017 59 Fungsi Tujuan : Maksimum ZB = 3 X1 + X2 Fungsi Batasan : X1 + X2 50 X1 20 X2 36 X1 + X2 16 X1 0; X2 0 X1 X2 X1 + X2 Persyaratan Tujuan 0 36 36 1 36 1 36 37 1 39 2 36 38 1 42 3 36 39 1 45 4 36 40 1 48 5 36 41 1 51 6 36 42 1 54 15 30 45 1 75 16 30 46 1 78 17 30 47 1 81 18 30 48 1 84 19 30 49 1 87 20 30 50 1 90 0 29 29 1 29 1 29 30 1 32 18 0 18 0 0 19 0 19 0 0 20 0 20 1 60 Maximum 90 @IF(AND(H4<=50;F4<=20;G 4<=36;H4>=16);1;0) Nilai 1 : memenuhi Nilai 0 : tidak memenuhi
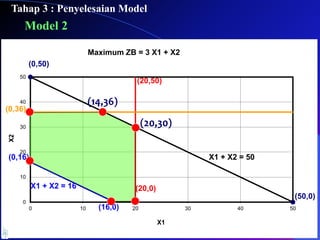
- 60. Model 2 (0,50) (50,0) (20,0) (20,50) (16,0) (0,16) (0,36) X1 + X2 = 50 X1 + X2 = 16 0 10 20 30 40 50 0 10 20 30 40 50 X2 X1 Maximum ZB = 3 X1 + X2 Tahap 3 : Penyelesaian Model (14,36) (20,30)
- 64. Dari hasil perhitungan nilai ZB untuk setiap pasangan X1 dan X2 maka akan diperoleh : Dari hasil perhitungan tersebut, maka pasangan X1 = 20 dan X2 = 30 akan memberikan nilai ZB yang terbesar yaitu 90. X1 X2 ZB 0 16 16 16 0 48 20 0 60 20 30 90 14 36 78 0 36 36
- 65. Secara tabelaris, distribusi pengiriman semen dapat dilihat pada tabel di bawah ini : Kota C (20 truck) Kota D (36 truck) Kota E (34 truck) Gudang Kota A (50 truck) 20 30 0 Gudang Kota B (40 truck) 0 6 34 Dengan pola distribusi tersebut, maka nilai ZB maksimum adalah 90 (ribu rupiah)
- 66. Untuk validasi model dapat dilakukan dengan cara yang sama seperti contoh pertama Tahap 4 : Validasi Model Tahap 5 : Penerapan Model Dengan nilai ZB maksimum = 90, maka nilai Z minimum : Z = 4596 ZB Z = 4596 90 = 4506 atau Z = 4596 3 X1 X2 Z = 4596 3 * 20 30 = 4506 Atau biaya pengeluaran maksimum yang akan dikeluarkan oleh perusahaan tersebut diperkirakan sebesar Rp. 45060000.00,-
- 67. Bagaimana jika kita mempunyai model metematis dalam bentuk sbb: Maksimum Z = 50000 X1 + 60000 X2 + 40000 X3 Fungsi Batasan : 0.2 X1 + 0.2 X2 + 0.3 X3 60 2 X1 + 3 X2 + 3 X3 3200 42 X1 + 5 X2 + 6 X3 6000 6 X1 + 7.5 X2 + 10.5 X3 8000 X1 0; X2 0; X3 0 Apakah model ini dapat diselesaikan secara grafis atau menggunakan Microsoft Excel ?
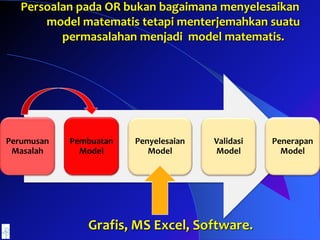
- 68. Persoalan pada OR bukan bagaimana menyelesaikan model matematis tetapi menterjemahkan suatu permasalahan menjadi model matematis. Perumusan Masalah Pembuatan Model Penyelesaian Model Validasi Model Penerapan Model Grafis, MS Excel, Software.
- 69. Daftar Pustaka 1. Hamdy A, Taha : Operations Research, alih bahasa Riset Operasi Suatu Pengantar, Daniel Wirajaya, Binarupa Aksara, Jakarta, 1996. 2. Sri Mulyono :Operations Research, Lembaga Penerbit Fakultas Ekonomi Universitas Indonesia, Jakarta, 1999. 3. Siswanto :Pemrograman Linear Lanjutan, Penerbit Universitas Atma Jaya Yogyakarta, Yogyakarta, 1992.
- 71. Mulai kuliah ke 2 mahasiswa diwajibkan membawa komputer. Software TORA harus di install pada masing-masing komputer. Sebaiknya menggunakan komputer 32 bits. Catatan :