1 L├Łmits i continu├»tat de funcions
- 1. Temari matem├Ātiques 2n de Batxillerat 1. L├Łmits i continu├»tat de funcions (7) 2. Derivades (8) 3. Aplicacions de la derivada (9-10) 4. Primitives, integrals indefinides (11) 5. Integrals definides (12) 6. Matrius i determinants (1-2) 7. Sistemes d'equacions lineals (3) 8. Geometria a l'espai (4) 9. Dist├Āncies i angles (5-6) AN├ĆLISI ├ĆLGEBRA LINEAL GEOMETRIA 1T 2T 3T 3 grans temes de la sele:
- 2. Tema 1(7): L├Łmits i continu├»tat de funcions 1. Concepte de l├Łmit 2. C├Ālcul de l├Łmits 3. Indeterminacions 4. L├Łmits en funcions 5. Rep├Ās funcions principals 6. Teoremes a l'entorn dels l├Łmits
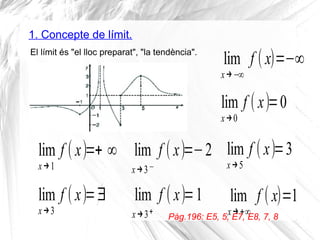
- 3. 1. Concepte de l├Łmit. El l├Łmit ├®s "el lloc preparat", "la tend├©ncia". lim xŌåÆ1 f ( x)=+ Ōł× lim xŌåÆ3 f ( x)=Ōłā lim xŌåÆ3ŌłÆ f ( x)=ŌłÆ2 lim xŌåÆ3+ f ( x)=1 lim xŌåÆ5 f ( x)=3 lim xŌåÆ+Ōł× f ( x)=1 lim xŌåÆ0 f ( x)=0 lim xŌåÆŌłÆŌł× f ( x)=ŌłÆŌł× P├Āg.196: E5, 5, E7, E8, 7, 8
- 4. 2. C├Ālcul de l├Łmits. a) L├Łmits de pot├©ncies: lim xŌåÆ+Ōł× xn = Exemples de cada un, P├Āg.200: 13,14 +Ōł× si n > 0 1 si n = 0 0 si n < 0 lim xŌåÆŌłÆŌł× xn = +Ōł× si n > 0 i parell -Ōł× si n > 0 i senar 1 si n = 0 0 si n < 0 lim xŌåÆ+Ōł× ax = +Ōł× si a > 1 0 si 0<a<1 ├ś si a < 0 lim xŌåÆŌłÆŌł× ax = 0 si a > 1 +Ōł× si 0<a<1 0 si a < 0 variablealabasevariableal'exponent
- 5. 2. C├Ālcul de l├Łmits. b) L├Łmits de polinomis: lim xŌåÆ┬▒Ōł× (ak xk + akŌłÆ1 xkŌłÆ1 +...+ a1 x+a0 )= = lim xŌåÆ┬▒Ōł× ak xk =ak ┬Ę lim xŌåÆ┬▒Ōł× xk =a k ┬Ę(┬▒Ōł×) Atenci├│ amb els signes! c) L├Łmits de quocients entre polinomis: lim xŌåÆ┬▒Ōł×(ak x k bp xp)= ak b p ┬Ę lim xŌåÆ┬▒Ōł×(x k xp)= Menyspreant termes de grau inferior: ┬▒Ōł× si k > p 0 si p > k ak/bp si p = k p201: E12, 15, 16
- 6. 2. C├Ālcul de l├Łmits. d) Propietats de les operacions amb l├Łmits: lim xŌåÆ+Ōł× [ f ( x)┬▒g( x)]= lim xŌåÆ+ Ōł× f ( x)┬▒ lim xŌåÆ+Ōł× g( x) lim xŌåÆ+Ōł× [ f ( x)┬Ę g( x)]=lim xŌåÆ+Ōł× f ( x)┬Ę lim xŌåÆ+ Ōł× g( x) lim xŌåÆ+Ōł× f (x) g (x) = lim xŌåÆ+ Ōł× f ( x) lim xŌåÆ+ Ōł× g( x) (si lim g(x) diferent de 0)
- 7. lim xŌåÆ+Ōł× p ŌłÜ f (x)=p ŌłÜ lim xŌåÆ+ Ōł× f ( x) lim xŌåÆ+Ōł× [ f ( x)]p =[ lim xŌåÆ+Ōł× f ( x)]p lim xŌåÆ+Ōł× loga f ( x)=loga lim xŌåÆ+Ōł× f ( x) lim xŌåÆ+Ōł× f ( x)g( x) =( lim xŌåÆ+Ōł× f ( x))lim xŌåÆ+Ōł× g(x) (si lim f(x) i lim g(x) diferent de 0) p199: E9, 11, 12, 44 i 45 cap de setmana
- 8. 3. Indeterminacions a) Ōł×/Ōł× b) Ōł× - Ōł× c) 1Ōł× lim xŌåÆ+Ōł× 3x2 ŌłÜ 4x+1 = Ōł× Ōł× Dividir numerador i denominador entre la pot├©ncia m├®s gran de x Resoldre la resta de fraccions Multiplicat pel conjugat (entre arrels) Novetat! a) Ōł×/Ōł× grau 2 grau 1/2
- 9. 3. Indeterminacions lim xŌåÆ+Ōł× 3x2 ŌłÜ 4x+1 = Ōł× Ōł× a) Ōł×/Ōł× grau 2 grau 1/2 lim xŌåÆ+Ōł× 3x2 x 2 ŌłÜ 4x+1 x 2 = lim xŌåÆ+Ōł× 3 ŌłÜ4x x4 + 1 x4 = 3 0 =+Ōł× Altre exemple p202, 17, 18
- 10. 3. Indeterminacions lim xŌåÆ+Ōł×(x 2 ŌłÆ3 xŌłÆ5 ŌłÆ x 3 x2 + 1)=Ōł×ŌłÆŌł× b1) Ōł× - Ōł× (resta) x2 ŌłÆ3 xŌłÆ5 ŌłÆ x3 x 2 +1 = (x2 ŌłÆ3)( x2 + 1)ŌłÆx3 ( xŌłÆ5) (xŌłÆ5)(x 2 +1) = x4 + x2 ŌłÆ3x2 ŌłÆ3ŌłÆx4 + 5x3 x 3 + xŌłÆ5x 2 ŌłÆ5 = 5x3 ŌłÆ2x2 ŌłÆ3 x 3 ŌłÆ5x 2 +xŌłÆ5 lim xŌåÆ+Ōł×(5x 3 x3 )=5
- 11. 3. Indeterminacions lim xŌåÆŌłÆŌł× (ŌłÜ x4 +1ŌłÆŌłÜx2 ŌłÆ1)=Ōł×ŌłÆŌł× b2) Ōł× - Ōł× (conjugat) (ŌłÜ x4 + 1ŌłÆŌłÜ x2 ŌłÆ1 )┬Ę(ŌłÜ x4 + 1+ ŌłÜx2 ŌłÆ1) ŌłÜ x4 + 1+ŌłÜ x2 ŌłÆ1 = x 4 + 1ŌłÆ( x 2 ŌłÆ1) ŌłÜ x4 +1+ ŌłÜx2 ŌłÆ1 lim xŌåÆŌłÆŌł× x4 ŌłÆx2 +2 ŌłÜ x4 + 1+ŌłÜ x2 ŌłÆ1 =+ Ōł× p203, 19, 20
- 12. 3. Indeterminacions lim xŌåÆŌł× f (x)g( x) =elim [ f ( x)ŌłÆ1]┬Ęg( x) c) 1Ōł× lim xŌåÆ+Ōł×(x2 ŌłÆ3 x 2 ŌłÆ5) 3x+ 1 =1 Ōł× Sempre i quan els l├Łmits a l'infinit de f(x) i g(x) per separat siguin 1 i Ōł× respectivament.
- 13. lim xŌåÆ+Ōł×(x2 ŌłÆ3 x 2 ŌłÆ5) 3x+ 1 =1 Ōł× p204, E2, 21, 22 (x 2 ŌłÆ3 x2 ŌłÆ5 ŌłÆ1 )┬Ę(3x+1)= x 2 ŌłÆ3ŌłÆ(x 2 ŌłÆ5) x2 ŌłÆ5 ┬Ę(3x+1)= = 2┬Ę(3x+1) x2 ŌłÆ5 = 6x+2 x2 ŌłÆ5 lim xŌåÆ+Ōł×(x2 ŌłÆ3 x 2 ŌłÆ5) 3x+ 1 =e 0
- 14. 4. L├Łmits en funcions (tendint a punts concrets) a) En un punt, per l'esquerra, per la dreta lim xŌåÆ2 (x2 ŌłÆ2x+1)=22 ŌłÆ2┬Ę2+1=1 Substitu├»m valor f(x) = x2 - 2x + 1 f(x) = 2x - 1 si x<1 -x2 + 1 si x>1 lim xŌåÆ1e (2xŌłÆ1)=2┬Ę1+1=3 lim xŌåÆ1d (ŌłÆx2 +1)=ŌłÆ12 +1=0 -Un valor diferent ens indica que hi ha una discontinu├»tat de salt finit. -En aquest cas no existeix el l├Łmit tendint a 1. -No problem.
- 15. lim xŌåÆ3 x2 +1 xŌłÆ3 = 32 +1 3ŌłÆ3 = 10 0 =Ōł× El negatiu per l'esquerra ens indica que la branca va cap avall, el positiu per la dreta que la branca va cap amunt. -Ens trobem davant d'una ass├Łmptota vertical (salt infinit) f ( x)= x2 +1 xŌłÆ3 lim xŌåÆ3e x2 + 1 xŌłÆ3 = 2,92 +1 2,9ŌłÆ3 = 10 ŌłÆ0,1 =ŌłÆŌł× lim xŌåÆ3d x2 +1 xŌłÆ3 = 3,12 +1 3,1ŌłÆ3 = 10 0,1 =+Ōł×
- 16. lim xŌåÆ2 x2 ŌłÆ4 x 3 ŌłÆ7x+6 = 22 ŌłÆ4 2 3 ŌłÆ7┬Ę2+6 = 0 0 -Ens trobem davant d'una INDETERMINACI├ō 0/0!! f ( x)= x2 ŌłÆ4 x 3 ŌłÆ7x+6 Mecanisme: factoritzar i simplificar l'expressi├│. x2 ŌłÆ4 x 3 ŌłÆ7x+6 = ( x+2)( xŌłÆ2) ( xŌłÆ1)( xŌłÆ2)(x+3) = x+ 2 ( xŌłÆ1)( x+3) lim xŌåÆ2 x+2 (xŌłÆ1)(x+3) = 2+ 2 ( 2ŌłÆ1)( 2+3) = 4 5 p205, 23, 24, 25, 27, 28, 29, 63, 64, 65, 67, 71, 72, 73, 74, 75,76,79, 80, 82
- 17. b) Interpretaci├│ de cara a l'estudi de la continu├»tat Perqu├© una funci├│ sigui cont├Łnua en un punt "a" s'han de complir 3 condicions: f(a)ß┤▓ limß┤▓ a f(x) f(a)=lima f(x) ß┤▓ f(a) ß┤▓ lim f(a)=lim Gr├Āfica Cont├Łnua Ok Ok Ok Disc. evitable Ok Ok Disc. evitable Ok De salt finit Ok De salt finit De salt infinit Ok De salt infinit
- 18. 5. Rep├Ās de les funcions principals Funcions polin├▓miques Funcions racionals ( / ) Funcions amb radicals Funcions exponencials Funcions logar├Łtmiques Funcions trigonom├©triques Sempre cont├Łnues No cont├Łnues quan den=0 Sempre cont├Łnues per ├Łndex senar. En ├Łndex parell, no cont├Łnues quan radicand ├®s negatiu. Sempre cont├Łnues No cont├Łnues quan "a" ├®s 0 o negatiu (logb a) Sin i Cos cont├Łnues, Tg no en x=ŽĆ/2 + kŽĆ
- 19. "El" problema: -Estud├»a la continu├»tat de la seg├╝ent funci├│: x+1 x2 + x ŌłÜ x+ 1 f (x) = si x <= 3 si x > 3 1r: Mirar el panorama i decidir els punts d'estudi. -A la primera expressi├│ (racional) hi haur├Ā discontinu├»tat quan x2 +x=0 x2 + x = 0; x┬Ę(x + 1) = 0; x1 = 0 x2 = -1 -A la segona, tindr├Łem discontinu├»tat si x + 1 < 0. Mai ser├Ā el cas. Punts d'estudi: -1, 0, 3 (canvi), -Ōł×, +Ōł× (sempre ajuden)
- 20. 2n: Mirar qu├© passa amb l'ajuda dels l├Łmits. No existeix f(-1), per├▓ s├Ł existeix lim: DISCONTINU├ÅTAT EVITABLE lim xŌåÆŌłÆ1( x+1 x 2 +x)= ŌłÆ1+1 (ŌłÆ1) 2 +(ŌłÆ1) = 0 0 x+1 x2 + x = x+1 x( x+1) = 1 x lim xŌåÆŌłÆ1 1 x =ŌłÆ1 lim xŌåÆ0 (x+1 x 2 +x )= 0+1 0 2 +0 = 1 0 =Ōł×
- 21. No existeix f(0), l├Łmits tendeixen a infinit: AS├ŹMPTOTA VERTICAL lim xŌåÆ0 (x+1 x 2 +x )= 0+1 0 2 +0 = 1 0 =Ōł× lim xŌåÆ0e( x+1 x 2 +x)= ŌłÆ0,1+1 (ŌłÆ0,1) 2 ŌłÆ0,1 = 1 ŌłÆ0,09 =ŌłÆŌł× lim xŌåÆ0d ( x+ 1 x 2 + x)= 0,1+1 (0,1) 2 +0,1 = 1 0,11 =+Ōł×
- 22. L├Łmits per esquerra i dreta difereixen: SALT FINIT lim xŌåÆ3e( x+1 x 2 +x)= 3+ 1 3 2 + 3 = 9 12 = 1 3 lim xŌåÆ3d ŌłÜx+1=ŌłÜ 3+1=2 lim xŌåÆŌłÆŌł×( x+1 x 2 + x)=0 lim xŌåÆ+Ōł× ŌłÜ x+ 1=+ Ōł× AS├ŹMPTOTA HORITZONTAL Va creixent
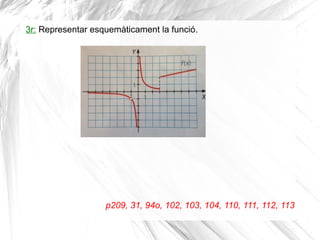
- 23. 3r: Representar esquem├Āticament la funci├│. p209, 31, 94o, 102, 103, 104, 110, 111, 112, 113
- 24. 6. Teoremes a l'entorn dels l├Łmits Si f(x) ├®s cont├Łnua en l'interval [a,b], i els signes de f(a) i f(b) s├│n diferents, podem afirmar que dins de l'interval hi ha almenys un punt c pel qual f(c)=0. Bernhard Bolzano "per for├¦a la funci├│ ha de travessar l'eix x" a) El Teorema de Bolzano
- 25. f ( x)=ŌłÜ x+1 e x + cos x xŌłÆ1 S'anul┬Ęla en algun punt de l'interval [4,6]? 1r: Comprovar que en l'interval sigui cont├Łnua: Cap de les expressions que conformen la funci├│ ens indica que no sigui cont├Łnua, per tant ├®s cont├Łnua. ŌłÜ x+ 1 ex xŌłÆ1cos x 2n: Comprovar que el valor dels extrems t├® signe oposat: f ( 4)=ŌłÜ 4+1 e 4 + cos 4 4ŌłÆ1 =ŌłÆ0,17 f (6)=ŌłÜ6+ 1 e 6 + cos6 6ŌłÆ1 =0,19 Cap de les expressions que conformen la funci├│ ens indica que no sigui cont├Łnua, per tant ├®s cont├Łnua. Signe diferent: Segons Bolzano, la funci├│ s├Ł s'anul┬Ęla en algun punt de l'interval. p210: 33, 125, p223:aplic 7 i 8
- 26. Si f(x) ├®s cont├Łnua en l'interval [a,b], f(x) pren en aquest interval tots els valors "m" entre f(a) i f(b). Jean Gaston Darboux "per for├¦a la funci├│ ha de passar per m" a) El Teorema de Darboux (o dels valors intermedis)
- 27. f ( x)=( 1ŌłÆx2 )┬Ęcos ŽĆx Existeix f(c)=-2 en algun punt c de l'interval [1,2]? 1r: Comprovar que en l'interval sigui cont├Łnua: Cap de les expressions que conformen la funci├│ ens indica que no sigui cont├Łnua, per tant ├®s cont├Łnua. 1ŌłÆx2 cosŽĆx 2n: Calcular el valor que pren la funci├│ en els extrems: Cap de les expressions que conformen la funci├│ ens indica que no sigui cont├Łnua, per tant ├®s cont├Łnua. -2 entre -3 i 0: Segons Darboux, la funci├│ s├Ł passa per -2 en algun punt de l'interval. p211: 35, 133, 134 f (1)=(1ŌłÆ12 )┬ĘcosŽĆ┬Ę1=0 f ( 2)=(1ŌłÆ22 )┬Ęcos ŽĆ┬Ę2=ŌłÆ3 -3 < -2 < 0





![2. C├Ālcul de l├Łmits.
d) Propietats de les operacions amb l├Łmits:
lim
xŌåÆ+Ōł×
[ f ( x)┬▒g( x)]= lim
xŌåÆ+ Ōł×
f ( x)┬▒ lim
xŌåÆ+Ōł×
g( x)
lim
xŌåÆ+Ōł×
[ f ( x)┬Ę g( x)]=lim
xŌåÆ+Ōł×
f ( x)┬Ę lim
xŌåÆ+ Ōł×
g( x)
lim
xŌåÆ+Ōł×
f (x)
g (x)
=
lim
xŌåÆ+ Ōł×
f ( x)
lim
xŌåÆ+ Ōł×
g( x) (si lim g(x) diferent de 0)](https://image.slidesharecdn.com/1lmitsifuncions-160927170713/85/1-Limits-i-continuitat-de-funcions-6-320.jpg)
![lim
xŌåÆ+Ōł×
p
ŌłÜ f (x)=p
ŌłÜ lim
xŌåÆ+ Ōł×
f ( x)
lim
xŌåÆ+Ōł×
[ f ( x)]p
=[ lim
xŌåÆ+Ōł×
f ( x)]p
lim
xŌåÆ+Ōł×
loga f ( x)=loga lim
xŌåÆ+Ōł×
f ( x)
lim
xŌåÆ+Ōł×
f ( x)g( x)
=( lim
xŌåÆ+Ōł×
f ( x))lim xŌåÆ+Ōł× g(x)
(si lim f(x) i lim g(x) diferent de 0)
p199: E9, 11, 12, 44 i 45 cap de setmana](https://image.slidesharecdn.com/1lmitsifuncions-160927170713/85/1-Limits-i-continuitat-de-funcions-7-320.jpg)




![3. Indeterminacions
lim
xŌåÆŌł×
f (x)g( x)
=elim [ f ( x)ŌłÆ1]┬Ęg( x)
c) 1Ōł×
lim
xŌåÆ+Ōł×(x2
ŌłÆ3
x
2
ŌłÆ5)
3x+ 1
=1
Ōł×
Sempre i quan els l├Łmits a l'infinit de f(x) i g(x) per separat siguin 1
i Ōł× respectivament.](https://image.slidesharecdn.com/1lmitsifuncions-160927170713/85/1-Limits-i-continuitat-de-funcions-12-320.jpg)










![6. Teoremes a l'entorn dels l├Łmits
Si f(x) ├®s cont├Łnua en l'interval [a,b], i els signes de f(a) i f(b) s├│n
diferents, podem afirmar que dins de l'interval hi ha almenys un
punt c pel qual f(c)=0.
Bernhard Bolzano
"per for├¦a la funci├│ ha de travessar l'eix x"
a) El Teorema de Bolzano](https://image.slidesharecdn.com/1lmitsifuncions-160927170713/85/1-Limits-i-continuitat-de-funcions-24-320.jpg)
![f ( x)=ŌłÜ x+1
e
x
+
cos x
xŌłÆ1
S'anul┬Ęla en algun punt de
l'interval [4,6]?
1r: Comprovar que en l'interval sigui cont├Łnua:
Cap de les expressions que conformen la funci├│ ens indica
que no sigui cont├Łnua, per tant ├®s cont├Łnua.
ŌłÜ x+ 1 ex
xŌłÆ1cos x
2n: Comprovar que el valor dels extrems t├® signe oposat:
f ( 4)=ŌłÜ 4+1
e
4
+
cos 4
4ŌłÆ1
=ŌłÆ0,17 f (6)=ŌłÜ6+ 1
e
6
+
cos6
6ŌłÆ1
=0,19
Cap de les expressions que conformen la funci├│ ens indica
que no sigui cont├Łnua, per tant ├®s cont├Łnua.
Signe diferent: Segons Bolzano, la funci├│ s├Ł s'anul┬Ęla en algun punt de l'interval.
p210: 33, 125, p223:aplic 7 i 8](https://image.slidesharecdn.com/1lmitsifuncions-160927170713/85/1-Limits-i-continuitat-de-funcions-25-320.jpg)
![Si f(x) ├®s cont├Łnua en l'interval [a,b], f(x) pren en aquest interval
tots els valors "m" entre f(a) i f(b).
Jean Gaston Darboux
"per for├¦a la funci├│ ha de passar per m"
a) El Teorema de Darboux (o dels valors intermedis)](https://image.slidesharecdn.com/1lmitsifuncions-160927170713/85/1-Limits-i-continuitat-de-funcions-26-320.jpg)
![f ( x)=( 1ŌłÆx2
)┬Ęcos ŽĆx Existeix f(c)=-2 en algun punt c
de l'interval [1,2]?
1r: Comprovar que en l'interval sigui cont├Łnua:
Cap de les expressions que conformen la funci├│ ens indica
que no sigui cont├Łnua, per tant ├®s cont├Łnua.
1ŌłÆx2
cosŽĆx
2n: Calcular el valor que pren la funci├│ en els extrems:
Cap de les expressions que conformen la funci├│ ens indica
que no sigui cont├Łnua, per tant ├®s cont├Łnua.
-2 entre -3 i 0: Segons Darboux, la funci├│ s├Ł passa per -2 en algun punt de l'interval.
p211: 35, 133, 134
f (1)=(1ŌłÆ12
)┬ĘcosŽĆ┬Ę1=0 f ( 2)=(1ŌłÆ22
)┬Ęcos ŽĆ┬Ę2=ŌłÆ3
-3 < -2 < 0](https://image.slidesharecdn.com/1lmitsifuncions-160927170713/85/1-Limits-i-continuitat-de-funcions-27-320.jpg)