1 resource radian measure and arc length
Download as PPTX, PDF3 likes2,597 views
This document discusses radian measure and its use in measuring angles and arcs in circles. It defines a radian as the angle subtended at the center of a circle by an arc equal in length to the radius. The document provides formulas for converting between radian and degree measures. Specifically, it states that 1 radian is equal to 180/ŽĆ degrees, or approximately 57.3 degrees. Examples are given to demonstrate calculating radian measures given arc lengths and radii, and to convert between radians and degrees.
1 of 12
Downloaded 160 times











Recommended
2 circular measure arc length



2 circular measure arc lengthLily Maryati
╠²
The document discusses calculating arc length and the area of a sector of a circle. It defines that the arc length s is equal to the radius r multiplied by the central angle ╬Ė in radians. The area of a sector is equal to (1/2) * r^2 * ╬Ė, where ╬Ė is in radians. It provides examples of calculating arc length when given r and ╬Ė, and the area of sectors when given r and the central angle measure.Mensuration ppt



Mensuration pptcooliohan
╠²
The document provides formulas for calculating the surface area of various 3D geometric shapes like cubes, cuboids, spheres, cylinders, cones, and combinations of shapes. The key information summarized is:
1) Formulas are given for surface area of individual shapes like cubes (6a^2), cuboids (2(lb+lh+bh)), spheres (4ŽĆr^2), cylinders (2ŽĆrh+2ŽĆr^2), and cones (ŽĆr(l+2h)).
2) Formulas are also provided for combinations of shapes, for example when two cubes are joined to form a cuboid the surface area is 10a^2.
3) In general,Expressions and equations



Expressions and equationsAron Dotson
╠²
The document discusses translating verbal phrases into algebraic expressions and using verbal models to write mathematical equations and inequalities. It provides examples of common verbal phrases involving numbers, operations, and variables and their corresponding algebraic translations. It also outlines a three-step process for writing a mathematical model from a word problem: 1) write a verbal model, 2) assign labels, and 3) write the algebraic model. Finally, it demonstrates this process with a sample word problem about the cost of dim sum plates after tax.Mathematics- Circle Presentation



Mathematics- Circle PresentationMonnie Bao Jia
╠²
This document defines key terms and formulas related to circles, including circumference, diameter, radius, area, arcs, sectors, segments, chords, and semicircles. It provides formulas for calculating the circumference, area, arc length, area of sectors and segments, chord length, perimeter and area of semicircles. Examples are included to demonstrate how to apply the formulas to solve geometry problems involving circles.Radians



Radiansevypace
╠²
Radians are a unit of measurement used to describe angles and arcs in circles. A radian is defined as the ratio between the length of an arc and its radius, where a full circle contains 2ŽĆ radians. While degrees are a more common unit, with 360 degrees in a full circle, radians provide a consistent unit of measurement around any size circle based on its radius. The document also provides formulas for converting between radians and degrees.Surds



SurdsAng Choon Cheng
╠²
This document discusses working with surds, which are expressions involving square roots. It provides rules for multiplying, dividing, adding, subtracting, and simplifying surds. Some key rules covered are combining like terms under a square root, rationalizing denominators by multiplying the numerator and denominator by the conjugate of the denominator, and squaring both sides of an equation to clear surds before solving. Examples are provided to demonstrate applying these rules to simplify expressions and solve equations involving surds.2.5.6 Perpendicular and Angle Bisectors



2.5.6 Perpendicular and Angle Bisectorssmiller5
╠²
* Construct perpendicular and angle bisectors
* Use bisectors to solve problems
* Identify the circumcenter and incenter of a triangleTrigonometry for class xi



Trigonometry for class xiindu psthakur
╠²
1. The document provides the weightage or marks distribution for different units in Class XI. The highest weightage is given to Algebra with 37 marks, followed by Sets and Functions with 29 marks.
2. The document then provides definitions and derivations of some fundamental trigonometric identities involving sine, cosine, tangent, cotangent, secant and cosecant functions. Key identities such as sin^2(╬Ė) + cos^2(╬Ė) = 1 are derived from basic definitions.
3. Suggestions are provided for proving trigonometric identities which include starting from one side and making it look like the other side, using pythagorean identities, and expressing everything in terms of sine andSurface area of sphere - Mathematics



Surface area of sphere - MathematicsLet's Tute
╠²
This is a session dedicated to three dimensional shapes namely 'SPHERE' & 'HEMISPHERE'. It's designed to explain the concept of surface area for both of these shapes using real life examples
Following are the subtopics covered here:
1. What is Sphere ?
2. Surface area of a sphere
3. Surface area of a hollow hemisphere
4. Surface area of a solid hemisphereDistributive property in algebra power point



Distributive property in algebra power pointChristie Harp
╠²
The document discusses the distributive property in algebra. The distributive property allows terms inside parentheses to be distributed so that expressions can be simplified out of order from the standard order of operations. It involves multiplying the number outside of the parentheses by each term inside the parentheses. Examples are provided to demonstrate how to use the distributive property to simplify expressions.7.2 Similar Polygons



7.2 Similar Polygonssmiller5
╠²
The student is able to identify scale factors and use them to solve problems involving similar polygons. Scale factors allow comparison of corresponding side lengths of similar polygons through proportions. To determine if two polygons are similar, their corresponding angles must be congruent and side lengths must be proportional as shown through equal ratios.Slope formula



Slope formulacoolhanddav
╠²
This document provides examples for calculating slope using the slope formula. It demonstrates how to find slope given two points on a line, from a graph or table, and from a linear equation. It also explains that slope represents rate of change and gives examples where slope describes things like plant growth rate or electricity cost increase over time.Linear equations in two variables- By- Pragyan



Linear equations in two variables- By- PragyanPragyan Poudyal
╠²
This is a power point presentation on linear equations in two variables for class 10th. I have spent 3 hours on making this and all the equations you will see are written by me.Circular measures



Circular measuresSruthi Krishna
╠²
The document discusses key concepts relating to circles such as:
1) The perimeter of a circle is 2ŽĆr, where r is the radius of the circle.
2) An arc is part of a circle, and the central angle of an arc is the angle formed by the endpoints of the arc and the center of the circle.
3) The area of a circle can be calculated as ŽĆr^2, where r is the radius.Circles 9th



Circles 9thMeha Kapoor
╠²
This document defines key terms related to circles such as radius, diameter, chord, arc, and semicircle. It explains that a circle is a closed curve where all points are equidistant from the center. A radius is a line from the center to the edge, a diameter goes through the center and connects two points on the edge, and a chord connects any two points on the edge. An arc is part of the edge between two points, and a semicircle is half of the full circle. The document also describes properties of these terms like diameters being the longest chords and radii all being the same length.Matrices and System of Linear Equations ppt



Matrices and System of Linear Equations pptDrazzer_Dhruv
╠²
The document discusses matrices and systems of linear equations. It defines matrices and different types of matrices including square, diagonal, scalar, identity, zero, negative, upper triangular, lower triangular, and transpose matrices. It also covers properties of matrix operations and examples of finding the transpose of matrices. The document then discusses row echelon form (REF) and reduced row echelon form (RREF) as well as the different types of solutions that systems of linear equations can have.properties of exponents



properties of exponentsOrlando Calderon
╠²
The document summarizes properties of exponents including the product, power, and quotient properties. It provides examples of applying each property to simplify exponential expressions. For example, it shows that the product property allows rewriting (-5)4 * (-5)5 as (-5)4+5 = (-5)9 = -1953125. It also introduces scientific notation and provides an example of rewriting 131,400,000,000 as 1.314 x 1011 by moving the decimal 11 places to the right.Areas of Circles and Sectors



Areas of Circles and Sectorscogleysclass
╠²
The document discusses calculating the areas of circles, sectors, and segments of circles. It defines a circle as having the area of ŽĆr^2, a sector as a fractional part of the total circle area defined by an arc and its radii, and a segment as the portion of a sector minus the area of the triangle formed by the arc and its radii. It provides examples of calculating the areas of full circles, sectors of varying central angles, and segments.Factorising Quadratics



Factorising QuadraticsMr C
╠²
The document provides instructions on factorizing quadratic equations. It begins by explaining what quadratic equations are and provides examples. It then discusses factorizing quadratics where the coefficient of x^2 is 1 by finding two numbers whose product is the last term and sum is the middle term. The document continues explaining how to factorize when the coefficient of x^2 is not 1 and predicts the signs of the factors based on the signs of the terms in the quadratic equation. It provides examples of factorizing different quadratic equations.The Sine Ratio



The Sine RatioPassy World
╠²
When a plane descends for landing, its flight path forms a right triangle with its speed and angle determining the hypotenuse. There are four formulas for working with sine triangles: opposite side equals hypotenuse multiplied by sine of the angle; angle equals inverse sine of opposite over hypotenuse; hypotenuse equals opposite divided by sine of the angle; and calculators use the sine and inverse sine buttons set to degrees mode. Solving sine triangle problems involves labeling sides, identifying the unknown, and applying the appropriate formula while substituting values and rounding answers.Arithmetic and Geometric Progressions 



Arithmetic and Geometric Progressions Dr. Tushar J Bhatt
╠²
This presentation covered following topics :
1. Introduction
2. Arithmetic Progression (AP)
3. Sum of Series in AP
4. Arithmetic and Geometric Mean
5. Geometric Progression (GP)
6. Sum of Series in GP
7. Relation Between AM, GM and HM
and is useful for B.Com and BBA students. Trigonometric Function Of Any Angle



Trigonometric Function Of Any Angleguest793408
╠²
The document defines trigonometric functions for any angle using ratios based on the coordinates of a point on the terminal side of the angle. It introduces the concept of a reference angle, which is the acute angle formed by the terminal side and the x-axis, and explains how to use reference angles to evaluate trigonometric functions for non-acute angles by determining the sign from the quadrant. An example problem demonstrates evaluating trigonometric functions using a reference angle.Dalil Proyeksi



Dalil Proyeksinadsca
╠²
Dokumen tersebut menjelaskan tentang dalil proyeksi pada segitiga. Dalil proyeksi digunakan untuk menentukan panjang sisi segitiga dengan cara memproyeksikan salah satu sisinya ke sisi lainnya. Rumus dalil proyeksi untuk segitiga lancip diperoleh dengan menggabungkan teorema Pythagoras dan panjang hasil proyeksi, sedangkan untuk segitiga tumpul dengan menambahkan panjang hasil proyeksi.bisector-and-perpendicular-line-lesson-19.pptx



bisector-and-perpendicular-line-lesson-19.pptxFelix Jones Banares
╠²
The document defines and proves theorems about the distance from a point to a line and the perpendicular bisector of a line segment. It shows that:
1) A point on the bisector of an angle is equidistant from the sides of the angle.
2) A point equidistant from the sides of an angle lies on the bisector of the angle.
3) A point on the perpendicular bisector of a segment is equidistant from the endpoints of the segment.
4) A point equidistant from the endpoints of a segment lies on the perpendicular bisector of the segment.6.1 Radian Measure



6.1 Radian Measuresmiller5
╠²
Convert between degrees and radians
Find the length of an intercepted arc
Find the area of a sector4. ap gp



4. ap gpPSIT kanpur
╠²
This document discusses arithmetic and geometric progressions. It defines arithmetic and geometric sequences as lists of numbers where each subsequent term is calculated using a common difference or ratio. It provides formulas to calculate the nth term and sum of the first n terms for both progressions. The document also discusses arithmetic and geometric means as the averages between two numbers in an arithmetic or geometric progression.Pythagoras Theorem Explained



Pythagoras Theorem ExplainedPassy World
╠²
Pythagoras discovered that the ancient Egyptians used a 3:4:5 right triangle to build the pyramids. He investigated this further and deduced the Pythagorean theorem, which states that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Pythagoras proved this by drawing squares on each side of right triangles and showing that the areas added up. The Pythagorean theorem has been used since ancient times in architecture, engineering, and more recently in technology like screens.Radians And Arc Length



Radians And Arc LengthYelena Melnichenko
╠²
1. Radian measure relates the angle measure to the arc length intercepted by the angle on a circle of radius r. If the arc length is equal to r, the angle measure is 1 radian.
2. To use formulas for arc length and area of a sector, the angle measure must be in radians. The document provides conversions between degrees and radians and examples of using the arc length and area formulas.
3. The key ideas are that radian measure relates the angle to arc length on a circle, and formulas require the angle be in radians rather than degrees. Examples show converting between degrees and radians and using the formulas.More Related Content
What's hot (20)
Surface area of sphere - Mathematics



Surface area of sphere - MathematicsLet's Tute
╠²
This is a session dedicated to three dimensional shapes namely 'SPHERE' & 'HEMISPHERE'. It's designed to explain the concept of surface area for both of these shapes using real life examples
Following are the subtopics covered here:
1. What is Sphere ?
2. Surface area of a sphere
3. Surface area of a hollow hemisphere
4. Surface area of a solid hemisphereDistributive property in algebra power point



Distributive property in algebra power pointChristie Harp
╠²
The document discusses the distributive property in algebra. The distributive property allows terms inside parentheses to be distributed so that expressions can be simplified out of order from the standard order of operations. It involves multiplying the number outside of the parentheses by each term inside the parentheses. Examples are provided to demonstrate how to use the distributive property to simplify expressions.7.2 Similar Polygons



7.2 Similar Polygonssmiller5
╠²
The student is able to identify scale factors and use them to solve problems involving similar polygons. Scale factors allow comparison of corresponding side lengths of similar polygons through proportions. To determine if two polygons are similar, their corresponding angles must be congruent and side lengths must be proportional as shown through equal ratios.Slope formula



Slope formulacoolhanddav
╠²
This document provides examples for calculating slope using the slope formula. It demonstrates how to find slope given two points on a line, from a graph or table, and from a linear equation. It also explains that slope represents rate of change and gives examples where slope describes things like plant growth rate or electricity cost increase over time.Linear equations in two variables- By- Pragyan



Linear equations in two variables- By- PragyanPragyan Poudyal
╠²
This is a power point presentation on linear equations in two variables for class 10th. I have spent 3 hours on making this and all the equations you will see are written by me.Circular measures



Circular measuresSruthi Krishna
╠²
The document discusses key concepts relating to circles such as:
1) The perimeter of a circle is 2ŽĆr, where r is the radius of the circle.
2) An arc is part of a circle, and the central angle of an arc is the angle formed by the endpoints of the arc and the center of the circle.
3) The area of a circle can be calculated as ŽĆr^2, where r is the radius.Circles 9th



Circles 9thMeha Kapoor
╠²
This document defines key terms related to circles such as radius, diameter, chord, arc, and semicircle. It explains that a circle is a closed curve where all points are equidistant from the center. A radius is a line from the center to the edge, a diameter goes through the center and connects two points on the edge, and a chord connects any two points on the edge. An arc is part of the edge between two points, and a semicircle is half of the full circle. The document also describes properties of these terms like diameters being the longest chords and radii all being the same length.Matrices and System of Linear Equations ppt



Matrices and System of Linear Equations pptDrazzer_Dhruv
╠²
The document discusses matrices and systems of linear equations. It defines matrices and different types of matrices including square, diagonal, scalar, identity, zero, negative, upper triangular, lower triangular, and transpose matrices. It also covers properties of matrix operations and examples of finding the transpose of matrices. The document then discusses row echelon form (REF) and reduced row echelon form (RREF) as well as the different types of solutions that systems of linear equations can have.properties of exponents



properties of exponentsOrlando Calderon
╠²
The document summarizes properties of exponents including the product, power, and quotient properties. It provides examples of applying each property to simplify exponential expressions. For example, it shows that the product property allows rewriting (-5)4 * (-5)5 as (-5)4+5 = (-5)9 = -1953125. It also introduces scientific notation and provides an example of rewriting 131,400,000,000 as 1.314 x 1011 by moving the decimal 11 places to the right.Areas of Circles and Sectors



Areas of Circles and Sectorscogleysclass
╠²
The document discusses calculating the areas of circles, sectors, and segments of circles. It defines a circle as having the area of ŽĆr^2, a sector as a fractional part of the total circle area defined by an arc and its radii, and a segment as the portion of a sector minus the area of the triangle formed by the arc and its radii. It provides examples of calculating the areas of full circles, sectors of varying central angles, and segments.Factorising Quadratics



Factorising QuadraticsMr C
╠²
The document provides instructions on factorizing quadratic equations. It begins by explaining what quadratic equations are and provides examples. It then discusses factorizing quadratics where the coefficient of x^2 is 1 by finding two numbers whose product is the last term and sum is the middle term. The document continues explaining how to factorize when the coefficient of x^2 is not 1 and predicts the signs of the factors based on the signs of the terms in the quadratic equation. It provides examples of factorizing different quadratic equations.The Sine Ratio



The Sine RatioPassy World
╠²
When a plane descends for landing, its flight path forms a right triangle with its speed and angle determining the hypotenuse. There are four formulas for working with sine triangles: opposite side equals hypotenuse multiplied by sine of the angle; angle equals inverse sine of opposite over hypotenuse; hypotenuse equals opposite divided by sine of the angle; and calculators use the sine and inverse sine buttons set to degrees mode. Solving sine triangle problems involves labeling sides, identifying the unknown, and applying the appropriate formula while substituting values and rounding answers.Arithmetic and Geometric Progressions 



Arithmetic and Geometric Progressions Dr. Tushar J Bhatt
╠²
This presentation covered following topics :
1. Introduction
2. Arithmetic Progression (AP)
3. Sum of Series in AP
4. Arithmetic and Geometric Mean
5. Geometric Progression (GP)
6. Sum of Series in GP
7. Relation Between AM, GM and HM
and is useful for B.Com and BBA students. Trigonometric Function Of Any Angle



Trigonometric Function Of Any Angleguest793408
╠²
The document defines trigonometric functions for any angle using ratios based on the coordinates of a point on the terminal side of the angle. It introduces the concept of a reference angle, which is the acute angle formed by the terminal side and the x-axis, and explains how to use reference angles to evaluate trigonometric functions for non-acute angles by determining the sign from the quadrant. An example problem demonstrates evaluating trigonometric functions using a reference angle.Dalil Proyeksi



Dalil Proyeksinadsca
╠²
Dokumen tersebut menjelaskan tentang dalil proyeksi pada segitiga. Dalil proyeksi digunakan untuk menentukan panjang sisi segitiga dengan cara memproyeksikan salah satu sisinya ke sisi lainnya. Rumus dalil proyeksi untuk segitiga lancip diperoleh dengan menggabungkan teorema Pythagoras dan panjang hasil proyeksi, sedangkan untuk segitiga tumpul dengan menambahkan panjang hasil proyeksi.bisector-and-perpendicular-line-lesson-19.pptx



bisector-and-perpendicular-line-lesson-19.pptxFelix Jones Banares
╠²
The document defines and proves theorems about the distance from a point to a line and the perpendicular bisector of a line segment. It shows that:
1) A point on the bisector of an angle is equidistant from the sides of the angle.
2) A point equidistant from the sides of an angle lies on the bisector of the angle.
3) A point on the perpendicular bisector of a segment is equidistant from the endpoints of the segment.
4) A point equidistant from the endpoints of a segment lies on the perpendicular bisector of the segment.6.1 Radian Measure



6.1 Radian Measuresmiller5
╠²
Convert between degrees and radians
Find the length of an intercepted arc
Find the area of a sector4. ap gp



4. ap gpPSIT kanpur
╠²
This document discusses arithmetic and geometric progressions. It defines arithmetic and geometric sequences as lists of numbers where each subsequent term is calculated using a common difference or ratio. It provides formulas to calculate the nth term and sum of the first n terms for both progressions. The document also discusses arithmetic and geometric means as the averages between two numbers in an arithmetic or geometric progression.Pythagoras Theorem Explained



Pythagoras Theorem ExplainedPassy World
╠²
Pythagoras discovered that the ancient Egyptians used a 3:4:5 right triangle to build the pyramids. He investigated this further and deduced the Pythagorean theorem, which states that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Pythagoras proved this by drawing squares on each side of right triangles and showing that the areas added up. The Pythagorean theorem has been used since ancient times in architecture, engineering, and more recently in technology like screens.Similar to 1 resource radian measure and arc length (20)
Radians And Arc Length



Radians And Arc LengthYelena Melnichenko
╠²
1. Radian measure relates the angle measure to the arc length intercepted by the angle on a circle of radius r. If the arc length is equal to r, the angle measure is 1 radian.
2. To use formulas for arc length and area of a sector, the angle measure must be in radians. The document provides conversions between degrees and radians and examples of using the arc length and area formulas.
3. The key ideas are that radian measure relates the angle to arc length on a circle, and formulas require the angle be in radians rather than degrees. Examples show converting between degrees and radians and using the formulas.Areas related to circle



Areas related to circleSatwantKaur20
╠²
1) A circle is defined as the set of all points in a plane that are equidistant from a fixed point called the center.
2) Key terms related to circles include radius, diameter, chord, arc, sector, and segment. The radius connects the center to any point on the circle, while the diameter connects two points on the circle and passes through the center.
3) The area of a circle is calculated as ŽĆr^2, where r is the radius. The area of a sector of a circle is calculated based on the central angle in radians that the sector spans.Radius Methods to Calculate the Radius of a Circle.pdf



Radius Methods to Calculate the Radius of a Circle.pdfChloe Cheney
╠²
Learn what radius is by definition and discover four methods to calculate the radius of the circleŌĆöpractice given examples and other questions.Circles&sphere



Circles&sphereJenyap
╠²
The document discusses geometric shapes related to circles such as spheres, hemispheres, and sectors. It provides formulas for calculating the surface area and volume of spheres and hemispheres. Formulas are given for finding the circumference, area, radius, and arc length of circles. Methods for calculating the area of sectors and segments of circles are also presented. Worked examples demonstrate how to apply the formulas to solve related problems.Circles&sphere



Circles&spherejygwen
╠²
The document discusses geometric shapes related to circles such as spheres, hemispheres, and sectors. It provides formulas for calculating the surface area and volume of spheres and hemispheres. Formulas are given for finding the circumference, area, and radii of circles. The document also discusses converting between degrees and radians and formulas for calculating arc length, area of sectors, and area of segments of circles.Circles & Sphere



Circles & Spherevaylu
╠²
The document discusses geometric shapes related to circles such as spheres, hemispheres, and sectors. It provides formulas for calculating the surface area and volume of spheres and hemispheres. Formulas are given for finding the circumference, area, and radii of circles. The document also discusses converting between degrees and radians and formulas for calculating arc length, area of sectors, and area of segments of circles.Circlessphere



CirclessphereJennifer Chong
╠²
The document discusses geometric shapes related to circles such as spheres, hemispheres, and sectors. It provides formulas for calculating the surface area and volume of spheres and hemispheres. Formulas are given for finding the circumference, area, and radii of circles. The document also discusses converting between degrees and radians and formulas for calculating arc length, area of sectors, and area of segments of circles.Circle & sphere



Circle & sphereJ─▒a Y─▒─▒
╠²
The document discusses geometric shapes related to circles such as spheres, hemispheres, and sectors. It provides formulas for calculating the surface area and volume of spheres and hemispheres. Formulas are given for finding the circumference, area, and radii of circles. The document also discusses converting between degrees and radians and provides formulas for calculating arc length, area of sectors, and area of segments of circles.Fundamentals of Trigonometry.pdf



Fundamentals of Trigonometry.pdfNusratIqbal9
╠²
This document provides an overview of fundamentals of trigonometry including:
- There are two main types of trigonometry - plane and spherical trigonometry. Plane trigonometry deals with angles and triangles in a plane, while spherical trigonometry deals with triangles on a sphere.
- An angle is defined as the union of two rays with a common endpoint, and can be measured in degrees or radians. There are four quadrants used to classify angles in the Cartesian plane.
- The trigonometric ratios of sine, cosine, and tangent are defined based on the sides of a right triangle containing the angle of interest. These ratios are fundamental functions in trigonometry.maths TRIGONOMETRIC FUNCTIONS



maths TRIGONOMETRIC FUNCTIONSSurya Swaroop
╠²
This document discusses trigonometric functions. It begins by defining trigonometric functions as generalizations of trigonometric ratios to any angle measure, in terms of radian measure. It defines the six trigonometric functions - sine, cosine, tangent, cotangent, secant, and cosecant - in terms of the x-coordinate and y-coordinate of a point on a unit circle. Key properties discussed include the periodic nature of the functions and their values for quadrantal and other common angles.Areas related to circle, Chapter-10



Areas related to circle, Chapter-10Siddu Lingesh
╠²
This document summarizes key concepts related to circles for a 10th grade class. It covers the perimeter and area of circles, finding the area of sectors and segments of circles, and calculating the areas of combinations of plane figures. The perimeter of a circle is called its circumference, which is 2ŽĆr. The area of a circle is ŽĆr^2. To find the area of a sector, use the formula (╬Ė/360)├ŚŽĆr^2, where ╬Ė is the central angle of the sector in degrees and r is the radius. The area of combinations of shapes can be found by subtracting the area of one figure from another or adding/subtracting different areas.Physics a2 unit4_05_circular_motion_01 phyiscs circular motion



Physics a2 unit4_05_circular_motion_01 phyiscs circular motionsashrilisdi
╠²
This document defines key terms related to angular displacement, velocity, and rotation. It discusses:
1) The relationship between degrees and radians and defines angular displacement as the number of radians moved.
2) Angular velocity as the rate of change of angular displacement over time, measured in radians per second.
3) The connection between angular velocity, period of rotation, and frequency, where angular velocity equals 2ŽĆ divided by the period.
4) How to calculate linear speed from angular velocity and radius of rotation.Velocidad angular, lineal



Velocidad angular, linealYadi Campos
╠²
This document discusses concepts related to circular motion including arc length, angular velocity, and linear velocity. It defines arc length as the portion of a circle measured in linear units, which can be calculated using the formula L=R╬Ė where L is arc length, R is radius, and ╬Ė is the central angle in radians. Angular velocity is defined as the angle turned per unit of time and its formula is presented. Linear velocity is the speed an object moves along a circular path, which is equal to the product of angular velocity and radius. Several example problems are worked through applying these concepts and formulas.MC-MATH-3-TRIGONOMETRY.pdf



MC-MATH-3-TRIGONOMETRY.pdfLIBARDORONELYNPORIO
╠²
The document discusses the radian measure for measuring angles and converting between degrees and radians. It defines a radian as the central angle that subtends an arc with length equal to the radius. The formula for arc length is given as s=r╬Ė, where s is arc length, r is radius, and ╬Ė is the radian measure. Examples are provided for converting degrees to radians by multiplying degrees by ŽĆ/180, and radians to degrees by multiplying radians by 180/ŽĆ. Practice problems are included at the end to convert between the units and find arc lengths and radii.Chapter 8 circular measure



Chapter 8 circular measureatiqah ayie
╠²
This document provides information about circular measure including radians, conversion between radians and degrees, length of arc, and area of sectors. It defines a radian as the angle subtended by an arc equal in length to the radius. Formulas are given for converting between radians and degrees, finding the length of an arc given the radian measure of its central angle, and finding the area of a sector given its radian measure and the radius. Several examples demonstrate applying these formulas to solve problems involving radians. Exercises provide additional practice problems for students to work through.Circles 02 



Circles 02 justerjobs
╠²
Circle class 10 cbse ppt for teachers student for online and offline class, contact 9753223223 To need more ppt11-6 circles.ppt



11-6 circles.pptFernanbocol
╠²
This document provides information about calculating the area of circles. It defines circumference and diameter, and presents the formulas for calculating the circumference and area of a circle using pi and the radius. It includes examples of using the area formula to calculate the area when given the radius or diameter. The final challenge is to calculate the area of a donut by finding the area of the larger circle and subtracting the area of the smaller circle.Physics a2 unit4_05_circular_motion_01- circular motion



Physics a2 unit4_05_circular_motion_01- circular motionsashrilisdi
╠²
This document defines key terms related to angular displacement, velocity, and motion. It explains that angles can be measured in degrees or radians, with 360┬░ equal to 2ŽĆ radians. Angular displacement is the angle an object rotates through, measured in radians. Angular velocity is the rate of change of the angular displacement with respect to time. Angular velocity and period are related to frequency, as angular velocity equals 2ŽĆ divided by the period. Linear speed can also be calculated from angular velocity and radius of rotation. Examples are provided to illustrate these relationships and calculations.Areas related to Circles - class 10 maths 



Areas related to Circles - class 10 maths Amit Choube
╠²
This a ppt which is based on chapter circles of class 10 maths it is a very good ppt which will definitely enhance your knowledge . it will also clear all concepts and doubts about this chapter and its topics More from Lily Maryati (11)
Trigonometry - SPA Program



Trigonometry - SPA ProgramLily Maryati
╠²
It features brief explanation of Trigonometry and some revision along with answer key. This presentation aims to provide additional exercise for home revision.How statistics used in real world



How statistics used in real worldLily Maryati
╠²
Statistics has been considered as an mundane topic of Mathematics in high school. This presentation shows some practical examples of application of statistics data in marketing strategy.Integration of function on non standard form



Integration of function on non standard formLily Maryati
╠²
This presentation explains how to integrate functions which do not fall into standard form. The presentation is taken from Introducing Pure Mathematics - OXFORDInequalities quadratic, fractional & irrational form



Inequalities quadratic, fractional & irrational formLily Maryati
╠²
To solve quadratic, fractional, irrational, and absolute value inequalities, one should:
1. Make the right-hand side zero by shifting terms to the left-hand side
2. Fully factorize the left-hand side to find critical values
3. Draw a sign diagram for the left-hand side using the critical values
4. Determine the range of values for the variable based on the sign diagram.Quadratic Equations



Quadratic EquationsLily Maryati
╠²
This presentation includes the roots of quadratic equation, the nature of the roots, minimum and maximum values and quadratic inequalityApplication of differentiation



Application of differentiationLily Maryati
╠²
This presentation explains how the differentiation is applied to identify increasing and decreasing functions,identifying the nature of stationary points and also finding maximum or minimum values.Relative velocity introduction



Relative velocity introductionLily Maryati
╠²
The document discusses true velocity and relative velocity. It defines true velocity as the velocity of a moving object relative to the earth. It explains that the apparent path of an object depends on the observer's frame of reference. It provides examples of how to calculate relative velocity between two moving objects by using an equation and drawing a velocity diagram.Inequalities



InequalitiesLily Maryati
╠²
This document outlines procedures for solving quadratic, fractional, and irrational inequalities. It describes making the right-hand side zero, fully factorizing the left-hand side to find critical values, drawing a sign diagram, and determining the range of values from the sign diagram. Examples are provided for finding the range of values for given inequalities of each type.Vectors in 2 Dimensions



Vectors in 2 DimensionsLily Maryati
╠²
Vectors in 2D describes scalar and vector quantities. Scalar quantities only have magnitude, while vector quantities have both magnitude and direction. The document explains that two ships sailing the same distance but with different bearings will not end up at the same place, and an airplane traveling the same speed but in different directions will also not reach the same destination. It also demonstrates how to find the magnitude of a vector using the Pythagorean theorem and defines two vectors as equal if they have the same magnitude and direction.Further trigonometry identities



Further trigonometry identitiesLily Maryati
╠²
This presentation shows how sum and difference of angles formula are derived. It also features doubled-angled formula and other trigonometry formulas.Equation of a Circle



Equation of a CircleLily Maryati
╠²
1) The document discusses the equation of a circle and how to derive it using the Pythagorean theorem and distance formula.
2) For a circle with center (0,0), the equation is x^2 + y^2 = r^2, where r is the radius.
3) More generally, for a circle with center (a,b), the equation is (x-a)^2 + (y-b)^2 = r^2, where (a,b) are the coordinates of the center and r is the radius.Recently uploaded (20)
How to Configure Recurring Revenue in Odoo 17 CRM



How to Configure Recurring Revenue in Odoo 17 CRMCeline George
╠²
This slide will represent how to configure Recurring revenue. Recurring revenue are the income generated at a particular interval. Typically, the interval can be monthly, yearly, or we can customize the intervals for a product or service based on its subscription or contract. Inventory Reporting in Odoo 17 - Odoo 17 Inventory App



Inventory Reporting in Odoo 17 - Odoo 17 Inventory AppCeline George
╠²
This slide will helps us to efficiently create detailed reports of different records defined in its modules, both analytical and quantitative, with Odoo 17 ERP.Oral exam Kenneth Bech - What is the meaning of strategic fit?



Oral exam Kenneth Bech - What is the meaning of strategic fit?MIPLM
╠²
Presentation of the CEIPI DU IPBA oral exam of Kenneth Bech - What is the meaning of strategic fit? Intellectual Honesty & Research Integrity.pptx



Intellectual Honesty & Research Integrity.pptxNidhiSharma495177
╠²
Research Publication & Ethics contains a chapter on Intellectual Honesty and Research Integrity.
Different case studies of intellectual dishonesty and integrity were discussed.Azure Data Engineer Interview Questions By ScholarHat



Azure Data Engineer Interview Questions By ScholarHatScholarhat
╠²
Azure Data Engineer Interview Questions By ScholarHatRRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)



RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)SONU HEETSON
╠²
RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper. MMV MCQ PDF Free Download for Railway Assistant Loco Pilot Exam.AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
╠²
AI and Academic Writing, Short Term Course in Academic Writing and Publication, UGC-MMTTC, MANUU, 25/02/2025, Prof. (Dr.) Vinod Kumar Kanvaria, University of Delhi, vinodpr111@gmail.comBlind spots in AI and Formulation Science, IFPAC 2025.pdf



Blind spots in AI and Formulation Science, IFPAC 2025.pdfAjaz Hussain
╠²
The intersection of AI and pharmaceutical formulation science highlights significant blind spotsŌĆösystemic gaps in pharmaceutical development, regulatory oversight, quality assurance, and the ethical use of AIŌĆöthat could jeopardize patient safety and undermine public trust. To move forward effectively, we must address these normalized blind spots, which may arise from outdated assumptions, errors, gaps in previous knowledge, and biases in language or regulatory inertia. This is essential to ensure that AI and formulation science are developed as tools for patient-centered and ethical healthcare.Odoo 18 Accounting Access Rights - Odoo 18 ║▌║▌▀Żs



Odoo 18 Accounting Access Rights - Odoo 18 ║▌║▌▀ŻsCeline George
╠²
In this slide, weŌĆÖll discuss on accounting access rights in odoo 18. To ensure data security and maintain confidentiality, Odoo provides a robust access rights system that allows administrators to control who can access and modify accounting data. How to Configure Deliver Content by Email in Odoo 18 Sales



How to Configure Deliver Content by Email in Odoo 18 SalesCeline George
╠²
In this slide, weŌĆÖll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.Bß╗ś TEST KIß╗éM TRA GIß╗«A K├ī 2 - TIß║ŠNG ANH 10,11,12 - CHUß║©N FORM 2025 - GLOBAL SU...



Bß╗ś TEST KIß╗éM TRA GIß╗«A K├ī 2 - TIß║ŠNG ANH 10,11,12 - CHUß║©N FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
╠²
https://app.box.com/s/ij1ty3vm7el9i4qfrr41o756xycbahmgASP.NET Web API Interview Questions By Scholarhat



ASP.NET Web API Interview Questions By ScholarhatScholarhat
╠²
ASP.NET Web API Interview Questions By ScholarhatComprehensive Guide to Antibiotics & Beta-Lactam Antibiotics.pptx



Comprehensive Guide to Antibiotics & Beta-Lactam Antibiotics.pptxSamruddhi Khonde
╠²
¤ōó Comprehensive Guide to Antibiotics & Beta-Lactam Antibiotics
¤ö¼ Antibiotics have revolutionized medicine, playing a crucial role in combating bacterial infections. Among them, Beta-Lactam antibiotics remain the most widely used class due to their effectiveness against Gram-positive and Gram-negative bacteria. This guide provides a detailed overview of their history, classification, chemical structures, mode of action, resistance mechanisms, SAR, and clinical applications.
¤ōī What YouŌĆÖll Learn in This Presentation
Ō£ģ History & Evolution of Antibiotics
Ō£ģ Cell Wall Structure of Gram-Positive & Gram-Negative Bacteria
Ō£ģ Beta-Lactam Antibiotics: Classification & Subtypes
Ō£ģ Penicillins, Cephalosporins, Carbapenems & Monobactams
Ō£ģ Mode of Action (MOA) & Structure-Activity Relationship (SAR)
Ō£ģ Beta-Lactamase Inhibitors & Resistance Mechanisms
Ō£ģ Clinical Applications & Challenges.
¤ÜĆ Why You Should Check This Out?
Essential for pharmacy, medical & life sciences students.
Provides insights into antibiotic resistance & pharmaceutical trends.
Useful for healthcare professionals & researchers in drug discovery.
¤æē Swipe through & explore the world of antibiotics today!
¤öö Like, Share & Follow for more in-depth pharma insights!Full-Stack .NET Developer Interview Questions PDF By ScholarHat



Full-Stack .NET Developer Interview Questions PDF By ScholarHatScholarhat
╠²
Full-Stack .NET Developer Interview Questions PDF By ScholarHatDr. Ansari Khurshid Ahmed- Factors affecting Validity of a Test.pptx



Dr. Ansari Khurshid Ahmed- Factors affecting Validity of a Test.pptxKhurshid Ahmed Ansari
╠²
Validity is an important characteristic of a test. A test having low validity is of little use. Validity is the accuracy with which a test measures whatever it is supposed to measure. Validity can be low, moderate or high. There are many factors which affect the validity of a test. If these factors are controlled, then the validity of the test can be maintained to a high level. In the power point presentation, factors affecting validity are discussed with the help of concrete examples.AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
╠²
Bß╗ś TEST KIß╗éM TRA GIß╗«A K├ī 2 - TIß║ŠNG ANH 10,11,12 - CHUß║©N FORM 2025 - GLOBAL SU...



Bß╗ś TEST KIß╗éM TRA GIß╗«A K├ī 2 - TIß║ŠNG ANH 10,11,12 - CHUß║©N FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
╠²
1 resource radian measure and arc length
- 1. Radian measureArc lengthArea of sectorRadian measure use in trigonometryCircular Measure
- 2. Properties of A CircleWhat do we know about Circle?Minor SectorArcArea = ŽĆr2Circumference = 2ŽĆr/ ŽĆd
- 3. Finding Arc Length & Area of Sector
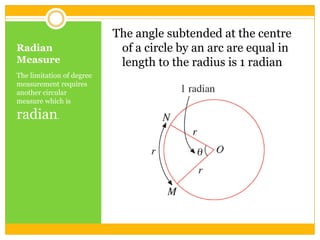
- 4. Radian MeasureThe limitation of degree measurement requires another circular measure which is radian.The angle subtended at the centre of a circle by an arc are equal in length to the radius is 1 radian
- 5. Radian MeasureLength of arc APC = 2rLength of arc APD = 3rLength of arc APE = 3.6r’āÉAOC = 2 radians’āÉAOD = 3 radians’āÉAOE = 3.6 radiansSo, how do we determine the radian measure given the arc length and the radius of the circle?
- 6. Radian MeasureIn general, if the length of arc, s units and the radius is r units, then That is the size of the angle (╬Ė) is given by the ratio of the arc length to the length of the radius.For example:If s = 3 cm and r = 2 cm, then
- 7. Relation between Radian and Degree MeasureConsider the angle ╬Ė in a semicircle of radius r as shown below. Then,We can concludeFurthermore,
- 8. Convertion between Degree & RadianDEGREERADIAN
- 9. Relation between Radian and Degree MeasureExample 1:Solution:
- 10. Relation between Radian and Degree MeasureExample 2:Solution:
- 11. Classwork
- 12. ReferencesThong, Ho Soo, Msc, Dip Ed; Hiong, Khor Nyak, Bsc, Dip Ed; ŌĆ£New Additional MathematicsŌĆØ pg. 280 - 292, SNP Panpac Pte Ltd, Singapore 2005.







