はし?めてのハ?ターン認識輪読会 10章後半
- 1. はじパタ輪読会 ? 10章後半(10.4) 確率モデルによるクラスタリング ? 2014/3/4 ? @_kobacky
- 2. 最初のおことわり m(_ ?_)m ?? 本資料は教科書を読んで最初????だった ? @_kobacky ?のような人が勉強するためのとっかかり となることを目標とします。 ? ?? そのため、なるべく分布を図示して考えたいです。 そこで教科書では ?d次元のデータについて論じられ ていますが、図や例は一次元データで考えて作成し ています。平均ベクトルとか共分散行列は一旦置い といて、平均値?分散値で考えさせて下さい。 ? ?? 本資料は一部、教科書に記載のない、作成者の解釈 による内容を含んでいます。
- 3. 【STEP1】10.4.1 ?節と全体像 そもそも確率モデルとは何か?確率モデルによるクラ スタリングとは何をすることなのか理解しましょう。 ? ? 【目標!】 ? ?? ハードクラスタリングとの違いを理解する ? ?? 確率モデルについて理解する ? ?? 混合正規分布とそのパラメータについて理解する ? ?? 確率モデルによるクラスタリングとは具体的に何を 求めることなのかについて理解する ?
- 4. 確率モデルによるクラスタリング ?? ハードクラスタリング ? ?? 一つのデータは一つのクラスタにのみ分類される ? ?? クラスタリング結果例 ? ?? データ1はクラスタA ? ?? データ2はクラスタB ? ?? 確率モデルによるクラスタリング ? ?? 所属するクラスタは確率的に定められる ? ?? クラスタリング結果例 ?(クラスタ数 ?= ?3) ? ?? データ1はクラスタ [A,B,C] ?に ?[0.8,0.1,0.1] ?の確率で 所属する ? ?? データ2はクラスタ [A,B,C] ?に ?[0.1,0.3,0.6] ?の確率で 所属する ? ?? 「確率モデル」ってなんすか??(次ページ) ?
- 5. クラスタリングにおける確率モデル ?? モデルとして仮定するもの ? 1.? クラスタ毎のデータ分布モデル ? 2.? [1] ?の線形和によって表現される全体のデータ分布モデル ? ?? よく使われるのは混合正規分布モデル ? (%) ? ? モデルの例 ? ?一次元正規分布 ? ?3クラスタ ? x ?: ?観測データ ?
- 6. 混合正規分布モデルのパラメータ ?? 各クラスタの正規分布パラメータ ? ?? μk ?: ?平均 ? ?? Σk ?: ?分散(標準偏差でも可) ? ?? 混合するために必要なパラメータ ? ?? πk ?: ?クラスタ毎の正規分布の混合比 ? 混合正規分布 クラスタ1 ? = ?π1 ?× ? 分散:Σ1 ? ? クラスタ3 ? + ? ?π3 ?× ? + ? ?π2 ?× ? 平均:μ1 ? ? せん?けい?わ! ? クラスタ2 ? 平均:μ2 ? ? 分散:Σ2 ? ? 平均:μ3 ? ? 分散:Σ3 ? ?
- 7. ちなみに?? ?? 本資料の確率モデル図はExcel ?で下記の通り作成 ? ?? 9パラメータでモデルが決定しているのがわかる ? ?? パラメータを色々変えてモデルの変化をみると面白い かも?? ? ?? こちらから ?DL ?可能 ?-?‐> ?hNp://bit.ly/1eJCa4i ? ?
- 8. 確率モデル(混合正規分布モデル) ? によるクラスタリングとは? ?? 下記の2つを行うこと ? 1.? 観測データを最もよく表現する確率モデルを推定 ? ?? 確率モデルのパラメータ推定(平均?分散?混合比) ? 2.? 推定したモデルによって各データのクラスタを推定 ? ?? 各データが各クラスタに所属する確率の演算 ? ?? 演算する確率の数は ?[データ数] ?× ?[クラスタ数] ? ? ?? [1][2]の推定を交互に実施し、最適なモデル推定を行 うのが ?EM ?アルゴリズム(後述) ? x1 ?: ?[A,B,C] ?= ?[0.8, ?0.1, ?0.1] ? x2 ?: ?[A,B,C] ?= ?[0.1, ?0.6, ?0.3] ? x3 ?: ?[A,B,C] ?= ?[0.3, ?0.3, ?0.4] [1]Mステップ [2]Eステップ
- 9. 【STEP2】10.4.2 ?節?10.4.4 ?節 確率モデルの推定、確率モデルを用いたクラスタリン グを実施するための準備。 ? そのための各種定義について理解しましょう。 ? ? 【目標!】 ? ?? 各データが所属するクラスタの状態を表現するため の隠れ変数について理解する ?? モデルパラメータの最尤推定を実施するために?? ?? 完全データの定義について理解する ? ?? 確率モデルの尤度について理解する ? ?? 確率モデルのパラメータを最尤推定するための Q ?関数につ いて理解する ?
- 10. 隠れ変数 ?? 実際に観測されたデータがどのクラスタに属するか 表現するためのベクトル変数 ? ??z ?= ?(z1,z2,z3,???,zK) ? ?? K ?: ?クラスタ数 ? ?? データがクラスタk ?に所属している状態の場合 ? ??z ?= ?(0,0,0,?,1,??,0) ? ?→ ?zk ?= ?1 ? k番目 ?? p(zk ?= ?1) ?= ?πk ? ?? モデル条件下で、k ?番目のクラスタに所属する確 率はそのクラスタの混合比に一致するため。(教科 書には記載無し。@_kobacky ?による解釈。)
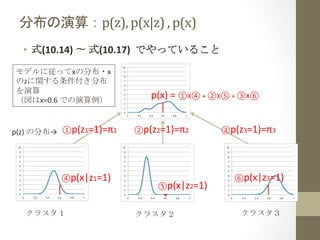
- 11. 分布の演算:p(z), ?p(x|z) ?, ?p(x) ?? 式(10.14) ?? ?式(10.17) ? ?でやっていること ? モデルに従ってxの分布?x のzに関する条件付き分布 を演算 ? (図はx=0.6 ?での演算例) ? p(z) ?の分布→ ? ①p(z1=1)=π1 ? ? ④p(x|z1=1) ? ? クラスタ1 ? p(x) ?= ?①X④ ?+ ?②X⑤ ?+ ?③X⑥ ? ? ②p(z2=1)=π2 ? ? ⑤p(x|z2=1) ? ? クラスタ2 ? ③p(z3=1)=π3 ? ? ⑥p(x|z3=1) ? ? クラスタ3 ?
- 12. 隠れ変数の事後確率:γ(zk) ?? 式(10.18)の演算:γ(z) ?= ?p(z) ?× ?p(x ?| ?z) ?/ ?p(x) ? k=1 ?(クラスタ1)の場合 ? γ(z1) ?= ?①X④ ?/ ?⑦ ? ? p(z) ?の分布→ ? ①p(z1=1)=π1 ? ? ④p(x|z1=1) ? ? クラスタ1 ? ⑦ ?p(x) ?= ?①X④ ?+ ?②X⑤ ?+ ?③X⑥ ? ? ②p(z2=1)=π2 ? ? ⑤p(x|z2=1) ? ? クラスタ2 ? ③p(z3=1)=π3 ? ? ⑥p(x|z3=1) ? ? クラスタ3 ?
- 13. 隠れ変数の事後確率:γ(zk) ?? 式(10.18)の演算:γ(z) ?= ?p(z) ?× ?p(x ?| ?z) ?/ ?p(x) ? k=2 ?(クラスタ2)の場合 ? γ(z2) ?= ?②X⑤ ?/ ?⑦ ? ? p(z) ?の分布→ ? ①p(z1=1)=π1 ? ? ④p(x|z1=1) ? ? クラスタ1 ? ⑦ ?p(x) ?= ?①X④ ?+ ?②X⑤ ?+ ?③X⑥ ? ? ②p(z2=1)=π2 ? ? ⑤p(x|z2=1) ? ? クラスタ2 ? ③p(z3=1)=π3 ? ? ⑥p(x|z3=1) ? ? クラスタ3 ?
- 14. 隠れ変数の事後確率:γ(zk) ?? 式(10.18)の演算:γ(z) ?= ?p(z) ?× ?p(x ?| ?z) ?/ ?p(x) ? k=3 ?(クラスタ3)の場合 ? γ(z3) ?= ?③X⑥ ?/ ?⑦ ? ? p(z) ?の分布→ ? ①p(z1=1)=π1 ? ? ④p(x|z1=1) ? ? クラスタ1 ? ⑦ ?p(x) ?= ?①X④ ?+ ?②X⑤ ?+ ?③X⑥ ? ? ②p(z2=1)=π2 ? ? ⑤p(x|z2=1) ? ? クラスタ2 ? ③p(z3=1)=π3 ? ? ⑥p(x|z3=1) ? ? クラスタ3 ?
- 15. 隠れ変数に関連して考えたこと ?? データx ?の隠れ変数z ?(zk=1)に関する事後確率は、こ のモデルにおいて ?x ?が ?k番目のクラスタに所属する 確率を示している。 ? ?? ?前頁までの例において、Σk=1,2,3(γ(zk)) ?= ?1 ?となること がわかる。
- 16. 完全データ ?? データの集合:X ? ?? X ?= ?(x1,x2,???,xN) ? ? ?xi ?= ?(xi1,xi2,???,xid)の転置ベクトル ? ?? 隠れ変数の集合:Z ? ?? Z ?= ?(z1,z2,???,zN) ? ? ?zi ?= ?(zi1,zi2,???,ziK)の転置ベクトル ? ?? 変数定義 ? ?? N ?: ?観測データの個数 ? ?? d ?: ?観測データの次元数 ? ?? K ?: ?クラスタ数 ? ?? 完全データ:Y ? ?? Y ?= ?(X,Z) ? ?? データと隠れ変数を合わせた集合
- 17. 完全データの尤度 ?? 完全データの尤度が最大となるように確率モデルに おけるパラメータを最適化する。 ? ?? 完全データの尤度 ? ?? Y ?= ?(X,Z) ?の同時確率 ? 式 ?(10.19) ? 特定の隠れ変数集合が ? 生起する確率 xi ?がクラスタk ?に属す る場合のxi ?生起確率 特定の隠れ変数集合下で 観測データが観測される 確率 確率的に定まる ?0 ?or ?1
- 18. 完全データの対数尤度 ?? 最尤推定値を求めるために対数尤度関数に変換 ? ?? 確率分布関数は対数を取った方が微分しやすい(最尤推定 に関する詳細は ?4.3節 参照) ? z ?? ただし隠れ変数 ik ?は確率的に定まるため、この対数尤度 関数から直接最尤推定値を求めることはできない。 ? ?? 最尤推定:観測データから、最も尤もらしいモデルのパラ メータを推定する。 ? 式 ?(10.20) ? 1かもしれないし、 ? 0かもしれない。
- 19. Q ?関数 ?? Q ?関数 ? ?? 対数尤度関数の、隠れ変数に関する期待値 ? ?? 対数尤度関数の代わりに最尤推定に用いる ? 式 ?(10.21) ? zik ?の zik ?に関する ? 期待値 式 ?(10.22) ? Zik ?= ?0 ?の項は全て ?0 ?になり、 zik= ?1 ?の項のみ残る 隠れ変数 zi ?の事後確率
- 20. Q ?関数 式 ?(10.23) ? モデルが決定すれば 値が定まる
- 21. 【STEP3】10.4.5 ?節?10.4.7 ?節 確率モデルのパラメータ推定の方法について学びます。 ? ? 【目標!】 ? ?? EM ?アルゴリズムの考え方を理解する ? ?? 「EM ?アルゴリズムのパラメータ推定が ?Q ?関数の微 分を使ってできるんだなぁ??へぇ?」と思う ? ?? カルバック?ライブラー情報量とは何かを知る ? ?? EM ?アルゴリズムにより、モデルによる分布と真の 分布が近づいて行くイメージを持つ ?
- 22. EM ?アルゴリズム ?? 確率モデルのパラメータの最尤推定値を求める手法 ? ?? 2種類のステップを交互に実施 ? 1.? Expectafon ?ステップ(③) ? ?? 確率モデルのパラメータを固定 ? ?? 固定された確率モデル下における隠れ変数の事後確率を演算 ? 2.? Maximizafon ?ステップ(①②) ? ?? E ?ステップで得た隠れ変数の事後確率を ?Q ?関数に代入 ? ?? Q ?関数を最大にする ?(確率モデルの)パラメータを求める ? ?? Q ?関数の対数尤度が収束するまで繰り返す ? ?? 局所解には注意。初期値を変えて何度か実施すると良い。 γ11 ?= ?0.3, ?γ12 ?= ?0.4, ?γ13 ?= ?0.3 ? γ21 ?= ?0.6, ?γ22 ?= ?0.1, ?γ23 ?= ?0.3 ? γ31 ?= ?0.2, ?γ32 ?= ?0.7, ?γ33 ?= ?0.1 ? ①代入 ③演算 ②パラメータ 最尤値推定 Q関数が ? 収束したら 完
- 23. EM ?アルゴリズムの式 ?? E ?ステップ ? ?? M ?ステップ ? k番目のクラスタ に属するデータ数 の推定値 平均?分散?混合比 の定義に対して納得 感のある式になって いると思う。
- 24. EM ?アルゴリズムの式の導出 ???は、割愛します。 ? 気になる方は ?10.4.6 ?節をご参照下さい。 ?m(_ ?_)m ? ?? μk ?や Σk ?の推定は、 ?Q ?関数の(推定対象パラメータに よる)偏微分 ?= ?0 ?となるようなパラメータを求めるこ とで行う。 ? ?? πk ?の推定はラグランジュ関数とか使ってなんかやっ てます。。 ?
- 25. EM ?アルゴリズムの性質(1) ?? p(X|θ) ?= ?p(X,Z) ?/ ?p(Z|X, ?θ) ? ? ?? ?? ?? ?? X ?: 観測データ集合 ? Z ?: 観測データ集合X ?に対する隠れ変数集合 ? θ ?: 確率モデルのパラメータ集合 ? p(X ?| ?θ):パラメータθの確率モデル下における観測データX の尤度 ? ?? 対数尤度 ?= ?lnp(X|θ) ?= ???? ?= ?L(q|θ) ?+ ?KL(q||p) ? ?? q(Z) ?: ?Z ?に関する任意の分布 ? ?? L(q|θ) ?= ?ΣZq(Z)ln(p(X,Z|θ) ?/ ?q(Z)) ? ?? KL(q||p) ?= ?ΣZq(Z)ln(q(Z) ?/ ?p(Z|X,θ)) ? ?? カルバック?ライブラー情報量 ? ?? 真の分布q(Z) ?と ?(確率モデル?観測データを元に得られる)事後 分布p(Z|X,θ) ?の確率変数間の距離(正の値)を表す ?
- 26. EM ?アルゴリズムの性質(2) ?? L(q|θ) ?を最大化することで、KL(q||p) ?を小さくする、 つまり、p(モデルによる隠れ変数の分布)をq(真の分 布)に近づける。 ? ?? E ?ステップではθを固定して ?q ?に関して L(q|θ) ?を最大化 ? ?? M ?ステップでは最大化されたqを用いてθに関してL(q|θ)を最 大化。 ? ?? モデルによる隠れ変数の分布が真の分布に近づく。 ? EステップではL ?を最大化す ることでこのラインを上に 押し上げたい! ? ?? ステップ毎にQ関数の値が大きくなることが示されている。 ?
- 27. ありがとうございました!




![確率モデルによるクラスタリング
?? ハードクラスタリング
?
?? 一つのデータは一つのクラスタにのみ分類される
?
?? クラスタリング結果例
?
?? データ1はクラスタA
?
?? データ2はクラスタB
?
?? 確率モデルによるクラスタリング
?
?? 所属するクラスタは確率的に定められる
?
?? クラスタリング結果例
?(クラスタ数
?=
?3)
?
?? データ1はクラスタ
[A,B,C]
?に
?[0.8,0.1,0.1]
?の確率で
所属する
?
?? データ2はクラスタ
[A,B,C]
?に
?[0.1,0.3,0.6]
?の確率で
所属する
?
?? 「確率モデル」ってなんすか??(次ページ)
?](https://image.slidesharecdn.com/10-140304101559-phpapp01/85/10-4-320.jpg)
![クラスタリングにおける確率モデル
?? モデルとして仮定するもの
?
1.? クラスタ毎のデータ分布モデル
?
2.? [1]
?の線形和によって表現される全体のデータ分布モデル
?
?? よく使われるのは混合正規分布モデル
?
(%)
?
?
モデルの例
?
?一次元正規分布
?
?3クラスタ
?
x
?:
?観測データ
?](https://image.slidesharecdn.com/10-140304101559-phpapp01/85/10-5-320.jpg)


![確率モデル(混合正規分布モデル)
?
によるクラスタリングとは?
?? 下記の2つを行うこと
?
1.? 観測データを最もよく表現する確率モデルを推定
?
?? 確率モデルのパラメータ推定(平均?分散?混合比)
?
2.? 推定したモデルによって各データのクラスタを推定
?
?? 各データが各クラスタに所属する確率の演算
?
?? 演算する確率の数は
?[データ数]
?×
?[クラスタ数]
?
?
?? [1][2]の推定を交互に実施し、最適なモデル推定を行
うのが
?EM
?アルゴリズム(後述)
?
x1
?:
?[A,B,C]
?=
?[0.8,
?0.1,
?0.1]
?
x2
?:
?[A,B,C]
?=
?[0.1,
?0.6,
?0.3]
?
x3
?:
?[A,B,C]
?=
?[0.3,
?0.3,
?0.4]
[1]Mステップ
[2]Eステップ](https://image.slidesharecdn.com/10-140304101559-phpapp01/85/10-8-320.jpg)