10 buku-rancob-uji lanjutan
- 1. 173 BAB X UJI LANJUTAN 10.1 Teori dan Analisis Secara Manual Analisis data yang telah dilakukan akan menghasilkan kesimpulan apakah Ho atau H1 yang diterima setelah dilakukan uji F, untuk mengetahui apakah terdapat perbedaan perlakuan yang dicobakan. H0 : ╬╝1 = ╬╝2 = ╬╝3 = ╬╝4 ŌĆ”ŌĆ”.= ╬╝n H1 : ╬╝1 ŌēĀ ╬╝2 ŌēĀ ╬╝3 ŌēĀ ╬╝4 ŌĆ”ŌĆ”. ŌēĀ ╬╝n Atau sekurang-kurangnya ada sepasang yang tidak sama Jika Ho diterima berarti semua perlakuan yang dicobakan memberikan pengaruh yang sama, tetapi jika H1 yang diterima berarti paling sedikit terdapat sepasang nilai tengah perlakuan yang berbeda. Untuk mengetahui pasangan perlakuan mana yang mempunyai nilai tengah yang berbeda tersebut, maka perlu dilakukan pengujian lanjutan untuk mengetahui perbedaan diantara nilai tengah perlakuan tersebut. Pengujian tersebut diistilahkan dengan uji lanjutan atau biasa juga disebut uji pembanding berganda atau Untuk melakukan uji lanjutan, digunakan beberapa jenis uji lanjutan. Setiap jenis uji lanjutan memerlukan kriteria-kriteria tertentu yang harus dipenuhi sehingga pengunaannya tidak boleh sembarang. Beberapa jenis uji lanjutan yang dapat digunakan antara lain: uji Beda Nyata Terkecil (BNT), uji Beda Nyata Jujur (BNJ), uji Student
- 2. NeumanŌĆÖs Keuls (SNK), uji DuncanŌĆÖs Multiple Range Test (DMRT), uji DunnetŌĆÖs, uji Scheffe, dan lain-lain. Penggunaan uji lanjutan digunakan untuk mengetahui pasangan perlakuan mana yang mempunyai nilai tengah yang berbeda. Untuk menentukan jenis uji lanjutan yang sesuai maka harus diperhatikan apakah uji yang akan digunakan adalah untuk perbandingan yang bersifat terencana atau tidak. Perbandingan terencana adalah perbandingan yang memang direncanakan sebelum data suatu percobaan diperoleh atau sebelum percobaan dilakukan, sedangkan perbandingan tidak terencana adalah perbandingan yang dilakukan setelah data diperoleh. Beberapa uji lanjutan yang sering digunakan adalah 174 sebagai berikut: 1. Uji Beda Nyata Terkecil (BNT) Salah satu prosedur uji yang paling sederhana untuk menjawab pertanyaan tentang nilai tengah perlakuan mana yang berbeda apabila H1 diterima adalah uji beda nyata terkecil (Least Significant Different = LSD). Uji ini sangat cocok digunakan apabila pengujian nilai tengah perlakuan yang akan dibandingkan sebelumnya telah direncanakan. Tingkat ketepatan uji BNT akan berkurang jika digunakan untuk menguji semua kemungkinan pasangan nilai tengah perlakuan (melakukan pembanding yang tidak terencana). Beberapa aturan dasar yang perlu diperhatikan agar uji
- 3. ini dapat digunakan secara efektif antara lain: gunakan uji BNT hanya apabila F. Hitung > F. Tabel, tidak menggunakan uji BNT untuk membandingkan semua kombinasi pasangan nilai tengah perlakuan karena hanya cocok untuk membandingkan dengan kontrol atau tidak lebih dari lima perlakuan. Apabila setiap perlakuan mempunyai ulangan yang sama yaitu r, maka formula untuk perhitungan nilai pembanding (NP) BNT pada taraf nyata ╬▒ adalah: 175 NP BNT╬▒ = t╬▒ . ŌłÜ( Ē¤É Ēæ▓Ēæ╗ Ēæ«ĒÆéĒÆŹĒÆéĒÆĢ) Ēɽ Nilai t╬▒ dilihat pada tabel t dengan menggunakan derajat bebas galat dan ╬▒ yang digunakan. Untuk menilai apakah dua nilai tengah perlakuan berbeda secara statistika, maka bandingkan dengan selisih (beda) dua nilai tengah perlakuan tersebut dengan nilai BNT. Jika beda dua nilai tengah > nilai BNT , maka dua nilai tengah dikatakan berbeda secara nyata pada taraf ╬▒, sebaliknya jika beda dua nilai tengah Ōēż nilai NP BNT, maka dua nilai tengah dikatakan tidak berbeda nyata. 2. Uji Beda Nyata Jujur (BNJ) Uji beda nyata jujur (BNJ) sering juga disebut uji Turkey (Honestly Significant Difference = HSD). Tidak seperti penggunaan uji BNT, uji BNJ dapat digunakan untuk membandingkan semua pasangan perlakuan yang ada.
- 4. Penggunaan uji ini sangat sederhana karena hanya menggunakan satu nilai untuk menguji semua kombinasi perlakuan yang akan dibandingkan seperti halnya pada uji BNT. Kriterium uji BNJ sama dengan uji BNT. Apabila setiap perlakuan mempunyai ulangan yang sama yaitu r, maka formula untuk perhitungan nilai BNJ pada taraf nyata ╬▒ adalah: 176 NP BNJ╬▒ = q╬▒ (p, fe). ŌłÜ( Ēæ▓Ēæ╗ Ēæ«ĒÆéĒÆŹĒÆéĒÆĢ) Ēɽ Nilai q╬▒ dilihat pada tabel BNJ dimana p adalah jumlah perlakuan dan fe adalah derajat bebas galat. 3. Uji Student NeumanŌĆÖs Keuls (SNK), Uji Student NeumanŌĆÖs Keuls , sering juga disebut uji SNK. Tidak seperti penggunaan uji BNT, SNK hampir sama dengan uji BNJ, dapat digunakan untuk membandingkan semua pasangan perlakuan yang ada. Penggunaan uji ini sangat sederhana karena hanya menggunakan satu nilai untuk menguji semua kombinasi perlakuan yang akan dibandingkan seperti halnya pada uji BNT dan uji BNJ. Kriterium uji SNK sama dengan uji BNT dan uji BNJ. Apabila setiap perlakuan mempunyai ulangan yang sama yaitu r, maka formula untuk perhitungan nilai SNK pada taraf nyata ╬▒ adalah: NP SNK╬▒ = q╬▒ (p, fe). ŌłÜ( Ēæ▓Ēæ╗ Ēæ«ĒÆéĒÆŹĒÆéĒÆĢ) Ēɽ
- 5. Nilai q╬▒ dilihat pada tabel q dimana p adalah jumlah perlakuan dan fe adalah derajat bebas galat. 10.2 Analisis Dengan menggunakan Program SPSS 177 a. Uji Beda Nyata Terkecil (BNT) Data Yang akan dianalisis Uji Lanjutan LSD KELOMPOK PERLAKUAN I II III JUMLAH P0 7.83 7.63 8.28 23.74 P1 8.95 9.38 10.55 28.88 P2 11.1 13.45 10.83 35.38 P3 9.23 8.18 9.55 26.96 JUMLAH 37.11 38.64 39.21 114.96 1. Buka Program SPSS, akan muncul tampilan berikut ini
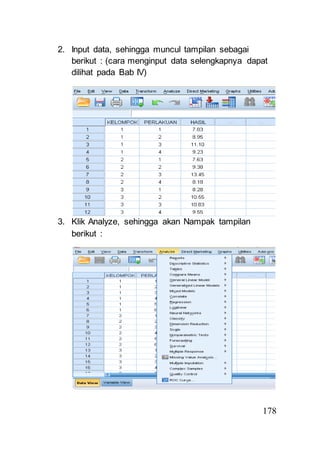
- 6. 178 2. Input data, sehingga muncul tampilan sebagai berikut : (cara menginput data selengkapnya dapat dilihat pada Bab IV) 3. Klik Analyze, sehingga akan Nampak tampilan berikut :
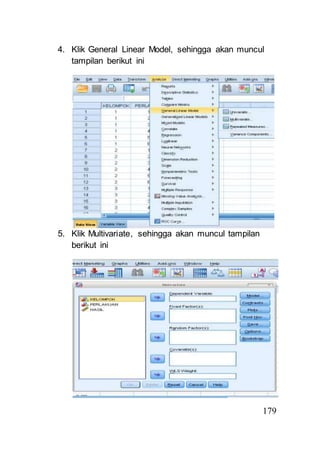
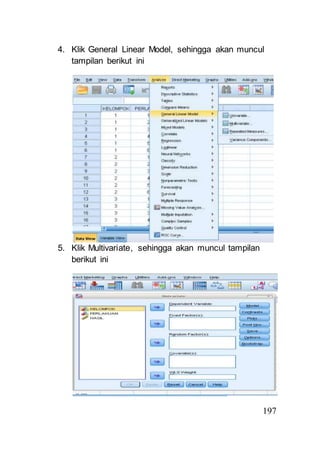
- 7. 4. Klik General Linear Model, sehingga akan muncul 179 tampilan berikut ini 5. Klik Multivariate, sehingga akan muncul tampilan berikut ini
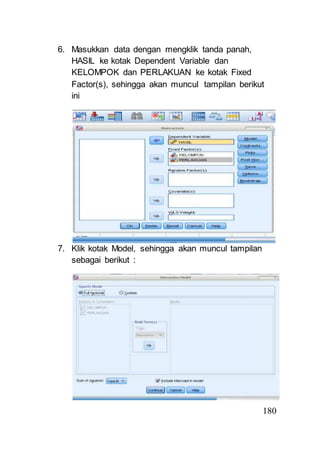
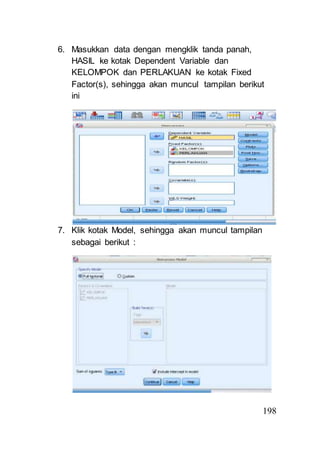
- 8. 180 6. Masukkan data dengan mengklik tanda panah, HASIL ke kotak Dependent Variable dan KELOMPOK dan PERLAKUAN ke kotak Fixed Factor(s), sehingga akan muncul tampilan berikut ini 7. Klik kotak Model, sehingga akan muncul tampilan sebagai berikut :
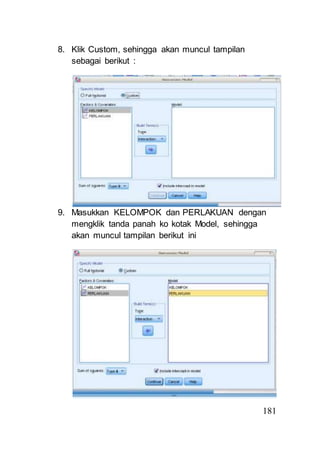
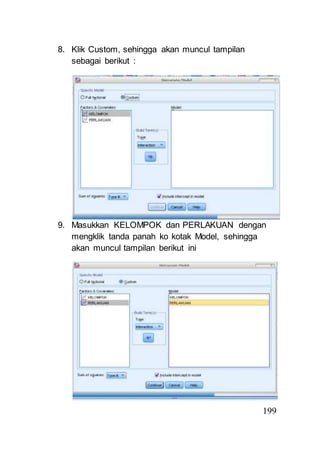
- 9. 181 8. Klik Custom, sehingga akan muncul tampilan sebagai berikut : 9. Masukkan KELOMPOK dan PERLAKUAN dengan mengklik tanda panah ko kotak Model, sehingga akan muncul tampilan berikut ini
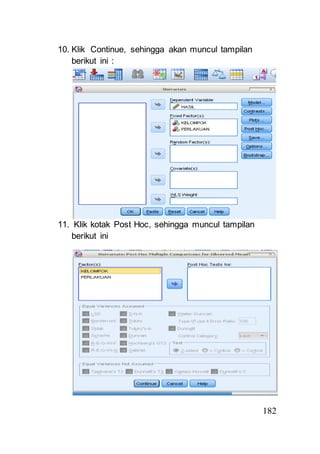
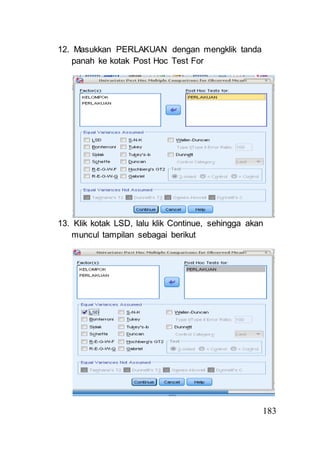
- 10. 182 10. Klik Continue, sehingga akan muncul tampilan berikut ini : 11. Klik kotak Post Hoc, sehingga muncul tampilan berikut ini
- 11. 183 12. Masukkan PERLAKUAN dengan mengklik tanda panah ke kotak Post Hoc Test For 13. Klik kotak LSD, lalu klik Continue, sehingga akan muncul tampilan sebagai berikut
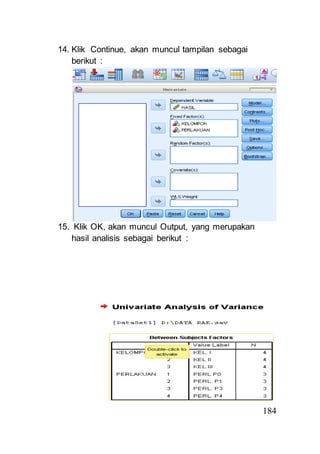
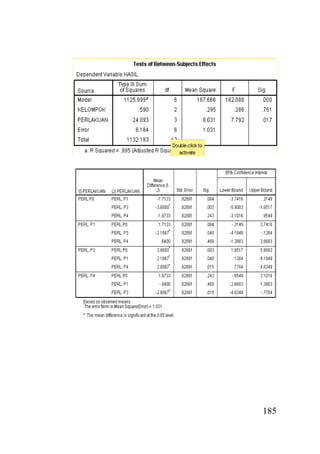
- 12. 184 14. Klik Continue, akan muncul tampilan sebagai berikut : 15. Klik OK, akan muncul Output, yang merupakan hasil analisis sebagai berikut :
- 13. 185
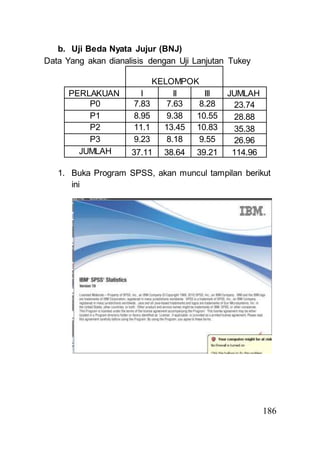
- 14. 186 b. Uji Beda Nyata Jujur (BNJ) Data Yang akan dianalisis dengan Uji Lanjutan Tukey KELOMPOK PERLAKUAN I II III JUMLAH P0 7.83 7.63 8.28 23.74 P1 8.95 9.38 10.55 28.88 P2 11.1 13.45 10.83 35.38 P3 9.23 8.18 9.55 26.96 JUMLAH 37.11 38.64 39.21 114.96 1. Buka Program SPSS, akan muncul tampilan berikut ini
- 15. 187 2. Input data, sehingga muncul tampilan sebagai berikut ( langkah-langkah menginput data yang lebih lengkap, dapat dilihat pada Bab IV): 3. Klik Analyze, sehingga akan Nampak tampilan berikut :
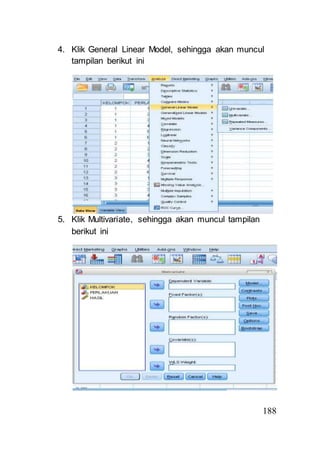
- 16. 4. Klik General Linear Model, sehingga akan muncul 188 tampilan berikut ini 5. Klik Multivariate, sehingga akan muncul tampilan berikut ini
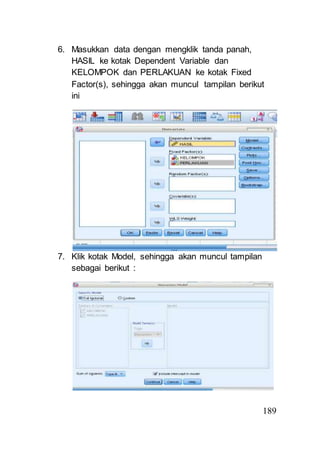
- 17. 189 6. Masukkan data dengan mengklik tanda panah, HASIL ke kotak Dependent Variable dan KELOMPOK dan PERLAKUAN ke kotak Fixed Factor(s), sehingga akan muncul tampilan berikut ini 7. Klik kotak Model, sehingga akan muncul tampilan sebagai berikut :
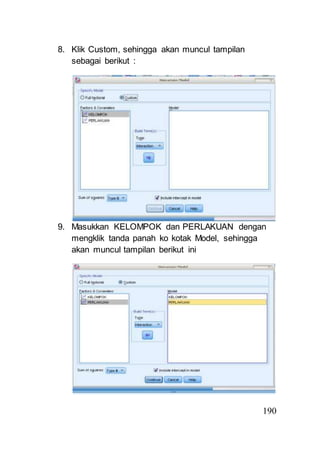
- 18. 190 8. Klik Custom, sehingga akan muncul tampilan sebagai berikut : 9. Masukkan KELOMPOK dan PERLAKUAN dengan mengklik tanda panah ko kotak Model, sehingga akan muncul tampilan berikut ini
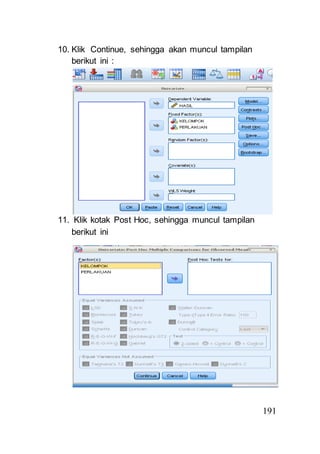
- 19. 191 10. Klik Continue, sehingga akan muncul tampilan berikut ini : 11. Klik kotak Post Hoc, sehingga muncul tampilan berikut ini
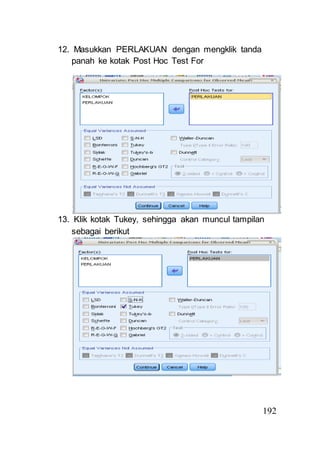
- 20. 192 12. Masukkan PERLAKUAN dengan mengklik tanda panah ke kotak Post Hoc Test For 13. Klik kotak Tukey, sehingga akan muncul tampilan sebagai berikut
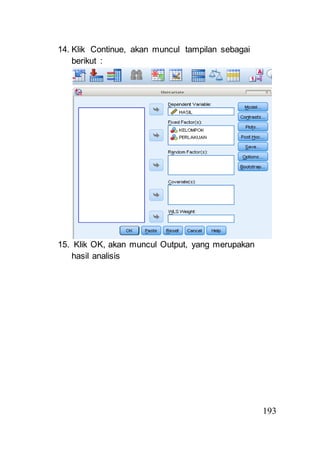
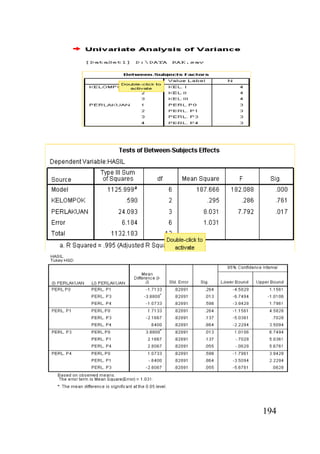
- 21. 193 14. Klik Continue, akan muncul tampilan sebagai berikut : 15. Klik OK, akan muncul Output, yang merupakan hasil analisis
- 22. 194
- 23. 195 c. Uji Student NeumanŌĆÖs Keuls (SNK), Data Yang akan dianalisis dengan Uji Lanjutan SNK KELOMPOK PERLAKUAN I II III JUMLAH P0 7.83 7.63 8.28 23.74 P1 8.95 9.38 10.55 28.88 P2 11.1 13.45 10.83 35.38 P3 9.23 8.18 9.55 26.96 JUMLAH 37.11 38.64 39.21 114.96 1. Buka Program SPSS, akan muncul tampilan berikut ini
- 24. 196 2. Input data, sehingga muncul tampilan sebagai berikut (input data yang lengkap dapat dilihat pada Bab IV): 3. Klik Analyze, sehingga akan Nampak tampilan berikut :
- 25. 4. Klik General Linear Model, sehingga akan muncul 197 tampilan berikut ini 5. Klik Multivariate, sehingga akan muncul tampilan berikut ini
- 26. 198 6. Masukkan data dengan mengklik tanda panah, HASIL ke kotak Dependent Variable dan KELOMPOK dan PERLAKUAN ke kotak Fixed Factor(s), sehingga akan muncul tampilan berikut ini 7. Klik kotak Model, sehingga akan muncul tampilan sebagai berikut :
- 27. 199 8. Klik Custom, sehingga akan muncul tampilan sebagai berikut : 9. Masukkan KELOMPOK dan PERLAKUAN dengan mengklik tanda panah ko kotak Model, sehingga akan muncul tampilan berikut ini
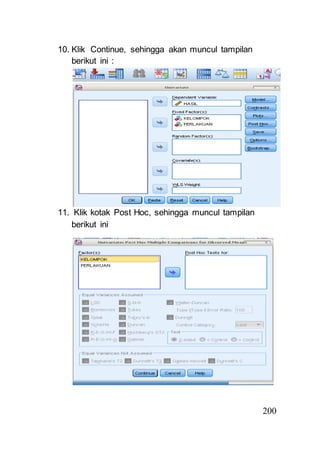
- 28. 200 10. Klik Continue, sehingga akan muncul tampilan berikut ini : 11. Klik kotak Post Hoc, sehingga muncul tampilan berikut ini
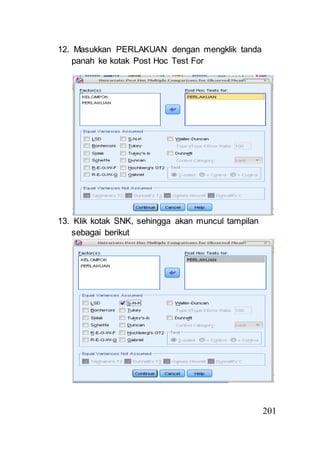
- 29. 201 12. Masukkan PERLAKUAN dengan mengklik tanda panah ke kotak Post Hoc Test For 13. Klik kotak SNK, sehingga akan muncul tampilan sebagai berikut
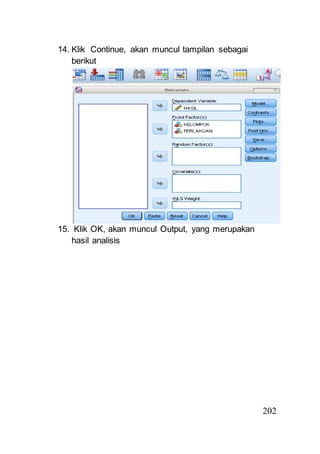
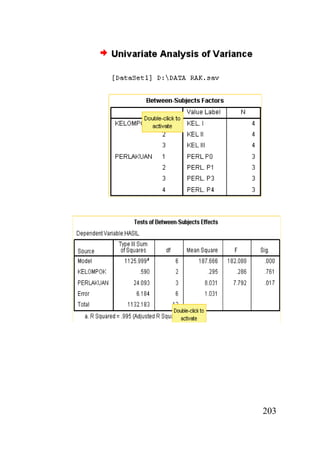
- 30. 202 14. Klik Continue, akan muncul tampilan sebagai berikut 15. Klik OK, akan muncul Output, yang merupakan hasil analisis
- 31. 203
- 32. 204