10.3 Chords and Segment Relationships
- 1. Chords and Segment Relationships The student is able to (I can): ŌĆó Apply properties of chords ŌĆó Find the lengths of segments formed by lines that intersect circles
- 2. In the same circle (or in congruent circles), two minor arcs are congruent if and only if their corresponding chords are congruent. E R O F m m FO RE FO RE ’üĆ ’üĆ
- 3. If a radius or diameter is perpendicular to a chord, then it bisects the chord and its arc. ER GO ŌŖź G E O R A GA AO ’üĆ GR RO ’üĆ
- 4. Example Find the length of . BU ŌĆó B L U E 2 5 x
- 5. Example Find the length of . BU ŌĆó B L U E 3 2 5 2 2 2 3 5 x + = x x = 4 BU = 2(4) = 8
- 6. If one chord of a circle is a perpendicular bisector of another chord, then the first chord is a diameter. The midpoint of the diameter would be the center of the circle. G W O N A If is a ŌŖź bisector of , then is a diameter. WN GO WN
- 7. A while back, I needed to find the center of a circle, so I used this property. Ōś║
- 8. A while back, I needed to find the center of a circle, so I used this property. Ōś║ Step 1: I drew a chord Step 2: I drew the perpendicular bisector, which is a diameter.
- 9. A while back, I needed to find the center of a circle, so I used this property. Ōś║ Step 3: I measured and found the midpoint of the diameter, which gave me the center!
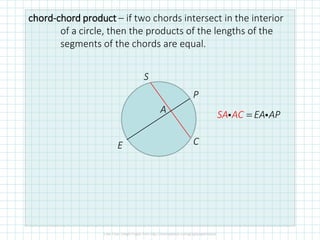
- 10. chord-chord product ŌĆō if two chords intersect in the interior of a circle, then the products of the lengths of the segments of the chords are equal. S P A C E P S E A AC A A =
- 11. Examples 1. Find the value of x. 2. What is the diameter of the circle? 9 12 x 6 ( ) 9 6 12 x = 9 72 x = 8 x = ( ) 4 6 6 x = 4 36 x = 9 x = diameter 4 9 13 = + = 6 6 4 x ŌĆó
- 12. secant-secant product ŌĆō if two secants intersect in the exterior of a circle, then the product of the lengths of one secant segment and its external segment equals the product of the lengths of the other secant segment and its external segment. (whole ŌĆó outside = whole ŌĆó outside) O P M E T M T O M EM M P =
- 13. Example Find the value of x. 10 x 8 12 ( ) ( ) 10 10 12 20 10 100 240 10 140 14 x x x x + = + = = =
- 14. secant-tangent product ŌĆō if a secant and a tangent intersect in the exterior of a circle, then the product of the lengths of the secant segment and its external segment equals the length of the tangent segment squared. (whole ŌĆó outside = tangent2) G O R F 2 FO RO GO =
- 15. Example Find the value of x. 8 10 x ( ) ( )( ) 2 2 2 10 8 8 18 8 144 12 x x x x + = = = =