データ解析13 线形判别分析
- 1. データ解析 第13回 2018年7月12日 八谷 大岳 1
- 3. 内容: 7 ? 判別分析とは ? 线形判别分析の基礎 ? 直線を用いたカテゴリ判別 ? カテゴリ間分散?カテゴリ内分散による定式化 ? 直線の最適化 ? 线形判别分析の応用 ? 手順 ? Pythonによる実装例
- 4. 回帰分析の復習 8 ? 回帰分析の目的:入力(説明変数)と出力(目的変数)の 関係を学習し、未知の入力に対する出力を予測する ? 目的変数:量的なデータ(連続値) ? 例:靴サイズ、ゴミの排出量、身長、株価、家賃など ??? = ??1 ??1 + ??2 ??2 + ??モデル式: 身長(x1) 体重(x2) 靴サイズ(y) 162 44 24.0 165 48 24.5 168 53 25.5 160 45 22.5 158 45 23.0 153 43 22.0 158 45 23.0 168 50 24.0 157 52 23.0 154 42 23.0 170 48 25.0 157 45 23.5 (cm) (kg) (cm) 説明変数??1 説明変数??2 目的変数?? 目的変数?? 靴サイズ=傾き X 身長 + 傾き X 体重 + 切片 + 残差 ??1 説明変数??1 説明変数??2??2 ?? ?? モデルパラメータ: ??1、??2(傾き)、??(??の切片)
- 5. 判別分析とは 9 ? 目的およびモデル式は回帰分析と同じ ? 入力(説明変数)と出力(目的変数)の関係を学習し、未知の入力に対する 出力を予測 ? ただし、目的変数が質的データ(カテゴリー)となっている ? 質的データの例:性別、勉強好き、合否 ? 判別分析の例:血圧と心拍数の値から病気か否かを判定したい 血圧 心拍数 病気 107 70 × 132 63 × 110 91 〇 160 85 〇 123 98 〇 ??? = ??1 ??1 + ??2 ??2 + ?? モデル式: ??? = 0.8??1 + 0.6??2 ? 150 判別分析により以下のモデル式が得られる ??? > 0の時「病気」であると判定 ??? ≤ 0の時「病気でない」であると判定 ???は連続値で、「0」を閾値としてカテゴリを判別
- 6. 演習1 10 1. 以下のデータ分析手法の概要について述べなさい。 2. 以下のモデル式が与えられた時、 入力「血圧??1 = 154」と 「心拍数??2 = 75」 が病気か否かを判別しなさい ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の一番上 に記載 分析手法 概要 回帰分析 判別分析 ??? = 0.8??1 + 0.6??2 ? 150 ??? > 0の時「病気」であると判定 ??? ≤ 0の時「病気でない」であると判定
- 7. 内容: 12 ? 判別分析とは ? 线形判别分析の基礎 ? 直線を用いたカテゴリ判別 ? カテゴリ間分散?カテゴリ内分散による定式化 ? 直線の最適化 ? 线形判别分析の応用 ? 手順 ? Pythonによる実装例
- 8. 线形判别分析の定式化 13 ? 学習データ: ? 入力(説明変数)??:実数値ベクトル ? 出力(目的変数)??:質的データ(カテゴリ) ? 主成分分析と同様に、データの平均??を通る直線??を考える ?????? = ????, ???? ??=1 ?? ?? ??1 ??2 教科書P142~ 直線??:??? = ??1 ??1 ? ??1 + ??2 ??2 ? ??2 =??Τ ?? ? ?? ???? = ??1 ?? , ??2 ?? Τ ????? モデルパラメータ?? = (??1, ??2)Τ: 正規基底ベクトル ?????は、各入力????を直線 ??に正射影した点 平均??: = ??1, ??2 Τ ?? ???? = ? 1 もし???? が??( × )に属す場合 ?1 もし???? が??(●)に属す場合
- 9. 演習2 14 ? モデルパラメータ:?? = 1, 1 Τ のとき、以下の問いに答えなさい。 1. 直線??のモデル式を書きなさい。 2. 直線??をグラフに描きなさい。 3. データ点??1 、??3 、??6 をモデル式に入力したときの出力 ?????を求め、 直線および平均との関係について考察しなさい。 4. 直線??がカテゴリP(●)とQ(×)を判別でるか考察しなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の一番上 に記載 6?? ??1 ??2 5 平均?? = 6,5 Τ ??3 = 5,9 Τ ??6 = 7,3 Τ ??1 = 3,4 Τ 直線??のモデル式: ??? = ??1 ??1 ? ??1 + ??2 ??2 ? ??2
- 10. 内容: 17 ? 判別分析とは ? 线形判别分析の基礎 ? 直線を用いたカテゴリ判別 ? カテゴリ間分散?カテゴリ内分散による定式化 ? 直線の最適化 ? 线形判别分析の応用 ? 手順 ? Pythonによる実装例
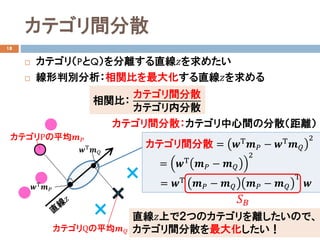
- 11. カテゴリ間分散 18 ? カテゴリ(PとQ)を分離する直線??を求めたい ? 线形判别分析:相関比を最大化する直線??を求める 相関比: カテゴリ間分散 カテゴリ内分散 カテゴリ間分散:カテゴリ中心間の分散(距離) カテゴリ間分散 = ??Τ ???? ? ??Τ ???? 2 = ??Τ ???? ? ???? 2 = ??Τ ???? ? ???? ???? ? ???? Τ ?? カテゴリPの平均???? 直線??上で2つのカテゴリを離したいので、 カテゴリ間分散を最大化したい! ???? カテゴリQの平均???? ??Τ ???? ??Τ ????
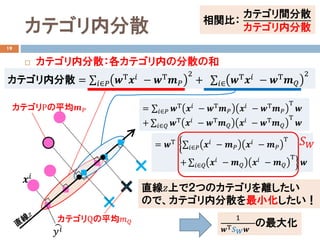
- 12. カテゴリ内分散 19 ? カテゴリ内分散:各カテゴリ内の分散の和 相関比: カテゴリ間分散 カテゴリ内分散 カテゴリPの平均???? ????? カテゴリ内分散 = ∑??∈?? ??Τ ???? ? ??Τ ???? 2 + ∑??∈ ??Τ ???? ? ??Τ ???? 2 = ∑??∈?? ??Τ ???? ? ??Τ ???? ???? ? ??Τ ???? Τ ?? + ∑??∈?? ??Τ ???? ? ??Τ ???? ???? ? ??Τ ???? Τ ?? = ??Τ ?∑??∈?? ???? ? ???? ???? ? ???? Τ ?+ ∑??∈?? ???? ? ???? ???? ? ???? Τ ?? ???? 直線??上で2つのカテゴリを離したい ので、カテゴリ内分散を最小化したい! ???? カテゴリQの平均???? 1 ??Τ ?? ?? ?? の最大化
- 13. 内容: 20 ? 判別分析とは ? 线形判别分析の基礎 ? 直線を用いたカテゴリ判別 ? カテゴリ間分散?カテゴリ内分散による定式化 ? 直線の最適化 ? 线形判别分析の応用 ? 手順 ? Pythonによる実装例
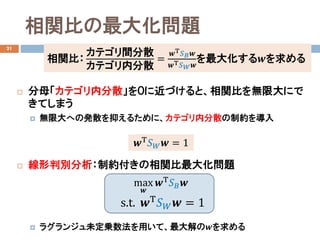
- 14. 相関比の最大化問題 21 ? 分母「カテゴリ内分散」を0に近づけると、相関比を無限大にで きてしまう ? 無限大への発散を抑えるために、カテゴリ内分散の制約を導入 ? 线形判别分析:制約付きの相関比最大化問題 ? ラグランジュ未定乗数法を用いて、最大解の??を求める max ?? ??Τ ???? ?? s.t. ??Τ ???? ?? = 1 ??Τ ???? ?? = 1 相関比: カテゴリ間分散 カテゴリ内分散 = ??Τ ???? ?? ??Τ ?? ?? ?? を最大化する??を求める
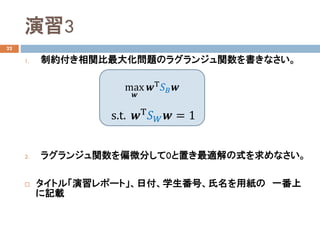
- 15. 演習3 22 1. 制約付き相関比最大化問題のラグランジュ関数を書きなさい。 2. ラグランジュ関数を偏微分して0と置き最適解の式を求めなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上 に記載 max ?? ??Τ ???? ?? s.t. ??Τ ???? ?? = 1
- 16. 内容: 24 ? 判別分析とは ? 线形判别分析の基礎 ? 直線を用いたカテゴリ判別 ? カテゴリ間分散?カテゴリ内分散による定式化 ? 直線の最適化 ? 线形判别分析の応用 ? 手順 ? Pythonによる実装例
- 17. 线形判别分析の手順 25 ? 以下の学習データに対して、线形判别分析を行う ? ステップ1:各カテゴリの平均を求める ??1 ??2 カテゴリ 3 4 P 4 5 P 5 9 P 9 5 Q 8 4 Q 7 3 Q 6?? ??1 ??2 5 平均値?? = 6,5 カテゴリPの平均???? = 1 3 3 4 + 4 5 + 5 9 = 1 3 12 18 = 4 6 カテゴリQの平均???? = 1 3 9 5 + 8 4 + 7 3 = 1 3 24 12 = 8 4
- 18. 线形判别分析手順2 26 ? ステップ2: 行列????、????および???? ?1 を求める ???? = ???? ? ???? ???? ? ???? Τ = 4 6 ? 8 4 4 6 ? 8 4 Τ = ?4 2 ?4 2 Τ = 16 ?8 ?8 4 ???? = 4 6 ???? = 8 4 ???? = ? ??∈?? ???? ? ???? ???? ? ???? Τ + ? ??∈?? ???? ? ???? ???? ? ???? Τ ??1 ??2 カテ ゴリ 3 4 P 4 5 P 5 9 P 9 5 Q 8 4 Q 7 3 Q = 3 4 ? 4 6 3 4 ? 4 6 Τ + 4 5 ? 4 6 4 5 ? 4 6 Τ + 5 9 ? 4 6 5 9 ? 4 6 Τ + 9 5 ? 8 4 9 5 ? 8 4 Τ + 8 4 ? 8 4 8 4 ? 8 4 Τ + 7 3 ? 7 3 8 4 ? 8 4 Τ = 1 2 2 4 + 0 0 0 1 + 1 3 3 9 + 1 1 1 1 + 0 0 0 0 + 1 1 1 1 = 4 7 7 16 ???? ?1 = 1 15 16 ?7 ?7 4
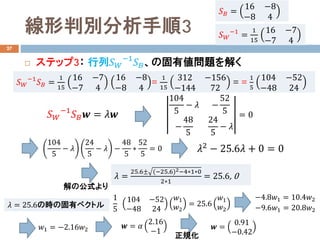
- 19. 线形判别分析手順3 27 ? ステップ3: 行列???? ?1 ????、の固有値問題を解く ???? = 16 ?8 ?8 4 ???? ?1 = 1 15 16 ?7 ?7 4 ???? ?1 ???? = 1 15 16 ?7 ?7 4 16 ?8 ?8 4 = 1 15 312 ?156 ?144 72 = = 1 5 104 ?52 ?48 24 ???? ?1 ???? ?? = ???? 104 5 ? ?? ? 52 5 ? 48 5 24 5 ? ?? = 0 104 5 ? ?? 24 5 ? ?? ? 48 5 ? 52 5 = 0 ?? = 25.6± (?25.6)2?4?1?0 2?1 = 25.6, 0 解の公式より ??2 ? 25.6?? + 0 = 0 ?? = 25.6の時の固有ベクトル 1 5 104 ?52 ?48 24 ??1 ??2 = 25.6 ??1 ??2 ?4.8??1 = 10.4??2 ?9.6??1 = 20.8??2 ??1 = ?2.16??2 ?? = ?? 2.16 ?1 ?? = 0.91 ?0.42正規化
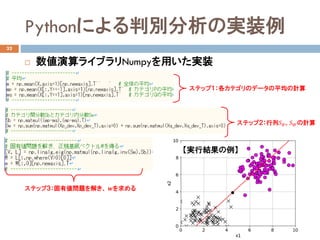
- 20. 线形判别分析手順4 28 ? ステップ4:求めた??を用いて、直線??のモデル式を作成 ? ステップ5:直線??をグラフに描き、学習データのカテゴリが 分離(判別)できることを確認 ? ステップ6:未知のデータのカテゴリを予測 直線??のモデル式: ??? = ??1 ??1 ? ??1 + ??2 ??2 ? ??2 = 0.91 ??1 ? 6 ? 0.42 ??2 ? 5 平均?? = 6,5 Τ ?? = 0.91 ?0.42
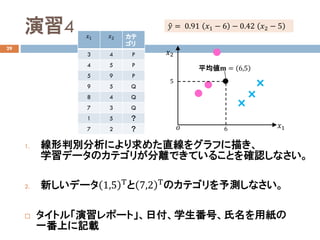
- 21. 演習4 29 1. 线形判别分析により求めた直線をグラフに描き、 学習データのカテゴリが分離できていることを確認しなさい。 2. 新しいデータ 1,5 Τと 7,2 Τのカテゴリを予測しなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 6?? ??1 ??2 5 平均値?? = 6,5 ??? = 0.91 ??1 ? 6 ? 0.42 ??2 ? 5 ??1 ??2 カテ ゴリ 3 4 P 4 5 P 5 9 P 9 5 Q 8 4 Q 7 3 Q 1 5 ? 7 2 ?
- 22. 内容: 31 ? 判別分析とは ? 线形判别分析の基礎 ? 直線を用いたカテゴリ判別 ? カテゴリ間分散?カテゴリ内分散による定式化 ? 直線の最適化 ? 线形判别分析の応用 ? 手順 ? Pythonによる実装例
- 24. 課題 33 ? 数学と英語の点数データに関する行列???? ?1 ???? = 0.83 0.4 0.68 0.32 、 平均?? = 4.2,3.8 Τのとき、线形判别分析を行いなさい。 1. 固有値問題を解き、直線??の正規基底ベクトル??を求めなさい。 2. 直線??のモデル式を書きなさい。 3. グラフに点数データと、求めた直線??および分類境界を描きなさい。 4. 直線??により、点数データのカテゴリが判別できるか否か考察しなさい。 5. 新しい学生の点数 0,8 Τ と 1,8 Τ を判別しなさい。 A B C D E F G H I J 数学??1 2 1 2 3 5 4 8 6 7 4 英語??2 3 4 2 2 4 4 5 3 6 5 カテゴリ P P P P Q Q Q Q Q Q 数学と英語の点数データ
- 25. レポートの提出方法 34 ? 演習レポート: ? タイトル「演習レポート」、日付?学生番号?氏名を用紙の一番上に記載 ? 課題レポート : ? タイトル「課題レポート」、出題日?学生番号?氏名を用紙の一番上に記載 ? 2ページ以上になる場合は、ホッチキス留め ? A4サイズの用紙を使用 ? 一度に複数の課題レポートを提出する場合出題日ごとに別々に綴じる