16 recommender systems
- 1. 16. Recommender Systems The movie prediction system simply try to predict the values of these missing values (with “?”) .. like what rating would the user have given to those films CONTENT BASED RECOMMENDER SYSTEM: x1 = degree to which a movie is a romantic movie x2 = degree to which a movie is an action movie n =2 = no of features, not counting the extra feature(x0→always =1)
- 2. X( 1 ) = feature values vector for movie 1 Θ( 1 ) = parameters vector learned for a particular user Procedure: Minimizing the sum over all i such that r(i, j) ==1
- 3. But we need to do this for all users: We get a separate parameter vector for each user, Θ( j ) Not all movies can be rated based on their content, or it’s just very difficult → so, collaborative learning comes to our rescue COLLABORATIVE FILTERING: feature learning → algo automatically learns what features to use If we have no idea how to rate a movie..
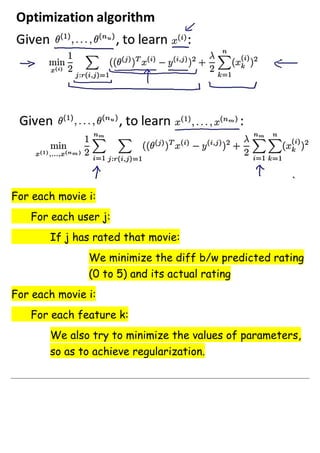
- 4. Let’s say, our users have told us the values of their own parameters Θ: We try to rate the movies automatically: We try to infer what should the vector X( 1 ) be so that:
- 5. For each movie i: For each user j: If j has rated that movie: We minimize the diff b/w predicted rating (0 to 5) and its actual rating For each movie i: For each feature k: We also try to minimize the values of parameters, so as to achieve regularization.
- 6. Diff b/w content based recommender vs Collaborative filtering: In content-based recommender: In collaborative filtering: So, what we can do to train the model is that: We can guess an initial Θ and obtain X from that Use that to obtain better fitting parameters (Θ) Use that to obtain better set of features (X) And so on … This actually works, as eventually this will converge to a reasonable set of features and a reasonable set of parameters for each user
- 7. ➢This algo is called collaborative filtering as each user is collaborating to advance the algo a little bit, i.e., they are helping the algo little bit Combining Collaborative filtering and content-based recommender: In content-based recommender: In collab. Featuring: Combing both: Here, if we keep X→ constant ➔ it’s minimized over Θ (content- based recommender) If we keep Θ → constant ➔ it’s minimized over X (collaborative filtering)
- 8. Here: we don’t need x0 =1 and also don’t need Θ0 ➔ because since our algo is learning its own features, we don’t need to hardcode any features, it will learn x1==1 by itself (since we don’t give x0) Procedure: VECTORIZATION:LOW RANK FACTORIZATION ALGORITHM:
- 9. We can create an X vector which contains features of all examples row-wise And we can also create a Θ vector which contains parameters of all examples row-wise So, we can obtain the predicted rating matrix as: This is a low rank matrix (→ a property of linear algebra) Application:
- 10. MEAN NORMALIZATION: In such case, the last regularization term will give a 0 vector for Θ( 5 ) (parameter vector for Eve). This will cause all predicted ratings of Eve to be 0. But that’s not useful, as all the movies will be equally likely for Eve Mean Normalization: it can be used as a data pre-processing step: First, we find the mean rating of each movie by different users
- 11. Then we Subtract the mean from each user’s ratings Now, we use this matrix to learn our parameters for each user and feature-values of each movie. Also, we add the calculated mean to our predicted ratings at the end of prediction
- 12. This way we have: So, the user who has not rated any movie will get an average rating for each movie. ‚û¢Mean normalization can also be used in case when a movie has no rating from any user, by modifying the algo a little bit.