![0/1 Knapsack
? DP ??
¨C ??[?][?] : 1 ~ i? ??? ???? ??? ?? j? ??
? ???? ? ??? ???
¨C ??[0][0] = 0, ??[0][?] = ?¡Þ ( 0 < ? <= ? )
¨C ??[?][?] =
9
??[? ¨C 1][?] ( ? < ? ? )
max ( ??[? ¨C 1][?], ??[? ¨C 1][? ¨C ?[?]] + ?[?]) ( ? >= ?[?] )
????? : O(??) ????? : O(??)](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-9-320.jpg)
![0/1 Knapsack
ii - 1
??[?][?]??[? ¨C 1][?]
??[? ¨C 1][? ¨C ??]](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-12-320.jpg)
![Unbounded Knapsack
? ??[?][?] : 1 ~ ?? ??? ???? ?? ??
?? ??? ???? ? ?? ??
? ??[0][0] = 0, ??[0][?] = ?¡Þ (0 < ? <= ?)
? ??[?][?] = max ( ??[? ¨C 1][? ¨C ? ? ??] +
? ? ??) (? >= 0)
????? O(??K
)
?? ?? ?? ????](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-18-320.jpg)
![Unbounded Knapsack
? ??[?][?]
= max ?? ? ¨C 1 ? ¨C ? ? ?? + ? ? ??
(? ¡Ý 0)
= max( ?? ? ¨C 1 ? , max( ?? ? ¨C 1 ? ¨C ? ? ??
+ ? ? ??)) (? ¡Ý 1)
= max( ?? ? ¨C 1 ? , max( ?? ? ¨C ? ? ¨C ?? ¨C ? ? ??
+ ? ? ??) + ??) (? ¡Ý 0)
= max ( ??[? ¨C 1][?], ??[?][? ¨C ??] + ??)](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-19-320.jpg)
![Unbounded Knapsack
? ??[? ¨C 1][? ¨C ??] => ??[?][? ¨C ??]](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-20-320.jpg)
![Bounded Knapsack
? ?? = 2
+ 2]
+ 2K
+ ¡ + 2^
+ ?
(0 ¡Ü ? < 2^`]
)
? ??, ??, ??
? ????? O(nWlogm)
? ?? ? 2
, ?? ? 2
, 1 , ¡ , ?? ? ?, ?? ? ?, 1
? 0/1 Knapsack](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-25-320.jpg)
![Bounded Knapsack
? ?? dp?? ???
? ??[?][?] = max ( ??[? ¨C 1][? ¨C ? ? ??] +
? ? ??) (0 <= ? <= ??)
? ?? ?? O(???)
? ????? k? ????.](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-27-320.jpg)
![Bounded Knapsack
? ? = ?? ? ? + ? (0 ¡Ü r < wi), ?? ? ??
? ??[?][?]
? ?? ?? ? => ? ? ?? ?? ?
= max ?? ? ? 1 ? ? ? ? ?? + ? ? ?? (0 ¡Ü ? ¡Ü ??)
= max ?? ? ? 1 ? ? ? ? ?? + ? + ? ? ??
= max ?? ? ? 1 ? ? ? ? ?? + ? ? ? ? ? ? ?? + ? ? ??](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-29-320.jpg)
![Bounded Knapsack
? ? ? ? = ?
? ?(?) = ??[? ? 1][? ? ?? + ?] ? ? ? ??
? ?? [? ? ??, ?]?? f(x)? ??? ?? ???
??
? RMQ? ?? O(logm)???
? ?(deque)? ???? O(1)? ??
?? ? ? = max ?? ? ? 1 ? ? ?? + ? ? ? ? ?? + ? ? ??
(q ? mi ¡Ü x ¡Ü q)
? ????? O(nW)](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-30-320.jpg)
![Tree DP
v
w1 w2 wn. . .
dp[v]
dp[w1] dp[w2] dp[wn]](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-36-320.jpg)
![Tree DP
v1 . . .
dp[v1]
vm
dp[vm]
Root
.
.
.
.
.
.
.
.
.
dp[root]](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-37-320.jpg)
![Tree DP
v1 . . .
dp[v1][a1]
vm
dp[vm][a1]
Root
.
.
.
.
.
.
.
.
.
dp[root][a1]](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-38-320.jpg)
![Tree DP
v1 . . .
dp[v1][a1]..[an]
vm
dp[vm][a1]..[an]
Root
.
.
.
.
.
.
.
.
dp[root][a1]..[an]](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-39-320.jpg)
![??? ????(BOJ 2213)
? dp[u][c] : u? ??? ?? ???? u?
????(c = 1) ?? ???? ???(c =
0) ?? ?? ??? ??
? ?? ? 1 = ¡Æ ?? ? 0
? ??[?][0] = ¡Æ max ?? ? 0 , ?? ? 1
(v? c? ?? ??)
? ??[????][0] = 0, ??[????][1] = 1](https://image.slidesharecdn.com/1-ddpknapsacktreedp-170828020008/85/1-D-Knapsack-Tree-DP-43-320.jpg)
???? ???? ??? 1-D (Knapsack, Tree DP)
- 2. ?? ?? ? Knapsack ? Tree DP
- 4. Knapsack Problem ?? : Wikipedia
- 5. Knapsack Problem? ?? ? Fractional Knapsack ¨C ??? ?? ? ?? ? 0/1 Knapsack ¨C ??? ?? ? ?? ¨C Unbounded Knapsack (??? ??? ??) ¨C Bounded Knapsack (??? ??? ??)
- 6. Fractional Knapsack ? ??? ????, ?? ??? ??? ?? ? ? ??? ?? ??. ??? ?? ??? ? ?? ??? ?? ?? ??. ?? ?? ? ??? ? ?, ?? ?? ?????
- 7. Fractional Knapsack ? Greedy ?? ¨C ?? / ??? ? ??? ??? ?????. ¨C ?? ???? ??? ?????. ? ????? O(?????)
- 9. 0/1 Knapsack ? DP ?? ¨C ??[?][?] : 1 ~ i? ??? ???? ??? ?? j? ?? ? ???? ? ??? ??? ¨C ??[0][0] = 0, ??[0][?] = ?¡Þ ( 0 < ? <= ? ) ¨C ??[?][?] = 9 ??[? ¨C 1][?] ( ? < ? ? ) max ( ??[? ¨C 1][?], ??[? ¨C 1][? ¨C ?[?]] + ?[?]) ( ? >= ?[?] ) ????? : O(??) ????? : O(??)
- 10. 0/1 Knapsack
- 11. 0/1 Knapsack ? ???? ??(Sliding window) ?? ¨C ? ?? ?? swapping?? ?????? ? ?? ?? ¨C ?? => 2?? ??? ??
- 12. 0/1 Knapsack ii - 1 ??[?][?]??[? ¨C 1][?] ??[? ¨C 1][? ¨C ??]
- 13. 0/1 Knapsack ? ?? ? => ? % 2, ?? ? => 1 ¨C ? % 2
- 14. 0/1 Knapsack ? 2? => ?? ??? ??! ii - 1 j ii - 1 j j ?? ??
- 15. 0/1 Knapsack
- 16. 0/1 Knapsack ? ??? ?? 1, 2, ¡ , ???? ??? 0? ? ?? ??? ????? ??
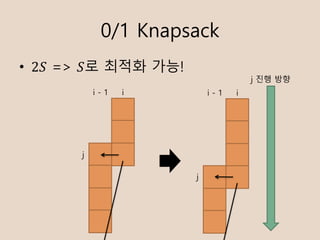
- 17. Unbounded Knapsack ? ??? ??? ?? ??? ??? ??? ?? ? ??. ??? ??? ?? ???? ? ?? ??? ???? ?, ?? ??? ? ??? ???. (?, ?? ??? ??? ? ??? ??? ?? ????) ? 1 <= ? <= 1000 ? 1 <= ??, ?? <= 1000 ? 1 <= ? <= 10000
- 18. Unbounded Knapsack ? ??[?][?] : 1 ~ ?? ??? ???? ?? ?? ?? ??? ???? ? ?? ?? ? ??[0][0] = 0, ??[0][?] = ?¡Þ (0 < ? <= ?) ? ??[?][?] = max ( ??[? ¨C 1][? ¨C ? ? ??] + ? ? ??) (? >= 0) ????? O(??K ) ?? ?? ?? ????
- 19. Unbounded Knapsack ? ??[?][?] = max ?? ? ¨C 1 ? ¨C ? ? ?? + ? ? ?? (? ¡Ý 0) = max( ?? ? ¨C 1 ? , max( ?? ? ¨C 1 ? ¨C ? ? ?? + ? ? ??)) (? ¡Ý 1) = max( ?? ? ¨C 1 ? , max( ?? ? ¨C ? ? ¨C ?? ¨C ? ? ?? + ? ? ??) + ??) (? ¡Ý 0) = max ( ??[? ¨C 1][?], ??[?][? ¨C ??] + ??)
- 20. Unbounded Knapsack ? ??[? ¨C 1][? ¨C ??] => ??[?][? ¨C ??]
- 23. Bounded Knapsack ? ??? ??, ??? ?? ??, ??, ??? ?? ? ??? ??. ??? ??? ?? ?? ?? ??? ??? ???? ?, ?? ? ?? ???? ???. ? 1 ¡Ü ? ¡Ü 1000 ? 1 ¡Ü ??, ?? ¡Ü 1000 ? 1 ¡Ü ?? ¡Ü 1000 ? 1 ¡Ü ? ¡Ü 10000
- 24. Bounded Knapsack ? (??, ??, ??) => ???? (??, ??, 1)? ?? => 0/1 Knapsack ? ????? O(W ¡Æ ??) => TLE
- 25. Bounded Knapsack ? ?? = 2 + 2] + 2K + ¡ + 2^ + ? (0 ¡Ü ? < 2^`] ) ? ??, ??, ?? ? ????? O(nWlogm) ? ?? ? 2 , ?? ? 2 , 1 , ¡ , ?? ? ?, ?? ? ?, 1 ? 0/1 Knapsack
- 26. Bounded Knapsack
- 27. Bounded Knapsack ? ?? dp?? ??? ? ??[?][?] = max ( ??[? ¨C 1][? ¨C ? ? ??] + ? ? ??) (0 <= ? <= ??) ? ?? ?? O(???) ? ????? k? ????.
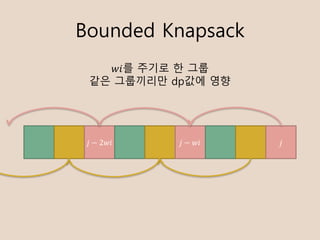
- 28. Bounded Knapsack ?? ? ??? ? 2?? ??? ??? ? ?? ?? ????? dp?? ??
- 29. Bounded Knapsack ? ? = ?? ? ? + ? (0 ¡Ü r < wi), ?? ? ?? ? ??[?][?] ? ?? ?? ? => ? ? ?? ?? ? = max ?? ? ? 1 ? ? ? ? ?? + ? ? ?? (0 ¡Ü ? ¡Ü ??) = max ?? ? ? 1 ? ? ? ? ?? + ? + ? ? ?? = max ?? ? ? 1 ? ? ? ? ?? + ? ? ? ? ? ? ?? + ? ? ??
- 30. Bounded Knapsack ? ? ? ? = ? ? ?(?) = ??[? ? 1][? ? ?? + ?] ? ? ? ?? ? ?? [? ? ??, ?]?? f(x)? ??? ?? ??? ?? ? RMQ? ?? O(logm)??? ? ?(deque)? ???? O(1)? ?? ?? ? ? = max ?? ? ? 1 ? ? ?? + ? ? ? ? ?? + ? ? ?? (q ? mi ¡Ü x ¡Ü q) ? ????? O(nW)
- 31. Bounded Knapsack
- 32. Knapsack ??? ? ??/?? ??? ??? ?/?? ?? ? ??? ?? ?? ?? ? ?, ?, ? ? ??? ??? ?? dp?? ?? ? ?? ¨C ?? ?? ?? ?, ?? ?? ? ?? dp? ?? => meet in the middle ? ? ??? ??? ?? ?? / ??? ?? ???
- 33. Knapsack ?? ??? ? ?(BOJ 7579) ? ??1(BOJ 2293) ? ??2(BOJ 2294) ? ??(BOJ 1226) ? Buying Apples!(SPOJ ABA12C) ? Large Knapsack(SPOJ LKS)
- 34. Tree DP
- 35. Tree DP ?? ? ?? ???? ?? ?? ???? ?? ????? ?? ??? ? ? ?? ?? = ?? ??
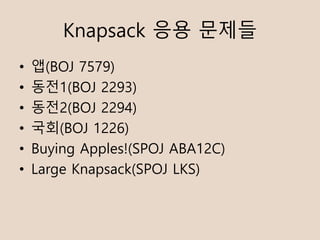
- 36. Tree DP v w1 w2 wn. . . dp[v] dp[w1] dp[w2] dp[wn]
- 37. Tree DP v1 . . . dp[v1] vm dp[vm] Root . . . . . . . . . dp[root]
- 38. Tree DP v1 . . . dp[v1][a1] vm dp[vm][a1] Root . . . . . . . . . dp[root][a1]
- 39. Tree DP v1 . . . dp[v1][a1]..[an] vm dp[vm][a1]..[an] Root . . . . . . . . dp[root][a1]..[an]
- 40. Tree DP? ?? ?? ? ??? DP ?? ????. ? ?? ??? DP?? ?? ??? DP? ? ?? ??? ???. ? ? ????? DP?? ????.(base) ? ??? ??.
- 41. Tree DP ?? ???? ? ??? ????(??? ??? ???) ???? ?? ? ???? ????? NP? ?? ¨C Ex) ?? ?? ??
- 42. ??? ????(BOJ 2213) ? ?? ?? ??(maximum independent set) ???, ???? ????? NP ? ???? ??? ?? DP? ?? ??? ?? ??
- 43. ??? ????(BOJ 2213) ? dp[u][c] : u? ??? ?? ???? u? ????(c = 1) ?? ???? ???(c = 0) ?? ?? ??? ?? ? ?? ? 1 = ¡Æ ?? ? 0 ? ??[?][0] = ¡Æ max ?? ? 0 , ?? ? 1 (v? c? ?? ??) ? ??[????][0] = 0, ??[????][1] = 1
- 44. ?? ??? ??(AOJ GALLERY) ? ??? ?? ? ?? ?? ??(minimum dominating set) ??? ??, ????? ???? ??? ?? NP ? ???? ?? ??? ?? ? ??? DP ???? ???? ?? ??
- 45. ? ? Tree DP ??? ? ??? ???(BOJ 2533) ¨C ?? ??? ?? ??? ?? ? ?? ???(BOJ 2337) ? ????(BOJ 1805) ? ?? ??(BOJ 2454) ? ????(BOJ 2584) ? ??? ???(BOJ 1289) ? ?? ????(BOJ 1693) ? Karen and Supermarket(CF 815C) ? An overnight dance in discotheque(CF 814D)
- 46. Reference ? ???? ?? ?? ?? ? ????? ???? ??? ? http://codedoc.tistory.com/18
- 47. ?????!