1-D Steady Heat conduction FDM
- 1. www.engineeringwithsandeep.com| Student Assignment Assignment No. 07 1-D Steady Heat conduction FDM 14.04.2021 Shivam Choubey Student No: CFDB30321004
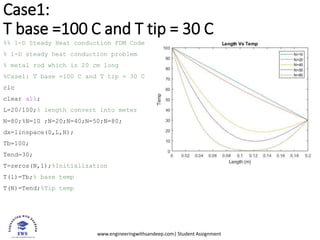
- 2. www.engineeringwithsandeep.com| Student Assignment Case1: T base =100 C and T tip = 30 C %% 1-D Steady Heat conduction FDM Code % 1-D steady heat conduction problem % metal rod which is 20 cm long %Case1: T base =100 C and T tip = 30 C clc clear all; L=20/100;% length convert into meter N=80;%N=10 ;N=20;N=40;N=50;N=80; dx=linspace(0,L,N); Tb=100; Tend=30; T=zeros(N,1);%Initialization T(1)=Tb;% base temp T(N)=Tend;%Tip temp
- 3. www.engineeringwithsandeep.com| Student Assignment k=100;% Correction loop for j=1:k for i=2:N-1 T(i)=(T(i+1)+T(i-1))/2; end T(N)=Tend;%Tip temp end plot(dx,T); hold on xlabel("Length (m)") ylabel("Temp") title("Length Vs Temp") legend("N=10","N=20","N=40","N=50","N=80") hold on
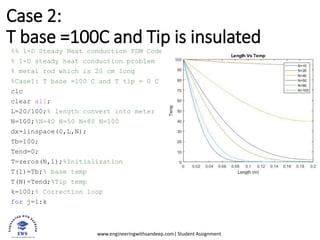
- 4. www.engineeringwithsandeep.com| Student Assignment Case 2: T base =100C and Tip is insulated %% 1-D Steady Heat conduction FDM Code % 1-D steady heat conduction problem % metal rod which is 20 cm long %Case1: T base =100 C and T tip = 0 C clc clear all; L=20/100;% length convert into meter N=100;%N=40 N=50 N=80 N=100 dx=linspace(0,L,N); Tb=100; Tend=0; T=zeros(N,1);%Initialization T(1)=Tb;% base temp T(N)=Tend;%Tip temp k=100;% Correction loop for j=1:k
- 5. www.engineeringwithsandeep.com| Student Assignment for i=2:N-1 T(i)=(T(i+1)+T(i-1))/2; end %T(N)=Tend;%Tip temp T(N)=T(N-1);%condition for insulated tip end plot(dx,T); hold on xlabel("Length (m)") ylabel("Temp") title("Length Vs Temp") legend("N=10","N=20","N=40","N=50","N=80","N=100") hold on