2 1 ЮКЮЛЮЌЯЮМЮБЯЮБ
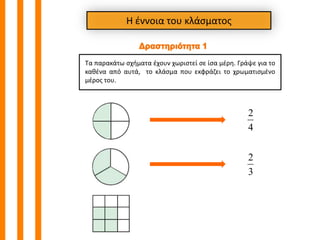
- 2. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ .
- 3. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 2 4
- 4. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 2 4
- 5. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 2 4 2 3
- 6. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 2 4 2 3
- 7. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 2 4 2 3 4 9
- 8. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ .
- 9. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 6 8
- 10. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 6 8
- 11. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 6 8 1 3
- 12. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 6 8 1 3
- 13. Ю ЮЖЮНЮНЮПЮЙЮБ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮЄЮБ ЯЮБЯЮБЮКЮЌЯЯ ЯЯЮЙЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮЏЯЮБ ЮМЮЖЯЮИ. ЮЯЮЌЯЮЕ ЮГЮЙЮБ ЯЮП ЮКЮБЮКЮЖЮНЮБ ЮБЯЯ ЮБЯ ЯЮЌ, ЯЮП ЮКЮЛЮЌЯЮМЮБ ЯЮПЯ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЯЮП ЯЯЯЮМЮБЯЮЙЯЮМЮЖЮНЮП ЮМЮЖЯЮПЯ ЯЮПЯ . 6 8 1 3 25 40
- 14. ЮЯЮЙЯЮМЯЯ ЮЮЌЮКЮЕ ЮКЮЛЮЌЯЮМЮБ ЮЕЮКЯЯЮЌЮЗЮЕЮЙ ЮЖЮНЮБ ЮМЮЖЯЮПЯ ЮЕЮНЯЯ ЮМЮЕЮГЮЖЮКЮПЯ Я. Я.Я. ЮЄЮП ЮКЮЛЮЌЯЮМЮБ ЮК ЮДЮЕЮЏЯЮНЮЕЮЙ ЯЯЮЙ ЮМЮЙЮБ ЯЮПЯЯЯЮИЯЮБ ЮЖЯЮЕЮЙ ЯЯЯЮЙЯЯЮЕЮЏ ЯЮЕ ЮН ЮЏЯЮБ ЮМЮЖЯЮИ ЮБЯЯ ЮН ЯЮБ ЮПЯЮПЮЏЮБ ЮЕЮМЮЕЮЏЯ ЮЖЯЮПЯ ЮМЮЕ ЮЕЯЮЙЮЛЮЖЮОЮЕЮЙ ЯЮБ ЮК .
- 15. ЮЄЮБ ЮМЮЖЯЮИ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮБЯЮЙЮКЮМЮИЯЮЙЯ ЮК ЮН ЯЮБЯЮПЮНЮПЮМЮБЯЯЮЙЯ Ю ЮЁЮЮЂЮЮЇЮ: Ю ЯЮБЯЮПЮНЮПЮМЮБЯЯЮЙЯ ЮЕЮНЯЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮДЮЕЮН ЮЕЮЏЮНЮБЮЙ ЯЮПЯЮЖ 0. ЮЮЌЮКЮЕ ЮКЮЛЮЌЯЮМЮБ ЯЮБЯЮЙЯЯЮЌЮНЮЕЮЙ ЮКЮБЮЙ ЯЮП ЯЮИЮЛЮЏЮКЮП ЯЮИЯ ЮДЮЙЮБЮЏЯЮЕЯЮИЯ ЯЮПЯ ЮБЯЮЙЮКЮМЮИЯЮЙ ЮДЮЙЮЌ ЯЮПЯ ЯЮБЯЮПЮНЮПЮМЮБЯЯЮЙ.
- 16. ЮЯЮПЮДЯЮНЮБЮМЮБ ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЯЮП ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЛЮЖЮГЮПЮНЯЮБЮЙ ЮЙЯЮПЮДЯЮНЮБЮМЮБ ЮЙ ЮЏЯЮБ ЯЯЮБЮН ЮЕЮКЯЯЮЌЮЗЮПЯ ЮН ЯЮП ЮЏЮДЮЙЮП ЮМЮЖЯЮПЯ ЮЕЮНЯЯ ЮМЮЕЮГЮЖЮКЮПЯ Я ЮЙ ЮЏЯЯЮН ЮМЮЕЮГЮЕЮКЯЮН. ЮЯЮЕЮЙЮДЮЙ ЮБЮКЯЮЙЮВЯЯ ЮЕЮКЯЯЮЌЮЗЮПЯ ЮН ЯЮП ЮЏЮДЮЙЮП ЮМЮЖЯЮПЯ ЮЕЮНЯЯ ЮМЮЕЮГЮЖЮКЮПЯ Я ЮЕЮЏЮНЮБЮЙ ЮКЮБЮЙ ЮЏЯЮБ ЮКЮБЮЙ ЮГЯЮЌЯЮПЯ ЮМЮЕ: ЮБ ЮВ ЮГ ЮД
- 17. ЮЯЮПЮДЯЮНЮБЮМЮБ ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЯЮП ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЛЮЖЮГЮПЮНЯЮБЮЙ ЮЙЯЮПЮДЯЮНЮБЮМЮБ ЮЙ ЮЏЯЮБ ЯЯЮБЮН ЮЕЮКЯЯЮЌЮЗЮПЯ ЮН ЯЮП ЮЏЮДЮЙЮП ЮМЮЖЯЮПЯ ЮЕЮНЯЯ ЮМЮЕЮГЮЖЮКЮПЯ Я ЮЙ ЮЏЯЯЮН ЮМЮЕЮГЮЕЮКЯЮН. ЮЯЮЕЮЙЮДЮЙ ЮБЮКЯЮЙЮВЯЯ ЮЕЮКЯЯЮЌЮЗЮПЯ ЮН ЯЮП ЮЏЮДЮЙЮП ЮМЮЖЯЮПЯ ЮЕЮНЯЯ ЮМЮЕЮГЮЖЮКЮПЯ Я ЮЕЮЏЮНЮБЮЙ ЮКЮБЮЙ ЮЏЯЮБ ЮКЮБЮЙ ЮГЯЮЌЯЮПЯ ЮМЮЕ: ЮБ ЮВ = ЮГ ЮД = =
- 18. =
- 19. = = =
- 21. Ю ЯЯ ЮДЮИЮМЮЙЮПЯ ЯЮГЮПЯЮМЮЕ ЮЙЯЮПЮДЯЮНЮБЮМЮБ ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЮЙЮБ ЮНЮБ ЮКЮБЯЮБЯЮКЮЕЯ ЮЌЯЮПЯ ЮМЮЕ ЮЙЯЮПЮДЯЮНЮБЮМЮБ ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЙ ЮГЮЙЮБ ЮНЮБ ЮДЮЙЮБЯЮЙЯЯЯЯЮПЯ ЮМЮЕ ЯЯЮЙ ЮДЯЮП ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЕЮЏЮНЮБЮЙ ЮЙЯЮПЮДЯЮНЮБЮМЮБ, ЮМЯЮПЯЮПЯЮМЮЕ ЮНЮБ ЮЕЯЮБЯЮМЯЮЗЮПЯ ЮМЮЕ ЯЮПЯ Я ЯЮБЯЮБЮКЮЌЯЯ ЮКЮБЮНЯЮНЮЕЯ: ЮЯЮБЮН ЯЮПЮЛЮЛЮБЯЮЛЮБЯЮЙЮБЯЯЮПЯЮН ЮПЮЙ ЯЯЮПЮЙ ЮЕЮНЯЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮМЮЕ ЯЮПЮН ЮЏЮДЮЙЮП ЯЯ ЯЮЙЮКЯ ЮБЯЮЙЮКЮМЯ (т 0) ЯЯЮПЮКЯЯЯЮЕЮЙ ЮКЮЛЮЌЯЮМЮБ ЮЙЯЮПЮДЯЮНЮБЮМЮП. ЮЯЮБЮН ЮДЮЙЮБЮЙЯЮЕЮКЮПЯЮН ЮПЮЙ ЯЯЮПЮЙ ЮЕЮНЯЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮМЮЕ ЯЮПЮН ЮЏЮДЮЙЮП ЯЯ ЯЮЙЮКЯ ЮБЯЮЙЮКЮМЯ (т 0) ЯЯЮПЮКЯЯЯЮЕЮЙ ЮКЮЛЮЌЯЮМЮБ ЮЙЯЮПЮДЯЮНЮБЮМЮП. Я.Я 3 5 3 4 5 4 12 20 20 25 20 : 5 25 : 5 4 5 Ю ЮДЮЙЮБЮДЮЙЮКЮБЯЮЏЮБ ЮМЮЕ ЯЮИЮН ЮПЯЮПЮЏЮБ ЯЯЮПЮКЯЯЯЮЕЮЙ ЮЙЯЮПЮДЯЮНЮБЮМЮП ЮКЮЛЮЌЯЮМЮБ ЮЖЯЮЕЮЙЯЮБ ЮБЯЯ ЮДЮЙЮБЮЏЯЮЕЯЮИ ЯЯЮН ЯЯЯЮН ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮМЮЕ ЯЮПЮН ЮЏЮДЮЙЮП ЯЯ ЯЮЙЮКЯ ЮБЯЮЙЮКЮМЯ, ЮЛЮЖЮГЮЕЯЮБЮЙ ЮБЯЮЛЮПЯЮПЮЏЮЗЯЮЗ ЯЮПЯ ЮКЮЛЮЌЯЮМЮБЯЮПЯ ЮКЮБЮЙ ЮЖЯЮЕЮЙ ЯЯ ЮБЯЮПЯЮЖЮЛЮЕЯЮМЮБ ЮЖЮНЮБ ЮКЮЛЮЌЯЮМЮБ ЮЙЯЮПЮДЯЮНЮБЮМЮП ЮМЮЕ ЯЮП ЮБЯЯЮЙЮКЯ ЮМЮЕ ЮМЮЙЮКЯЯЯЮЕЯЮПЯ Я ЯЯЮПЯ Я. ЮЄЮП ЮКЮЛЮЌЯЮМЮБ ЮЕЮКЮЕЮЏЮНЮП ЯЮПЯ ЮДЮЕЮН ЮМЯЮПЯЮЕЮЏ ЮНЮБ ЮБЯЮЛЮПЯЮПЮЙЮИЮКЮЕЮЏ (ЮДЮЕЮН Я ЯЮЌЯЯЮЕЮЙ ЮЌЮЛЮЛЮПЯ ЮКЮПЮЙЮНЯЯ ЮДЮЙЮБЮЙЯЮЖЯЮИЯ ЮБЯЮЙЮКЮМЮИЯЮЙ ЮКЮБЮЙ ЯЮБЯЮПЮНЮПЮМЮБЯЯЮЙ ЮЕЮКЯЯЯ ЮБЯЯ ЯЮИ ЮМЮПЮНЮЌЮДЮБ) ЮЛЮЖЮГЮЕЯЮБЮЙ ЮБЮНЮЌЮГЯЮГЮП.
- 22. ЮЮМЯЮНЯ ЮМЮБ - ЮЯЮЕЯЯЮНЯ ЮМЮБ ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЯЮБЮН ЮДЯЮП ЮЙ ЯЮЕЯЮЙЯЯЯЯЮЕЯЮБ ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЖЯЮПЯ ЮН ЯЮПЮН ЮЏЮДЮЙЮП ЯЮБЯЮПЮНЮПЮМЮБЯЯЮЙ ЮЛЮЖЮГЮПЮНЯЮБЮЙ ЮПЮМЯЮНЯ ЮМЮБ ЮКЮБЮЙ ЯЯЮБЮН ЮЖЯЮПЯ ЮН ЮДЮЙЮБЯЮПЯЮЕЯЮЙЮКЮПЯЯ ЯЮБЯЮПЮНЮПЮМЮБЯЯЮЖЯ ЮПЮНЮПЮМЮЌЮЗЮПЮНЯЮБЮЙ ЮЕЯЮЕЯЯЮНЯ ЮМЮБ. Я.Я 3 12 , 5 5 2 7 , 3 8 ЮПЮМЯЮНЯ ЮМЮБ ЮКЮЛЮЌЯЮМЮБЯЮБ ЮЕЯЮЕЯЯЮНЯ ЮМЮБ ЮКЮЛЮЌЯЮМЮБЯЮБ
- 23. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 24. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 25. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 26. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 27. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 28. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 29. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 30. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 31. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 32. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 33. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я
- 34. ЮЯЯЯЮЙЯЮЕЮЙЯ ЮЃЯЯЯЮПЯ - ТьЮЌЮКЮПЯ Я