2019 ي™چىµëŒ€ي•™êµگ ي”„ë،œê·¸ëکë°چ ê²½ى§„대يڑŒ ي’€ى´ ىٹ¬ë¼ى´ë“œ (Open Contestىڑ©)
- 1. 2019 ي™چىµëŒ€ي•™êµگ ي”„ë،œê·¸ëکë°چ ê²½ى§„대يڑŒ ي’€ى´ 2019.11.01
- 2. A ë‚کىک ي•™ى گى€ ى œى¶œ : 136يڑŒ ى •ë‹µ : 71ëھ… (ى •ë‹µë¥ 52%) First Solve : ê¹€Xىڑ±ë‹ک (3분) ى¶œى œىگ : wonjaek36
- 3. A ë‚کىک ي•™ى گى€? int score[51], my_score; for(int i=1; i<=50; ++i) scanf(“%dâ€, &score[i]); scanf(“%dâ€, &my_score); for(int i=1; i<=50; ++i){ if(score[i] == my_score){ //i등ى—گ ي•´ë‹¹ي•کëٹ” //ي•™ى گى„ ى¶œë ¥ } } ى´ëں° ى‹¤ىˆک들ى´ ىˆى—ˆىٹµë‹ˆë‹¤ : - ى¸ëچ±ىٹ¤ë¥¼ 0~49ë،œ ى،ى•کëٹ”ëچ°, 등ىˆکëٹ” 1~50 ىœ¼ë،œ ي™•ى¸ي•œë‹¤. - score[]ى•ˆى—گ ë‚´ 등ىˆکê°€ ى—†ë‹¤ê³ ىƒê°پي•کê³ , ë°°ى—´ ë‚´ى—گى„œ ê°™ى€ ى گىˆکىک 등ىˆک를 ى°¾ى§€ ى•ٹëٹ” 다.
- 4. B ê³µى£¼ë‹کى„ 구ي•´ë¼! ى œى¶œ : 206يڑŒ ى •ë‹µ : 11ëھ… (ى •ë‹µë¥ 5%) First Solve : ê¹€Xىڑ±ë‹ک (17분) ى¶œى œىگ : wonjaek36
- 5. B ê³µى£¼ë‹کى„ 구ي•´ë¼! ê·¸ëŒى„ ى–»ى—ˆىœ¼ë©´ ë²½ى„ 무ى‹œي•ک므ë،œ, ê³µى£¼ë‹ک까ى§€ 다ى´ë ‰يٹ¸ë،œ ê°ˆ ىˆک ىˆىٹµë‹ˆë‹¤. BFS를 ى´ىڑ©ي•´ى„œ, â‘ ê·¸ëŒê¹Œى§€ىک 거리, â‘،ê³µى£¼ë‹ک까ى§€ىک 거리를 구ي•کë©´ ىµœë‹¨ê±°ë¦¬ëٹ” min(â‘ +ê·¸ëŒى—گى„œ ê³µى£¼ë‹ک까ى§€ىک ë©کي•کيƒ„ 거리, â‘،)ê°€ ëگ©ë‹ˆë‹¤. (ë©کي•کيƒ„ 거리 : |x1−x2|+|y1−y2|) ëکگëٹ”, ê·¸ëŒى„ ى–»ى—ˆëٹ”ى§€ىک ى—¬ë¶€ë¥¼ 기ى–µي•´ 놓ىœ¼ë©´ى„œ, ê°€ى§€ê³ ىˆë‹¤ë©´ ë²½ى„ 무ى‹œي•کê³ ى§€ ë‚کëڈ„ë، BFS를 ëڈŒë¦¬ى…”ëڈ„ ëگ©ë‹ˆë‹¤.
- 6. C 달يŒ½ى´ 리ىٹ¤يٹ¸ ى œى¶œ : 265يڑŒ ى •ë‹µ : 27ëھ… (ى •ë‹µë¥ 10%) First Solve : ى†گXىڑ©ë‹ک (20분) ى¶œى œىگ : degurii
- 7. C 달يŒ½ى´ 리ىٹ¤يٹ¸ Kê°€ ى£¼ى–´ى§ˆ 때마다 ë°ک복문ى„ K번ى”© ëڈŒë¦¬ë©´ ى‹œê°„ ë³µى،ëڈ„ê°€ O(MK)ë،œ ى‹œê°„ ى´ˆê³¼ë¥¼ 받게 ëگ©ë‹ˆë‹¤. ىڑ°ى„ ى‹¸ى´يپ´ى—گ يڈ¬ي•¨ëگœ 노드ى™€ ê·¸ë ‡ى§€ ى•ٹى€ 노드를 ë”°ë،œ 관리ي•©ë‹ˆë‹¤. 1) K번 ى´ëڈ™ي•´ى„œ ëڈ„ى°©ي–ˆى„ ë•Œ ى‹¸ى´يپ´ى—گ يڈ¬ي•¨ëگœ 노드가 ى•„니ë¼ë©´, ى‰½ê²Œ 구ي• ىˆک ىˆىٹµë‹ˆë‹¤. 2) K번 ى´ëڈ™ي•´ى„œ ëڈ„ى°©ي•œ 노드가 ى‹¸ى´يپ´ى—گ يڈ¬ي•¨ëگœë‹¤ë©´, (K-ى‹¸ى´يپ´ى—گ يڈ¬ي•¨ëگکى§€ ى•ٹى€ 노드 ىˆک)%(ى‹¸ى´يپ´ى—گ يڈ¬ي•¨ëگœ 노드 ىˆک) 를 ى¸ëچ±ىٹ¤ë،œ ى‚¬ىڑ©ي•´ى„œ ى؟¼ë¦¬ë‹¹ O(1)ë،œ 구ي• ىˆک ىˆىٹµë‹ˆë‹¤.
- 8. D 문ىگى—´ ي™”يڈگ ى œى¶œ : 150يڑŒ ى •ë‹µ : 26ëھ… (ى •ë‹µë¥ 17%) First Solve : ë°°Xë°کë‹ک (60분) ى¶œى œىگ : Green55
- 9. D 문ىگى—´ ي™”يڈگ ىµœëŒ€ي•œ ى™¼ىھ½ى—گ ى•ى„œëٹ” ى•ŒيŒŒë²³ى„ ëپ¼ى›Œ ë„£ëٹ”게 ىµœى پى…니다. ex) AAZZZZZZZ 보다ëٹ” ABAAAAAAAى´ ى•ى„ 다. ë”°ë¼ى„œ, ىµœëŒ€ي•œ ë’¤ىھ½ى—گ Z를 ى±„ى›Œë„£ى–´ى„œ 문ىگى—´ىک ê°€ى¹ک를 높ى´ê³ , ê°€ى¹کê°€ ى¶©ë¶„يˆ ى»¤ى،Œىœ¼ë©´ ى•ىھ½ى—” A를 ى±„ى›Œë„£ىœ¼ë©´ ëگ©ë‹ˆë‹¤. ى¦‰, 답ى€ 기본ى پىœ¼ë،œ “AA..AA[?]ZZ..ZZâ€ىک يک•يƒœى…니다. ([?] = ى–´ë–¤ ى•ŒيŒŒë²³)
- 10. D 문ىگى—´ ي™”يڈگ i번ى§¸ ى•ŒيŒŒë²³ى´ 무ى—‡ى„ ë„£ى„ى§€ ê²°ى •ي•´ë´…ى‹œë‹¤. 1~(i-1)ى„ Aë،œ ى±„ى›Œë„£ى—ˆى„ ë•Œ 문ىگى—´ىک ê°€ى¹کëٹ” 1أ—(i-1) + [i번ى§¸ ى•ŒيŒŒë²³ىک ê°€ى¹ک] + 26أ—(N-i) ë”°ë¼ى„œ 1 <= X - 1أ—(i-1) - 26أ—(N-i) <= 26ى´ë¼ë©´, iى—گ X - 1أ—(i-1) - 26أ—(N-i)번ى§¸ ى•ŒيŒŒë²³ى„ ë„£ê³ , 1~(i-1)ى„ Aë،œ ى±„ى›Œë„£ى„ ىˆک ىˆىٹµë‹ˆë‹¤. ê·¸ë ‡ى§€ ى•ٹ다면, iى—گëٹ” Z를 ى±„ى›Œى•¼ي•©ë‹ˆë‹¤. 1 2 ... i-1 i i+1 ... N-1 N ... ? Z Z Z
- 11. D 문ىگى—´ ي™”يڈگ ىکˆى™¸ : ى „부 Aë،œ ى±„ى›Œëڈ„ ى•ˆ ëگ 만يپ¼ Xê°€ 너무 ى‘ê±°ë‚ک, ى „부 Zë،œ ى±„ى›Œëڈ„ ى•ˆ ëگ 만يپ¼ Xê°€ 너무 يپ¬ë©´ 불가ëٹ¥ي•©ë‹ˆë‹¤. (ى¶œë ¥ى´ˆê³¼ë¥¼ ë°›ىœ¼ى‹ 분들ى€, 대부분 ى‘ى€ ê²½ىڑ°ë¥¼ ى²ک리ي•کى§€ ى•ٹى•„ى„œ ى…니다.)
- 12. E 222-ي’€ë§پ ى œى¶œ : 32يڑŒ ى •ë‹µ : 27ëھ… (ى •ë‹µë¥ 84%) First Solve : ى´Xى‹ë‹ک (52분) ى¶œى œىگ : degurii
- 13. E 222-ي’€ë§پ 본문ى—گ ë‚کىک¨ 대ë،œ 구يک„만 ي•کë©´ ëگکëٹ” 문ى œى…니다. ى„¤ëھ…ي•ک기가 ى• 매ي•ک니 ى½”ë“œë،œ 대ى²´ي•©ë‹ˆë‹¤. int n, p[1100][1100]; int snd_max(int x, int y) { vector<int> t; for (int i = x; i < x + 2; i++) { for (int j = y; j < y + 2; j++) { t.push_back(p[i][j]); } } sort(t.begin(), t.end()); return t[2]; }
- 14. E 222-ي’€ë§پ int main() { cin >> n; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { cin >> p[i][j]; } } while (n > 1) { for (int i = 0; i < n / 2; i++) { for (int j = 0; j < n / 2; j++) { int x = i * 2, y = j * 2; p[i][j] = snd_max(x, y); } } n /= 2; } cout << p[0][0]; }
- 15. F ى´ى§„ىˆکى”¨ىک ي•ک루 ى¼ê³¼ ى œى¶œ : 18يڑŒ ى •ë‹µ : 5ëھ… (ى •ë‹µë¥ 28%) First Solve : ى´Xيک•ë‹ک (118분) ى¶œى œىگ : Green55
- 16. F ى´ى§„ىˆکى”¨ىک ي•ک루 ى¼ê³¼ “ ى§„ىˆکى”¨ëٹ” ê·¸ىک ى¼ىƒ ëڈ™ى•ˆىک ê²½ي—کىœ¼ë،œ يپ° ى´ى§„ىˆک를 ë¹ ë¥´ê²Œ ê³±ي•کëٹ” 것ى€ 매ىڑ° ى–´ë µë‹¤ëٹ” 것ى„ ى•Œê³ ىˆë‹¤. †يڈ‰ë²”ي•ک게 ê³±ى…ˆ ى•Œê³ 리ى¦کى„ 구يک„ي•œë‹¤ë©´, O(Nآ²)ى´ 걸립니다. ى´ê²ƒë³´ë‹¤ ë¹ ë¥¸ ê³±ى…ˆ ى•Œê³ 리ى¦کى€ 구يک„ى´ ى–´ë µىٹµë‹ˆë‹¤. (ى¹´ë¼ى¸ ë°”, FFT등ىœ¼ë،œ O(NlogN)) ë”°ë¼ى„œ ىˆک를 ى§پى ‘ ê³±ي•کى§€ ë§گê³ , ê³±ي–ˆى„ ë•Œ ê²°ê³¼ىک 길ى´ë§Œ ë¹ ë¥´ê²Œ 구ي•کëٹ” 방법ى„ ىƒê°پي•´ë´…ى‹œë‹¤.
- 17. F ى´ى§„ىˆکى”¨ىک ي•ک루 ى¼ê³¼ ?를 ى „부 1ë،œ ى±„ى› ى„ ë•Œ ë‘گ ê³±ىک ê°’ى´ ى œى¼ يپ¬ê³ , ?를 ى „부 0ë،œ ى±„ى› ى„ ë•Œ ë‘گ ê³±ىک ê°’ى´ ى œى¼ ى‘ىٹµë‹ˆë‹¤. ë”°ë¼ى„œ ê·¸ë ‡ê²Œ ى±„ىڑ´ ي›„, Aى™€ Bىک ê³±ىک 길ى´ë§Œ يŒگ별ي•´ë´…ى‹œë‹¤. ex) B = 0?1??ë©´, ىµœى†Œê°’ : 11111أ—0?1?? → 11111أ—00100 → 11111أ—100 ë…¼ىک를 ىœ„ي•´ B ى•ى—گ ى“¸ëچ° ى—†ëٹ” 0ى€ 떼버립니다. يژ¸ىکىƒپ ى´ëں° Bىک 길ى´ë¥¼ Mى´ë¼ê³ ي•´ë³´ê² ىٹµë‹ˆë‹¤. (ىœ„ىک ىکˆëٹ” M = 3)
- 18. F ى´ى§„ىˆکى”¨ىک ي•ک루 ى¼ê³¼ ê´€ى°° 1 : Aأ—Bëٹ” ى•„무리 ى»¤ëڈ„ ىµœëŒ€ (N+M)ىگ리ى´ë‹¤. Bê°€ ê°€ى¥ يپ° ê²½ىڑ°ëٹ” 111...11ى¼ ë•Œ ى…니다. ى´ ê²½ىڑ°,
- 19. F ى´ى§„ىˆکى”¨ىک ي•ک루 ى¼ê³¼ ê´€ى°° 2 : Aأ—Bëٹ” ى•„무리 ى‘ى•„ëڈ„ ىµœى†Œ (N+M-1)ىگ리ى´ë‹¤. Bê°€ ê°€ى¥ ى‘ى€ ê²½ىڑ°ëٹ” 100...00ى¼ ë•Œ ى…니다. ى´ ê²½ىڑ°, ëھ…ë°±ي•ک게 (N+M-1)ىگ리ى…니다. 111111 أ— 1000 111111000
- 20. F ى´ى§„ىˆکى”¨ىک ي•ک루 ى¼ê³¼ ê·¸ë ‡ë‹¤ë©´ 답ى€ N+M, N+M-1 ى¤‘ ي•کë‚کى…니다. ê·¸ëں°ëچ° ى œى¼ ى‘ى€ B=1000보다 ë”± 1 ëچ” يپ° B=1001ى¼ ë•Œ, 111111أ—1001 = (111111أ—1000) + 111111 ىک¬ë¦¼ى´ ى¼ى–´ë‚کى„œ N+M-1ىگ리를 ë„کى–´ë²„립니다. (111111000ى€, 1000만 ëچ”ي•´ëڈ„ ىک¬ë¦¼ى´ ى¼ى–´ë‚©ë‹ˆë‹¤.) ë”°ë¼ى„œ, Bê°€ 100...00 ê¼´ى´ë©´ 답ى€ N+M-1 ى´ê³ , 맨 ى• 비يٹ¸ ى™¸ى—گ 1ى´ ي•کë‚کë¼ëڈ„ ىˆىœ¼ë©´ 답ى€ N+M ى…니다. ىکˆى™¸ : B = 1ى„ ى£¼ىکي•کى„¸ىڑ”! Bëٹ” 맨 ى• 비يٹ¸ ى™¸ى—گ 1ى¸ 비يٹ¸ê°€ ى—†ىٹµë‹ˆë‹¤. 111111 أ— 1000 111111000 + 111111 1000110111
- 21. F ى´ى§„ىˆکى”¨ىک ي•ک루 ى¼ê³¼ ي•کى§€ë§Œâ€¦ ê²€ىˆک ë•Œëٹ” ى œê°€ يŒŒى´ىچ¬ىœ¼ë،œ ى‹œê°„ى´ˆê³¼ê°€ 났ëٹ”ëچ°, 본대يڑŒ ى¤‘ ي•™ىڑ°ë¶„ê»کى„œ ë‘گ ى´ى§„ىˆک를 ى§پى ‘ ê³±ي•کëٹ” 방법ىœ¼ë،œ ي’€ى–´ë²„ë ¸ىٹµë‹ˆë‹¤ (يŒŒى´ىچ¬ى€ يپ° ىˆکىک ى—°ى‚°ى„ ى§€ى›گي•©ë‹ˆë‹¤) ى œê°€ 부ى،±ي•œ 따름ى…니다. ى£„ى†،ي•©ë‹ˆë‹¤ ًںک¢
- 22. G ë©´ى ‘ë³´ëٹ” ىٹ¹ë²”ى´ë„¤ ى œى¶œ : 7يڑŒ ى •ë‹µ : 1ëھ… (ى •ë‹µë¥ 14%) First Solve : ى´Xى„±ë‹ک (173분) ى¶œى œىگ : degurii
- 23. G ë©´ى ‘ë³´ëٹ” ىٹ¹ë²”ى´ë„¤ 문ى œë¥¼ ي•´ê²°ي•ک기 ىœ„ي•´ ê·¸ëکي”„ىک ê°پ 노드ى—گى„œ ê°€ى¥ 가까ىڑ´ ë©´ى ‘ى¥ê¹Œى§€ىک ىµœë‹¨ 거리를 구ي•´ى•¼ ي•©ë‹ˆë‹¤. ë”°ë¼ى„œ ىµœë‹¨ 거리 ى•Œê³ 리ى¦ک, يٹ¹يˆ 다ىµىٹ¤يٹ¸ë¼ë¥¼ ىچ¨ى•¼ ي•œë‹¤ëٹ” 것ى„ ى•Œ ىˆک ىˆىٹµë‹ˆë‹¤. ي•کى§€ë§Œ ëھ¨ë“ 노드ى—گى„œ 다ىµىٹ¤يٹ¸ë¼ë¥¼ ëڈŒë ¤ 답ى„ 구ي• ê²½ىڑ°, O(VElogE)ë،œ ى‹œê°„ى´ˆê³¼ë¥¼ 받게 ëگ©ë‹ˆë‹¤. ى´ë¥¼ ي•´ê²°ي•ک기 ىœ„ي•´ ى•Œى•„ى•¼ ي• ë‘گ ê°€ى§€ë¥¼ 다ىŒ يژکى´ى§€ى—گى„œ ى„¤ëھ…ي•©ë‹ˆë‹¤.
- 24. G ë©´ى ‘ë³´ëٹ” ىٹ¹ë²”ى´ë„¤ 1) ى— ê·¸ëکي”„ى—گى„œ ëڈŒë¦° 다ىµىٹ¤يٹ¸ë¼ ي•œ 번ىœ¼ë،œ ى›گ본 ê·¸ëکي”„ىک ëھ¨ë“ 노드ى—گى„œ يٹ¹ى • 노드 x까ى§€ىک ىµœ 단 ê²½ë،œë¥¼ 구ي• ىˆک ىˆىٹµë‹ˆë‹¤. ى„ىکىک ê·¸ëکي”„ى™€ ê·¸ ê·¸ëکي”„ىک ê°„ى„ ë°©ي–¥ى„ ë’¤ى§‘ى€ ى— ë°©ي–¥ ê·¸ëکي”„ê°€ ىˆë‹¤ê³ ي•©ى‹œë‹¤. ى´ë•Œ ى—ë°©ي–¥ ê·¸ëکي”„ى—گى„œ 노드 x를 ى‹œى‘ى گىœ¼ë،œ 다ىµىٹ¤ يٹ¸ë¼ë¥¼ ëڈŒë ¤ 거리배ى—´ dst[]를 ى–»ى„ ىˆک ىˆëٹ”ëچ°, ى›گ본 ê·¸ ëکي”„ى™€ ى— ê·¸ëکي”„ى—گى„œ ي•´ى„ى´ 달ë¼ى§‘니다. ى— ê·¸ëکي”„ى—گى„œ dst[i]ëٹ” x->i까ى§€ىک ىµœë‹¨ 거리ى´ê³ , 놀 ëچ게ëڈ„ ى›گ본 ê·¸ëکي”„ى—گى„œىک dst[i]ëٹ” i->x까ى§€ىک ىµœë‹¨ 거리를 뜻ي•©ë‹ˆë‹¤. [ى›گ본 ê·¸ëکي”„] [ى—ë°©ي–¥ ê·¸ëکي”„]
- 25. G ë©´ى ‘ë³´ëٹ” ىٹ¹ë²”ى´ë„¤ 2) 다ىµىٹ¤يٹ¸ë¼ ى•Œê³ 리ى¦کى€ ى‹œى‘ى گى´ ى—¬ëں¬ ê°œى—¬ëڈ„ ëگ©ë‹ˆë‹¤. ë³´ي†µ 다ىµىٹ¤يٹ¸ë¼ ى•Œê³ 리ى¦کى—گى„œ ى‹œى‘ى گى€ ي•کë‚ک만 ىˆى–´ى•¼ ي•œë‹¤ê³ ىƒê°پي• ىˆک ىˆىٹµë‹ˆë‹¤. ي•کى§€ë§Œ 다ىµىٹ¤يٹ¸ë¼ىک ى›گ리가 â€کيک„ى¬ê¹Œى§€ ىµœë‹¨ 거리ى„ى´ ë³´ى¥ëگœ ى •ى گ’들ىک ى½”ىٹ¤يٹ¸ë¥¼ 기ë°کىœ¼ë،œ â€کى•„ى§پ ë³´ى¥ëگکى§€ ى•ٹى€ ى •ى گ’ ى¤‘ ى½”ىٹ¤يٹ¸ê°€ ê°€ى¥ ى‘ى€ ى •ى گى„ ي™•ى¥ي•´ë‚کê°€ëٹ” ë°©ى‹ى¸ 것ى„ ىƒê°پي•´ë³´ë©´ ى‹œى‘ى گى´ ى—¬ëں¬ ê°œى—¬ëڈ„ ىƒپ ê´€ى—†ë‹¤ëٹ” 것ى„ ى•Œ ىˆک ىˆىٹµë‹ˆë‹¤. ىµœë‹¨ 거리ى„ى„ ë³´ى¥ي•ک기만 ي•œë‹¤ë©´ىڑ”! ى—¬ëں¬ ê°œىک ى‹œى‘ى گ v1, v2, …, vn ى´ ىˆى„ ë•Œ ê°پ ى گىک ىµœë‹¨ 거리ëٹ” 당ى—°يˆ 0ى¼ 것ى´ë‹ˆ, 거리를 0ىœ¼ë،œ ى„¤ى •ي•ک ê³ ى‹œى‘ى گ ëھ¨ë‘گ를 يپگى—گ ë„£ى–´ 다ىµىٹ¤يٹ¸ë¼ë¥¼ ëڈŒë¦¬ë©´ ëگ©ë‹ˆë‹¤. ê·¸ ê²°ê³¼ë،œ ى–»ëٹ” ىµœë‹¨ 거리ëٹ” ى–´ë–¤ ى‹œى‘ى گى—گى„œ ى¶œë°œي–ˆëٹ”ى§€ëٹ” ى•Œ ىˆک ى—†ى§€ë§Œ, ى–´ى¨Œë“ ى‹œى‘ى گى—گى„œ ى¶œë°œي•´ ى„ىک ىک 노드까ى§€ ê°€ëٹ” ê°€ى¥ ى§§ى€ 거리ë¼ëٹ” 뜻ى…니다.
- 26. G ë©´ى ‘ë³´ëٹ” ىٹ¹ë²”ى´ë„¤ 문ى œë¥¼ ي•´ê²°ي•ک기 ىœ„ي•´ ى•ى—گى„œ ى„¤ëھ…ي•œ ë‘گ ê°€ى§€ë¥¼ ي•œ 번ى—گ ى‚¬ىڑ©ي•کë©´ ëگ©ë‹ˆë‹¤. ىڑ°ى„ ëھ¨ë“ ê°„ى„ ىک ë°©ي–¥ى„ ë’¤ى§‘ىٹµë‹ˆë‹¤. ى´ ê·¸ëکي”„ى—گى„œ ى„ىکىک ë©´ى ‘ى¥ x를 ى‹œى‘ى گىœ¼ë،œ 다ىµىٹ¤يٹ¸ë¼ë¥¼ ëڈŒë¦¬ë©´ ى›گ본 ê·¸ëکي”„ىک (ëھ¨ë“ 노드들→x) 까ى§€ىک ىµœë‹¨ 거리를 구ي• ىˆک ىˆىٹµë‹ˆë‹¤. (1 ≤ ë©´ى ‘ى¥ىک ê°œىˆک ≤ N) ى´ë¯€ë،œ ê°پ ë©´ى ‘ى¥ë§ˆë‹¤ 다ىµىٹ¤يٹ¸ë¼ë¥¼ ëڈŒë¦¬ë©´ ى‹œê°„ ى´ˆê³¼ى…니다. ê·¸ëں¬ى§€ ى•ٹê³ ëھ¨ë“ ë©´ى ‘ى¥ى„ ي•œ 번ى—گ يپگى—گ ë„£ى–´ 다ىµىٹ¤يٹ¸ë¼ë¥¼ ëڈŒë¦¬ë©´ ى‹œê°„ë‚´ى—گ 문ى œë¥¼ ي•´ê²°ي• ىˆک ىˆىٹµë‹ˆë‹¤.
- 27. I 대기ى—… ىٹ¹ë²”ى´ë„¤ ى œى¶œ : 0يڑŒ ى •ë‹µ : 0ëھ… First Solve : - ى¶œى œىگ : Green55
- 28. I 대기ى—… ىٹ¹ë²”ى´ë„¤ ى–´ë–¤ 노드 Xى™€, Xىک ىگى†گ들ى„ ى „부 ى„ يƒي•کë©´ يٹ¸ë¦¬ى…니다. ى´ê²ƒى„ Xىک ى„œë¸Œيٹ¸ë¦¬ë¼ê³ ي•©ë‹ˆë‹¤. ى´ëں° ى„±ى§ˆى„ ى´ىڑ©ي•´ى„œ, يٹ¸ë¦¬ى—گëڈ„ DP를 ى پىڑ© ى‹œي‚¬ ىˆک ىˆىٹµë‹ˆë‹¤. يٹ¸ë¦¬ DPëٹ” يƒ‘-다ىڑ´(ى¬ê·€ ë°©ى‹)ىœ¼ë،œ ي•کëٹ”게 يژ¸ي•©ë‹ˆë‹¤. ë°”ي…€-ى—…(ë°ک복문)ى„ ى‚¬ىڑ©ي•کë ¤ë©´, يٹ¸ë¦¬ىک 높ى´ë¥¼ يŒŒى•…ي•´ ى•„ëک부ي„° ى±„ى›Œë‚کê°€ى•¼ ي•ک기 때문ى—گ ى–´ى°¨ي”¼ DFS를 ي•œë²ˆ ëڈŒë ¤ى•¼ي•©ë‹ˆë‹¤.
- 29. I 대기ى—… ىٹ¹ë²”ى´ë„¤ Xىک ى„œë¸Œيٹ¸ë¦¬ ى•ˆى—گى„œ ىµœى پىک 답ى„ 구ي• ë•Œ, X ë§گê³ ëٹ” ى„œë¸Œيٹ¸ë¦¬ ى™¸ë¶€ى™€ ë©کي† ë§پى„ ë§؛ى„ ê°€ëٹ¥ى„±ى´ ى—†ىٹµë‹ˆë‹¤. ى¦‰, Xê°€ Xىک ى‚¬ىˆکى™€ ë©کي† ë§پى„ ي•کëٹ”ى§€ىک ى—¬ë¶€ ى™¸ى—گëٹ”, ى„œë¸Œيٹ¸ë¦¬ ى™¸ë¶€ىک ë©کي† ë§پ 관계를 기ى–µ ي• ي•„ىڑ”ê°€ ى—†ىٹµë‹ˆë‹¤. ë”°ë¼ى„œ 다ىŒê³¼ ê°™ى€ ى گي™”ى‹ى„ ى„¸ى›Œë´…ى‹œë‹¤. dp[X][hasMento] = Xê°€ Xىک ى‚¬ىˆکى™€ ë©کي† ë§پى„ ë§؛ى„ ë•Œ(hasMento=1), يک¹ى€ ë§؛ى§€ ى•ٹى„ ë•Œ(hasMento=0), X ىک ى„œë¸Œيٹ¸ë¦¬ى—گى„œىک ى‹œë„ˆى§€ىک ي•©ىک ىµœëŒ€ê°’
- 30. I 대기ى—… ىٹ¹ë²”ى´ë„¤ ى¼€ى´ىٹ¤ 1 : Xê°€ Xىک ى‚¬ىˆکى™€ ë©کي† ë§پى„ ë§؛ى„ ë•Œ Xëٹ” ى´ë¯¸ ë©کي† ê°€ ىˆىœ¼ë‹ˆ, Xىک 부ى‚¬ىˆک들ى€ X를 ë©کي† ë،œ ê°€ى§ˆ ىˆک ى—†ىٹµë‹ˆë‹¤. 그냥 Xىک 부ى‚¬ىˆک들ىک ى„œë¸Œيٹ¸ë¦¬ى—گى„œ, ىµœى پىک 답ى„ 구ي•´ ى „부 ëچ”ي•´ى£¼ë©´ ëگ©ë‹ˆë‹¤. Xىک 부ى‚¬ىˆک를 C1, C2, C3, … ë¼ê³ ي•کë©´ dp[X][1] = dp[C1][0] + dp[C2][0] + dp[C3][0]…
- 31. I 대기ى—… ىٹ¹ë²”ى´ë„¤ ى¼€ى´ىٹ¤ 2 : Xê°€ Xىک ى‚¬ىˆکى™€ ë©کي† ë§پى„ ë§؛ى§€ ى•ٹى„ ë•Œ ى¼€ى´ىٹ¤ 1ى—گى„œ ى¶”ê°€ë،œ, Xى™€ Xىک 부ى‚¬ىˆک ي•œëھ…ى´ ë©کي† ë§پ ي•کëٹ” ê²½ىڑ°ëڈ„ ê³ ë ¤ي•´ى•¼ ي•©ë‹ˆë‹¤. dp[X][1] = max{ dp[C1][0] + dp[C2][0] + … // Xê°€ ى•„무ى™€ëڈ„ ë©کي† ë§پ ي•کى§€ ى•ٹىŒ ى‹¤ë ¥[X]*ى‹¤ë ¥[C1] + dp[C1][1] + dp[C2][0] + … // Xى™€ C1ى´ ë©کي† ë§پى„ ë§؛ىŒ ى‹¤ë ¥[X]*ى‹¤ë ¥[C2] + dp[C1][0] + dp[C2][1] + … // Xى™€ C1ى´ ë©کي† ë§پى„ ë§؛ىŒ ...
- 32. I 대기ى—… ىٹ¹ë²”ى´ë„¤ ى‹¤ë ¥[X]*ى‹¤ë ¥[C1] + dp[C1][1] + dp[C2][0] + … â‘ ى‹¤ë ¥[X]*ى‹¤ë ¥[C2] + dp[C1][0] + dp[C2][1] + … â‘، … ى„ ى „부 ى¼ى¼ى´ 구ي•کë©´, ى‹œê°„ى´ 너무 ىک¤ëک걸립니다. (ىگى‹ىک ىˆکê°€ Cë©´, O(Cآ²)) ë”°ë¼ى„œ (dp[C1][0] + dp[C2][0] + dp[C3][0]...)ى„ 미리 O(C)ë،œ 구ي•´ë†“ê³ , â‘ = (dp[C1][0] + dp[C2][0] + dp[C3][0]...) - dp[C1][0] + dp[C1][1] + ى‹¤ë ¥[X]*ى‹¤ë ¥[C1] â‘، = (dp[C1][0] + dp[C2][0] + dp[C3][0]...) - dp[C2][0] + dp[C2][1] + ى‹¤ë ¥[X]*ى‹¤ë ¥[C2] ë©´ ي•کë‚ک당 O(1)ى—گ 구ي• ىˆک ىˆىٹµë‹ˆë‹¤.
- 33. J ى‚¬ىگى™€ ي† ëپ¼ ى œى¶œ : 3يڑŒ ى •ë‹µ : 0ëھ… First Solve : - ى¶œى œىگ : Green55
- 34. J ى‚¬ىگى™€ ي† ëپ¼ ى™ 만ي•کë©´ 게ى„ى´ ëپ납니다. 게ى„ى´ ëپë‚کى§€ ى•ٹىœ¼ë ¤ë©´, ي† ëپ¼ى™€ ى‚¬ىگê°€ ى•„무리 ë…¸ë ¥ي•´ëڈ„ ë§Œë‚ ىˆک ى—†ëٹ” يٹ¹ىˆکي•œ ى¼€ى´ىٹ¤ىک ê·¸ëکي”„ى—¬ى•¼ي•©ë‹ˆë‹¤. ى´ëں° ê·¸ëکي”„ëٹ” ى–´ë–»ê²Œ ىƒê²¼ى„까ىڑ”?
- 35. J ى‚¬ىگى™€ ي† ëپ¼ ي™€ىˆک번ى§¸ ي„´ى—گëٹ” ي† ëپ¼ëٹ” ي•ىƒپ ى™¼ىھ½ ىˆکي’€ى—گ, ى‚¬ىگëٹ” ي•ىƒپ ىک¤ë¥¸ىھ½ ىˆکي’€ى—گ ىˆىٹµë‹ˆë‹¤. ى§ىˆک번ى§¸ ي„´ى—گëٹ” ى‚¬ىگëٹ” ي•ىƒپ ى™¼ىھ½ ىˆکي’€ى—گ, ي† ëپ¼ëٹ” ي•ىƒپ ىک¤ë¥¸ىھ½ ىˆکي’€ى—گ ىˆىٹµë‹ˆë‹¤. ى´ëں¬ë©´ ë‘کى´ ي•ىƒپ ى—‡ê°ˆë ¤ى„œ ى ˆëŒ€ ë§Œë‚ ىˆک ى—†ىٹµë‹ˆë‹¤.
- 36. J ى‚¬ىگى™€ ي† ëپ¼ ىƒ‰ى„ ى¹ ي•´ë³´ê² ىٹµë‹ˆë‹¤. 빨간 ىˆکي’€ê³¼ ى¸ى ‘ي•œ 빨간 ىˆکي’€ى€ ي•کë‚کëڈ„ ى—†ىٹµë‹ˆë‹¤. يŒŒë€ ىˆکي’€ëڈ„ 마ى°¬ê°€ى§€ى…니다. ى´ëں° ê·¸ëکي”„를 ى´ë¶„ ê·¸ëکي”„(Bipartite Graph) ë¼ê³ ي•©ë‹ˆë‹¤.
- 37. J ى‚¬ىگى™€ ي† ëپ¼ ى•„무 ى •ى گى´ë‚ک ى،ê³ ë¹¨ê°„ىƒ‰ىœ¼ë،œ ى¹ ي•©ى‹œë‹¤. DFSë‚ک BFSë،œ ê·¸ëکي”„를 ىˆœيڑŒي•کë©°, يک„ى¬ ى •ى گê³¼ ى¸ى ‘ي•œ ى •ى گ ى¤‘ ى²کىŒ 방문ي•کëٹ” ى •ى گ, ى¦‰ ىƒ‰ى¹ ëگکى§€ ى•ٹى€ ى •ى گى„ ى°¾ى•کىœ¼ë©´ ê·¸ ىƒ‰ى„ يک„ى¬ ى •ى گê³¼ ë°ک대 ىƒ‰ىœ¼ë،œ ى¹ ي•©ë‹ˆë‹¤. ى´ë ‡ê²Œ ى¹ ي•œ ي›„, ê°™ى€ ىƒ‰ى¸ ىˆکي’€ى„ ى—°ê²°ي•کëٹ” 길ى´ ي•کë‚کë¼ëڈ„ ىˆë‹¤ë©´, ى´ë¶„ ê·¸ëکي”„ê°€ ى•„니므ë،œ 답ى€ 0ى…니다. (ىک 구يک„ي•کë©´ BFS/DFS ي•œ 번ىœ¼ë،œëڈ„ ê°€ëٹ¥ي•©ë‹ˆë‹¤.)
- 38. J ى‚¬ىگى™€ ي† ëپ¼ ى´ë¶„ ê·¸ëکي”„ë¼ë©´, 빨간ىƒ‰ ى •ى گىک ê°œىˆک = R يŒŒë€ىƒ‰ ى •ى گىک ê°œىˆک = B ى¼ ë•Œ 답ى€ R * B * 2ى…니다. (ي† ëپ¼ê°€ ى™¼ىھ½, ى‚¬ىگê°€ ىک¤ë¥¸ىھ½ى—گ ى‹œى‘ي•کëٹ” ê²½ىڑ° R*B + ي† ëپ¼ê°€ ىک¤ë¥¸ىھ½, ى‚¬ىگê°€ ى™¼ىھ½ى—گى„œ ى‹œى‘ي•کëٹ” ê²½ىڑ° R*B)
- 39. K ي™چىµëŒ€ي•™êµگ ى§€ي•کى؛ يچ¼ىٹ¤ ى œى¶œ : 0يڑŒ ى •ë‹µ : 0ëھ… First Solve : - ى¶œى œىگ : rltjqdl1138
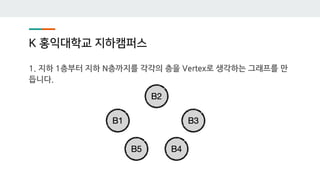
- 40. K ي™چىµëŒ€ي•™êµگ ى§€ي•کى؛ يچ¼ىٹ¤ 1. ى§€ي•ک 1ى¸µë¶€ي„° ى§€ي•ک Nى¸µê¹Œى§€ë¥¼ ê°پê°پىک ى¸µى„ Vertexë،œ ىƒê°پي•کëٹ” ê·¸ëکي”„를 만 ë“니다.
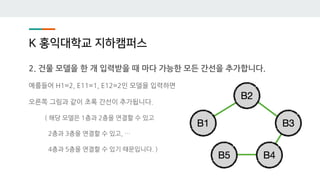
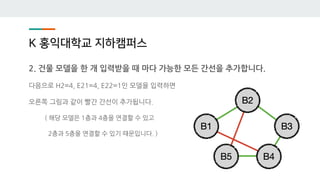
- 41. K ي™چىµëŒ€ي•™êµگ ى§€ي•کى؛ يچ¼ىٹ¤ 2. 건물 ëھ¨ëچ¸ى„ ي•œ ê°œ ى…ë ¥ë°›ى„ ë•Œ 마다 ê°€ëٹ¥ي•œ ëھ¨ë“ ê°„ى„ ى„ ى¶”ê°€ي•©ë‹ˆë‹¤. ىکˆë¥¼ë“¤ى–´ H1=2, E11=1, E12=2ى¸ ëھ¨ëچ¸ى„ ى…ë ¥ي•کë©´ ىک¤ë¥¸ىھ½ 그림과 ê°™ى´ ى´ˆë، ê°„ى„ ى´ ى¶”ê°€ëگ©ë‹ˆë‹¤. ( ي•´ë‹¹ ëھ¨ëچ¸ى€ 1ى¸µê³¼ 2ى¸µى„ ى—°ê²°ي• ىˆک ىˆê³ 2ى¸µê³¼ 3ى¸µى„ ى—°ê²°ي• ىˆک ىˆê³ , … 4ى¸µê³¼ 5ى¸µى„ ى—°ê²°ي• ىˆک ىˆê¸° 때문ى…니다. )
- 42. K ي™چىµëŒ€ي•™êµگ ى§€ي•کى؛ يچ¼ىٹ¤ 2. 건물 ëھ¨ëچ¸ى„ ي•œ ê°œ ى…ë ¥ë°›ى„ ë•Œ 마다 ê°€ëٹ¥ي•œ ëھ¨ë“ ê°„ى„ ى„ ى¶”ê°€ي•©ë‹ˆë‹¤. 다ىŒىœ¼ë،œ H2=4, E21=4, E22=1ى¸ ëھ¨ëچ¸ى„ ى…ë ¥ي•کë©´ ىک¤ë¥¸ىھ½ 그림과 ê°™ى´ 빨간 ê°„ى„ ى´ ى¶”ê°€ëگ©ë‹ˆë‹¤. ( ي•´ë‹¹ ëھ¨ëچ¸ى€ 1ى¸µê³¼ 4ى¸µى„ ى—°ê²°ي• ىˆک ىˆê³ 2ى¸µê³¼ 5ى¸µى„ ى—°ê²°ي• ىˆک ىˆê¸° 때문ى…니다. )
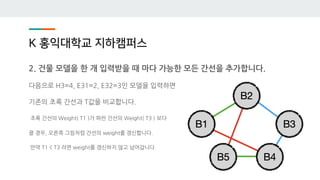
- 43. K ي™چىµëŒ€ي•™êµگ ى§€ي•کى؛ يچ¼ىٹ¤ 2. 건물 ëھ¨ëچ¸ى„ ي•œ ê°œ ى…ë ¥ë°›ى„ ë•Œ 마다 ê°€ëٹ¥ي•œ ëھ¨ë“ ê°„ى„ ى„ ى¶”ê°€ي•©ë‹ˆë‹¤. 다ىŒىœ¼ë،œ H3=4, E31=2, E32=3ى¸ ëھ¨ëچ¸ى„ ى…ë ¥ي•کë©´ 기ى،´ىک ى´ˆë، ê°„ى„ ê³¼ Tê°’ى„ 비êµگي•©ë‹ˆë‹¤. ى´ˆë، ê°„ى„ ىک Weight( T1 )ê°€ يŒŒë€ ê°„ى„ ىک Weight( T3 ) 보다 يپ´ ê²½ىڑ°, ىک¤ë¥¸ىھ½ 그림ى²کëں¼ ê°„ى„ ىک weight를 ê°±ى‹ ي•©ë‹ˆë‹¤. 만ى•½ T1 < T3 ë¼ë©´ weight를 ê°±ى‹ ي•کى§€ ى•ٹê³ ë„کى–´ê°‘니다.
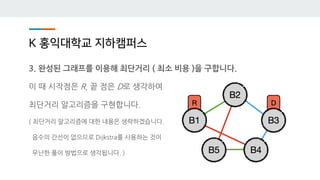
- 44. K ي™چىµëŒ€ي•™êµگ ى§€ي•کى؛ يچ¼ىٹ¤ 3. ى™„ى„±ëگœ ê·¸ëکي”„를 ى´ىڑ©ي•´ ىµœë‹¨ê±°ë¦¬ ( ىµœى†Œ 비ىڑ© )ى„ 구ي•©ë‹ˆë‹¤. ى´ ë•Œ ى‹œى‘ى گى€ R, ëپ ى گى€ Dë،œ ىƒê°پي•کى—¬ ىµœë‹¨ê±°ë¦¬ ى•Œê³ 리ى¦کى„ 구يک„ي•©ë‹ˆë‹¤. ( ىµœë‹¨ê±°ë¦¬ ى•Œê³ 리ى¦کى—گ 대ي•œ ë‚´ىڑ©ى€ ىƒëµي•کê² ىٹµë‹ˆë‹¤. ىŒىˆکىک ê°„ى„ ى´ ى—†ىœ¼ë¯€ë،œ Dijkstra를 ى‚¬ىڑ©ي•کëٹ” 것ى´ 무난ي•œ ي’€ى´ 방법ىœ¼ë،œ ىƒê°پëگ©ë‹ˆë‹¤. )

![A ë‚کىک ي•™ى گى€?
int score[51], my_score;
for(int i=1; i<=50; ++i)
scanf(“%dâ€, &score[i]);
scanf(“%dâ€, &my_score);
for(int i=1; i<=50; ++i){
if(score[i] == my_score){
//i등ى—گ ي•´ë‹¹ي•کëٹ”
//ي•™ى گى„ ى¶œë ¥
}
}
ى´ëں° ى‹¤ىˆک들ى´ ىˆى—ˆىٹµë‹ˆë‹¤ :
- ى¸ëچ±ىٹ¤ë¥¼ 0~49ë،œ ى،ى•کëٹ”ëچ°, 등ىˆکëٹ” 1~50
ىœ¼ë،œ ي™•ى¸ي•œë‹¤.
- score[]ى•ˆى—گ ë‚´ 등ىˆکê°€ ى—†ë‹¤ê³ ىƒê°پي•کê³ ,
ë°°ى—´ ë‚´ى—گى„œ ê°™ى€ ى گىˆکىک 등ىˆک를 ى°¾ى§€ ى•ٹëٹ”
다.](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-3-320.jpg)





![D 문ىگى—´ ي™”يڈگ
ىµœëŒ€ي•œ ى™¼ىھ½ى—گ ى•ى„œëٹ” ى•ŒيŒŒë²³ى„ ëپ¼ى›Œ ë„£ëٹ”게 ىµœى پى…니다.
ex) AAZZZZZZZ 보다ëٹ” ABAAAAAAAى´ ى•ى„ 다.
ë”°ë¼ى„œ, ىµœëŒ€ي•œ ë’¤ىھ½ى—گ Z를 ى±„ى›Œë„£ى–´ى„œ 문ىگى—´ىک ê°€ى¹ک를 높ى´ê³ ,
ê°€ى¹کê°€ ى¶©ë¶„يˆ ى»¤ى،Œىœ¼ë©´ ى•ىھ½ى—” A를 ى±„ى›Œë„£ىœ¼ë©´ ëگ©ë‹ˆë‹¤.
ى¦‰, 답ى€ 기본ى پىœ¼ë،œ “AA..AA[?]ZZ..ZZâ€ىک يک•يƒœى…니다. ([?] = ى–´ë–¤ ى•ŒيŒŒë²³)](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-9-320.jpg)
![D 문ىگى—´ ي™”يڈگ
i번ى§¸ ى•ŒيŒŒë²³ى´ 무ى—‡ى„ ë„£ى„ى§€ ê²°ى •ي•´ë´…ى‹œë‹¤.
1~(i-1)ى„ Aë،œ ى±„ى›Œë„£ى—ˆى„ ë•Œ 문ىگى—´ىک ê°€ى¹کëٹ” 1أ—(i-1) + [i번ى§¸ ى•ŒيŒŒë²³ىک ê°€ى¹ک] + 26أ—(N-i)
ë”°ë¼ى„œ 1 <= X - 1أ—(i-1) - 26أ—(N-i) <= 26ى´ë¼ë©´,
iى—گ X - 1أ—(i-1) - 26أ—(N-i)번ى§¸ ى•ŒيŒŒë²³ى„ ë„£ê³ , 1~(i-1)ى„ Aë،œ ى±„ى›Œë„£ى„ ىˆک ىˆىٹµë‹ˆë‹¤.
ê·¸ë ‡ى§€ ى•ٹ다면, iى—گëٹ” Z를 ى±„ى›Œى•¼ي•©ë‹ˆë‹¤.
1 2 ... i-1 i i+1 ... N-1 N
... ? Z Z Z](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-10-320.jpg)


![E 222-ي’€ë§پ
본문ى—گ ë‚کىک¨ 대ë،œ 구يک„만 ي•کë©´ ëگکëٹ” 문ى œى…니다.
ى„¤ëھ…ي•ک기가 ى• 매ي•ک니 ى½”ë“œë،œ 대ى²´ي•©ë‹ˆë‹¤.
int n, p[1100][1100];
int snd_max(int x, int y) {
vector<int> t;
for (int i = x; i < x + 2; i++) {
for (int j = y; j < y + 2; j++) {
t.push_back(p[i][j]);
}
}
sort(t.begin(), t.end());
return t[2];
}](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-13-320.jpg)
![E 222-ي’€ë§پ
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> p[i][j];
}
}
while (n > 1) {
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n / 2; j++) {
int x = i * 2, y = j * 2;
p[i][j] = snd_max(x, y);
}
}
n /= 2;
}
cout << p[0][0];
}](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-14-320.jpg)






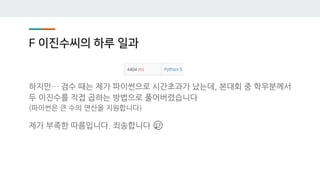


![G ë©´ى ‘ë³´ëٹ” ىٹ¹ë²”ى´ë„¤
1) ى— ê·¸ëکي”„ى—گى„œ ëڈŒë¦° 다ىµىٹ¤يٹ¸ë¼ ي•œ 번ىœ¼ë،œ ى›گ본
ê·¸ëکي”„ىک ëھ¨ë“ 노드ى—گى„œ يٹ¹ى • 노드 x까ى§€ىک ىµœ
단 ê²½ë،œë¥¼ 구ي• ىˆک ىˆىٹµë‹ˆë‹¤.
ى„ىکىک ê·¸ëکي”„ى™€ ê·¸ ê·¸ëکي”„ىک ê°„ى„ ë°©ي–¥ى„ ë’¤ى§‘ى€ ى—
ë°©ي–¥ ê·¸ëکي”„ê°€ ىˆë‹¤ê³ ي•©ى‹œë‹¤.
ى´ë•Œ ى—ë°©ي–¥ ê·¸ëکي”„ى—گى„œ 노드 x를 ى‹œى‘ى گىœ¼ë،œ 다ىµىٹ¤
يٹ¸ë¼ë¥¼ ëڈŒë ¤ 거리배ى—´ dst[]를 ى–»ى„ ىˆک ىˆëٹ”ëچ°, ى›گ본 ê·¸
ëکي”„ى™€ ى— ê·¸ëکي”„ى—گى„œ ي•´ى„ى´ 달ë¼ى§‘니다.
ى— ê·¸ëکي”„ى—گى„œ dst[i]ëٹ” x->i까ى§€ىک ىµœë‹¨ 거리ى´ê³ , 놀
ëچ게ëڈ„ ى›گ본 ê·¸ëکي”„ى—گى„œىک dst[i]ëٹ” i->x까ى§€ىک ىµœë‹¨
거리를 뜻ي•©ë‹ˆë‹¤.
[ى›گ본 ê·¸ëکي”„] [ى—ë°©ي–¥ ê·¸ëکي”„]](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-24-320.jpg)
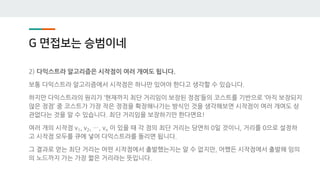
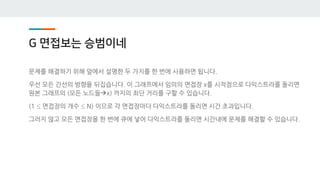


![I 대기ى—… ىٹ¹ë²”ى´ë„¤
Xىک ى„œë¸Œيٹ¸ë¦¬ ى•ˆى—گى„œ ىµœى پىک 답ى„ 구ي• ë•Œ,
X ë§گê³ ëٹ” ى„œë¸Œيٹ¸ë¦¬ ى™¸ë¶€ى™€ ë©کي† ë§پى„ ë§؛ى„ ê°€ëٹ¥ى„±ى´ ى—†ىٹµë‹ˆë‹¤.
ى¦‰, Xê°€ Xىک ى‚¬ىˆکى™€ ë©کي† ë§پى„ ي•کëٹ”ى§€ىک ى—¬ë¶€ ى™¸ى—گëٹ”,
ى„œë¸Œيٹ¸ë¦¬ ى™¸ë¶€ىک ë©کي† ë§پ 관계를 기ى–µ ي• ي•„ىڑ”ê°€ ى—†ىٹµë‹ˆë‹¤.
ë”°ë¼ى„œ 다ىŒê³¼ ê°™ى€ ى گي™”ى‹ى„ ى„¸ى›Œë´…ى‹œë‹¤.
dp[X][hasMento] =
Xê°€ Xىک ى‚¬ىˆکى™€ ë©کي† ë§پى„ ë§؛ى„ ë•Œ(hasMento=1), يک¹ى€ ë§؛ى§€ ى•ٹى„ ë•Œ(hasMento=0), X
ىک ى„œë¸Œيٹ¸ë¦¬ى—گى„œىک ى‹œë„ˆى§€ىک ي•©ىک ىµœëŒ€ê°’](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-29-320.jpg)
![I 대기ى—… ىٹ¹ë²”ى´ë„¤
ى¼€ى´ىٹ¤ 1 : Xê°€ Xىک ى‚¬ىˆکى™€ ë©کي† ë§پى„ ë§؛ى„ ë•Œ
Xëٹ” ى´ë¯¸ ë©کي† ê°€ ىˆىœ¼ë‹ˆ, Xىک 부ى‚¬ىˆک들ى€ X를 ë©کي† ë،œ ê°€ى§ˆ ىˆک ى—†ىٹµë‹ˆë‹¤.
그냥 Xىک 부ى‚¬ىˆک들ىک ى„œë¸Œيٹ¸ë¦¬ى—گى„œ, ىµœى پىک 답ى„ 구ي•´ ى „부 ëچ”ي•´ى£¼ë©´ ëگ©ë‹ˆë‹¤.
Xىک 부ى‚¬ىˆک를 C1, C2, C3, … ë¼ê³ ي•کë©´
dp[X][1] = dp[C1][0] + dp[C2][0] + dp[C3][0]…](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-30-320.jpg)
![I 대기ى—… ىٹ¹ë²”ى´ë„¤
ى¼€ى´ىٹ¤ 2 : Xê°€ Xىک ى‚¬ىˆکى™€ ë©کي† ë§پى„ ë§؛ى§€ ى•ٹى„ ë•Œ
ى¼€ى´ىٹ¤ 1ى—گى„œ ى¶”ê°€ë،œ, Xى™€ Xىک 부ى‚¬ىˆک ي•œëھ…ى´ ë©کي† ë§پ ي•کëٹ” ê²½ىڑ°ëڈ„ ê³ ë ¤ي•´ى•¼ ي•©ë‹ˆë‹¤.
dp[X][1] = max{
dp[C1][0] + dp[C2][0] + … // Xê°€ ى•„무ى™€ëڈ„ ë©کي† ë§پ ي•کى§€ ى•ٹىŒ
ى‹¤ë ¥[X]*ى‹¤ë ¥[C1] + dp[C1][1] + dp[C2][0] + … // Xى™€ C1ى´ ë©کي† ë§پى„ ë§؛ىŒ
ى‹¤ë ¥[X]*ى‹¤ë ¥[C2] + dp[C1][0] + dp[C2][1] + … // Xى™€ C1ى´ ë©کي† ë§پى„ ë§؛ىŒ
...](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-31-320.jpg)
![I 대기ى—… ىٹ¹ë²”ى´ë„¤
ى‹¤ë ¥[X]*ى‹¤ë ¥[C1] + dp[C1][1] + dp[C2][0] + … â‘
ى‹¤ë ¥[X]*ى‹¤ë ¥[C2] + dp[C1][0] + dp[C2][1] + … â‘،
…
ى„ ى „부 ى¼ى¼ى´ 구ي•کë©´, ى‹œê°„ى´ 너무 ىک¤ëک걸립니다. (ىگى‹ىک ىˆکê°€ Cë©´, O(Cآ²))
ë”°ë¼ى„œ (dp[C1][0] + dp[C2][0] + dp[C3][0]...)ى„ 미리 O(C)ë،œ 구ي•´ë†“ê³ ,
â‘ = (dp[C1][0] + dp[C2][0] + dp[C3][0]...) - dp[C1][0] + dp[C1][1] + ى‹¤ë ¥[X]*ى‹¤ë ¥[C1]
â‘، = (dp[C1][0] + dp[C2][0] + dp[C3][0]...) - dp[C2][0] + dp[C2][1] + ى‹¤ë ¥[X]*ى‹¤ë ¥[C2]
ë©´ ي•کë‚ک당 O(1)ى—گ 구ي• ىˆک ىˆىٹµë‹ˆë‹¤.](https://image.slidesharecdn.com/hongik-191105031605/85/2019-Open-Contest-32-320.jpg)