2hjsakhvchcvj hSKchvsABJChjSVCHjhvcvdxz.pptx
- 2. 2D Transformations ŌĆó What is transformations? ŌĆó The geometrical changes of an object from a current state to modified state. ŌĆó Why the transformations is needed? ŌĆó To manipulate the initially created object and to display the modified object without having to redraw it.
- 3. ŌĆó 2 ways ŌĆó Object Transformation ŌĆó Alter the coordinates descriptions an object ŌĆó Translation, rotation, scaling etc. ŌĆó Coordinate system unchanged ŌĆó Coordinate transformation ŌĆó Produce a different coordinate system 2D Transformations
- 4. Matrix Math ŌĆó Why do we use matrix? ŌĆó More convenient organization of data. ŌĆó More efficient processing ŌĆó Enable the combination of various concatenations ŌĆó Matrix addition and subtraction a b c d ’é▒ a ’é▒ c b ’é▒ d =
- 5. Translation ŌĆó A translation moves all points in an object along the same straight-line path to new positions. ŌĆó The path is represented by a vector, called the translation or shift vector. ŌĆó We can write the components: p'x = px + tx p'y = py + ty ŌĆó or in matrix form: P' = P + T tx ty xŌĆÖ yŌĆÖ x y tx ty = + (2, 2) = 6 =4 ?
- 6. Rotation ŌĆó A rotation repositions all points in an object along a circular path in the plane centered at the pivot point. ŌĆó First, weŌĆÖll assume the pivot is at the origin. ’ü▒ P PŌĆÖ
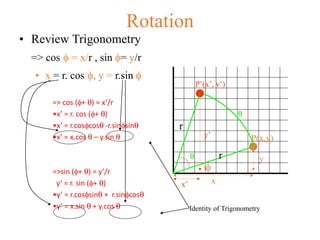
- 7. Rotation ŌĆó Review Trigonometry => cos ’ü” = x/r , sin ’ü”= y/r ŌĆó x = r. cos ’ü”, y = r.sin ’ü” ’ü▒ ’ü” P(x,y) x y r xŌĆÖ yŌĆÖ ’ü▒ PŌĆÖ(xŌĆÖ, yŌĆÖ) r => cos (’ü”+ ’ü▒) = xŌĆÖ/r ŌĆóxŌĆÖ = r. cos (’ü”+ ’ü▒) ŌĆóxŌĆÖ = r.cos’ü”cos’ü▒ -r.sin’ü”sin’ü▒ ŌĆóxŌĆÖ = x.cos ’ü▒ ŌĆō y.sin ’ü▒ =>sin (’ü”+ ’ü▒) = yŌĆÖ/r yŌĆÖ = r. sin (’ü”+ ’ü▒) ŌĆóyŌĆÖ = r.cos’ü”sin’ü▒ + r.sin’ü”cos’ü▒ ŌĆóyŌĆÖ = x.sin ’ü▒ + y.cos ’ü▒ Identity of Trigonometry
- 8. Rotation ŌĆó We can write the components: p'x = px cos ’ü▒ ŌĆō py sin ’ü▒ p'y = px sin ’ü▒ + py cos ’ü▒ ŌĆó or in matrix form: P' = R ŌĆó P ŌĆó ’ü▒ can be clockwise (-ve) or counterclockwise (+ve as our example). ŌĆó Rotation matrix ’ü▒ P(x,y) ’ü” x y r xŌĆÖ yŌĆÖ ’ü▒ PŌĆÖ(xŌĆÖ, yŌĆÖ) ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’ĆŁ ’ĆĮ ’ü▒ ’ü▒ ’ü▒ ’ü▒ cos sin sin cos R
- 9. ŌĆó Example ŌĆó Find the transformed point, PŌĆÖ, caused by rotating P= (5, 1) about the origin through an angle of 90’é░. Rotation ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’āŚ ’Ć½ ’āŚ ’āŚ ’ĆŁ ’āŚ ’ĆĮ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’éĘ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’ĆŁ ’ü▒ ’ü▒ ’ü▒ ’ü▒ ’ü▒ ’ü▒ ’ü▒ ’ü▒ cos sin sin cos cos sin sin cos y x y x y x ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’āŚ ’Ć½ ’āŚ ’āŚ ’ĆŁ ’āŚ ’ĆĮ 90 cos 1 90 sin 5 90 sin 1 90 cos 5 ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’āŚ ’Ć½ ’āŚ ’āŚ ’ĆŁ ’āŚ ’ĆĮ 0 1 1 5 1 1 0 5 ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā®’ĆŁ ’ĆĮ 5 1
- 10. Scaling ŌĆó Scaling changes the size of an object and involves two scale factors, Sx and Sy for the x- and y- coordinates respectively. ŌĆó Scales are about the origin. ŌĆó We can write the components: p'x = sx ŌĆó px p'y = sy ŌĆó py or in matrix form: P' = S ŌĆó P Scale matrix as: ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’ĆĮ y x s s S 0 0 P PŌĆÖ
- 11. Scaling ŌĆó If the scale factors are in between 0 and 1 ’ā© the points will be moved closer to the origin ’ā© the object will be smaller. P(2, 5) PŌĆÖ ŌĆó Example : ŌĆóP(2, 5), Sx = 0.5, Sy = 0.5 ŌĆóFind PŌĆÖ ?
- 12. Scaling ŌĆó If the scale factors are in between 0 and 1 ’ā© the points will be moved closer to the origin ’ā© the object will be smaller. P(2, 5) PŌĆÖ ŌĆó Example : ŌĆóP(2, 5), Sx = 0.5, Sy = 0.5 ŌĆóFind PŌĆÖ ? ŌĆóIf the scale factors are larger than 1 ’ā© the points will be moved away from the origin ’ā© the object will be larger. PŌĆÖ ŌĆó Example : ŌĆóP(2, 5), Sx = 2, Sy = 2 ŌĆóFind PŌĆÖ ?
- 13. Scaling ŌĆó If the scale factors are the same, Sx = Sy ’ā© uniform scaling ŌĆó Only change in size (as previous example) P(1, 2) PŌĆÖ ŌĆóIf Sx ’é╣ Sy ’ā© differential scaling. ŌĆóChange in size and shape ŌĆóExample : square ’āĀ rectangle ŌĆóP(1, 3), Sx = 2, Sy = 5 , PŌĆÖ ? What does scaling by 1 do? What is that matrix called? What does scaling by a negative value do?
- 14. Combining transformations We have a general transformation of a point: P' = M ŌĆó P + A When we scale or rotate, we set M, and A is the additive identity. When we translate, we set A, and M is the multiplicative identity. To combine multiple transformations, we must explicitly compute each transformed point. ItŌĆÖd be nicer if we could use the same matrix operation all the time. But weŌĆÖd have to combine multiplication and addition into a single operation.
- 15. Homogenous Coordinates ŌĆó LetŌĆÖs move our problem into 3D. ŌĆó Let point (x, y) in 2D be represented by point (x, y, 1) in the new space. ŌĆó Scaling our new point by any value a puts us somewhere along a particular line: (ax, ay, a). ŌĆó A point in 2D can be represented in many ways in the new space. ŌĆó (2, 4) ----------’āĀ (8, 16, 4) or (6, 12, 3) or (2, 4, 1) or etc. y y x x w ’ā©
- 16. Homogenous Coordinates ŌĆó We can always map back to the original 2D point by dividing by the last coordinate ŌĆó (15, 6, 3) ---’āĀ (5, 2). ŌĆó (60, 40, 10) -’āĀ ?. ŌĆó Why do we use 1 for the last coordinate? ŌĆó The fact that all the points along each line can be mapped back to the same point in 2D gives this coordinate system its name ŌĆō homogeneous coordinates.
- 17. Matrix Representation ŌĆó Point in column-vector: ŌĆó Our point now has three coordinates. So our matrix is needs to be 3x3. ŌĆó Translation x y 1 ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’éĘ ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’ĆĮ ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’éó ’éó 1 1 0 0 1 0 0 1 1 y x t t y x y x PŌĆ▓=T(tx,ty) . P
- 18. Rotation:
- 19. ŌĆó Rotation PŌĆ▓=R(╬ś). P ŌĆó Scaling Matrix Representation ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’éĘ ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’ĆŁ ’ĆĮ ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’éó ’éó 1 1 0 0 0 cos sin 0 sin cos 1 y x y x ’ü▒ ’ü▒ ’ü▒ ’ü▒ ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’éĘ ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’ĆĮ ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’éó ’éó 1 1 0 0 0 0 0 0 1 y x s s y x y x PŌĆ▓=S(sx, sy). P
- 21. Problem: Scaling