–¢–µ–º–∞ 3. –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó
- 1. –Æ.–ú–∞—Ä—á—É–∫ –ö—É—Ä—Å –ª–µ–∫—Ü—ñ–π –∑ –º–∞—Ç–µ–º–∞—Ç–∏–∫–∏ –°–ò–ù–£–°, –ö–û–°–ò–ù–£–°, –¢–ê–ù–ì–ï–ù–°, –ö–û–¢–ê–ù–ì–ï–ù–° –ö–£–¢–ê –ó –≥–µ–æ–º–µ—Ç—Ä—ñ—ó –≤—ñ–¥–æ–º–æ –æ—Å–Ω–æ–≤–Ω—ñ —Å–ø—ñ–≤–≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –≤ –ø—Ä—è–º–æ–∫—É—Ç–Ω–æ–º—É —Ç—Ä–∏–∫—É—Ç–Ω–∏–∫—É. –ü—Ä–∏–≥–∞–¥–∞—î–º–æ —ó—Ö. –Ý–æ–∑–≥–ª—è–Ω–µ–º–æ –∫–æ–ª–æ —Ä–∞–¥—ñ—É—Å–∞ R —É –ø—Ä—è–º–æ–∫—É—Ç–Ω—ñ–π —Å–∏—Å—Ç–µ–º—ñ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç. –ü–æ–ª–æ–∂–µ–Ω–Ω—è –¥–µ—è–∫–æ—ó —Ç–æ—á–∫–∏ –ê –∫–æ–ª–∞ –º–æ–∂–Ω–∞ –∑–∞–¥–∞—Ç–∏ —á–µ—Ä–µ–∑ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç–∏ —Ü—ñ—î—ó —Ç–æ—á–∫–∏, –∞–±–æ –∫—É—Ç–æ–º œÜ, –Ω–∞ —è–∫–∏–π –ø–æ–≤–µ—Ä–Ω–µ—Ç—å—Å—è —Ä–∞–¥—ñ—É—Å –∫–æ–ª–∞ –û–ê=R –≤—ñ–¥ –¥–µ—è–∫–æ–≥–æ –ø–æ—á–∞—Ç–∫–æ–≤–æ–≥–æ –ø–æ–ª–æ–∂–µ–Ω–Ω—è OR –¥–æ —Ç–æ—á–∫–∏ –ê. –í–∏–∫–æ—Ä–∏—Å—Ç–æ–≤—É—é—á–∏ —Å–ø—ñ–≤–≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è —É –ø—Ä—è–º–æ–∫—É—Ç–Ω–æ–º—É —Ç—Ä–∏–∫—É—Ç–Ω–∏–∫—É, –º–æ–∂–Ω–∞ –≤—Å—Ç–∞–Ω–æ–≤–∏—Ç–∏ –∑–≤'—è–∑–æ–∫ –º—ñ–∂ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç–∞–º–∏ —Ç–æ—á–∫–∏ –ê —ñ –∫—É—Ç–æ–º –ø–æ–≤–æ—Ä–æ—Ç—É —Ä–∞–¥—ñ—É—Å–∞ –∫–æ–ª–∞. –û–¥–µ—Ä–∂–∏–º–æ: R y =œïsin ; R x =œïcos ; x y tg =œï ; y x ctg =œï –°–∏–Ω—É—Å–æ–º –∫—É—Ç–∞ œÜ –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –æ—Ä–¥–∏–Ω–∞—Ç–∏ —Ç–æ—á–∫–∏ –ê(—Ö; —É) –∫–æ–ª–∞ –¥–æ —Ä–∞–¥—ñ—É—Å–∞ R —Ü—å–æ–≥–æ –∫–æ–ª–∞. –ö–æ—Å–∏–Ω—É—Å–æ–º –∫—É—Ç–∞ œÜ –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –∞–±—Å—Ü–∏—Å–∏ —Ç–æ—á–∫–∏ –ê(—Ö; —É) –∫–æ–ª–∞ –¥–æ —Ä–∞–¥—ñ—É—Å–∞ R —Ü—å–æ–≥–æ –∫–æ–ª–∞. –¢–∞–Ω–≥–µ–Ω—Å–æ–º –∫—É—Ç–∞ œÜ –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –æ—Ä–¥–∏–Ω–∞—Ç–∏ —Ç–æ—á–∫–∏ –ê(—Ö; —É) –∫–æ–ª–∞ –¥–æ –∞–±—Å—Ü–∏—Å–∏ —Ü—ñ—î—ó —Ç–æ—á–∫–∏. –ö–æ—Ç–∞–Ω–≥–µ–Ω—Å–æ–º –∫—É—Ç–∞ œÜ –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –∞–±—Å—Ü–∏—Å–∏ —Ç–æ—á–∫–∏ –ê(—Ö; —É) –∫–æ–ª–∞ –¥–æ –æ—Ä–¥–∏–Ω–∞—Ç–∏ —Ü—ñ—î—ó —Ç–æ—á–∫–∏. –ü–æ–Ω—è—Ç—Ç—è –≥—Ä–∞–¥—É—Å–∞: - –ö—É—Ç–æ–≤–∏–π –≥—Ä–∞–¥—É—Å ‚Äì —Ü–µ 180 1 —á–∞—Å—Ç–∏–Ω–∞ —Ä–æ–∑–≥–æ—Ä–Ω—É—Ç–æ–≥–æ –∫—É—Ç–∞; - –î—É–≥–æ–≤–∏–π –≥—Ä–∞–¥—É—Å ‚Äì —Ü–µ 180 1 —á–∞—Å—Ç–∏–Ω–∞ –¥—É–≥–∏ —Ä–æ–∑–≥–æ—Ä–Ω—É—Ç–æ–≥–æ –∫—É—Ç–∞. –ó–∞–≥–∞–ª—å–Ω–æ–ø—Ä–∏–π–Ω—è—Ç–∏–º —î –≤—ñ–¥–∫–ª–∞–¥–∞–Ω–Ω—è –¥–æ–¥–∞—Ç–Ω–∏—Ö –∫—É—Ç—ñ–≤ –ø—Ä–æ—Ç–∏ —Ö–æ–¥—É —Å—Ç—Ä—ñ–ª–∫–∏ –≥–æ–¥–∏–Ω–Ω–∏–∫–∞, –∞ –≤—ñ–¥'—î–º–Ω–∏—Ö ‚Äì –∑–∞ —Ö–æ–¥–æ–º –≥–æ–¥–∏–Ω–Ω–∏–∫–æ–≤–æ—ó —Å—Ç—Ä—ñ–ª–∫–∏. –Ý–∞–¥—ñ–∞–Ω–Ω–∞ –º—ñ—Ä–∞ –∫—É—Ç–∞ –ö—Ä—ñ–º –≥—Ä–∞–¥—É—Å–Ω–æ—ó –º—ñ—Ä–∏ –∫—É—Ç–∞ –≤ –º–∞—Ç–µ–º–∞—Ç–∏—Ü—ñ –≤–∏–∫–æ—Ä–∏—Å—Ç–æ–≤—É—é—Ç—å —â–µ –æ–¥–Ω—É –æ–¥–∏–Ω–∏—Ü—é –≤–∏–º—ñ—Ä—é–≤–∞–Ω–Ω—è –∫—É—Ç–∞ ‚Äì —Ä–∞–¥—ñ–∞–Ω. –Ý–æ–∑–≥–ª—è–Ω–µ–º–æ –¥–≤–∞ –∫–æ–Ω—Ü–µ–Ω—Ç—Ä–∏—á–Ω–∏—Ö –∫–æ–ª–∞ –∑ —Ä–∞–¥—ñ—É—Å–∞–º–∏ R1 —ñ R2 —Ç–∞ –¥–≤–∞ —Ü–µ–Ω—Ç—Ä–∞–ª—å–Ω—ñ –∫—É—Ç–∏ Œ± —ñ Œ≤ (Œ± < Œ≤). –í—Å—Ç–∞–Ω–æ–≤–ª–µ–Ω–æ, —â–æ –¥–ª—è –æ–¥–Ω–æ–≥–æ —ñ —Ç–æ–≥–æ –∂ —Ü–µ–Ω—Ç—Ä–∞–ª—å–Ω–æ–≥–æ –∫—É—Ç–∞ –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –¥—É–≥ –∫–æ–Ω—Ü–µ–Ω—Ç—Ä–∏—á–Ω–∏—Ö –∫—ñ–ª –¥–æ —ó—Ö —Ä–∞–¥—ñ—É—Å—ñ–≤ —î –≤–µ–ª–∏—á–∏–Ω–æ—é —Å—Ç–∞–ª–æ—é. –¶–µ –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –∑–∞–ª–µ–∂–∏—Ç—å —Ç—ñ–ª—å–∫–∏ –≤—ñ–¥ –≤–µ–ª–∏—á–∏–Ω–∏ –∫—É—Ç–∞. –û—Ç–∂–µ, n R l R l == 2 2 1 1 —ñ m R l R l == 2 ' 2 1 ' 1 –Ø–∫—â–æ Œ± < Œ≤, —Ç–æ n < m. –î–∞–Ω–µ –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –≤–∑—è—Ç–æ –∑–∞ –º—ñ—Ä—É –∫—É—Ç–∞: a R l = , –¥–µ –∞ ‚Äì —á–∏—Å–ª–æ. –ß–∏—Å–ª–æ –∞ —Ö–∞—Ä–∞–∫—Ç–µ—Ä–∏–∑—É—î –≤–µ–ª–∏—á–∏–Ω—É –¥–∞–Ω–æ–≥–æ —Ü–µ–Ω—Ç—Ä–∞–ª—å–Ω–æ–≥–æ –∫—É—Ç–∞. –í —Ä–∞–¥—ñ–∞–Ω–Ω—ñ–π —Å–∏—Å—Ç–µ–º—ñ –∑–∞ –æ–¥–∏–Ω–∏—Ü—é –≤–∏–º—ñ—Ä—é–≤–∞–Ω–Ω—è –∫—É—Ç—ñ–≤ —ñ –¥—É–≥ –≤–∑—è—Ç–æ –≤–µ–ª–∏—á–∏–Ω—É —Ü–µ–Ω—Ç—Ä–∞–ª—å–Ω–æ–≥–æ –∫—É—Ç–∞, –¥–ª—è —è–∫–æ–≥–æ –¥–æ–≤–∂–∏–Ω–∞ –≤—ñ–¥–ø–æ–≤—ñ–¥–Ω–æ—ó –¥—É–≥–∏ –¥–æ—Ä—ñ–≤–Ω—é—î –¥–æ–≤–∂–∏–Ω—ñ —Ä–∞–¥—ñ—É—Å–∞. c b=œïsin c a=œïcos a btg =œï b actg =œï
- 2. –¢–µ–º–∞: –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó –ü—Ä–∏ l = R a = 1 —Ä–∞–¥ (—Ä–∞–¥—ñ–∞–Ω) –ì—Ä–∞–¥—É—Å–Ω–∞ –º—ñ—Ä–∞ —Ä–æ–∑–≥–æ—Ä–Ω—É—Ç–æ–≥–æ –∫—É—Ç–∞ ‚Äì 180–æ . –Ý–∞–¥—ñ–∞–Ω–Ω–∞ –º—ñ—Ä–∞ —Ä–æ–∑–≥–æ—Ä–Ω—É—Ç–æ–≥–æ –∫—É—Ç–∞ ‚Äì œÄ —Ä–∞–¥. –ü–µ—Ä–µ—Ö—ñ–¥ –≤—ñ–¥ –≥—Ä–∞–¥—É—Å–Ω–æ—ó –º—ñ—Ä–∏ –∫—É—Ç–∞ –¥–æ —Ä–∞–¥—ñ–∞–Ω–Ω–æ—ó: o o a Œ± œÄ ‚ãÖ= 180 . –ü–µ—Ä–µ—Ö—ñ–¥ –≤—ñ–¥ —Ä–∞–¥—ñ–∞–Ω–Ω–æ—ó –º—ñ—Ä–∏ –∫—É—Ç–∞ –¥–æ –≥—Ä–∞–¥—É—Å–Ω–æ—ó: a o o ‚ãÖ= œÄ Œ± 180 . –¢–Ý–ò–ì–û–ù–û–ú–ï–¢–Ý–ò–ß–ù–Ü –§–£–ù–ö–¶–Ü–á –ß–ò–°–õ–û–í–û–ì–û –ê–Ý–ì–£–ú–ï–ù–¢–£ –Ý–æ–∑–≥–ª—è–Ω–µ–º–æ –æ–¥–∏–Ω–∏—á–Ω–µ –∫–æ–ª–æ (R=1) —É —Å–∏—Å—Ç–µ–º—ñ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç. –ü–æ–∑–Ω–∞—á–∏–º–æ –Ω–∞ —Ü—å–æ–º—É –∫–æ–ª—ñ —Ç–æ—á–∫–∏ –Ý, –ø–æ–ª–æ–∂–µ–Ω–Ω—è —è–∫–∏—Ö –≤–∏–∑–Ω–∞—á–∞—î—Ç—å—Å—è –∫—É—Ç–∞–º–∏ 0 —Ä–∞–¥ (0–æ ), 6 œÄ —Ä–∞–¥ (30–æ ), 4 œÄ —Ä–∞–¥ (45–æ ), 3 œÄ —Ä–∞–¥ (60–æ ), 2 œÄ —Ä–∞–¥ (90–æ ). –ü—Ä–∏ –ø–æ–±—É–¥–æ–≤—ñ —Ç–æ—á–æ–∫ –¥—É–≥—É –∫–æ–ª–∞ –¥—ñ–ª–∏–º–æ –Ω–∞ –≤—ñ–¥–ø–æ–≤—ñ–¥–Ω—É –∫—ñ–ª—å–∫—ñ—Å—Ç—å —Ä—ñ–≤–Ω–∏—Ö —á–∞—Å—Ç–∏–Ω. –ó–≤–µ—Ä–Ω—ñ—Ç—å —É–≤–∞–≥—É, —â–æ –∫–æ–∂–Ω–æ–º—É –∑ —Ü–∏—Ö –∫—É—Ç—ñ–≤ –≤—ñ–¥–ø–æ–≤—ñ–¥–∞—î –ø–µ–≤–Ω–∞ –¥—É–≥–∞ –æ–¥–∏–Ω–∏—á–Ω–æ–≥–æ –∫–æ–ª–∞. –ü—Ä–∏ R = 1 –∞ = l (–≤–µ–ª–∏—á–∏–Ω–∞ –∫—É—Ç–∞ –¥–æ—Ä—ñ–≤–Ω—é—î –≤—ñ–¥–ø–æ–≤—ñ–¥–Ω—ñ–π –¥—É–∑—ñ –æ–¥–∏–Ω–∏—á–Ω–æ–≥–æ –∫–æ–ª–∞). –û—Ç–∂–µ, –∫–æ–∂–Ω–æ–º—É –¥—ñ–π—Å–Ω–æ–º—É —á–∏—Å–ª—É –∞ –Ω–∞ –æ–¥–∏–Ω–∏—á–Ω–æ–º—É –∫–æ–ª—ñ –≤—ñ–¥–ø–æ–≤—ñ–¥–∞—î –ø–µ–≤–Ω–∞ —Ç–æ—á–∫–∞, –ø–æ–ª–æ–∂–µ–Ω–Ω—è —è–∫–æ—ó –≤–∏–∑–Ω–∞—á–∞—î—Ç—å—Å—è –≤—ñ–¥–ø–æ–≤—ñ–¥–Ω–æ—é –∞–±—Å—Ü–∏—Å–æ—é —ñ –æ—Ä–¥–∏–Ω–∞—Ç–æ—é. –¢–∞–∫–∏–º —á–∏–Ω–æ–º, –º—ñ–∂ –¥—ñ–π—Å–Ω–∏–º —á–∏—Å–ª–æ–º –∞ —ñ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç–∞–º–∏ —Ç–æ—á–∫–∏ –æ–¥–∏–Ω–∏—á–Ω–æ–≥–æ –∫–æ–ª–∞ —ñ—Å–Ω—É—î –∑–∞–ª–µ–∂–Ω—ñ—Å—Ç—å(–≤—ñ–¥–ø–æ–≤—ñ–¥–Ω—ñ—Å—Ç—å), —è–∫—É –Ω–∞–∑–≤–∞–ª–∏ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–æ—é —Ñ—É–Ω–∫—Ü—ñ—î—é —á–∏—Å–ª–æ–≤–æ–≥–æ –∞—Ä–≥—É–º–µ–Ω—Ç—É. –°–∏–Ω—É—Å–æ–º —á–∏—Å–ª–∞ –∞ –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –æ—Ä–¥–∏–Ω–∞—Ç–∞ —Ç–æ—á–∫–∏ –Ý –æ–¥–∏–Ω–∏—á–Ω–æ–≥–æ –∫–æ–ª–∞, –≤ —è–∫—É –ø–µ—Ä–µ—Ö–æ–¥–∏—Ç—å –ø–æ—á–∞—Ç–∫–æ–≤–∞ —Ç–æ—á–∫–∞ –Ý–æ(1; 0) –ø—Ä–∏ –ø–æ–≤–æ—Ä–æ—Ç—ñ –Ω–∞–≤–∫–æ–ª–æ —Ü–µ–Ω—Ç—Ä–∞ –∫–æ–ª–∞ –Ω–∞ –∫—É—Ç –∞ —Ä–∞–¥—ñ–∞–Ω. sin a = y –ö–æ—Å–∏–Ω—É—Å–æ–º —á–∏—Å–ª–∞ –∞ –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –∞–±—Å—Ü–∏—Å–∞ —Ç–æ—á–∫–∏ –Ý –æ–¥–∏–Ω–∏—á–Ω–æ–≥–æ –∫–æ–ª–∞, –≤ —è–∫—É –ø–µ—Ä–µ—Ö–æ–¥–∏—Ç—å –ø–æ—á–∞—Ç–∫–æ–≤–∞ —Ç–æ—á–∫–∞ –Ý–æ(1; 0) –ø—Ä–∏ –ø–æ–≤–æ—Ä–æ—Ç—ñ –Ω–∞–≤–∫–æ–ª–æ —Ü–µ–Ω—Ç—Ä–∞ –∫–æ–ª–∞ –Ω–∞ –∫—É—Ç –∞ —Ä–∞–¥—ñ–∞–Ω. cos a = x –¢–∞–Ω–≥–µ–Ω—Å–æ–º —á–∏—Å–ª–∞ –∞ –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è a a cos sin . a a a cos sin tg = –ö–æ—Ç–∞–Ω–≥–µ–Ω—Å–æ–º —á–∏—Å–ª–∞ –∞ –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è a a sin cos . a a a sin cos ctg = –ó–Ω–∞–∫–∏ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π –°–∏–Ω—É—Å –ö–æ—Å–∏–Ω—É—Å –¢–∞–Ω–≥–µ–Ω—Å, –∫–æ—Ç–∞–Ω–≥–µ–Ω—Å
- 3. –Æ.–ú–∞—Ä—á—É–∫ –ö—É—Ä—Å –ª–µ–∫—Ü—ñ–π –∑ –º–∞—Ç–µ–º–∞—Ç–∏–∫–∏ –û–°–ù–û–í–ù–Ü –°–ü–Ü–í–í–Ü–î–ù–û–®–ï–ù–ù–Ø –ú–Ü–ñ –¢–Ý–ò–ì–û–ù–û–ú–ï–¢–Ý–ò–ß–ù–ò–ú–ò –§–£–ù–ö–¶–Ü–Ø–ú–ò –û–î–ù–û–ì–û –ê–Ý–ì–£–ú–ï–ù–¢–£ –û—Å–Ω–æ–≤–Ω–∞ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∞ —Ç–æ—Ç–æ–∂–Ω—ñ—Å—Ç—å: sin2 Œ± + cos2 Œ± = 1 –°–ø—ñ–≤–≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –º—ñ–∂ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏–º–∏ —Ñ—É–Ω–∫—Ü—ñ—è–º–∏ –æ–¥–Ω–æ–≥–æ –∞—Ä–≥—É–º–µ–Ω—Ç—É: Œ± Œ± Œ± cos sin =tg , cos Œ± ‚âÝ 0 Œ± Œ± Œ± sin cos =ctg , sin Œ± ‚âÝ 0 1=‚ãÖ Œ±Œ± ctgtg Œ± Œ± tg ctg 1 = Œ± Œ± ctg tg 1 = Œ± Œ± 2 2 cos 1 1 =+ tg Œ± Œ± 2 sin 1 1 =+ ctg –§–û–Ý–ú–£–õ–ò –ó–í–ï–î–ï–ù–ù–Ø –§–æ—Ä–º—É–ª–∏ –∑–≤–µ–¥–µ–Ω–Ω—è ‚Äì —Ü–µ —Ñ–æ—Ä–º—É–ª–∏ –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π –∫—É—Ç—ñ–≤ (90–æ ¬± Œ±), (180–æ ¬± Œ±), (270–æ ¬± Œ±), (360–æ ¬± Œ±) —É —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó –≥–æ—Å—Ç—Ä–æ–≥–æ –∫—É—Ç–∞ Œ±. –ü—Ä–∞–≤–∏–ª–æ –∑–≤–µ–¥–µ–Ω–Ω—è: - –£ –ø—Ä–∞–≤—ñ–π —á–∞—Å—Ç–∏–Ω—ñ —Ä—ñ–≤–Ω–æ—Å—Ç—ñ —Å—Ç–∞–≤–∏—Ç—å—Å—è —Ç–æ–π –∑–Ω–∞–∫, —è–∫–∏–π –º–∞—î —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∞ —Ñ—É–Ω–∫—Ü—ñ—è, —â–æ –∑–≤–æ–¥–∏—Ç—å—Å—è; - –ü—Ä–∏ –∑–≤–µ–¥–µ–Ω–Ω—ñ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π –∫—É—Ç—ñ–≤ (180–æ ¬± Œ±), (360–æ ¬± Œ±) —ó—Ö –Ω–∞–∑–≤–∏ –Ω–µ –∑–º—ñ–Ω—é—é—Ç—å—Å—è, –∞ –∫—É—Ç—ñ–≤ (90–æ ¬± Œ±), (270–æ ¬± Œ±) –Ω–∞–∑–≤–∏ —Ñ—É–Ω–∫—Ü—ñ–π –∑–º—ñ–Ω—é—é—Ç—å—Å—è: —Å–∏–Ω—É—Å –Ω–∞ –∫–æ—Å–∏–Ω—É—Å, –∫–æ—Å–∏–Ω—É—Å –Ω–∞ —Å–∏–Ω—É—Å, —Ç–∞–Ω–≥–µ–Ω—Å –Ω–∞ –∫–æ—Ç–∞–Ω–≥–µ–Ω—Å, –∫–æ—Ç–∞–Ω–≥–µ–Ω—Å –Ω–∞ —Ç–∞–Ω–≥–µ–Ω—Å. –§–æ—Ä–º—É–ª–∏ –∑–≤–µ–¥–µ–Ω–Ω—è sin (90–æ ‚Äì Œ±) = cos Œ± sin (90–æ + Œ±) = cos Œ± cos (90–æ ‚Äì Œ±) = sin Œ± cos (90–æ + Œ±) = ‚Äìsin Œ± tg (90–æ ‚Äì Œ±) = ctg Œ± tg (90–æ + Œ±) = ‚Äìctg Œ± ctg (90–æ ‚Äì Œ±) = tg Œ± ctg (90–æ + Œ±) = ‚Äìtg Œ± sin (180–æ ‚Äì Œ±) = sin Œ± sin (180–æ + Œ±) = ‚Äìsin Œ± cos (180–æ ‚Äì Œ±) = ‚Äìcos Œ± cos (180–æ + Œ±) = ‚Äìcos Œ± tg (180–æ ‚Äì Œ±) = ‚Äìtg Œ± tg (180–æ + Œ±) = tg Œ± ctg (180–æ ‚Äì Œ±) = ‚Äìctg Œ± ctg (180–æ + Œ±) = ctg Œ± sin (270–æ ‚Äì Œ±) = ‚Äìcos Œ± sin (270–æ + Œ±) = ‚Äìcos Œ± cos (270–æ ‚Äì Œ±) = ‚Äìsin Œ± cos (270–æ + Œ±) = sin Œ± tg (270–æ ‚Äì Œ±) = ctg Œ± tg (270–æ + Œ±) = ‚Äìctg Œ± ctg (270–æ ‚Äì Œ±) = tg Œ± ctg (270–æ + Œ±) = ‚Äìtg Œ± sin (360–æ ‚Äì Œ±) = ‚Äìsin Œ± sin (360–æ + Œ±) = sin Œ± cos (360–æ ‚Äì Œ±) = cos Œ± cos (360–æ + Œ±) = cos Œ± tg (360–æ ‚Äì Œ±) = ‚Äìtg Œ± tg (360–æ + Œ±) = tg Œ± ctg (360–æ ‚Äì Œ±) = ‚Äìctg Œ± ctg (360–æ + Œ±) = ctg Œ± –ü–ï–Ý–Ü–û–î–ò–ß–ù–Ü–°–¢–¨ –§–£–ù–ö–¶–Ü–ô –§—É–Ω–∫—Ü—ñ—è y = f(x) –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –ø–µ—Ä—ñ–æ–¥–∏—á–Ω–æ—é –∑ –ø–µ—Ä—ñ–æ–¥–æ–º –¢ ‚âÝ 0, —è–∫—â–æ –¥–ª—è –±—É–¥—å-—è–∫–æ–≥–æ —Ö –∑ –æ–±–ª–∞—Å—Ç—ñ –≤–∏–∑–Ω–∞—á–µ–Ω–Ω—è —Ñ—É–Ω–∫—Ü—ñ—ó —á–∏—Å–ª–∞ —Ö + –¢ —ñ —Ö ‚Äì –¢ —Ç–∞–∫–æ–∂ –Ω–∞–ª–µ–∂–∞—Ç—å –æ–±–ª–∞—Å—Ç—ñ –≤–∏–∑–Ω–∞—á–µ–Ω–Ω—è —ñ –≤–∏–∫–æ–Ω—É—î—Ç—å—Å—è —É–º–æ–≤–∞ f (x) = f(x ‚Äì T) = f(x + T) –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó —î –ø–µ—Ä—ñ–æ–¥–∏—á–Ω–∏–º–∏. –ù–∞–π–º–µ–Ω—à–∏–º –¥–æ–¥–∞—Ç–Ω–∏–º –ø–µ—Ä—ñ–æ–¥–æ–º —Å–∏–Ω—É—Å–∞ —ñ –∫–æ—Å–∏–Ω—É—Å–∞ —î —á–∏—Å–ª–æ 2œÄ, –∞ —Ç–∞–Ω–≥–µ–Ω—Å–∞ —ñ –∫–æ—Ç–∞–Ω–≥–µ–Ω—Å–∞ ‚Äì —á–∏—Å–ª–æ œÄ. –û—Ç–∂–µ,
- 4. –¢–µ–º–∞: –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó sin(Œ± + 2œÄk) = sin Œ±, k œµ Z cos(Œ± + 2œÄk) = cos Œ±, k œµ Z tg(Œ± + œÄk) = tg Œ±, k œµ Z ctg(Œ± + œÄk) = ctg Œ±, k œµ Z –ü—Ä–∏–∫–ª–∞–¥ –≤–∏–∑–Ω–∞—á–µ–Ω–Ω—è –ø–µ—Ä—ñ–æ–¥—É —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–æ—ó —Ñ—É–Ω–∫—Ü—ñ—ó, –∑–∞–¥–∞–Ω–æ—ó —Ñ–æ—Ä–º—É–ª–æ—é y = sin(kx + b) —ñ y = tg(kx + b). –î–ª—è ( ) k Tbkxy œÄ2 sin =‚áí+= ( ) k Tbkxtgy œÄ =‚áí+= –í–õ–ê–°–¢–ò–í–û–°–¢–Ü –¢–ê –ì–Ý–ê–§–Ü–ö–ò –¢–Ý–ò–ì–û–ù–û–ú–ï–¢–Ý–ò–ß–ù–ò–• –§–£–ù–ö–¶–Ü–ô –ü—Ä–∏ –ø–æ–±—É–¥–æ–≤—ñ –≥—Ä–∞—Ñ—ñ–∫—ñ–≤ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π —Ç–∞ –ø—Ä–∏ –¥–æ—Å–ª—ñ–¥–∂–µ–Ω–Ω—ñ —Ü–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π –≤–∞–∂–ª–∏–≤—É —Ä–æ–ª—å –≤—ñ–¥—ñ–≥—Ä–∞—î –ø–µ—Ä—ñ–æ–¥ —Ñ—É–Ω–∫—Ü—ñ–π. –ö—Ä—ñ–º —Ç–æ–≥–æ, –¥–æ –ø–æ–Ω—è—Ç—Ç—è –ø–µ—Ä—ñ–æ–¥—É –ø—Ä–∏–≤–æ–¥—è—Ç—å –ø–µ—Ä—ñ–æ–¥–∏—á–Ω—ñ –ø—Ä–æ—Ü–µ—Å–∏, —è–∫—ñ –≤—ñ–¥–±—É–≤–∞—é—Ç—å—Å—è –≤ –∞—Å—Ç—Ä–æ–Ω–æ–º—ñ—ó, —Ç–µ—Ö–Ω—ñ—Ü—ñ, –ø—Ä–∏—Ä–æ–¥—ñ. –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó –≤–∏–∫–æ—Ä–∏—Å—Ç–æ–≤—É—é—Ç—å—Å—è –¥–æ –º–æ–¥–µ–ª—é–≤–∞–Ω–Ω—è –∑–∞–∫–æ–Ω–æ–º—ñ—Ä–Ω–æ—Å—Ç–µ–π –∫–æ–ª–∏–≤–∞–ª—å–Ω–æ–≥–æ —Ä—É—Ö—É, –∞ —Å–∞–º–µ –º–æ–¥–µ–ª—é–≤–∞–Ω–Ω—è —Ä—ñ–≤–Ω–æ–º—ñ—Ä–Ω–æ–≥–æ –æ–±–µ—Ä—Ç–∞–ª—å–Ω–æ–≥–æ —Ä—É—Ö—É. –°–∞–º–µ –∑ —Ü–∏–º –ø–æ—Ö–æ–¥–∂–µ–Ω–Ω—è–º —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π –ø–æ–≤‚Ä≤—è–∑–∞–Ω–∞ –æ–¥–Ω–∞ –∑ –≥–æ–ª–æ–≤–Ω–∏—Ö —ó—Ö –æ—Å–æ–±–ª–∏–≤–æ—Å—Ç–µ–π ‚Äì –ø–µ—Ä—ñ–æ–¥–∏—á–Ω—ñ—Å—Ç—å. –í–∏–≤—á–µ–Ω–Ω—è —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π —Ä–æ–∑–ø–æ—á–Ω–µ–º–æ –∑ –ø–æ–±—É–¥–æ–≤–∏ –≥—Ä–∞—Ñ—ñ–∫–∞ —Ñ—É–Ω–∫—Ü—ñ—ó, –∞ –ø–æ—Ç—ñ–º ¬´—á–∏—Ç–∞—é—á–∏¬ª –≥—Ä–∞—Ñ—ñ–∫, –≤–∏–∑–Ω–∞—á–∏–º–æ —ñ –∑–∞–ø–∏—à–µ–º–æ –≤–ª–∞—Å—Ç–∏–≤–æ—Å—Ç—ñ —Ñ—É–Ω–∫—Ü—ñ—ó. –ü–æ–±—É–¥—É–≤–∞—Ç–∏ –≥—Ä–∞—Ñ—ñ–∫ –±—É–¥—å-—è–∫–æ—ó —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–æ—ó —Ñ—É–Ω–∫—Ü—ñ—ó –º–æ–∂–Ω–∞ –¥–≤–æ–º–∞ —Å–ø–æ—Å–æ–±–∞–º–∏: –≥–µ–æ–º–µ—Ç—Ä–∏—á–Ω–∏–º —ñ –∞–Ω–∞–ª—ñ—Ç–∏—á–Ω–∏–º. –ì–µ–æ–º–µ—Ç—Ä–∏—á–Ω–∏–π —Å–ø–æ—Å—ñ–± –ø–æ–±—É–¥–æ–≤–∏ –æ–ø–∏—Å–∞–Ω–æ —É –ø—ñ–¥—Ä—É—á–Ω–∏–∫—É. / –®–∫—ñ–ª—å –ú.–Ü. —Ç–∞ —ñ–Ω.., –ê–ª–≥–µ–±—Ä–∞ —ñ –ø–æ—á–∞—Ç–∫–∏ –∞–Ω–∞–ª—ñ–∑—É, 10 ‚Äì 11 –∫–ª., ¬ß6 —Å.38 ‚Äì 39 / –ü–æ–±—É–¥—É—î–º–æ –≥—Ä–∞—Ñ—ñ–∫ —Ñ—É–Ω–∫—Ü—ñ—ó y = sin x –∞–Ω–∞–ª—ñ—Ç–∏—á–Ω–∏–º —Å–ø–æ—Å–æ–±–æ–º. –û—Å–∫—ñ–ª—å–∫–∏ –Ω–∞–π–º–µ–Ω—à–∏–º –¥–æ–¥–∞—Ç–Ω–∏–º –ø–µ—Ä—ñ–æ–¥–æ–º —Ñ—É–Ω–∫—Ü—ñ—ó —î —á–∏—Å–ª–æ 2œÄ, —Ç–æ –ø–æ–±—É–¥—É—î–º–æ –≥—Ä–∞—Ñ—ñ–∫ –ª–∏—à–µ –Ω–∞ –ø—Ä–æ–º—ñ–∂–∫—É [-œÄ; œÄ]. —Ö -œÄ -3œÄ/4 -œÄ/2 -œÄ/4 0 œÄ/4 œÄ/2 3œÄ/4 œÄ —É 0 - 2 2 -1 - 2 2 0 2 2 1 2 2 0 –ü–æ–±—É–¥–æ–≤–∞ –≥—Ä–∞—Ñ—ñ–∫–∞ —Ñ—É–Ω–∫—Ü—ñ—ó. –ì—Ä–∞—Ñ—ñ–∫ —Ñ—É–Ω–∫—Ü—ñ—ó y = sin x –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è —Å–∏–Ω—É—Å–æ—ó–¥–æ—é. –û—Å–∫—ñ–ª—å–∫–∏ —Ñ—É–Ω–∫—Ü—ñ—è y = sin x –ø–µ—Ä—ñ–æ–¥–∏—á–Ω–∞ –∑ –ø–µ—Ä—ñ–æ–¥–æ–º 2œÄ–ø, –ø‚ààZ, —Ç–æ –≥—Ä–∞—Ñ—ñ–∫ —Ñ—É–Ω–∫—Ü—ñ—ó –º–æ–∂–Ω–∞ –ø—Ä–æ–¥–æ–≤–∂–∏—Ç–∏ –≤—ñ–¥–ø–æ–≤—ñ–¥–Ω–∏–º –ø–∞—Ä–∞–ª–µ–ª—å–Ω–∏–º –ø–µ—Ä–µ–Ω–µ—Å–µ–Ω–Ω—è–º –≥—Ä–∞—Ñ—ñ–∫–∞ y = sin x.
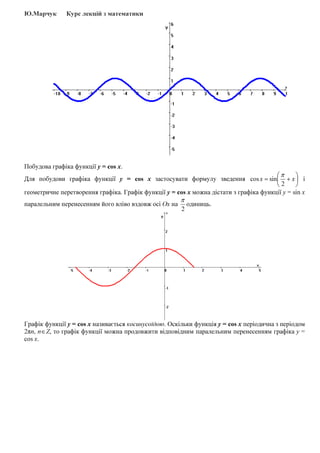
- 5. Ю.Марчук Курс лекцій з математики Побудова графіка функції y = cos x. Для побудови графіка функції y = cos x застосувати формулу зведення       += xx 2 sincos π і геометричне перетворення графіка. Графік функції y = cos x можна дістати з графіка функції y = sin x паралельним перенесенням його вліво вздовж осі Ох на 2 π одиниць. Графік функції y = cos x називається косинусоїдою. Оскільки функція y = cos x періодична з періодом 2πп, п∈Z, то графік функції можна продовжити відповідним паралельним перенесенням графіка y = cos x.
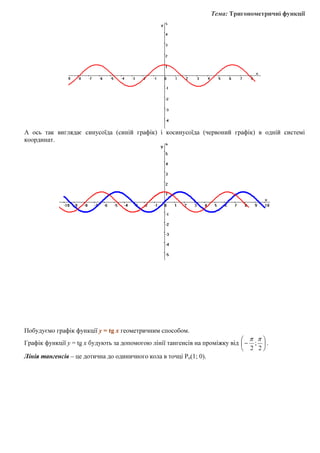
- 6. –¢–µ–º–∞: –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó –ê –æ—Å—å —Ç–∞–∫ –≤–∏–≥–ª—è–¥–∞—î —Å–∏–Ω—É—Å–æ—ó–¥–∞ (—Å–∏–Ω—ñ–π –≥—Ä–∞—Ñ—ñ–∫) —ñ –∫–æ—Å–∏–Ω—É—Å–æ—ó–¥–∞ (—á–µ—Ä–≤–æ–Ω–∏–π –≥—Ä–∞—Ñ—ñ–∫) –≤ –æ–¥–Ω—ñ–π —Å–∏—Å—Ç–µ–º—ñ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç. –ü–æ–±—É–¥—É—î–º–æ –≥—Ä–∞—Ñ—ñ–∫ —Ñ—É–Ω–∫—Ü—ñ—ó y = tg x –≥–µ–æ–º–µ—Ç—Ä–∏—á–Ω–∏–º —Å–ø–æ—Å–æ–±–æ–º. –ì—Ä–∞—Ñ—ñ–∫ —Ñ—É–Ω–∫—Ü—ñ—ó y = tg x –±—É–¥—É—é—Ç—å –∑–∞ –¥–æ–ø–æ–º–æ–≥–æ—é –ª—ñ–Ω—ñ—ó —Ç–∞–Ω–≥–µ–Ω—Å—ñ–≤ –Ω–∞ –ø—Ä–æ–º—ñ–∂–∫—É –≤—ñ–¥ Ô£∑ Ô£∏ Ô£∂ Ô£¨ Ô£≠ Ô£´ ‚àí 2 ; 2 œÄœÄ . –õ—ñ–Ω—ñ—è —Ç–∞–Ω–≥–µ–Ω—Å—ñ–≤ ‚Äì —Ü–µ –¥–æ—Ç–∏—á–Ω–∞ –¥–æ –æ–¥–∏–Ω–∏—á–Ω–æ–≥–æ –∫–æ–ª–∞ –≤ —Ç–æ—á—Ü—ñ –Ý–æ(1; 0).
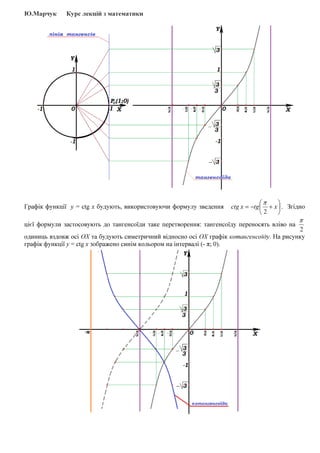
- 7. Ю.Марчук Курс лекцій з математики Графік функції y = сtg x будують, використовуючи формулу зведення       +−= xtgxctg 2 π . Згідно цієї формули застосовують до тангенсоїди таке перетворення: тангенсоїду переносять вліво на 2 π одиниць вздовж осі ОХ та будують симетричний відносно осі ОХ графік котангенсоїду. На рисунку графік функції y = сtg x зображено синім кольором на інтервалі (- π; 0).
- 8. –¢–µ–º–∞: –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó –í–ª–∞—Å—Ç–∏–≤–æ—Å—Ç—ñ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π –§—É–Ω–∫—Ü—ñ—è –í–ª–∞—Å—Ç–∏–≤—ñ—Å—Ç—å y = sin x y = cos x y = tg x y = ctg x 1.–û–±–ª–∞—Å—Ç—å –≤–∏–∑–Ω–∞—á–µ–Ω–Ω—è D(y) ‚àà R D(y) ‚àà R D(y) ‚àà R, x ‚âÝ œÄ/2 + œÄ¬∑n D(y) ‚àà R, x ‚âÝ œÄ¬∑n 2.–û–±–ª–∞—Å—Ç—å –∑–Ω–∞—á–µ–Ω—å E(y) ‚àà [-1; 1 ] E(y) ‚àà [-1; 1 ] E(y) ‚àà R E(y) ‚àà R 3.–ü–∞—Ä–Ω—ñ—Å—Ç—å (–Ω–µ–ø–∞—Ä–Ω—ñ—Å—Ç—å) –ù –µ –ø –∞ —Ä –Ω –∞ –ü –∞ —Ä –Ω –∞ –ù –µ –ø –∞ —Ä –Ω –∞ –ù –µ –ø –∞ —Ä –Ω –∞ 4.–ü–µ—Ä—ñ–æ–¥–∏—á–Ω—ñ—Å—Ç—å T = 2œÄn, n ‚àà Z T = 2œÄn, n ‚àà Z T = œÄn, n ‚àà Z T = œÄn, n ‚àà Z 5.–ù–∞–±—É–≤–∞—î –Ω—É–ª—å–æ–≤–∏—Ö –∑–Ω–∞—á–µ–Ω—å sin x = 0, –ø—Ä–∏ x = œÄn, n ‚àà Z cos x = 0, –ø—Ä–∏ x = œÄ/2 + œÄn, n‚ààZ tg x = 0, –ø—Ä–∏ x = œÄn, n ‚àà Z ctg x = 0, –ø—Ä–∏ x = œÄ/2 + œÄn, n‚ààZ 6.–ü—Ä–æ–º—ñ–∂–∫–∏ –∑—Ä–æ—Å—Ç–∞–Ω–Ω—è [ - œÄ/2 + 2œÄn; œÄ/2 + 2œÄn ] [ - œÄ + 2œÄn; 0 + 2œÄn ] [ - œÄ/2 + œÄn; œÄ/2 + œÄn ] –ù –µ –º –∞ —î 7.–ü—Ä–æ–º—ñ–∂–∫–∏ —Å–ø–∞–¥–∞–Ω–Ω—è [ œÄ/2 + 2œÄn; 3œÄ/2 + 2œÄn ] [ 0 + 2œÄn; œÄ + 2œÄn ] –ù –µ –º –∞ —î [ 0 + œÄn; œÄ + 2œÄn ] 8.–ù–∞–±—É–≤–∞—î –¥–æ–¥–∞—Ç–Ω–∏—Ö –∑–Ω–∞—á–µ–Ω—å sin x > 0, ( 2œÄn; œÄ + 2œÄn) cos x > 0, ( - œÄ/2 + 2œÄn; œÄ/2 + 2œÄn ) tg x > 0, ( 0 + œÄn; œÄ/2 + œÄn ) ctg x > 0, (0 + œÄn; œÄ/2 + œÄn) 9.–ù–∞–±—É–≤–∞—î –≤—ñ–¥‚Äô—î–º–Ω–∏—Ö –∑–Ω–∞—á–µ–Ω—å sin x < 0, (œÄ +2œÄn; 2œÄ +2œÄn) cos x < 0, ( œÄ/2 + 2œÄn; 3œÄ/2 + 2œÄn ) tg x < 0, ( - œÄ/2 + œÄn; 0 + œÄn) ctg x < 0, (- œÄ/2 +œÄn; 0+œÄn) 10.–ù–∞–π–±—ñ–ª—å—à–µ –∑–Ω–∞—á–µ–Ω–Ω—è sin x = 1, –ø—Ä–∏ x = œÄ/2 + 2œÄn, n ‚àà Z cos x = 1, –ø—Ä–∏ x = 2 œÄn, n ‚àà Z –ù –µ –º –∞ —î –ù –µ –º –∞ —î 11.–ù–∞–π–º–µ–Ω—à–µ –∑–Ω–∞—á–µ–Ω–Ω—è sin x = -1, –ø—Ä–∏ x = 3œÄ/2 + 2œÄn, n ‚àà Z cos x = -1, –ø—Ä–∏ x = œÄ + 2œÄn, n ‚àà Z –ù –µ –º –∞ —î –ù –µ –º –∞ —î
- 9. –Æ.–ú–∞—Ä—á—É–∫ –ö—É—Ä—Å –ª–µ–∫—Ü—ñ–π –∑ –º–∞—Ç–µ–º–∞—Ç–∏–∫–∏ –ì–ê–Ý–ú–û–ù–Ü–ß–ù–Ü –ö–û–õ–ò–í–ê–ù–ù–Ø –í–µ–ª–∏—á–∏–Ω–∏, —â–æ –∑–º—ñ–Ω—é—é—Ç—å—Å—è –∑–∞ –∑–∞–∫–æ–Ω–æ–º f(t) = A cos (œât + œÜ) ( 1 ) –∞–±–æ f(t) = A sin (œât + œÜ) ( 2 ) –≤—ñ–¥—ñ–≥—Ä–∞—é—Ç—å –≤–∞–∂–ª–∏–≤—É —Ä–æ–ª—å —É —Ñ—ñ–∑–∏—Ü—ñ. –ó–∞ —Ç–∞–∫–∏–º –∑–∞–∫–æ–Ω–æ–º –∑–º—ñ–Ω—é—î—Ç—å—Å—è, –Ω–∞–ø—Ä–∏–∫–ª–∞–¥, –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç–∞ –∫—É–ª—å–∫–∏, –ø—Ä–∏–∫—Ä—ñ–ø–ª–µ–Ω–æ—ó –¥–æ –ø—Ä—É–∂–∏–Ω–∏ (–¥–∏–≤. –º–∞–ª. 1). –ì–æ–≤–æ—Ä—è—Ç—å, —â–æ –∫—É–ª—å–∫–∞ –∑–¥—ñ–π—Å–Ω—é—î –≥–∞—Ä–º–æ–Ω—ñ—á–Ω—ñ –∫–æ–ª–∏–≤–∞–Ω–Ω—è. –§—É–Ω–∫—Ü—ñ—é (2) —Ç–∞–∫–æ–∂ –º–æ–∂–Ω–∞ –∑–∞–ø–∏—Å–∞—Ç–∏ —É –≤–∏–≥–ª—è–¥—ñ (1): A sin (œât + œÜ) = A cos (œât + œÜ - 2 œÄ ) –ü–∞—Ä–∞–º–µ—Ç—Ä–∏ –ê, œâ —ñ œÜ, —è–∫—ñ –ø–æ–≤–Ω—ñ—Å—Ç—é –≤–∏–∑–Ω–∞—á–∞—é—Ç—å –∫–æ–ª–∏–≤–∞–Ω–Ω—è (1), –º–∞—é—Ç—å —Å–ø–µ—Ü—ñ–∞–ª—å–Ω—ñ –Ω–∞–∑–≤–∏: –ê –Ω–∞–∑–∏–≤–∞—é—Ç—å –∞–º–ø–ª—ñ—Ç—É–¥–æ—é –∫–æ–ª–∏–≤–∞–Ω–Ω—è, (œâ ‚Äî —Ü–∏–∫–ª—ñ—á–Ω–æ—é (–∞–±–æ –∫—Ä—É–≥–æ–≤–æ—é) —á–∞—Å—Ç–æ—Ç–æ—é –∫–æ–ª–∏–≤–∞–Ω–Ω—è, œÜ ‚Äî –ø–æ—á–∞—Ç–∫–æ–≤–æ—é —Ñ–∞–∑–æ—é –∫–æ–ª–∏–≤–∞–Ω–Ω—è (–∑–≤–∏—á–∞–π–Ω–æ –±–µ—Ä—É—Ç—å œÜœµ[0; 2œÄ)). –ü–µ—Ä—ñ–æ–¥ —Ñ—É–Ω–∫—Ü—ñ–π A cos (œât + œÜ) —ñ A sin (œât + œÜ),—â–æ –¥–æ—Ä—ñ–≤–Ω—é—î œâ œÄ2 –Ω–∞–∑–∏–≤–∞—é—Ç—å –ø–µ—Ä—ñ–æ–¥–æ–º –≥–∞—Ä–º–æ–Ω—ñ—á–Ω–æ–≥–æ –∫–æ–ª–∏–≤–∞–Ω–Ω—è. –í–ª–∞—Å—Ç–∏–≤–æ—Å—Ç—ñ —Ñ—É–Ω–∫—Ü—ñ–π (1) —ñ (2) –∑—Ä—É—á–Ω–æ –ø—Ä–æ—ñ–ª—é—Å—Ç—Ä—É–≤–∞—Ç–∏ –Ω–∞ —Ç–∞–∫–æ–º—É –ø—Ä–∏–∫–ª–∞–¥—ñ –∑ –º–µ—Ö–∞–Ω—ñ–∫–∏. –ù–µ—Ö–∞–π —Ç–æ—á–∫–∞ –ú —Ä—É—Ö–∞—î—Ç—å—Å—è —Ä—ñ–≤–Ω–æ–º—ñ—Ä–Ω–æ –ø–æ –∫–æ–ª—É —Ä–∞–¥—ñ—É—Å–∞ R = –ê –∑ –∫—É—Ç–æ–≤–æ—é —à–≤–∏–¥–∫—ñ—Å—Ç—é œâ, —è–∫—â–æ œâ > 0, –æ–±–µ—Ä—Ç–∞–Ω–Ω—è –ø—Ä–æ—Ç–∏ –≥–æ–¥–∏–Ω–Ω–∏–∫–æ–≤–æ—ó —Å—Ç—Ä—ñ–ª–∫–∏, –∞ —è–∫—â–æ œâ < 0 ‚Äî –∑–∞ –≥–æ–¥–∏–Ω–Ω–∏–∫–æ–≤–æ—é —Å—Ç—Ä—ñ–ª–∫–æ—é), –ø—Ä–∏—á–æ–º—É –≤ –ø–æ—á–∞—Ç–∫–æ–≤–∏–π –º–æ–º–µ–Ω—Ç —á–∞—Å—É t = 0 –≤–µ–∫—Ç–æ—Ä –û–ú —É—Ç–≤–æ—Ä—é—î –∫—É—Ç œÜ –∑ –¥–æ–¥–∞—Ç–Ω–∏–º –Ω–∞–ø—Ä—è–º–æ–º –æ—Å—ñ –∞–±—Å—Ü–∏—Å (–º–∞–ª. 2). –Ý–æ–∑–≥–ª—è–Ω–µ–º–æ –¥–≤—ñ —Ñ—É–Ω–∫—Ü—ñ—ó –≤—ñ–¥ t ‚Äî –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç–∏ –ø—Ä–æ–µ–∫—Ü—ñ–π —Ç–æ—á–∫–∏ –Ω–∞ –æ—Å—ñ –∞–±—Å—Ü–∏—Å —ñ –æ—Ä–¥–∏–Ω–∞—Ç ‚Äî —Ñ—É–Ω–∫—Ü—ñ—ó x(t) —ñ y(t). –£ –º–æ–º–µ–Ω—Ç —á–∞—Å—É t –≤–µ–∫—Ç–æ—Ä –û–ú —É—Ç–≤–æ—Ä—é—î –∑ –¥–æ–¥–∞—Ç–Ω–∏–º –Ω–∞–ø—Ä—è–º–æ–º –æ—Å—ñ –û—Ö –∫—É—Ç œÜ (t), –ø—Ä–∏ —Ü—å–æ–º—É œÜ (t)= œÜ + œât –∑–∞ –∑–∞–∫–æ–Ω–æ–º —Ä—ñ–≤–Ω–æ–º—ñ—Ä–Ω–æ–≥–æ —Ä—É—Ö—É –ø–æ –∫–æ–ª—É. –ó–∞ –æ–∑–Ω–∞—á–µ–Ω–Ω—è–º —Ñ—É–Ω–∫—Ü—ñ–π —Å–∏–Ω—É—Å —ñ –∫–æ—Å–∏–Ω—É—Å x(t) = A cos œÜ(t), —Ç–æ–±—Ç–æ x(t) = –ê —Å–æs (œât + œÜ), y(t) = A sin œÜ(t), —Ç–æ–±—Ç–æ —É(t) = A sin (œât + œÜ). –í–∏–≤—á–∏–º–æ –≤–ª–∞—Å—Ç–∏–≤–æ—Å—Ç—ñ —Ü–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π, —Å–ø–∏—Ä–∞—é—á–∏—Å—å –Ω–∞ –∫—ñ–Ω–µ–º–∞—Ç–∏—á–Ω—ñ –º—ñ—Ä–∫—É–≤–∞–Ω–Ω—è. –á—Ö –ø–µ—Ä—ñ–æ–¥ –¥–æ—Ä—ñ–≤–Ω—é—î, –æ—á–µ–≤–∏–¥–Ω–æ, —á–∞—Å—É –¢, –∑–∞ —è–∫–∏–π —Ç–æ—á–∫–∞ –∑–¥—ñ–π—Å–Ω—é—î –æ–¥–∏–Ω –æ–±–µ—Ä—Ç. –î–æ–≤–∂–∏–Ω–∞ –∫–æ–ª–∞ –¥–æ—Ä—ñ–≤–Ω—é—î 2œÄ–ê, –∞ –ª—ñ–Ω—ñ–π–Ω–∞ —à–≤–∏–¥–∫—ñ—Å—Ç—å v —Ç–æ—á–∫–∏ –¥–æ—Ä—ñ–≤–Ω—é—î œâA, —Ç–æ–º—É . 22 œâ œÄ œÖ œÄ == –ê –¢ –Ý–æ–∑–≥–ª—è–Ω–µ–º–æ –æ–¥–∏–Ω –∑ –º–æ–º–µ–Ω—Ç—ñ–≤ —á–∞—Å—É to, –≤ —è–∫–∏–π —Ç–æ—á–∫–∞ –ú –∑–∞–π–º–∞—î –∫—Ä–∞–π–Ω—î –ø—Ä–∞–≤–µ –ø–æ–ª–æ–∂–µ–Ω–Ω—è. –¢–æ–¥—ñ x(to) = A, y(to) = 0. –ü–æ—á–∏–Ω–∞—é—á–∏ –∑ —Ü—å–æ–≥–æ –º–æ–º–µ–Ω—Ç—É —á–∞—Å—É, —Ñ—É–Ω–∫—Ü—ñ—è x(t) –±—É–¥–µ –Ω–∞–≤–ø–µ—Ä–µ–º—ñ–Ω–Ω–æ —Å–ø–∞–¥–∞—Ç–∏ –≤—ñ–¥ –ê –¥–æ -–ê –Ω–∞ –ø–µ—Ä—à—ñ–π –ø–æ–ª–æ–≤–∏–Ω—ñ –ø–µ—Ä—ñ–æ–¥—É —ñ –∑—Ä–æ—Å—Ç–∞—Ç–∏ –≤—ñ–¥ -–ê –¥–æ –ê –Ω–∞ –¥—Ä—É–≥—ñ–π –ø–æ–ª–æ–≤–∏–Ω—ñ –ø–µ—Ä—ñ–æ–¥—É. –ü—Ä–∏ —Ü—å–æ–º—É —Ç–æ—á–∫–∏ –º–∞–∫—Å–∏–º—É–º—É —Ñ—É–Ω–∫—Ü—ñ—ó x(t) ‚Äî —Ü–µ —Ç—ñ –º–æ–º–µ–Ω—Ç–∏ —á–∞—Å—É, –∫–æ–ª–∏ —Ç–æ—á–∫–∞ –∑–∞–π–º–∞—î –∫—Ä–∞–π–Ω—î –ø—Ä–∞–≤–µ –ø–æ–ª–æ–∂–µ–Ω–Ω—è; —Ç–æ—á–∫–∏ –º—ñ–Ω—ñ–º—É–º—É –≤—ñ–¥–ø–æ–≤—ñ–¥–∞—é—Ç—å –∫—Ä–∞–π–Ω—å–æ–º—É –ª—ñ–≤–æ–º—É –ø–æ–ª–æ–∂–µ–Ω–Ω—é, –∞ –Ω—É–ª—ñ ‚Äî –≤–µ—Ä—Ö–Ω—å–æ–º—É —ñ –Ω–∏–∂–Ω—å–æ–º—É –ø–æ–ª–æ–∂–µ–Ω–Ω—è–º. –ê–Ω–∞–ª–æ–≥—ñ—á–Ω—ñ –≤–ª–∞—Å—Ç–∏–≤–æ—Å—Ç—ñ –º–∞—î —ñ —Ñ—É–Ω–∫—Ü—ñ—è y(t); —ó—ó —Ç–æ—á–∫–∏ –º–∞–∫—Å–∏–º—É–º—É —ñ –º—ñ–Ω—ñ–º—É–º—É –≤—ñ–¥–ø–æ–≤—ñ–¥–∞—é—Ç—å –≤–µ—Ä—Ö–Ω—å–æ–º—É —ñ –Ω–∏–∂–Ω—å–æ–º—É –ø–æ–ª–æ–∂–µ–Ω–Ω—è–º —Ç–æ—á–∫–∏ –Ω–∞ –∫–æ–ª—ñ, –∞ –Ω—É–ª—ñ ‚Äî –ø—Ä–∞–≤–æ–º—É —ñ –ª—ñ–≤–æ–º—É –ø–æ–ª–æ–∂–µ–Ω–Ω—è–º. –ú–∞–ª.1 –ú–∞–ª. 2
- 10. –¢–µ–º–∞: –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó –¢–Ý–ò–ì–û–ù–û–ú–ï–¢–Ý–ò–ß–ù–Ü –§–û–Ý–ú–£–õ–ò –î–û–î–ê–í–ê–ù–ù–Ø –¢–ê –ù–ê–°–õ–Ü–î–ö–ò –ó –ù–ò–• –¢–µ–æ—Ä–µ–º–∞. –Ø–∫—ñ –± –Ω–µ –±—É–ª–∏ –∫—É—Ç–∏, –∞–±–æ —á–∏—Å–ª–∞, Œ± —ñ Œ≤, –∑–∞–≤–∂–¥–∏ cos(Œ± - Œ≤) = cos Œ± ¬∑ cos Œ≤ + sin Œ± ¬∑ sin Œ≤ –ù–∞—Å–ª—ñ–¥–∫–∏ —Ç–µ–æ—Ä–µ–º–∏ –¥–æ–¥–∞–≤–∞–Ω–Ω—è: cos(Œ± + Œ≤) = cos Œ± ¬∑ cos Œ≤ ‚Äì sin Œ± ¬∑ sin Œ≤ sin(Œ± + Œ≤) = sin Œ± ¬∑ cos Œ≤ + cos Œ± ¬∑ sin Œ≤ sin(Œ± ‚Äì Œ≤) = sin Œ± ¬∑ cos Œ≤ ‚Äì cos Œ± ¬∑ sin Œ≤ Œ≤Œ± Œ≤Œ± Œ≤Œ± tgtg1 tgtg )(tg ‚ãÖ‚àí + =+ Œ≤Œ± Œ≤Œ± Œ≤Œ± tgtg1 tgtg )(tg ‚ãÖ+ ‚àí =‚àí –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ–æ—Ä–º—É–ª–∏ –ø–æ–¥–≤—ñ–π–Ω–∏—Ö –∫—É—Ç—ñ–≤: sin 2Œ± = 2sin Œ± ¬∑ cos Œ± cos 2Œ± = cos2 Œ± ‚Äì sin2 Œ± cos 2Œ± = 1 ‚Äì 2sin2 Œ± cos 2Œ± = 2cos2 Œ± ‚Äì 1 Œ± Œ± Œ± 2 tg1 2tg 2tg ‚àí = –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ–æ—Ä–º—É–ª–∏ –ø–æ–ª–æ–≤–∏–Ω–Ω–∏—Ö –∫—É—Ç—ñ–≤: 2 cos1 2 sin Œ±Œ± ‚àí = 2 cos1 2 cos Œ±Œ± + = Œ± Œ±Œ± cos1 cos1 2 + ‚àí =tg –§–æ—Ä–º—É–ª–∏ —Å—É–º–∏ —ñ —Ä—ñ–∑–Ω–∏—Ü—ñ –æ–¥–Ω–æ–π–º–µ–Ω–Ω–∏—Ö —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π: 2 cos 2 sin2sinsin Œ≤Œ±Œ≤Œ± Œ≤Œ± ‚àí ‚ãÖ + =+ 2 cos 2 sin2sinsin Œ≤Œ±Œ≤Œ± Œ≤Œ± + ‚ãÖ ‚àí =‚àí 2 cos 2 cos2coscos Œ≤Œ±Œ≤Œ± Œ≤Œ± ‚àí ‚ãÖ + =+ 2 sin 2 sin2coscos Œ≤Œ±Œ≤Œ± Œ≤Œ± ‚àí ‚ãÖ + ‚àí=‚àí Œ≤Œ± Œ≤Œ± Œ≤Œ± coscos )sin( ‚ãÖ + =+ tgtg Œ≤Œ± Œ≤Œ± Œ≤Œ± coscos )sin( ‚ãÖ ‚àí =‚àí tgtg
- 11. –Æ.–ú–∞—Ä—á—É–∫ –ö—É—Ä—Å –ª–µ–∫—Ü—ñ–π –∑ –º–∞—Ç–µ–º–∞—Ç–∏–∫–∏ –§–æ—Ä–º—É–ª–∏ –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è –¥–æ–±—É—Ç–∫—É —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π –≤ —Å—É–º—É: 2 )cos()cos( coscos Œ≤Œ±Œ≤Œ± Œ≤Œ± ++‚àí =‚ãÖ 2 )cos()cos( sinsin Œ≤Œ±Œ≤Œ± Œ≤Œ± +‚àí‚àí =‚ãÖ 2 )sin()sin( cossin Œ≤Œ±Œ≤Œ± Œ≤Œ± ‚àí++ =‚ãÖ –û–ë–ï–Ý–ù–ï–ù–Ü –¢–Ý–ò–ì–û–ù–û–ú–ï–¢–Ý–ò–ß–ù–Ü –§–£–ù–ö–¶–Ü–á. –ù–ê–ô–ü–Ý–û–°–¢–Ü–®–Ü –¢–Ý–ò–ì–û–ù–û–ú–ï–¢–Ý–ò–ß–ù–Ü –Ý–Ü–í–ù–Ø–ù–ù–Ø –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∞ —Ñ—É–Ω–∫—Ü—ñ—è –û–±–µ—Ä–Ω–µ–Ω–∞ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∞ —Ñ—É–Ω–∫—Ü—ñ—è y = sin x y = cos x y = tg x y = ctg x y = arcsin x y = arcos x y = arctg x y = arcctg x –î–ª—è —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π —ñ –æ–±–µ—Ä–Ω–µ–Ω–∏—Ö –¥–ª—è —ó—Ö —Ñ—É–Ω–∫—Ü—ñ–π –≤–∏–∫–æ–Ω—É—é—Ç—å—Å—è —Ç–∞–∫—ñ —Ä—ñ–≤–Ω–æ—Å—Ç—ñ: sin(arcsin x) = x cos(arccos x) = x tg(arctg x) = x ctg(arcctg x) = x arcsin(sin x) = x arccos(cos x) = x arctg(tg x) = x arcctg(ctg x) = x –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏–º–∏ —Ä—ñ–≤–Ω—è–Ω–Ω—è–º–∏ –Ω–∞–∑–∏–≤–∞—é—Ç—å—Å—è —Ä—ñ–≤–Ω—è–Ω–Ω—è —É —è–∫–∏—Ö –Ω–µ–≤—ñ–¥–æ–º–∞ (–∞–±–æ –∑–º—ñ–Ω–Ω–∞) —î –∞—Ä–≥—É–º–µ–Ω—Ç–æ–º —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–æ—ó —Ñ—É–Ω–∫—Ü—ñ—ó. –¢–∞–∫—ñ —Ä—ñ–≤–Ω—è–Ω–Ω—è –∞–±–æ –Ω–µ –º–∞—é—Ç—å —Ä–æ–∑–≤'—è–∑–∫—ñ–≤, –∞–±–æ –º–∞—é—Ç—å –±–µ–∑–ª—ñ—á —Ä–æ–∑–≤'—è–∑–∫—ñ–≤ (–±–æ —Ñ—É–Ω–∫—Ü—ñ—ó –ø–µ—Ä—ñ–æ–¥–∏—á–Ω—ñ). –ó–∞–≥–∞–ª—å–Ω–æ–≥–æ —Å–ø–æ—Å–æ–±—É —Ä–æ–∑–≤'—è–∑—É–≤–∞–Ω–Ω—è —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ä—ñ–≤–Ω—è–Ω—å –Ω–µ —ñ—Å–Ω—É—î. –Ý–æ–∑–≤'—è–∑–∫–∏ –Ω–∞–π–ø—Ä–æ—Å—Ç—ñ—à–∏—Ö —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ä—ñ–≤–Ω—è–Ω—å: –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–µ —Ä—ñ–≤–Ω—è–Ω–Ω—è –Ý–æ–∑–≤'—è–∑–æ–∫ sin x = a cos x = a tg x = a x = (‚Äì1)k ¬∑arcsin a + kœÄ, k œµ Z x = ¬± arccos a + 2kœÄ, k œµ Z x = arctg a + kœÄ, k œµ Z –û–∫—Ä–µ–º—ñ –≤–∏–ø–∞–¥–∫–∏: sin x = 1, Zkkx ‚àà+= ,2 2 œÄ œÄ sin x = 0, Zkkx ‚àà= ,œÄ sin x = ‚Äì1, Zkkx ‚àà+‚àí= ,2 2 œÄ œÄ cos x = 1, Zkkx ‚àà= ,2 œÄ cos x = 0, Zkkx ‚àà+= , 2 œÄ œÄ cos x = ‚Äì1, Zkkx ‚àà+= ,2 œÄœÄ
- 12. –¢–µ–º–∞: –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó –Ý–æ–∑–≤'—è–∑–∫–∏ —Å–∫–ª–∞–¥–Ω—ñ—à–∏—Ö —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ä—ñ–≤–Ω—è–Ω—å: sin kx = a, ( ) k na x n œÄ+‚ãÖ‚àí = arcsin1 –ê–Ω–∞–ª–æ–≥—ñ—á–Ω–æ —Ä–æ–∑–≤'—è–∑—É—é—Ç—å—Å—è —Ä—ñ–≤–Ω—è–Ω–Ω—è –∑ —ñ–Ω—à–∏–º–∏ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏–º–∏ —Ñ—É–Ω–∫—Ü—ñ—è–º–∏. cos (kx + c) = a, k cna x ‚àí+¬± = œÄ2arccos –ê–Ω–∞–ª–æ–≥—ñ—á–Ω–æ —Ä–æ–∑–≤'—è–∑—É—é—Ç—å—Å—è —Ä—ñ–≤–Ω—è–Ω–Ω—è –∑ —ñ–Ω—à–∏–º–∏ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏–º–∏ —Ñ—É–Ω–∫—Ü—ñ—è–º–∏. –ù–ê–ô–ü–Ý–û–°–¢–Ü–®–Ü –¢–Ý–ò–ì–û–ù–û–ú–ï–¢–Ý–ò–ß–ù–Ü –ù–ï–Ý–Ü–í–ù–û–°–¢–Ü –Ý–æ–∑–≤'—è–∑—É–≤–∞–Ω–Ω—è —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö –Ω–µ—Ä—ñ–≤–Ω–æ—Å—Ç–µ–π –∑–≤–æ–¥–∏—Ç—å—Å—è –¥–æ —Ä–æ–∑–≤'—è–∑—É–≤–∞–Ω–Ω—è –Ω–∞–π–ø—Ä–æ—Å—Ç—ñ—à–∏—Ö —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö –Ω–µ—Ä—ñ–≤–Ω–æ—Å—Ç–µ–π –≤–∏–¥—É: sin x ‚â• a cos x ‚â• a tg x ‚â• a ctg x ‚â• a sin x > a cos x > a tg x > a ctg x > a sin x ‚⧠a cos x ‚⧠a tg x ‚⧠a ctg x ‚⧠a sin x < a cos x < a tg x < a ctg x < a –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ –Ω–µ—Ä—ñ–≤–Ω–æ—Å—Ç—ñ –∑—Ä—É—á–Ω–æ —Ä–æ–∑–≤'—è–∑—É–≤–∞—Ç–∏ –≥—Ä–∞—Ñ—ñ—á–Ω–∏–º —Å–ø–æ—Å–æ–±–æ–º.


![–¢–µ–º–∞: –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó
sin(α + 2πk) = sin α, k ϵ Z
cos(α + 2πk) = cos α, k ϵ Z
tg(α + πk) = tg α, k ϵ Z
ctg(α + πk) = ctg α, k ϵ Z
–ü—Ä–∏–∫–ª–∞–¥ –≤–∏–∑–Ω–∞—á–µ–Ω–Ω—è –ø–µ—Ä—ñ–æ–¥—É —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–æ—ó —Ñ—É–Ω–∫—Ü—ñ—ó, –∑–∞–¥–∞–Ω–æ—ó —Ñ–æ—Ä–º—É–ª–æ—é y = sin(kx + b) —ñ
y = tg(kx + b).
–î–ª—è ( )
k
Tbkxy
π2
sin =‚áí+=
( )
k
Tbkxtgy
π
=‚áí+=
–í–õ–ê–°–¢–ò–í–û–°–¢–Ü –¢–ê –ì–Ý–ê–§–Ü–ö–ò –¢–Ý–ò–ì–û–ù–û–ú–ï–¢–Ý–ò–ß–ù–ò–• –§–£–ù–ö–¶–Ü–ô
–ü—Ä–∏ –ø–æ–±—É–¥–æ–≤—ñ –≥—Ä–∞—Ñ—ñ–∫—ñ–≤ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π —Ç–∞ –ø—Ä–∏ –¥–æ—Å–ª—ñ–¥–∂–µ–Ω–Ω—ñ —Ü–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π –≤–∞–∂–ª–∏–≤—É —Ä–æ–ª—å
–≤—ñ–¥—ñ–≥—Ä–∞—î –ø–µ—Ä—ñ–æ–¥ —Ñ—É–Ω–∫—Ü—ñ–π. –ö—Ä—ñ–º —Ç–æ–≥–æ, –¥–æ –ø–æ–Ω—è—Ç—Ç—è –ø–µ—Ä—ñ–æ–¥—É –ø—Ä–∏–≤–æ–¥—è—Ç—å –ø–µ—Ä—ñ–æ–¥–∏—á–Ω—ñ –ø—Ä–æ—Ü–µ—Å–∏, —è–∫—ñ
–≤—ñ–¥–±—É–≤–∞—é—Ç—å—Å—è –≤ –∞—Å—Ç—Ä–æ–Ω–æ–º—ñ—ó, —Ç–µ—Ö–Ω—ñ—Ü—ñ, –ø—Ä–∏—Ä–æ–¥—ñ. –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó –≤–∏–∫–æ—Ä–∏—Å—Ç–æ–≤—É—é—Ç—å—Å—è –¥–æ
–º–æ–¥–µ–ª—é–≤–∞–Ω–Ω—è –∑–∞–∫–æ–Ω–æ–º—ñ—Ä–Ω–æ—Å—Ç–µ–π –∫–æ–ª–∏–≤–∞–ª—å–Ω–æ–≥–æ —Ä—É—Ö—É, –∞ —Å–∞–º–µ –º–æ–¥–µ–ª—é–≤–∞–Ω–Ω—è —Ä—ñ–≤–Ω–æ–º—ñ—Ä–Ω–æ–≥–æ –æ–±–µ—Ä—Ç–∞–ª—å–Ω–æ–≥–æ
руху. Саме з цим походженням тригонометричних функцій пов′язана одна з головних їх
особливостей – періодичність.
Вивчення тригонометричних функцій розпочнемо з побудови графіка функції, а потім «читаючи»
–≥—Ä–∞—Ñ—ñ–∫, –≤–∏–∑–Ω–∞—á–∏–º–æ —ñ –∑–∞–ø–∏—à–µ–º–æ –≤–ª–∞—Å—Ç–∏–≤–æ—Å—Ç—ñ —Ñ—É–Ω–∫—Ü—ñ—ó.
–ü–æ–±—É–¥—É–≤–∞—Ç–∏ –≥—Ä–∞—Ñ—ñ–∫ –±—É–¥—å-—è–∫–æ—ó —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–æ—ó —Ñ—É–Ω–∫—Ü—ñ—ó –º–æ–∂–Ω–∞ –¥–≤–æ–º–∞ —Å–ø–æ—Å–æ–±–∞–º–∏: –≥–µ–æ–º–µ—Ç—Ä–∏—á–Ω–∏–º —ñ
–∞–Ω–∞–ª—ñ—Ç–∏—á–Ω–∏–º.
–ì–µ–æ–º–µ—Ç—Ä–∏—á–Ω–∏–π —Å–ø–æ—Å—ñ–± –ø–æ–±—É–¥–æ–≤–∏ –æ–ø–∏—Å–∞–Ω–æ —É –ø—ñ–¥—Ä—É—á–Ω–∏–∫—É.
/ Шкіль М.І. та ін.., Алгебра і початки аналізу, 10 – 11 кл., §6 с.38 – 39 /
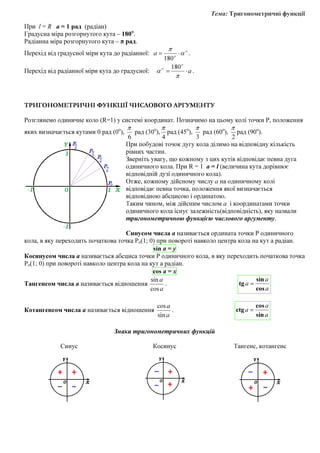
–ü–æ–±—É–¥—É—î–º–æ –≥—Ä–∞—Ñ—ñ–∫ —Ñ—É–Ω–∫—Ü—ñ—ó y = sin x –∞–Ω–∞–ª—ñ—Ç–∏—á–Ω–∏–º —Å–ø–æ—Å–æ–±–æ–º.
Оскільки найменшим додатним періодом функції є число 2π, то побудуємо графік лише на
проміжку [-π; π].
х -π -3π/4 -π/2 -π/4 0 π/4 π/2 3π/4 π
—É 0 -
2
2
-1 -
2
2
0
2
2
1
2
2
0
–ü–æ–±—É–¥–æ–≤–∞ –≥—Ä–∞—Ñ—ñ–∫–∞ —Ñ—É–Ω–∫—Ü—ñ—ó.
–ì—Ä–∞—Ñ—ñ–∫ —Ñ—É–Ω–∫—Ü—ñ—ó y = sin x –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è —Å–∏–Ω—É—Å–æ—ó–¥–æ—é.
Оскільки функція y = sin x періодична з періодом 2πп, п∈Z, то графік функції можна продовжити
–≤—ñ–¥–ø–æ–≤—ñ–¥–Ω–∏–º –ø–∞—Ä–∞–ª–µ–ª—å–Ω–∏–º –ø–µ—Ä–µ–Ω–µ—Å–µ–Ω–Ω—è–º –≥—Ä–∞—Ñ—ñ–∫–∞ y = sin x.](https://image.slidesharecdn.com/random-150218020504-conversion-gate01/85/3-4-320.jpg)
![–¢–µ–º–∞: –¢—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω—ñ —Ñ—É–Ω–∫—Ü—ñ—ó
–í–ª–∞—Å—Ç–∏–≤–æ—Å—Ç—ñ —Ç—Ä–∏–≥–æ–Ω–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö —Ñ—É–Ω–∫—Ü—ñ–π
–§—É–Ω–∫—Ü—ñ—è
–í–ª–∞—Å—Ç–∏–≤—ñ—Å—Ç—å
y = sin x y = cos x y = tg x y = ctg x
1.–û–±–ª–∞—Å—Ç—å
–≤–∏–∑–Ω–∞—á–µ–Ω–Ω—è D(y) ‚àà R D(y) ‚àà R
D(y) ‚àà R,
x ‚âÝ œÄ/2 + œÄ¬∑n
D(y) ‚àà R,
x ‚âÝ œÄ¬∑n
2.–û–±–ª–∞—Å—Ç—å
–∑–Ω–∞—á–µ–Ω—å
E(y) ‚àà [-1; 1 ] E(y) ‚àà [-1; 1 ] E(y) ‚àà R E(y) ‚àà R
3.–ü–∞—Ä–Ω—ñ—Å—Ç—å
(–Ω–µ–ø–∞—Ä–Ω—ñ—Å—Ç—å)
–ù –µ –ø –∞ —Ä –Ω –∞ –ü –∞ —Ä –Ω –∞ –ù –µ –ø –∞ —Ä –Ω –∞ –ù –µ –ø –∞ —Ä –Ω –∞
4.Періодичність T = 2πn, n ∈ Z T = 2πn, n ∈ Z T = πn, n ∈ Z T = πn, n ∈ Z
5.–ù–∞–±—É–≤–∞—î
–Ω—É–ª—å–æ–≤–∏—Ö
–∑–Ω–∞—á–µ–Ω—å
sin x = 0, –ø—Ä–∏
x = πn, n ∈ Z
cos x = 0, –ø—Ä–∏
x = π/2 + πn, n∈Z
tg x = 0, –ø—Ä–∏
x = πn, n ∈ Z
ctg x = 0, –ø—Ä–∏
x = π/2 + πn, n∈Z
6.–ü—Ä–æ–º—ñ–∂–∫–∏
–∑—Ä–æ—Å—Ç–∞–Ω–Ω—è
[ - π/2 + 2πn;
π/2 + 2πn ]
[ - π + 2πn;
0 + 2πn ]
[ - π/2 + πn;
π/2 + πn ]
–ù –µ –º –∞ —î
7.–ü—Ä–æ–º—ñ–∂–∫–∏
—Å–ø–∞–¥–∞–Ω–Ω—è
[ π/2 + 2πn;
3π/2 + 2πn ]
[ 0 + 2πn;
π + 2πn ]
–ù –µ –º –∞ —î
[ 0 + πn;
π + 2πn ]
8.–ù–∞–±—É–≤–∞—î
–¥–æ–¥–∞—Ç–Ω–∏—Ö
–∑–Ω–∞—á–µ–Ω—å
sin x > 0,
( 2πn; π + 2πn)
cos x > 0,
( - π/2 + 2πn;
π/2 + 2πn )
tg x > 0,
( 0 + πn;
π/2 + πn )
ctg x > 0,
(0 + πn; π/2 + πn)
9.–ù–∞–±—É–≤–∞—î
від’ємних
–∑–Ω–∞—á–µ–Ω—å
sin x < 0,
(π +2πn; 2π +2πn)
cos x < 0,
( π/2 + 2πn;
3π/2 + 2πn )
tg x < 0,
( - π/2 + πn;
0 + πn)
ctg x < 0,
(- π/2 +πn; 0+πn)
10.–ù–∞–π–±—ñ–ª—å—à–µ
–∑–Ω–∞—á–µ–Ω–Ω—è
sin x = 1, –ø—Ä–∏
x = π/2 + 2πn,
n ‚àà Z
cos x = 1, –ø—Ä–∏
x = 2 πn, n ∈ Z
–ù –µ –º –∞ —î –ù –µ –º –∞ —î
11.–ù–∞–π–º–µ–Ω—à–µ
–∑–Ω–∞—á–µ–Ω–Ω—è
sin x = -1, –ø—Ä–∏
x = 3π/2 + 2πn,
n ‚àà Z
cos x = -1, –ø—Ä–∏
x = π + 2πn, n ∈ Z
–ù –µ –º –∞ —î –ù –µ –º –∞ —î](https://image.slidesharecdn.com/random-150218020504-conversion-gate01/85/3-8-320.jpg)



