圏論 3分(?) クッキング
- 3. 趣旨 ● wikipedia「圏」の項を 適宜、簡略,追加して書いています – https://ja.wikipedia.org/wiki/圏_(数学) ● 圏論を …ゆるふわに説明したいなぁ 。
- 4. 目録 ● 圏の定义 ● 圏の例(群の圏) ● 関手 ● おまけ
- 5. 僕 ?名前:? ?あいや (@aiya_000) – 主兵装:?C# – 使いたいもの:?Haskell – 自学で圏論をちょくちょく進めては Twitterでご指摘をいただいている (大感謝)
- 6. 圏の定义
- 7. 圏の定义 ● 圏Cとは次のものからなる – 対象???対象X,?対象Y,?対象Z?(X,Y,Z C)∈ – 射???対象の組(X,?Y) ?に対して 射f?:?X??>?Y – 恒等射???任意の対象X ?に対して 射idX?:?X??>?X 対象X,?Y,?Z 射f?:?X??>?Y 射idX?:?X??>?X 射idY?:?Y??>?Y
- 8. 圏の定义 ● 圏Cとは次のものからなる – 合成? ● 任意の対象の組(X,Y,Z)?があり ● 射f?:?X??>?Y,?g?:?Y??>?Z?があるとき ● 射g? ?f?:?X??>?Z?○ が合成可能 射f?:?X??>?Y 射g?:?Y??>?Z ?射の合成演算子 (○) ?射 (g?○?f)?:?X??>?Z
- 9. 圏の定义 ● ちなみに – 射fの対象Xを「射のdomain(始域)」 – 射fの対象Yを「射のcodomain(終域)」という ● 射gのYは始域,?Zは終域 射f?:?X??>?Y 射g?:?Y??>?Z ?射の合成演算子 (○) ?射 (g?○?f)?:?X??>?Z
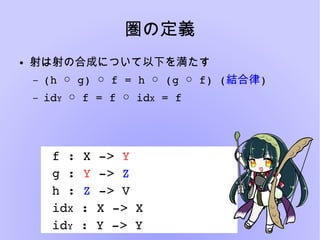
- 10. 圏の定义 ● 射は射の合成について以下を満たす – (h? ?g)? ?f?=?h? ?(g? ?f)?(○ ○ ○ ○ 結合律) – idY? ?f?=?f? ?id○ ○ X?=?f f?:?X??>?Y g?:?Y??>?Z h?:?Z??>?V idX?:?X??>?X idY?:?Y??>?Y
- 11. 圏の例(群の圏)
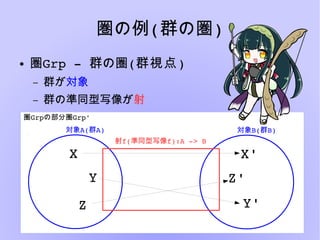
- 12. 圏の例(群の圏) ● 圏Grp???群の圏(群視点) – 群が対象 – 群の準同型写像が射 圏Grpの部分圏Grp' Z Y 対象A(群A) X X' 対象B(群B) Y' Z' 射f(準同型写像f):A??>?B
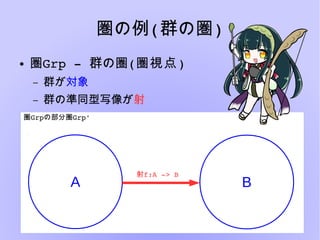
- 13. 圏の例(群の圏) ● 圏Grp???群の圏(圏視点) – 群が対象 – 群の準同型写像が射 A B 射f:A??>?B 圏Grpの部分圏Grp'
- 14. 関手
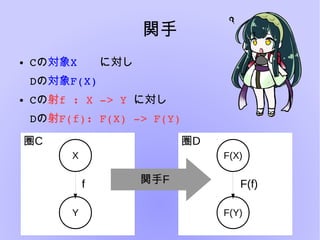
- 15. 関手 ● 2つの圏C,Dがあったとき ● 関手F:C??>?Dは圏C,Dに以下の対応関係を与える – Cの対象X に対し Dの対象F(X) – Cの射f?:?X??>?Y?に対し – Dの射F(f)?:?F(X)??>?F(Y)
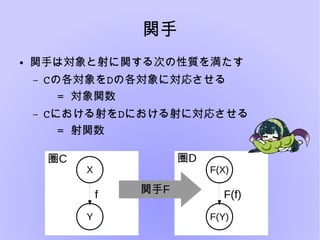
- 17. 関手 ● 関手は対象と射に関する次の性質を満たす – Cの各対象をDの各対象に対応させる =?対象関数 – Cにおける射をDにおける射に対応させる =?射関数 X Y f F(X) F(Y) F(f)関手F 圏C 圏顿
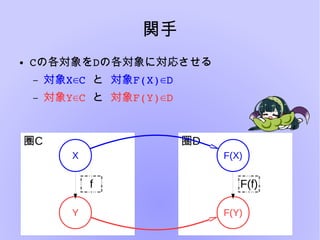
- 18. 関手 ● Cの各対象をDの各対象に対応させる – 対象X C∈ ? ?と 対象F(X) D∈ – 対象Y C∈ ? ?と 対象F(Y) D∈ X Y f F(X) F(Y) F(f) 圏C 圏顿
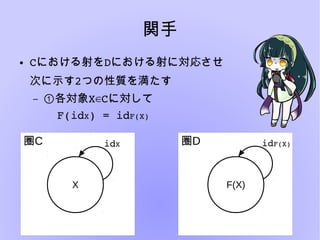
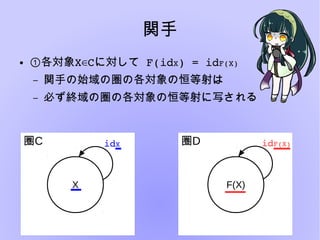
- 19. 関手 ● Cにおける射をDにおける射に対応させ 次に示す2つの性質を満たす – ①各対象X C∈ に対して F(idX)?=?idF(X) 圏C 圏顿 X idX idF(X) F(X)
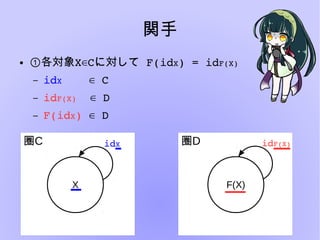
- 20. 関手 ● ①各対象X C∈ ?に対して F(idX)?=?idF(X) – idX???? ?C∈ – idF(X)?? ?D∈ – F(idX)? ?D∈ 圏C 圏顿 X idX idF(X) F(X)
- 21. 関手 ● ①各対象X C∈ ?に対して F(idX)?=?idF(X) – 関手の始域の圏の各対象の恒等射は – 必ず終域の圏の各対象の恒等射に写される 圏C 圏顿 X idX idF(X) F(X)
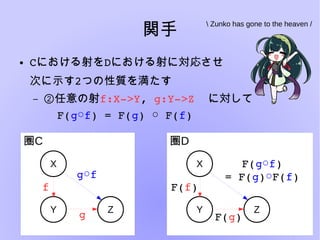
- 22. 関手 ● Cにおける射をDにおける射に対応させ 次に示す2つの性質を満たす – ②任意の射f:X?>Y,?g:Y?>Z??に対して F(g f○ )?=?F(g)? ?F(○ f) Zunko has gone to the heaven / 圏C X Y Z f g g f○ 圏顿 X Y Z F(f) F(g) F(g f○ ) =?F(g)○F(f)
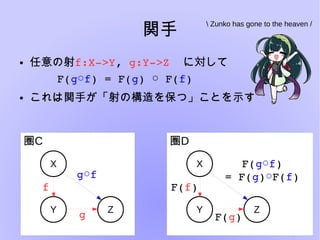
- 23. 関手 ● 任意の射f:X?>Y,?g:Y?>Z??に対して F(g f○ )?=?F(g)? ?F(○ f) ● これは関手が「射の構造を保つ」ことを示す Zunko has gone to the heaven / 圏C X Y Z f g g f○ 圏顿 X Y Z F(f) F(g) F(g f○ ) =?F(g)○F(f)
- 24. おまけ
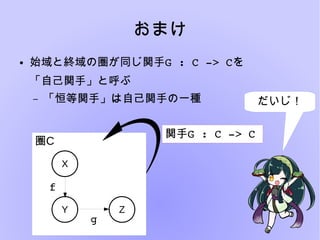
- 26. おまけ ● 始域と終域の圏が同じ関手G?:?C??>?Cを 「自己関手」と呼ぶ – 「恒等関手」は自己関手の一種 圏C X Y Z f g 関手G?:?C??>?C だいじ!
- 27. owari !