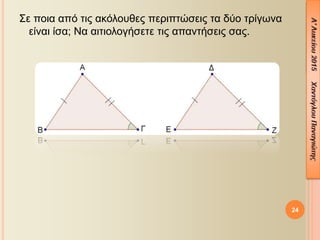
╬ô╬Á¤ë╬╝╬Á¤ä¤ü╬»╬▒: 3.1- 3.2
- 1. ╬Ü╬ò╬ª╬æ╬ø╬æ╬Ö╬ƒ 3╬ƒ: ╬ñ╬í╬è╬ô╬®╬Ø╬æ ╬ѤÇ╬Á¤ì╬©¤à╬¢╬┐¤é ╬Ü╬▒╬©╬À╬│╬À¤ä╬«¤é: ╬º╬▒╬¢¤ä¤î╬│╬╗╬┐¤à ╬á╬▒╬¢╬▒╬│╬╣¤Ä¤ä╬À¤é 1
- 2. 3.1 ╬ú╬ñ╬ƒ╬Ö╬º╬ò╬è╬æ ╬Ü╬æ╬Ö ╬ò╬è╬ö╬ù ╬ñ╬í╬Ö╬ô╬Å╬Ø╬ƒ╬Ñ 3.2 1╬ƒ ╬Ü╬í╬Ö╬ñ╬ë╬í╬Ö╬ƒ ╬Ö╬ú╬î╬ñ╬ù╬ñ╬æ╬ú ╬ñ╬í╬Ö╬ô╬Å╬Ø╬®╬Ø 2
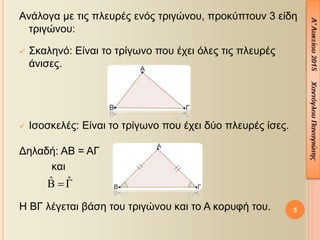
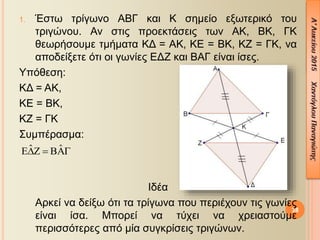
- 3. 3.1 ╬ú╬ñ╬ƒ╬Ö╬º╬ò╬è╬æ ╬Ü╬æ╬Ö ╬ò╬è╬ö╬ù ╬ñ╬í╬Ö╬ô╬Å╬Ø╬ƒ╬Ñ ╬Ü╬¼╬©╬Á ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬æ╬Æ╬ô ╬▒¤Ç╬┐¤ä╬Á╬╗╬Á╬»¤ä╬▒╬╣ ╬▒¤Ç¤î ´éó 3 ╬║╬┐¤ü¤à¤å╬¡¤é: ╬æ, ╬Æ, ╬ô ´éó 3 ¤Ç╬╗╬Á¤à¤ü╬¡¤é : ╬æ╬Æ, ╬Æ╬ô, ╬ô╬æ ´éó 3 ╬│¤ë╬¢╬»╬Á¤é: ╬ú╬À╬╝╬Á╬»¤ë¤â╬À: ´â╝ ╬Ü╬¼╬©╬Á ╬│¤ë╬¢╬»╬▒ ╬╝¤Ç╬┐¤ü╬┐¤ì╬╝╬Á ╬¢╬▒ ¤ä╬À╬¢ ¤â¤à╬╝╬▓╬┐╬╗╬»¤â╬┐¤à╬╝╬Á ╬╝╬Á ¤ä¤ü╬»╬▒ ╬│¤ü╬¼╬╝╬╝╬▒¤ä╬▒, ╬┤╬À╬╗╬▒╬┤╬«: ´â╝ ╬Ü╬¼╬©╬Á ¤Ç╬╗╬Á¤à¤ü╬¼ ╬╝¤Ç╬┐¤ü╬┐¤ì╬╝╬Á ╬¢╬▒ ¤ä╬À╬¢ ╬┐╬¢╬┐╬╝╬¼¤â╬┐¤à╬╝╬Á ╬╝╬Á ¤ä╬┐ ╬▒╬¢¤ä╬»¤â¤ä╬┐╬╣¤ç╬┐ ╬╝╬╣╬║¤ü¤î ╬│¤ü╬¼╬╝╬╝╬▒ ¤ä╬À¤é ╬▒¤Ç╬¡╬¢╬▒╬¢¤ä╬╣ ¤Ç╬╗╬Á¤à¤ü╬¼¤é, ╬┤╬À╬╗╬▒╬┤╬«: ╬æ╬Æ = ╬│, ╬Æ╬ô = ╬▒, ╬æ╬ô = ╬▓ ╦å ╦å ╦å, ,´üü ´üé ´üç ╦å ╦å ╦å ╦å ╦å ╦å, ,´üü ´Ç¢ ´üé´üü´üç ´üé ´Ç¢ ´üü´üé´üç ´üç ´Ç¢ ´üü´üç´üé 3
- 4. ´âÿ ╬á╬┐╬╣╬▒ ╬Á╬»╬¢╬▒╬╣ ¤ä╬▒ ╬║¤ì¤ü╬╣╬▒ ¤â¤ä╬┐╬╣¤ç╬Á╬»╬▒ ¤ä╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à; ╬ñ╬▒ ╬║¤ì¤ü╬╣╬▒ ¤â¤ä╬┐╬╣¤ç╬Á╬»╬▒ ╬Á╬¢¤î¤é ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à ╬Á╬»╬¢╬▒╬╣ ╬┐╬╣ ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬║╬▒╬╣ ╬┐╬╣ ╬│¤ë╬¢╬»╬Á¤é ¤ä╬┐¤à. ╬ù ¤Ç╬Á¤ü╬»╬╝╬Á¤ä¤ü╬┐¤é ¤ä╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à ╬┤╬»╬¢╬Á¤ä╬▒╬╣ ╬▒¤Ç¤î ¤ä╬┐╬¢ ¤ä¤ì¤Ç╬┐: 2¤ä = ╬▒ + ╬▓ + ╬│ ╬« 1 ( ) 2 ´ü┤ ´üí ´üó ´üº´Ç¢ ´Ç½ ´Ç½ 4
- 5. ╬æ╬¢╬¼╬╗╬┐╬│╬▒ ╬╝╬Á ¤ä╬╣¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬Á╬¢¤î¤é ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬┐¤à╬¢ 3 ╬Á╬»╬┤╬À ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à: ´â╝ ╬ú╬║╬▒╬╗╬À╬¢¤î: ╬ò╬»╬¢╬▒╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ¤Ç╬┐¤à ╬¡¤ç╬Á╬╣ ¤î╬╗╬Á¤é ¤ä╬╣¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬¼╬¢╬╣¤â╬Á¤é. ´â╝ ╬Ö¤â╬┐¤â╬║╬Á╬╗╬¡¤é: ╬ò╬»╬¢╬▒╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ¤Ç╬┐¤à ╬¡¤ç╬Á╬╣ ╬┤¤ì╬┐ ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬»¤â╬Á¤é. ╬ö╬À╬╗╬▒╬┤╬«: ╬æ╬Æ = ╬æ╬ô ╬║╬▒╬╣ ╬ù ╬Æ╬ô ╬╗╬¡╬│╬Á¤ä╬▒╬╣ ╬▓╬¼¤â╬À ¤ä╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à ╬║╬▒╬╣ ¤ä╬┐ ╬æ ╬║╬┐¤ü¤à¤å╬« ¤ä╬┐¤à. ╦å ╦å´üé ´Ç¢´üç 5
- 6. ´â╝ ╬Ö¤â¤î¤Ç╬╗╬Á¤à¤ü╬┐: ╬ò╬»╬¢╬▒╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ¤Ç╬┐¤à ╬¡¤ç╬Á╬╣ ¤î╬╗╬Á¤é ¤ä╬┐¤à ¤ä╬╣¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬»¤â╬Á¤é. ╬ö╬À╬╗╬▒╬┤╬«: ╬æ╬Æ = ╬Æ╬ô = ╬ô╬æ ╬║╬▒╬╣ ╬æ╬¢╬¼╬╗╬┐╬│╬▒ ╬╝╬Á ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ╬Á╬¢¤î¤é ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬┐¤à╬¢ 3 ╬Á╬»╬┤╬À ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à: ´â╝ ╬ƒ╬¥¤à╬│¤Ä╬¢╬╣╬┐: ╬ò╬»╬¢╬▒╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ¤Ç╬┐¤à ╬¡¤ç╬Á╬╣ 3 ╬│¤ë╬¢╬»╬Á¤é ╬┐╬¥╬Á╬»╬Á¤é. ´â╝ ╬ƒ¤ü╬©╬┐╬│¤Ä╬¢╬╣╬┐: ╬ò╬»╬¢╬▒╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ¤Ç╬┐¤à ╬¡¤ç╬Á╬╣ 1 ╬│¤ë╬¢╬»╬▒ ╬┐¤ü╬©╬« ╬║╬▒╬╣ ╬┤¤ì╬┐ ╬│¤ë╬¢╬»╬Á¤é ╬┐╬¥╬Á╬»╬Á¤é. ´â╝ ╬æ╬╝╬▓╬╗¤à╬│¤Ä╬¢╬╣╬┐: ╬ò╬»╬¢╬▒╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ¤Ç╬┐¤à ╬¡¤ç╬Á╬╣ 1 ╬│¤ë╬¢╬»╬▒ ╬▒╬╝╬▓╬╗╬Á╬»╬▒ ╬║╬▒╬╣ ╬┤¤ì╬┐ ╬│¤ë╬¢╬»╬Á¤é ╬┐╬¥╬Á╬»╬Á¤é. ╦å ╦å ╦å 60´ü» ´üü ´Ç¢ ´üé ´Ç¢ ´üç ´Ç¢ 6
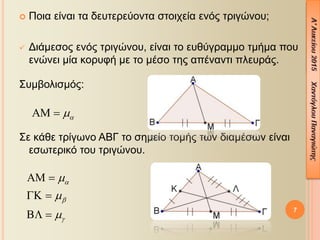
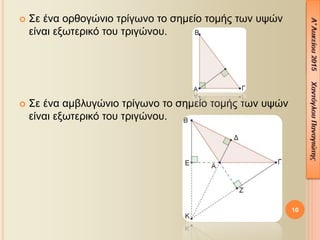
- 7. ´éó ╬á╬┐╬╣╬▒ ╬Á╬»╬¢╬▒╬╣ ¤ä╬▒ ╬┤╬Á¤à¤ä╬Á¤ü╬Á¤ì╬┐╬¢¤ä╬▒ ¤â¤ä╬┐╬╣¤ç╬Á╬»╬▒ ╬Á╬¢¤î¤é ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à; ´â╝ ╬ö╬╣╬¼╬╝╬Á¤â╬┐¤é ╬Á╬¢¤î¤é ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à, ╬Á╬»╬¢╬▒╬╣ ¤ä╬┐ ╬Á¤à╬©¤ì╬│¤ü╬▒╬╝╬╝╬┐ ¤ä╬╝╬«╬╝╬▒ ¤Ç╬┐¤à ╬Á╬¢¤Ä╬¢╬Á╬╣ ╬╝╬»╬▒ ╬║╬┐¤ü¤à¤å╬« ╬╝╬Á ¤ä╬┐ ╬╝╬¡¤â╬┐ ¤ä╬À¤é ╬▒¤Ç╬¡╬¢╬▒╬¢¤ä╬╣ ¤Ç╬╗╬Á¤à¤ü╬¼¤é. ╬ú¤à╬╝╬▓╬┐╬╗╬╣¤â╬╝¤î¤é: ╬ú╬Á ╬║╬¼╬©╬Á ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬æ╬Æ╬ô ¤ä╬┐ ¤â╬À╬╝╬Á╬»╬┐ ¤ä╬┐╬╝╬«¤é ¤ä¤ë╬¢ ╬┤╬╣╬▒╬╝╬¡¤â¤ë╬¢ ╬Á╬»╬¢╬▒╬╣ ╬Á¤â¤ë¤ä╬Á¤ü╬╣╬║¤î ¤ä╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à. 7 ´üí´ü¡´üü´üì ´Ç¢ ´üí ´üó ´üº ´ü¡ ´ü¡ ´ü¡ ´üü´üì ´Ç¢ ´üç´üï ´Ç¢ ´üé´üî ´Ç¢
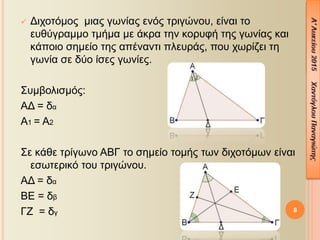
- 8. 8 ´â╝ ╬ö╬╣¤ç╬┐¤ä¤î╬╝╬┐¤é ╬╝╬╣╬▒¤é ╬│¤ë╬¢╬»╬▒¤é ╬Á╬¢¤î¤é ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à, ╬Á╬»╬¢╬▒╬╣ ¤ä╬┐ ╬Á¤à╬©¤ì╬│¤ü╬▒╬╝╬╝╬┐ ¤ä╬╝╬«╬╝╬▒ ╬╝╬Á ╬¼╬║¤ü╬▒ ¤ä╬À╬¢ ╬║╬┐¤ü¤à¤å╬« ¤ä╬À¤é ╬│¤ë╬¢╬»╬▒¤é ╬║╬▒╬╣ ╬║╬¼¤Ç╬┐╬╣╬┐ ¤â╬À╬╝╬Á╬»╬┐ ¤ä╬À¤é ╬▒¤Ç╬¡╬¢╬▒╬¢¤ä╬╣ ¤Ç╬╗╬Á¤à¤ü╬¼¤é, ¤Ç╬┐¤à ¤ç¤ë¤ü╬»╬Â╬Á╬╣ ¤ä╬À ╬│¤ë╬¢╬»╬▒ ¤â╬Á ╬┤¤ì╬┐ ╬»¤â╬Á¤é ╬│¤ë╬¢╬»╬Á¤é. ╬ú¤à╬╝╬▓╬┐╬╗╬╣¤â╬╝¤î¤é: ╬æ╬ö = ╬┤╬▒ ╬æ1 = ╬æ2 ╬ú╬Á ╬║╬¼╬©╬Á ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬æ╬Æ╬ô ¤ä╬┐ ¤â╬À╬╝╬Á╬»╬┐ ¤ä╬┐╬╝╬«¤é ¤ä¤ë╬¢ ╬┤╬╣¤ç╬┐¤ä¤î╬╝¤ë╬¢ ╬Á╬»╬¢╬▒╬╣ ╬Á¤â¤ë¤ä╬Á¤ü╬╣╬║¤î ¤ä╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à. ╬æ╬ö = ╬┤╬▒ ╬Æ╬ò = ╬┤╬▓ ╬ô╬û = ╬┤╬│
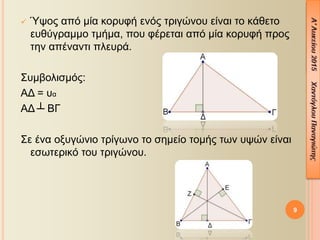
- 9. 9 ´â╝ ╬Ĥê╬┐¤é ╬▒¤Ç¤î ╬╝╬»╬▒ ╬║╬┐¤ü¤à¤å╬« ╬Á╬¢¤î¤é ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à ╬Á╬»╬¢╬▒╬╣ ¤ä╬┐ ╬║╬¼╬©╬Á¤ä╬┐ ╬Á¤à╬©¤ì╬│¤ü╬▒╬╝╬╝╬┐ ¤ä╬╝╬«╬╝╬▒, ¤Ç╬┐¤à ¤å╬¡¤ü╬Á¤ä╬▒╬╣ ╬▒¤Ç¤î ╬╝╬»╬▒ ╬║╬┐¤ü¤à¤å╬« ¤Ç¤ü╬┐¤é ¤ä╬À╬¢ ╬▒¤Ç╬¡╬¢╬▒╬¢¤ä╬╣ ¤Ç╬╗╬Á¤à¤ü╬¼. ╬ú¤à╬╝╬▓╬┐╬╗╬╣¤â╬╝¤î¤é: ╬æ╬ö = ¤à╬▒ ╬æ╬ö Ôö┤ ╬Æ╬ô ╬ú╬Á ╬¡╬¢╬▒ ╬┐╬¥¤à╬│¤Ä╬¢╬╣╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ¤ä╬┐ ¤â╬À╬╝╬Á╬»╬┐ ¤ä╬┐╬╝╬«¤é ¤ä¤ë╬¢ ¤à¤ê¤Ä╬¢ ╬Á╬»╬¢╬▒╬╣ ╬Á¤â¤ë¤ä╬Á¤ü╬╣╬║¤î ¤ä╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à.
- 10. ´éó ╬ú╬Á ╬¡╬¢╬▒ ╬┐¤ü╬©╬┐╬│¤Ä╬¢╬╣╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ¤ä╬┐ ¤â╬À╬╝╬Á╬»╬┐ ¤ä╬┐╬╝╬«¤é ¤ä¤ë╬¢ ¤à¤ê¤Ä╬¢ ╬Á╬»╬¢╬▒╬╣ ╬Á╬¥¤ë¤ä╬Á¤ü╬╣╬║¤î ¤ä╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à. ´éó ╬ú╬Á ╬¡╬¢╬▒ ╬▒╬╝╬▓╬╗¤à╬│¤Ä╬¢╬╣╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ¤ä╬┐ ¤â╬À╬╝╬Á╬»╬┐ ¤ä╬┐╬╝╬«¤é ¤ä¤ë╬¢ ¤à¤ê¤Ä╬¢ ╬Á╬»╬¢╬▒╬╣ ╬Á╬¥¤ë¤ä╬Á¤ü╬╣╬║¤î ¤ä╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à. 10
- 11. ╬ܤü╬╣¤ä╬«¤ü╬╣╬▒ ╬Ö¤â¤î¤ä╬À¤ä╬▒¤é ╬ñ¤ü╬╣╬│¤Ä╬¢¤ë╬¢ ´â╝ ╬ö¤ì╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒ ╬▒╬¢ ╬¡¤ç╬┐¤à╬¢ ¤ä╬╣¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ¤ä╬┐¤à¤é ╬║╬▒╬╣ ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ¤ä╬┐¤à¤é ╬»¤â╬Á¤é ╬╝╬»╬▒ ¤Ç¤ü╬┐¤é ╬╝╬»╬▒. ´â╝ ╬ö¤ì╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬▒¤Ç╬¡╬¢╬▒╬¢¤ä╬╣ ╬▒¤Ç¤î ╬»¤â╬Á¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬▓¤ü╬»¤â╬║╬┐╬¢¤ä╬▒╬╣ ╬»¤â╬Á¤é ╬│¤ë╬¢╬»╬Á¤é ╬║╬▒╬╣ ╬▒╬¢¤ä╬»¤â¤ä¤ü╬┐¤å╬▒. 11
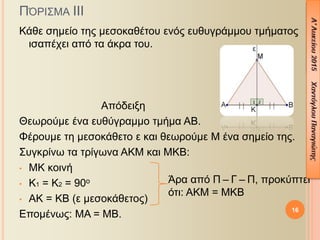
- 12. ╬ÿ╬Á¤Ä¤ü╬À╬╝╬▒ ╬Ö (1╬┐ ╬ܤü╬╣¤ä╬«¤ü╬╣╬┐: ╬á ÔÇô ╬ô ÔÇô ╬á ): ╬æ╬¢ ╬┤¤ì╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬¡¤ç╬┐¤à╬¢ ╬┤¤ì╬┐ ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬»¤â╬Á¤é ╬╝╬»╬▒ ¤Ç¤ü╬┐¤é ╬╝╬»╬▒ ╬║╬▒╬╣ ¤ä╬╣¤é ¤Ç╬Á¤ü╬╣╬Á¤ç¤î╬╝╬Á╬¢╬Á¤é ¤â╬Á ╬▒¤à¤ä╬¡¤é ╬│¤ë╬¢╬»╬Á¤é ╬»¤â╬Á¤é, ¤ä¤î¤ä╬Á ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒. 12 3.2 1╬ƒ ╬Ü╬í╬Ö╬ñ╬ë╬í╬Ö╬ƒ ╬Ö╬ú╬î╬ñ╬ù╬ñ╬æ╬ú ╬ñ╬í╬Ö╬ô╬Å╬Ø╬®╬Ø ╦å ╦å ´üä ´üä ´üü´üé ´Ç¢ ´üä´üà´â¼ ´â╝ ´â» ´â» ´üü ´Ç¢ ´üä ´âø ´üü´üé´üç ´Ç¢ ´üä´üà´üÜ´â¡ ´â¢ ´â» ´â»´üü´üç ´Ç¢ ´üä´üÜ´â« ´â¥
- 13. ╬á╬î╬í╬Ö╬ú╬£╬æ ╬Ö ╬ú╬Á ╬║╬¼╬©╬Á ╬╣¤â╬┐¤â╬║╬Á╬╗╬¡¤é ¤ä¤ü╬»╬│¤ë╬¢╬┐: ´éº ╬ƒ╬╣ ¤Ç¤ü╬┐¤â╬║╬Á╬»╬╝╬Á╬¢╬Á¤é ¤â¤ä╬À ╬▓╬¼¤â╬À ╬│¤ë╬¢╬»╬Á¤é ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬Á¤é. ´éº ╬ù ╬┤╬╣¤ç╬┐¤ä¤î╬╝╬┐¤é ¤ä╬À¤é ╬│¤ë╬¢╬»╬▒¤é ¤ä╬À¤é ╬║╬┐¤ü¤à¤å╬«¤é ╬Á╬»╬¢╬▒╬╣ ╬┤╬╣╬¼╬╝╬Á¤â╬┐¤é ╬║╬▒╬╣ ¤ì¤ê╬┐¤é. ╬ò¤Ç╬┐╬╝╬¡╬¢¤ë¤é ╬¡¤ç╬┐¤à╬╝╬Á: 13 ╦å ╦å´üé ´Ç¢ ´üç 1 2 ╦å ╦å ´ü½´üí´ü®´üü ´Ç¢ ´üü ´âø ´üé´üä ´Ç¢ ´üç´üä ´üü´üä ´ü× ´üé´üç
- 14. ╬æ╬á╬î╬ö╬ò╬Ö╬×╬ù ╬á╬ƒ╬í╬è╬ú╬£╬æ╬ñ╬ƒ╬ú 1 ´â╝ ╬ê¤â¤ä¤ë ╬æ╬Æ╬ô ╬¡╬¢╬▒ ╬╣¤â╬┐¤â╬║╬Á╬╗╬¡¤é ¤ä¤ü╬»╬│¤ë╬¢╬┐, ╬╝╬Á ╬æ╬Æ = ╬æ╬ô. ╬ª╬¡¤ü╬┐¤à╬╝╬Á ¤ä╬À ╬┤╬╣¤ç╬┐¤ä¤î╬╝╬┐ ╬æ╬ö. ╬ú¤à╬│╬║¤ü╬»╬¢╬┐¤à╬╝╬Á ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬Æ╬ö ╬║╬▒╬╣ ╬æ╬ö╬ô ÔÇó ╬æ╬ö ╬║╬┐╬╣╬¢╬« ¤Ç╬╗╬Á¤à¤ü╬¼ ÔÇó ╬æ1 = ╬æ2 (╬æ╬ö ╬┤╬╣¤ç╬┐¤ä¤î╬╝╬┐¤é) ÔÇó ╬æ╬Æ = ╬æ╬ô (¤à¤Ç¤î╬©╬Á¤â╬À) ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣ ╬æ╬Æ╬ö = ╬æ╬ö╬ô ╬║╬▒╬╣ ╬¼¤ü╬▒: ╬æ¤Ç¤î ¤ä╬À╬¢ ¤Ç╬▒¤ü╬▒¤Ç╬¼╬¢¤ë ╬╣¤â¤î¤ä╬À¤ä╬▒ ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: ╬Æ╬ö = ╬ô╬ö, ╬¼¤ü╬▒ ╬æ╬ö ╬┤╬╣╬¼╬╝╬Á¤â╬┐¤é. ╬å¤ü╬▒ ╬æ╬ö ╬Á╬»╬¢╬▒╬╣ ╬║╬▒╬╣ ¤ì¤ê╬┐¤é. 14 ╦å ╦å´üé ´Ç¢ ´üç 1 2 1 2 2 2 ╦å ╦å ╦å ╦å ╦å ╦å180 2 180 90´ü» ´ü» ´ü» ´üä ´Ç¢ ´üä ´âø ´üä ´Ç½´üä ´Ç¢ ´âø ´âù´üä ´Ç¢ ´âø ´üä ´Ç¢
- 15. ╬á╬î╬í╬Ö╬ú╬£╬æ ╬Ö╬Ö ╬ƒ╬╣ ╬│¤ë╬¢╬»╬Á¤é ╬╣¤â¤î¤Ç╬╗╬Á¤à¤ü╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬Á¤é ╬║╬▒╬╣ ╬╝╬¼╬╗╬╣¤â¤ä╬▒ 60╬┐ ╬À ╬║╬¼╬©╬Á ╬╝╬»╬▒. 15 ╦å ╦å ╦å 180 180╦å ╦å ╦å3 180 60 ╦å ╦å ╦å 3 ´ü» ´ü» ´ü» ´ü» ´â╝´üü ´Ç½ ´üé ´Ç½ ´üç ´Ç¢ ´â» ´âù´üü ´Ç¢ ´âø ´üü ´Ç¢ ´âø ´üü ´Ç¢´â¢ ´üü ´Ç¢ ´üé ´Ç¢ ´üç ´â»´â¥ ╦å ╦å ╦å 60´ü» ´üü ´Ç¢ ´üé ´Ç¢ ´üç ´Ç¢
- 16. ╬á╬î╬í╬Ö╬ú╬£╬æ ╬Ö╬Ö╬Ö ╬Ü╬¼╬©╬Á ¤â╬À╬╝╬Á╬»╬┐ ¤ä╬À¤é ╬╝╬Á¤â╬┐╬║╬▒╬©╬¡¤ä╬┐¤à ╬Á╬¢¤î¤é ╬Á¤à╬©¤à╬│¤ü╬¼╬╝╬╝╬┐¤à ¤ä╬╝╬«╬╝╬▒¤ä╬┐¤é ╬╣¤â╬▒¤Ç╬¡¤ç╬Á╬╣ ╬▒¤Ç¤î ¤ä╬▒ ╬¼╬║¤ü╬▒ ¤ä╬┐¤à. ╬æ¤Ç¤î╬┤╬Á╬╣╬¥╬À ╬ÿ╬Á¤ë¤ü╬┐¤ì╬╝╬Á ╬¡╬¢╬▒ ╬Á¤à╬©¤ì╬│¤ü╬▒╬╝╬╝╬┐ ¤ä╬╝╬«╬╝╬▒ ╬æ╬Æ. ╬ª╬¡¤ü╬┐¤à╬╝╬Á ¤ä╬À ╬╝╬Á¤â╬┐╬║╬¼╬©╬Á¤ä╬┐ ╬Á ╬║╬▒╬╣ ╬©╬Á¤ë¤ü╬┐¤ì╬╝╬Á ╬£ ╬¡╬¢╬▒ ¤â╬À╬╝╬Á╬»╬┐ ¤ä╬À¤é. ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬Ü╬£ ╬║╬▒╬╣ ╬£╬Ü╬Æ: ÔÇó ╬£╬Ü ╬║╬┐╬╣╬¢╬« ÔÇó ╬Ü1 = ╬Ü2 = 90╬┐ ÔÇó ╬æ╬Ü = ╬Ü╬Æ (╬Á ╬╝╬Á¤â╬┐╬║╬¼╬©╬Á¤ä╬┐¤é) ╬ò¤Ç╬┐╬╝╬¡╬¢¤ë¤é: ╬£╬æ = ╬£╬Æ. 16 ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: ╬æ╬Ü╬£ = ╬£╬Ü╬Æ
- 17. ╬á╬î╬í╬Ö╬ú╬£╬æ ╬ÖV ╬æ╬¢ ╬┤¤ì╬┐ ¤ä¤î╬¥╬▒ ╬Á╬¢¤î¤é ╬║¤ì╬║╬╗╬┐¤à ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒, ¤ä¤î¤ä╬Á ╬║╬▒╬╣ ╬┐╬╣ ¤ç╬┐¤ü╬┤╬¡¤é ¤ä╬┐¤à¤é ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬Á¤é. ╬ô╬¢¤ë¤ü╬»╬Â╬┐¤à╬╝╬Á ¤î¤ä╬╣: ╬æ¤Ç¤î╬┤╬Á╬╣╬¥╬À ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬ƒ╬Æ ╬║╬▒╬╣ ╬ô╬ƒ╬ö: ÔÇó ╬æ╬ƒ = ╬ƒ╬ö (¤ë¤é ╬▒╬║¤ä╬»╬¢╬Á¤é) ÔÇó ╬ƒ1 = ╬ƒ2 (╬│╬╣╬▒¤ä╬» ╬▓╬▒╬»╬¢╬┐¤à╬¢ ¤â╬Á ╬»¤â╬▒ ¤ä¤î╬¥╬▒) ÔÇó ╬Æ╬ƒ = ╬ô╬ƒ (¤ë¤é ╬▒╬║¤ä╬»╬¢╬Á¤é) ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á ╬¡¤ç╬┐¤à╬╝╬Á: ╬æ╬ƒ╬Æ = ╬ô╬ƒ╬ö ╬║╬▒╬╣ ¤â¤à╬¢╬Á¤Ç¤Ä¤é: ╬æ╬Æ = ╬ô╬ö 17 ╦å ╦å´üü´üé ´Ç¢ ´üç´üä ´âø ´üü´üÅ´üé ´Ç¢ ´üç´üÅ´üä ╬ê¤â¤ä¤ë: ╬æ╬Æ=╬ô╬ö ╬┤¤ì╬┐ ¤ä¤î╬¥╬▒
- 18. ´âÿ ╬ú╬Á ¤ä╬╣ ╬╝╬▒¤é ¤ç¤ü╬À¤â╬╣╬╝╬Á¤ì╬Á╬╣ ╬À ╬╣¤â¤î¤ä╬À¤ä╬▒ ¤ä¤ü╬╣╬│¤Ä╬¢¤ë╬¢; ╬ù ╬╣¤â¤î¤ä╬À¤ä╬▒ ¤ä¤ü╬╣╬│¤Ä╬¢¤ë╬¢ ╬©╬▒ ¤ä╬À╬¢ ¤ç¤ü╬À¤â╬╣╬╝╬┐¤Ç╬┐╬╣╬┐¤ì╬╝╬Á ╬║¤à¤ü╬»¤ë¤é ¤î¤ä╬▒╬¢: ´â╝ ╬ÿ╬¡╬╗╬┐¤à╬╝╬Á ╬¢╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬┐¤à╬╝╬Á ¤î¤ä╬╣ ╬┤¤ì╬┐ ╬Á¤à╬©¤ì╬│¤ü╬▒╬╝╬╝╬▒ ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒. ´â╝ ╬ÿ╬¡╬╗╬┐¤à╬╝╬Á ╬¢╬▒ ╬┤╬Á╬»╬¥╬┐¤à╬╝╬Á ¤î¤ä╬╣ ╬┤¤ì╬┐ ╬│¤ë╬¢╬»╬Á¤é ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬Á¤é. 18
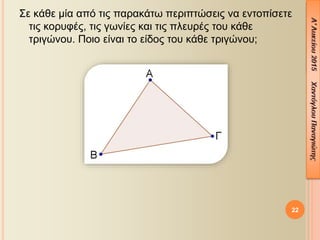
- 20. ╬ú╬Á ╬║╬¼╬©╬Á ╬╝╬»╬▒ ╬▒¤Ç¤î ¤ä╬╣¤é ¤Ç╬▒¤ü╬▒╬║╬¼¤ä¤ë ¤Ç╬Á¤ü╬╣¤Ç¤ä¤Ä¤â╬Á╬╣¤é ╬¢╬▒ ╬Á╬¢¤ä╬┐¤Ç╬»¤â╬Á¤ä╬Á ¤ä╬╣¤é ╬║╬┐¤ü¤à¤å╬¡¤é, ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ╬║╬▒╬╣ ¤ä╬╣¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ¤ä╬┐¤à ╬║╬¼╬©╬Á ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à. ╬á╬┐╬╣╬┐ ╬Á╬»╬¢╬▒╬╣ ¤ä╬┐ ╬Á╬»╬┤╬┐¤é ¤ä╬┐¤à ╬║╬¼╬©╬Á ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à; 20
- 21. ╬ú╬Á ╬║╬¼╬©╬Á ╬╝╬»╬▒ ╬▒¤Ç¤î ¤ä╬╣¤é ¤Ç╬▒¤ü╬▒╬║╬¼¤ä¤ë ¤Ç╬Á¤ü╬╣¤Ç¤ä¤Ä¤â╬Á╬╣¤é ╬¢╬▒ ╬Á╬¢¤ä╬┐¤Ç╬»¤â╬Á¤ä╬Á ¤ä╬╣¤é ╬║╬┐¤ü¤à¤å╬¡¤é, ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ╬║╬▒╬╣ ¤ä╬╣¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ¤ä╬┐¤à ╬║╬¼╬©╬Á ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à. ╬á╬┐╬╣╬┐ ╬Á╬»╬¢╬▒╬╣ ¤ä╬┐ ╬Á╬»╬┤╬┐¤é ¤ä╬┐¤à ╬║╬¼╬©╬Á ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à; 21
- 22. ╬ú╬Á ╬║╬¼╬©╬Á ╬╝╬»╬▒ ╬▒¤Ç¤î ¤ä╬╣¤é ¤Ç╬▒¤ü╬▒╬║╬¼¤ä¤ë ¤Ç╬Á¤ü╬╣¤Ç¤ä¤Ä¤â╬Á╬╣¤é ╬¢╬▒ ╬Á╬¢¤ä╬┐¤Ç╬»¤â╬Á¤ä╬Á ¤ä╬╣¤é ╬║╬┐¤ü¤à¤å╬¡¤é, ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ╬║╬▒╬╣ ¤ä╬╣¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ¤ä╬┐¤à ╬║╬¼╬©╬Á ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à. ╬á╬┐╬╣╬┐ ╬Á╬»╬¢╬▒╬╣ ¤ä╬┐ ╬Á╬»╬┤╬┐¤é ¤ä╬┐¤à ╬║╬¼╬©╬Á ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à; 22
- 23. ╬ú╬Á ¤Ç╬┐╬╣╬▒ ╬▒¤Ç¤î ¤ä╬╣¤é ╬▒╬║¤î╬╗╬┐¤à╬©╬Á¤é ¤Ç╬Á¤ü╬╣¤Ç¤ä¤Ä¤â╬Á╬╣¤é ¤ä╬▒ ╬┤¤ì╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒; ╬Ø╬▒ ╬▒╬╣¤ä╬╣╬┐╬╗╬┐╬│╬«¤â╬Á¤ä╬Á ¤ä╬╣¤é ╬▒¤Ç╬▒╬¢¤ä╬«¤â╬Á╬╣¤é ¤â╬▒¤é. 23
- 24. ╬ú╬Á ¤Ç╬┐╬╣╬▒ ╬▒¤Ç¤î ¤ä╬╣¤é ╬▒╬║¤î╬╗╬┐¤à╬©╬Á¤é ¤Ç╬Á¤ü╬╣¤Ç¤ä¤Ä¤â╬Á╬╣¤é ¤ä╬▒ ╬┤¤ì╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒; ╬Ø╬▒ ╬▒╬╣¤ä╬╣╬┐╬╗╬┐╬│╬«¤â╬Á¤ä╬Á ¤ä╬╣¤é ╬▒¤Ç╬▒╬¢¤ä╬«¤â╬Á╬╣¤é ¤â╬▒¤é. 24
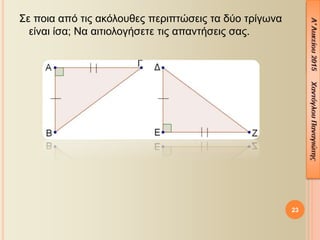
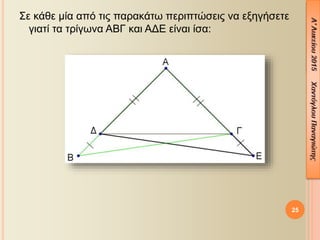
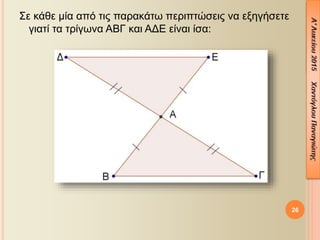
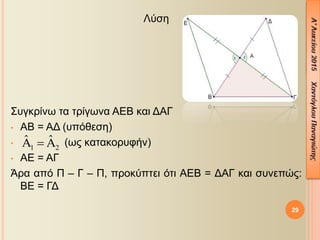
- 25. ╬ú╬Á ╬║╬¼╬©╬Á ╬╝╬»╬▒ ╬▒¤Ç¤î ¤ä╬╣¤é ¤Ç╬▒¤ü╬▒╬║╬¼¤ä¤ë ¤Ç╬Á¤ü╬╣¤Ç¤ä¤Ä¤â╬Á╬╣¤é ╬¢╬▒ ╬Á╬¥╬À╬│╬«¤â╬Á¤ä╬Á ╬│╬╣╬▒¤ä╬» ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬Æ╬ô ╬║╬▒╬╣ ╬æ╬ö╬ò ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒: 25
- 26. ╬ú╬Á ╬║╬¼╬©╬Á ╬╝╬»╬▒ ╬▒¤Ç¤î ¤ä╬╣¤é ¤Ç╬▒¤ü╬▒╬║╬¼¤ä¤ë ¤Ç╬Á¤ü╬╣¤Ç¤ä¤Ä¤â╬Á╬╣¤é ╬¢╬▒ ╬Á╬¥╬À╬│╬«¤â╬Á¤ä╬Á ╬│╬╣╬▒¤ä╬» ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬Æ╬ô ╬║╬▒╬╣ ╬æ╬ö╬ò ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒: 26
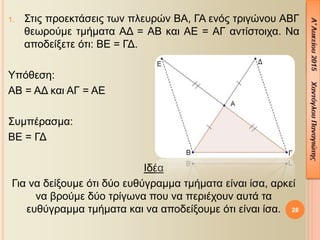
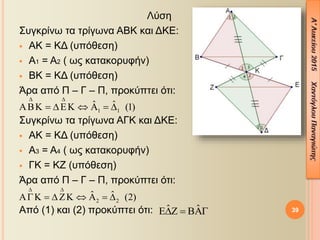
- 28. 1. ╬ú¤ä╬╣¤é ¤Ç¤ü╬┐╬Á╬║¤ä╬¼¤â╬Á╬╣¤é ¤ä¤ë╬¢ ¤Ç╬╗╬Á¤à¤ü¤Ä╬¢ ╬Æ╬æ, ╬ô╬æ ╬Á╬¢¤î¤é ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à ╬æ╬Æ╬ô ╬©╬Á¤ë¤ü╬┐¤ì╬╝╬Á ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬æ╬ö = ╬æ╬Æ ╬║╬▒╬╣ ╬æ╬ò = ╬æ╬ô ╬▒╬¢¤ä╬»¤â¤ä╬┐╬╣¤ç╬▒. ╬Ø╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬Á¤ä╬Á ¤î¤ä╬╣: ╬Æ╬ò = ╬ô╬ö. ╬ѤǤî╬©╬Á¤â╬À: ╬æ╬Æ = ╬æ╬ö ╬║╬▒╬╣ ╬æ╬ô = ╬æ╬ò ╬ú¤à╬╝¤Ç╬¡¤ü╬▒¤â╬╝╬▒: ╬Æ╬ò = ╬ô╬ö ╬Ö╬┤╬¡╬▒ ╬ô╬╣╬▒ ╬¢╬▒ ╬┤╬Á╬»╬¥╬┐¤à╬╝╬Á ¤î¤ä╬╣ ╬┤¤ì╬┐ ╬Á¤à╬©¤ì╬│¤ü╬▒╬╝╬╝╬▒ ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒, ╬▒¤ü╬║╬Á╬» ╬¢╬▒ ╬▓¤ü╬┐¤ì╬╝╬Á ╬┤¤ì╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ¤Ç╬┐¤à ╬¢╬▒ ¤Ç╬Á¤ü╬╣╬¡¤ç╬┐¤à╬¢ ╬▒¤à¤ä╬¼ ¤ä╬▒ ╬Á¤à╬©¤ì╬│¤ü╬▒╬╝╬╝╬▒ ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬║╬▒╬╣ ╬¢╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬┐¤à╬╝╬Á ¤î¤ä╬╣ ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒. 28
- 29. ╬ø¤ì¤â╬À ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬ò╬Æ ╬║╬▒╬╣ ╬ö╬æ╬ô ÔÇó ╬æ╬Æ = ╬æ╬ö (¤à¤Ç¤î╬©╬Á¤â╬À) ÔÇó (¤ë¤é ╬║╬▒¤ä╬▒╬║╬┐¤ü¤à¤å╬«╬¢) ÔÇó ╬æ╬ò = ╬æ╬ô ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣ ╬æ╬ò╬Æ = ╬ö╬æ╬ô ╬║╬▒╬╣ ¤â¤à╬¢╬Á¤Ç¤Ä¤é: ╬Æ╬ò = ╬ô╬ö 29 1 2 ╦å ╦å´üü ´Ç¢ ´üü
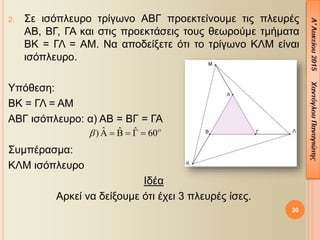
- 30. 2. ╬ú╬Á ╬╣¤â¤î¤Ç╬╗╬Á¤à¤ü╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬æ╬Æ╬ô ¤Ç¤ü╬┐╬Á╬║¤ä╬Á╬»╬¢╬┐¤à╬╝╬Á ¤ä╬╣¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬æ╬Æ, ╬Æ╬ô, ╬ô╬æ ╬║╬▒╬╣ ¤â¤ä╬╣¤é ¤Ç¤ü╬┐╬Á╬║¤ä╬¼¤â╬Á╬╣¤é ¤ä╬┐¤à¤é ╬©╬Á¤ë¤ü╬┐¤ì╬╝╬Á ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬Æ╬Ü = ╬ô╬ø = ╬æ╬£. ╬Ø╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬Á¤ä╬Á ¤î¤ä╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬Ü╬ø╬£ ╬Á╬»╬¢╬▒╬╣ ╬╣¤â¤î¤Ç╬╗╬Á¤à¤ü╬┐. ╬ѤǤî╬©╬Á¤â╬À: ╬Æ╬Ü = ╬ô╬ø = ╬æ╬£ ╬æ╬Æ╬ô ╬╣¤â¤î¤Ç╬╗╬Á¤à¤ü╬┐: ╬▒) ╬æ╬Æ = ╬Æ╬ô = ╬ô╬æ ╬ú¤à╬╝¤Ç╬¡¤ü╬▒¤â╬╝╬▒: ╬Ü╬ø╬£ ╬╣¤â¤î¤Ç╬╗╬Á¤à¤ü╬┐ ╬Ö╬┤╬¡╬▒ ╬æ¤ü╬║╬Á╬» ╬¢╬▒ ╬┤╬Á╬»╬¥╬┐¤à╬╝╬Á ¤î¤ä╬╣ ╬¡¤ç╬Á╬╣ 3 ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬»¤â╬Á¤é. 30 ╦å ╦å ╦å) 60´ü» ´üó ´üü ´Ç¢ ´üé ´Ç¢ ´üç ´Ç¢
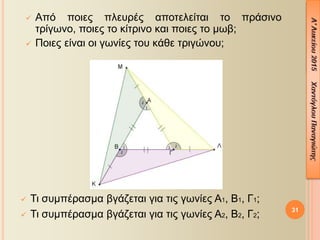
- 31. 31 ´â╝ ╬æ¤Ç¤î ¤Ç╬┐╬╣╬Á¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬▒¤Ç╬┐¤ä╬Á╬╗╬Á╬»¤ä╬▒╬╣ ¤ä╬┐ ¤Ç¤ü╬¼¤â╬╣╬¢╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐, ¤Ç╬┐╬╣╬Á¤é ¤ä╬┐ ╬║╬»¤ä¤ü╬╣╬¢╬┐ ╬║╬▒╬╣ ¤Ç╬┐╬╣╬Á¤é ¤ä╬┐ ╬╝¤ë╬▓; ´â╝ ╬á╬┐╬╣╬Á¤é ╬Á╬»╬¢╬▒╬╣ ╬┐╬╣ ╬│¤ë╬¢╬»╬Á¤é ¤ä╬┐¤à ╬║╬¼╬©╬Á ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à; ´â╝ ╬ñ╬╣ ¤â¤à╬╝¤Ç╬¡¤ü╬▒¤â╬╝╬▒ ╬▓╬│╬¼╬Â╬Á¤ä╬▒╬╣ ╬│╬╣╬▒ ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ╬æ1, ╬Æ1, ╬ô1; ´â╝ ╬ñ╬╣ ¤â¤à╬╝¤Ç╬¡¤ü╬▒¤â╬╝╬▒ ╬▓╬│╬¼╬Â╬Á¤ä╬▒╬╣ ╬│╬╣╬▒ ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ╬æ2, ╬Æ2, ╬ô2;
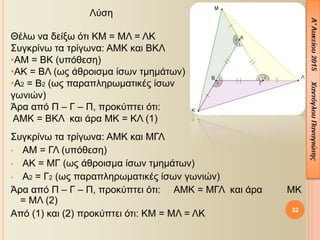
- 32. ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒: ╬æ╬£╬Ü ╬║╬▒╬╣ ╬£╬ô╬ø ÔÇó ╬æ╬£ = ╬ô╬ø (¤à¤Ç¤î╬©╬Á¤â╬À) ÔÇó ╬æ╬Ü = ╬£╬ô (¤ë¤é ╬¼╬©¤ü╬┐╬╣¤â╬╝╬▒ ╬»¤â¤ë╬¢ ¤ä╬╝╬À╬╝╬¼¤ä¤ë╬¢) ÔÇó ╬æ2 = ╬ô2 (¤ë¤é ¤Ç╬▒¤ü╬▒¤Ç╬╗╬À¤ü¤ë╬╝╬▒¤ä╬╣╬║╬¡¤é ╬»¤â¤ë╬¢ ╬│¤ë╬¢╬╣¤Ä╬¢) ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: ╬æ╬£╬Ü = ╬£╬ô╬ø ╬║╬▒╬╣ ╬¼¤ü╬▒ ╬£╬Ü = ╬£╬ø (2) ╬æ¤Ç¤î (1) ╬║╬▒╬╣ (2) ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: ╬Ü╬£ = ╬£╬ø = ╬ø╬Ü 32 ╬ø¤ì¤â╬À ╬ÿ╬¡╬╗¤ë ╬¢╬▒ ╬┤╬Á╬»╬¥¤ë ¤î¤ä╬╣ ╬Ü╬£ = ╬£╬ø = ╬ø╬Ü ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒: ╬æ╬£╬Ü ╬║╬▒╬╣ ╬Æ╬Ü╬ø ÔÇó╬æ╬£ = ╬Æ╬Ü (¤à¤Ç¤î╬©╬Á¤â╬À) ÔÇó╬æ╬Ü = ╬Æ╬ø (¤ë¤é ╬¼╬©¤ü╬┐╬╣¤â╬╝╬▒ ╬»¤â¤ë╬¢ ¤ä╬╝╬À╬╝╬¼¤ä¤ë╬¢) ÔÇó╬æ2 = ╬Æ2 (¤ë¤é ¤Ç╬▒¤ü╬▒¤Ç╬╗╬À¤ü¤ë╬╝╬▒¤ä╬╣╬║╬¡¤é ╬»¤â¤ë╬¢ ╬│¤ë╬¢╬╣¤Ä╬¢) ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: ╬æ╬£╬Ü = ╬Æ╬Ü╬ø ╬║╬▒╬╣ ╬¼¤ü╬▒ ╬£╬Ü = ╬Ü╬ø (1)
- 33. 33 3. ╬Ø╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬Á¤ä╬Á ¤î¤ä╬╣ ¤â¤ä╬╣¤é ╬┐╬╝¤î╬╗╬┐╬│╬Á¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬┤¤ì╬┐ ╬»¤â¤ë╬¢ ¤ä¤ü╬╣╬│¤Ä╬¢¤ë╬¢ ╬▒╬¢¤ä╬╣¤â¤ä╬┐╬╣¤ç╬┐¤ì╬¢ ╬»¤â╬Á¤é ╬┤╬╣╬¼╬╝╬Á¤â╬┐╬╣. ╬ѤǤî╬©╬Á¤â╬À: ╬æ╬Æ╬ô = ╬ö╬ò╬û ╬æ╬£, ╬ö╬Ü ╬┤╬╣╬¼╬╝╬Á¤â╬┐╬╣ ╬Æ╬£ = ╬£╬ô ╬║╬▒╬╣ ╬Ü╬ò = ╬Ü╬û ╬ú¤à╬╝¤Ç╬¡¤ü╬▒¤â╬╝╬▒: ╬æ╬£ = ╬ö╬Ü ╬Ö╬┤╬¡╬▒ ╬æ¤ü╬║╬Á╬» ╬¢╬▒ ╬┤╬Á╬»╬¥¤ë ¤î¤ä╬╣ ╬┤¤ì╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬▒, ¤Ç╬┐¤à ¤Ç╬Á¤ü╬╣╬¡¤ç╬┐¤à╬¢ ¤ä╬╣¤é ╬┤╬╣╬▒╬╝╬¡¤â╬┐¤à¤é, ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒.
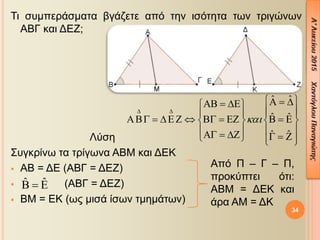
- 34. ╬ñ╬╣ ¤â¤à╬╝¤Ç╬Á¤ü╬¼¤â╬╝╬▒¤ä╬▒ ╬▓╬│╬¼╬Â╬Á¤ä╬Á ╬▒¤Ç¤î ¤ä╬À╬¢ ╬╣¤â¤î¤ä╬À¤ä╬▒ ¤ä¤ë╬¢ ¤ä¤ü╬╣╬│¤Ä╬¢¤ë╬¢ ╬æ╬Æ╬ô ╬║╬▒╬╣ ╬ö╬ò╬û; ╬ø¤ì¤â╬À ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬Æ╬£ ╬║╬▒╬╣ ╬ö╬ò╬Ü ´éº ╬æ╬Æ = ╬ö╬ò (╬æ╬Æ╬ô = ╬ö╬ò╬û) ´éº (╬æ╬Æ╬ô = ╬ö╬ò╬û) ´éº ╬Æ╬£ = ╬ò╬Ü (¤ë¤é ╬╝╬╣¤â╬¼ ╬»¤â¤ë╬¢ ¤ä╬╝╬À╬╝╬¼¤ä¤ë╬¢) 34 ╦å ╦å ╦å ╦å ╦å ╦å ´ü½´üí´ü® ´üä ´üä ´â¼ ´â╝´üü ´Ç¢ ´üä´üü´üé ´Ç¢ ´üä´üà´â¼ ´â╝ ´â» ´â»´â» ´â» ´â» ´â» ´üü´üé´üç ´Ç¢ ´üä´üà ´üÜ ´âø ´üé´üç ´Ç¢ ´üà´üÜ ´üé ´Ç¢ ´üà´â¡ ´â¢ ´â¡ ´â¢ ´â» ´â» ´â» ´â»´üü´üç ´Ç¢ ´üä´üÜ ´üç ´Ç¢ ´üÜ´â« ´â¥ ´â» ´â»´â« ´â¥ ╦å ╦å´üé ´Ç¢ ´üà ╬æ¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: ╬æ╬Æ╬£ = ╬ö╬ò╬Ü ╬║╬▒╬╣ ╬¼¤ü╬▒ ╬æ╬£ = ╬ö╬Ü
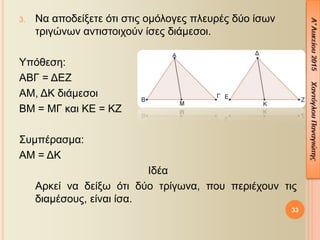
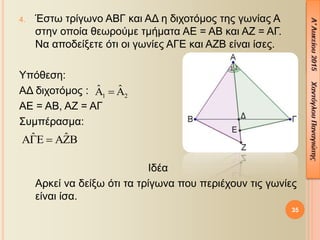
- 35. 35 4. ╬ê¤â¤ä¤ë ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬æ╬Æ╬ô ╬║╬▒╬╣ ╬æ╬ö ╬À ╬┤╬╣¤ç╬┐¤ä¤î╬╝╬┐¤é ¤ä╬À¤é ╬│¤ë╬¢╬»╬▒¤é ╬æ ¤â¤ä╬À╬¢ ╬┐¤Ç╬┐╬»╬▒ ╬©╬Á¤ë¤ü╬┐¤ì╬╝╬Á ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬æ╬ò = ╬æ╬Æ ╬║╬▒╬╣ ╬æ╬û = ╬æ╬ô. ╬Ø╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬Á¤ä╬Á ¤î¤ä╬╣ ╬┐╬╣ ╬│¤ë╬¢╬»╬Á¤é ╬æ╬ô╬ò ╬║╬▒╬╣ ╬æ╬û╬Æ ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬Á¤é. ╬ѤǤî╬©╬Á¤â╬À: ╬æ╬ö ╬┤╬╣¤ç╬┐¤ä¤î╬╝╬┐¤é : ╬æ╬ò = ╬æ╬Æ, ╬æ╬û = ╬æ╬ô ╬ú¤à╬╝¤Ç╬¡¤ü╬▒¤â╬╝╬▒: ╬Ö╬┤╬¡╬▒ ╬æ¤ü╬║╬Á╬» ╬¢╬▒ ╬┤╬Á╬»╬¥¤ë ¤î¤ä╬╣ ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ¤Ç╬┐¤à ¤Ç╬Á¤ü╬╣╬¡¤ç╬┐¤à╬¢ ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒. 1 2 ╦å ╦å´üü ´Ç¢ ´üü ╦å ╦å´üü´üç´üà ´Ç¢ ´üü´üÜ´üé
- 36. ╬ø¤ì¤â╬À ╬ú¤à╬│╬║¤ü╬»╬¢╬┐¤à╬╝╬Á ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬Æ╬û ╬║╬▒╬╣ ╬æ╬ô╬ò: ´éº ╬æ╬Æ = ╬æ╬ò (¤à¤Ç¤î╬©╬Á¤â╬À) ´éº (╬æ╬ö ╬┤╬╣¤ç╬┐¤ä¤î╬╝╬┐¤é) ´éº ╬æ╬ô = ╬æ╬û (¤à¤Ç¤î╬©╬Á¤â╬À) 36 1 2 ╦å ╦å´üü ´Ç¢ ´üü ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣ ╬æ╬Æ╬û = ╬æ╬ô╬ò ╬║╬▒╬╣ ¤â¤à╬¢╬Á¤Ç¤Ä¤é: ╦å ╦å´üü´üç´üà ´Ç¢ ´üü´üÜ´üé
- 38. 38 1. ╬ê¤â¤ä¤ë ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬æ╬Æ╬ô ╬║╬▒╬╣ ╬Ü ¤â╬À╬╝╬Á╬»╬┐ ╬Á╬¥¤ë¤ä╬Á¤ü╬╣╬║¤î ¤ä╬┐¤à ¤ä¤ü╬╣╬│¤Ä╬¢╬┐¤à. ╬æ╬¢ ¤â¤ä╬╣¤é ¤Ç¤ü╬┐╬Á╬║¤ä╬¼¤â╬Á╬╣¤é ¤ä¤ë╬¢ ╬æ╬Ü, ╬Æ╬Ü, ╬ô╬Ü ╬©╬Á¤ë¤ü╬«¤â╬┐¤à╬╝╬Á ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬Ü╬ö = ╬æ╬Ü, ╬Ü╬ò = ╬Æ╬Ü, ╬Ü╬û = ╬ô╬Ü, ╬¢╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬Á¤ä╬Á ¤î¤ä╬╣ ╬┐╬╣ ╬│¤ë╬¢╬»╬Á¤é ╬ò╬ö╬û ╬║╬▒╬╣ ╬Æ╬æ╬ô ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬Á¤é. ╬ѤǤî╬©╬Á¤â╬À: ╬Ü╬ö = ╬æ╬Ü, ╬Ü╬ò = ╬Æ╬Ü, ╬Ü╬û = ╬ô╬Ü ╬ú¤à╬╝¤Ç╬¡¤ü╬▒¤â╬╝╬▒: ╬Ö╬┤╬¡╬▒ ╬æ¤ü╬║╬Á╬» ╬¢╬▒ ╬┤╬Á╬»╬¥¤ë ¤î¤ä╬╣ ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ¤Ç╬┐¤à ¤Ç╬Á¤ü╬╣╬¡¤ç╬┐¤à╬¢ ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒. ╬£¤Ç╬┐¤ü╬Á╬» ╬¢╬▒ ¤ä¤ì¤ç╬Á╬╣ ╬¢╬▒ ¤ç¤ü╬Á╬╣╬▒¤â¤ä╬┐¤ì╬╝╬Á ¤Ç╬Á¤ü╬╣¤â¤â¤î¤ä╬Á¤ü╬Á¤é ╬▒¤Ç¤î ╬╝╬»╬▒ ¤â¤à╬│╬║¤ü╬»¤â╬Á╬╣¤é ¤ä¤ü╬╣╬│¤Ä╬¢¤ë╬¢. ╦å ╦å´üà´üä´üÜ ´Ç¢ ´üé´üü´üç
- 39. ╬ø¤ì¤â╬À ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬Æ╬Ü ╬║╬▒╬╣ ╬ö╬Ü╬ò: ´éº ╬æ╬Ü = ╬Ü╬ö (¤à¤Ç¤î╬©╬Á¤â╬À) ´éº ╬æ1 = ╬æ2 ( ¤ë¤é ╬║╬▒¤ä╬▒╬║╬┐¤ü¤à¤å╬«╬¢) ´éº ╬Æ╬Ü = ╬Ü╬ö (¤à¤Ç¤î╬©╬Á¤â╬À) ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬æ╬ô╬Ü ╬║╬▒╬╣ ╬ö╬Ü╬ò: ´éº ╬æ╬Ü = ╬Ü╬ö (¤à¤Ç¤î╬©╬Á¤â╬À) ´éº ╬æ3 = ╬æ4 ( ¤ë¤é ╬║╬▒¤ä╬▒╬║╬┐¤ü¤à¤å╬«╬¢) ´éº ╬ô╬Ü = ╬Ü╬û (¤à¤Ç¤î╬©╬Á¤â╬À) ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: ╬æ¤Ç¤î (1) ╬║╬▒╬╣ (2) ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: 39 1 1 ╦å ╦å (1) ´üä ´üä ´üü´üé´üï ´Ç¢ ´üä´üà´üï ´âø ´üü ´Ç¢ ´üä 2 2 ╦å ╦å (2) ´üä ´üä ´üü´üç´üï ´Ç¢ ´üä ´üÜ´üï ´âø ´üü ´Ç¢ ´üä ╦å ╦å´üà´üä´üÜ ´Ç¢ ´üé´üü´üç
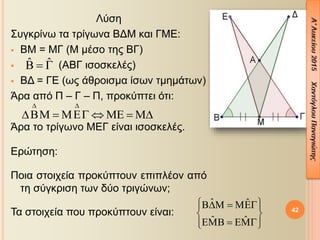
- 40. 40 2. ╬ö╬»╬¢╬Á¤ä╬▒╬╣ ╬╣¤â╬┐¤â╬║╬Á╬╗╬¡¤é ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬æ╬Æ╬ô. ╬ú¤ä╬╣¤é ¤Ç¤ü╬┐╬Á╬║¤ä╬¼¤â╬Á╬╣¤é ¤ä¤ë╬¢ ╬»¤â¤ë╬¢ ¤Ç╬╗╬Á¤à¤ü¤Ä╬¢ ¤ä╬┐¤à ╬Æ╬æ, ╬ô╬æ ╬©╬Á¤ë¤ü╬┐¤ì╬╝╬Á ╬»¤â╬▒ ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬æ╬ö, ╬æ╬ò ╬▒╬¢¤ä╬»¤â¤ä╬┐╬╣¤ç╬▒. ╬æ╬¢ ╬£ ¤ä╬┐ ╬╝╬¡¤â╬┐ ¤ä╬À¤é ╬▓╬¼¤â╬À¤é ╬Æ╬ô, ╬¢╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬Á¤ä╬Á ¤î¤ä╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬£╬ö╬ò ╬Á╬»╬¢╬▒╬╣ ╬╣¤â╬┐¤â╬║╬Á╬╗╬¡¤é. ╬á╬í╬ƒ╬ú╬ƒ╬º╬ù ╬î¤ä╬▒╬¢ ╬╝╬▒¤é ╬╗╬¡╬Á╬╣ ¤î¤ä╬╣ ¤Ç¤ü╬┐╬Á╬║¤ä╬Á╬»╬¢╬┐¤à╬╝╬Á ¤ä╬╣¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é ╬Æ╬æ ╬║╬▒╬╣ ╬ô╬æ ╬Á╬¢╬¢╬┐╬Á╬» ¤î¤ä╬╣ ╬À ¤Ç¤ü╬┐╬¡╬║¤ä╬▒¤â╬À ╬│╬»╬¢╬Á¤ä╬▒╬╣ ╬▒¤Ç¤î ¤ä╬À ╬╝╬Á¤ü╬╣╬¼ ¤ä╬┐¤à ¤â╬À╬╝╬Á╬»╬┐¤à ¤Ç╬┐¤à ╬Á╬╝¤å╬▒╬¢╬»╬Â╬Á¤ä╬▒╬╣ ╬┤╬Á¤ì¤ä╬Á¤ü╬┐ ¤â¤ä╬À╬¢ ╬┐╬¢╬┐╬╝╬▒¤â╬»╬▒ ¤ä╬┐¤à ╬Á¤à╬©¤à╬│¤ü╬¼╬╝╬╝╬┐¤à ¤ä╬╝╬«╬╝╬▒¤ä╬┐¤é. ╬ö╬À╬╗╬▒╬┤╬« ¤â¤ä╬À ¤â¤à╬│╬║╬Á╬║¤ü╬╣╬╝╬¡╬¢╬À ╬¼¤â╬║╬À¤â╬À ╬▒¤Ç¤î ¤ä╬À ╬╝╬Á¤ü╬╣╬¼ ¤ä╬┐¤à ¤â╬À╬╝╬Á╬»╬┐¤à ╬æ.
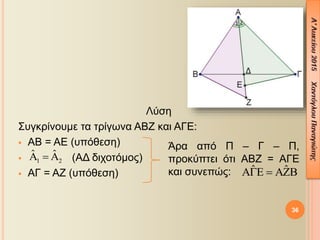
- 41. 41 2. ╬ö╬»╬¢╬Á¤ä╬▒╬╣ ╬╣¤â╬┐¤â╬║╬Á╬╗╬¡¤é ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬æ╬Æ╬ô. ╬ú¤ä╬╣¤é ¤Ç¤ü╬┐╬Á╬║¤ä╬¼¤â╬Á╬╣¤é ¤ä¤ë╬¢ ╬»¤â¤ë╬¢ ¤Ç╬╗╬Á¤à¤ü¤Ä╬¢ ¤ä╬┐¤à ╬Æ╬æ, ╬ô╬æ ╬©╬Á¤ë¤ü╬┐¤ì╬╝╬Á ╬»¤â╬▒ ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬æ╬ö, ╬æ╬ò ╬▒╬¢¤ä╬»¤â¤ä╬┐╬╣¤ç╬▒. ╬æ╬¢ ╬£ ¤ä╬┐ ╬╝╬¡¤â╬┐ ¤ä╬À¤é ╬▓╬¼¤â╬À¤é ╬Æ╬ô, ╬¢╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬Á¤ä╬Á ¤î¤ä╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬£╬ö╬ò ╬Á╬»╬¢╬▒╬╣ ╬╣¤â╬┐¤â╬║╬Á╬╗╬¡¤é. ╬ѤǤî╬©╬Á¤â╬À: ╬æ╬ö = ╬æ╬ò ╬£ ╬╝╬¡¤â╬┐ ╬Æ╬ô Ôçö ╬Æ╬£ = ╬£╬ô ╬ú¤à╬╝¤Ç╬¡¤ü╬▒¤â╬╝╬▒: ╬£╬ö╬ò ╬╣¤â╬┐¤â╬║╬Á╬╗╬¡¤é ╬Ö╬┤╬¡╬▒ ╬æ¤ü╬║╬Á╬» ╬¢╬▒ ╬┤╬Á╬»╬¥¤ë ¤î¤ä╬╣ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬¡¤ç╬Á╬╣ ╬┤¤ì╬┐ ╬»¤â╬Á¤é ¤Ç╬╗╬Á¤à¤ü╬¡¤é
- 42. ╬ø¤ì¤â╬À ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬Æ╬ö╬£ ╬║╬▒╬╣ ╬ô╬£╬ò: ´éº ╬Æ╬£ = ╬£╬ô (╬£ ╬╝╬¡¤â╬┐ ¤ä╬À¤é ╬Æ╬ô) ´éº (╬æ╬Æ╬ô ╬╣¤â╬┐¤â╬║╬Á╬╗╬¡¤é) ´éº ╬Æ╬ö = ╬ô╬ò (¤ë¤é ╬¼╬©¤ü╬┐╬╣¤â╬╝╬▒ ╬»¤â¤ë╬¢ ¤ä╬╝╬À╬╝╬¼¤ä¤ë╬¢) ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: ╬å¤ü╬▒ ¤ä╬┐ ¤ä¤ü╬»╬│¤ë╬¢╬┐ ╬£╬ò╬ô ╬Á╬»╬¢╬▒╬╣ ╬╣¤â╬┐¤â╬║╬Á╬╗╬¡¤é. ╬ò¤ü¤Ä¤ä╬À¤â╬À: ╬á╬┐╬╣╬▒ ¤â¤ä╬┐╬╣¤ç╬Á╬»╬▒ ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬┐¤à╬¢ ╬Á¤Ç╬╣¤Ç╬╗╬¡╬┐╬¢ ╬▒¤Ç¤î ¤ä╬À ¤â¤ì╬│╬║¤ü╬╣¤â╬À ¤ä¤ë╬¢ ╬┤¤ì╬┐ ¤ä¤ü╬╣╬│¤Ä╬¢¤ë╬¢; ╬ñ╬▒ ¤â¤ä╬┐╬╣¤ç╬Á╬»╬▒ ¤Ç╬┐¤à ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬┐¤à╬¢ ╬Á╬»╬¢╬▒╬╣: 42 ╦å ╦å´üé ´Ç¢ ´üç ´üä ´üä ´üä´üé´üì ´Ç¢ ´üì´üà´üç ´âø ´üì´üà ´Ç¢ ´üì´üä ╦å ╦å ╦å ╦å ´â¼ ´â╝´üé´üä´üì ´Ç¢ ´üì´üà´üç´â» ´â» ´â¡ ´â¢ ´üà´üì´üé ´Ç¢ ´üà´üì´üç´â» ´â»´â« ´â¥
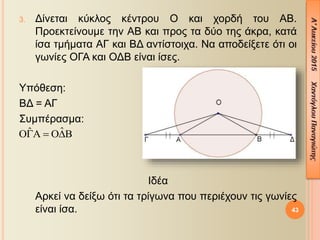
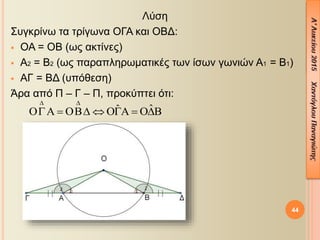
- 43. 43 3. ╬ö╬»╬¢╬Á¤ä╬▒╬╣ ╬║¤ì╬║╬╗╬┐¤é ╬║╬¡╬¢¤ä¤ü╬┐¤à ╬ƒ ╬║╬▒╬╣ ¤ç╬┐¤ü╬┤╬« ¤ä╬┐¤à ╬æ╬Æ. ╬á¤ü╬┐╬Á╬║¤ä╬Á╬»╬¢╬┐¤à╬╝╬Á ¤ä╬À╬¢ ╬æ╬Æ ╬║╬▒╬╣ ¤Ç¤ü╬┐¤é ¤ä╬▒ ╬┤¤ì╬┐ ¤ä╬À¤é ╬¼╬║¤ü╬▒, ╬║╬▒¤ä╬¼ ╬»¤â╬▒ ¤ä╬╝╬«╬╝╬▒¤ä╬▒ ╬æ╬ô ╬║╬▒╬╣ ╬Æ╬ö ╬▒╬¢¤ä╬»¤â¤ä╬┐╬╣¤ç╬▒. ╬Ø╬▒ ╬▒¤Ç╬┐╬┤╬Á╬»╬¥╬Á¤ä╬Á ¤î¤ä╬╣ ╬┐╬╣ ╬│¤ë╬¢╬»╬Á¤é ╬ƒ╬ô╬æ ╬║╬▒╬╣ ╬ƒ╬ö╬Æ ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬Á¤é. ╬ѤǤî╬©╬Á¤â╬À: ╬Æ╬ö = ╬æ╬ô ╬ú¤à╬╝¤Ç╬¡¤ü╬▒¤â╬╝╬▒: ╬Ö╬┤╬¡╬▒ ╬æ¤ü╬║╬Á╬» ╬¢╬▒ ╬┤╬Á╬»╬¥¤ë ¤î¤ä╬╣ ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ¤Ç╬┐¤à ¤Ç╬Á¤ü╬╣╬¡¤ç╬┐¤à╬¢ ¤ä╬╣¤é ╬│¤ë╬¢╬»╬Á¤é ╬Á╬»╬¢╬▒╬╣ ╬»¤â╬▒. ╦å╦å´üÅ´üç´üü ´Ç¢ ´üÅ´üä´üé
- 44. ╬ø¤ì¤â╬À ╬ú¤à╬│╬║¤ü╬»╬¢¤ë ¤ä╬▒ ¤ä¤ü╬»╬│¤ë╬¢╬▒ ╬ƒ╬ô╬æ ╬║╬▒╬╣ ╬ƒ╬Æ╬ö: ´éº ╬ƒ╬æ = ╬ƒ╬Æ (¤ë¤é ╬▒╬║¤ä╬»╬¢╬Á¤é) ´éº ╬æ2 = ╬Æ2 (¤ë¤é ¤Ç╬▒¤ü╬▒¤Ç╬╗╬À¤ü¤ë╬╝╬▒¤ä╬╣╬║╬¡¤é ¤ä¤ë╬¢ ╬»¤â¤ë╬¢ ╬│¤ë╬¢╬╣¤Ä╬¢ ╬æ1 = ╬Æ1) ´éº ╬æ╬ô = ╬Æ╬ö (¤à¤Ç¤î╬©╬Á¤â╬À) ╬å¤ü╬▒ ╬▒¤Ç¤î ╬á ÔÇô ╬ô ÔÇô ╬á, ¤Ç¤ü╬┐╬║¤ì¤Ç¤ä╬Á╬╣ ¤î¤ä╬╣: 44 ╦å╦å ´üä ´üä ´üÅ´üç´üü ´Ç¢ ´üÅ´üé´üä ´âø ´üÅ´üç´üü ´Ç¢ ´üÅ´üä´üé
- 45. ╬ñ╬¡╬╗╬┐¤é ╬á╬▒¤ü╬┐¤à¤â╬»╬▒¤â╬À¤é!!! ╬ò¤Ç╬╣╬╝╬¡╬╗╬Á╬╣╬▒: ╬º╬▒╬¢¤ä¤î╬│╬╗╬┐¤à ╬á╬▒╬¢╬▒╬│╬╣¤Ä¤ä╬À¤é ╬ñ╬À╬╗╬¡¤å¤ë╬¢╬┐ ╬ò¤Ç╬╣╬║╬┐╬╣╬¢Ë¼╬¢╬»╬▒¤é: