确率モデルを用いた3顿点群レジストレーション
?
0 likes?2,271 views
2019年の関東CV勉強会で発表した資料です。 Coherent Point Drift, GMMReg, FilterRegなど確率モデルを用いた点群レジストレーションについてのまとめです。
确率モデルを用いた3顿点群レジストレーション
- 2. 自己紹介 ● 名前：neka-nat ● 職業：製造メーカのソフトウェアエンジニア ● 普段のお仕事 ○ ロボットや画像処理のソフト開発 ● 最近の興味：3D点群処理、CG ● CV勉強会初参加です、よろしくお願いします！
- 3. 本日の内容 1. 3D点群レジストレーションについて 2. 点群レジストレーションの种类 3. 確率モデルベースの点群レジストレーション 4. まとめ
- 4. 3D点群レジストレーションとは ● 解きたい問題 ○ 点同士の対応関係が取れていない2つの点集合 ○ 一方の点群(モデル)を変形させてもう一方の点群(シーン)に合わせる ○ その際の変形のパラメタを求める問題 Transformation ● 回転?並進 ● アフィン変形 ● 非剛体変形 モデル点群 シーン点群
- 5. 3D点群レジストレーションとは ● 用途 ○ 物体の位置姿勢推定 ○ SLAM ○ 3次元点群の再構成 ● 今回のまとめの範囲 ○ 使用するデータは点群のみ ○ 確率モデルを使った手法 物体の位置姿勢を推定して把 持する 移動しながら地図を作る
- 8. ICP(Iterative Closest Point)(1/3) ● 点群のレジストレーションで最も基本となる手法 ● 比較的近い初期値から精度良く位置合わせを行う手法 ● アルゴリズム 1. モデル点群とシーン点群の対応を最近傍探索NYによって求める 2. 変形パラメタR, tを対応点同士の二乗誤差の最小化によって求める 3. 1, 2を交互に収束するまで繰り返し計算する モデル点群X シーン点群Y 最近傍点 回転R, 並進t x0 x1 x2 x3 x4 x5 y5 y4 y3 y2 y1 y0 x0 x1 x2 x3 x4 x5 y5 y4 y3 y2 y1 y0
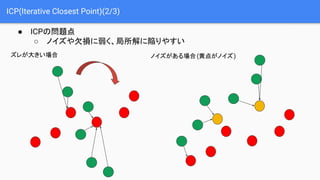
- 9. ICP(Iterative Closest Point)(2/3) ● ICPの問題点 ○ ノイズや欠損に弱く、局所解に陥りやすい ズレが大きい場合 ノイズがある場合(黄点がノイズ)
- 10. ICP(Iterative Closest Point)(3/3) ● ICPの改善方法 ○ 外れ値の除去 ○ 誤差の重み付け ○ ICPベースのアルゴリズム ■ TrICP, EM-ICP, LM-ICP, IRLS-ICP, Sparse-ICP ● ICP以外の方法 ○ すべての点を組み合わせた誤差を考える ○ RPM(Robust Point Matching), KC(Kernel Correlation)
- 11. 点群レジストレーションの分類 ● グローバルに解を求める手法 ○ 初期値がなくても解を求められる ○ 特徴量を求めたり、計算量は比較的多め ○ 主なアルゴリズム ■ Go-ICP(2013), Super4pcs(2014), Fast Global Registration(2016) ● 非剛体に対応した手法 ○ Thin-Plate-Splineなどを使用して非剛体の変形に対応 ○ 主なアルゴリズム ■ TPS-RPM(2003), MR-RPM(2017) ● 機械学習を用いた手法 ○ データから点群の特徴量や位置合わせの移動方向そのものを学習させる ○ 主なアルゴリズム ■ Discriminative Optimization(2017), 3DFeatNet(2018)
- 12. 确率モデルを用いた手法
- 13. 确率モデルを用いた手法の特徴 ● 局所最適な手法(初期値が必要)、ICPよりロバスト ● 定式化の段階で変形は抽象的に扱われており非剛体にも拡張されているものが多 い ● 確率分布の計算に時間がかかるのが課題であったが、近年、高速化された手法が 提案されており、精度?速度ともにICPに勝ってきている
- 14. CPD(Coherent Point Drift)(1/5) ● 2010年, IEEE TPAMI ● 点群のレジストレーションを確率モデルの尤度最大化として定式化 ● モデル点群Xからシーン点群Yが確率的に生成されるモデルを考える モデル点群 シーン点群
- 15. CPD(Coherent Point Drift)(2/5) ● 変形後のモデルの点をx(θ)で記述し、p(yi|xj)をガウス分布とする ● この確率モデルの尤度最大化をEMアルゴリズムで解く ● 変形はスケール付き剛体変換、アフィン変換、NonRigid変換に対応 最尤推定(EMアルゴリズム)により変形パラメタθを求める M+1番目の要素として一様分布を足す
- 16. CPD(Coherent Point Drift)(3/5) ● 最終的に以下のコスト(負の対数尤度期待値)をEMアルゴリズムで解く ● 変形パラメタθだけでなくガウス分布の分散σ2も同時に推定する ● Estep ○ 現状のパラメタθを用いてP(xj(θ)|yi)を求める ● Mstep ○ 各変形関数に応じてQの微分を0にするパラメタθを求める Estepで計算 各点の距離計算
- 17. CPD(Coherent Point Drift)(3/5) ● Mstepはスケール付き剛体変換、アフィン変換、NonRigid変換に合わせて式展 開される スケール付き剛体変換 GRBFを用いたNon-rigidモデル
- 18. CPD(Coherent Point Drift)(4/5) ● CPDの問題点：計算がすごく遅い ○ 計算が遅いのはEstepのガウス変換とMstepの行列計算 ○ Estep, Mstep共にO(MN)の計算量 ● Estepのガウス変換にFGT(fast gauss transform)を用いることでO(M+N)になり、 少し改善される ● ICPよりロバストに解が求まる ICP CPD
- 19. GMMReg(1/2) ● 2011年, IEEE TPAMI ● モデルおよびシーン点群両方に対して確率分布から生成された点群であると仮定 する ● それぞれの確率分布同士のL2距離をニュートン法によって最小化する x 1 x 2 x 3 x M ... y 1 y 2 y 3 y N ... GMM1 GMM2 L2 distance モデル点群 シーン点群 Φx1, …, Φxm μx1, ..., μxm σx1, …, σxm Φy1, …, Φyn μy1, ..., μyn σy1, …, σyn
- 20. GMMReg(2/2) ● 非剛体レジストレーションに対してはTPS(Thin Plate Spline)を使用 ○ 制御点をコントロールすることで空間を変形させる ● CPDよりも精度?速度は優位だが、初期値依存性が高まった
- 21. SVR(Support Vector Registration) ● ICCV2015 ● GMMRegをベースにGMMの構築にOneClassSVMを使用した ● OneClassSVMで得られたSV?重みをガウス分布のパラメタに変換する ● GMMRegよりオクルージョンなどに対してロバストに点群の表現が可能 GMM SVGM
- 22. NDT-D2D ● ICRA2012 ● NDT(Normal Distributions Transform)とは ○ 点群を一定の大きさのセルで分割し、各セル内で平均と分散を計算する ● GMMRegと同様に2つの点群のNDTを求め、それらをGMMとみなしてL2距離最小 化問題を解く ● この手法以前にPoint-to-NDTを用いたものがあったが、それに比べて精度?速度と もに向上している
- 23. ECMPR(Expectation Conditional Maximization for Point Registration) ● 2011年 IEEE, TPAMI ● 剛体と剛体の関節機構に対してレジストレーションを行う手法の提案 ● EMアルゴリズムの一種であるExpectation conditional maximization (ECM)や異 方性共分散を用いている ● デモでは手の動きや人の動きに対してレジストレーションを行っている
- 24. JRMPC(Joint Registration of Multiple Point Cloud) ● 2017年, IEEE TPAMI ● 複数の点群を同時にレジストレーション行うための手法 ● 定式化はCPDのやり方に近い ORB-SLAM2 RGBD-SLAM Elasticfusion
- 25. GMMTree(1/2) ● ECCV2018のNvidia Researchの論文 ● 階層化したGMMを用いることで細かく見る部分と荒く見る部分を分けて表現できるよ うにした ● これにより精度を担保しながら速度向上を達成した ● 階層固定する場合と適応的に変化させる場合でテスト ○ 適応的な方が精度?速度的に良さそう
- 27. FilterReg(1/5) ● CVPR2019のOral, MITのロボットの研究室 ● CPDで用いた確率モデルの逆モデルを用いることで高速に解けるように定式化 CPD FilterReg
- 28. FilterReg(2/5) ● MstepでのΣ計算がモデル点群に対してのみになっている ○ CPDではΣ計算がモデル点群とシーン点群の2重であった ● さらにEstepでPermutohedral Lattice Filter(2010)を使用することで高速化 ● 分散の固定/更新、point-to-point/point-to-planeを選択できる Permutohedral Lattice Filterを用いて高速化
- 29. FilterReg(3/5) ● ICP?CPDとの比較としてStanford Bunnyにノイズを加えてテスト ○ 滨颁笔よりロバスト、颁笔顿よりも100倍以上速い
- 30. FilterReg(4/5) ● Stanford Lounge 诲补迟补蝉别迟を用いて他の手法との比较
- 31. FilterReg(5/5) ● 非剛体への拡張として関節を持つ物体に応用 ○ ロボットなどの剛体ベースのリンク機構 ○ DQB(Dual quaternion blending)を用いた柔軟表皮モデル ● Dynamic Fusionと組み合わせて、より精度良く人の動きに追従するデモを示している
- 32. まとめ ● 確率モデルベースの点群レジストレーションアルゴリズムを紹介した ● 精度?計算速度?ロバスト性において確率モデルベースの手法は優位 ● 非剛体にも対応できる ● 時間があれば最初に分類したレジストレーション各種法についても調べてみたいで す
- 33. 論文リンク, OSSなど ● CPD ○ https://arxiv.org/pdf/0905.2635.pdf ○ https://github.com/gadomski/cpd ○ https://github.com/siavashk/pycpd ● GMMReg ○ https://www.researchgate.net/publication/224207506_Robust_Point_Set _Registration_Using_Gaussian_Mixture_Models ○ https://github.com/bing-jian/gmmreg ● SVR ○ https://www.cv-foundation.org/openaccess/content_iccv_2015/papers/C ampbell_An_Adaptive_Data_ICCV_2015_paper.pdf ○ https://sites.google.com/view/djcampbell/research-software ● NDT-D2D ○ http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.817.5962&rep =rep1&type=pdf ○ http://wiki.ros.org/ndt_registration
- 34. 論文リンク, OSSなど ● ECMPR ○ https://hal.inria.fr/inria-00590265/document ○ https://team.inria.fr/perception/research/ecmpr/ ● JRMPC ○ https://arxiv.org/pdf/1609.01466.pdf ○ https://team.inria.fr/perception/research/jrmpc/ ● GMMTree ○ https://research.nvidia.com/publication/2018-09_HGMM-Registration ● FilterReg ○ https://arxiv.org/abs/1811.10136 ○ https://sites.google.com/view/?lterreg/home ○ https://bitbucket.org/gaowei19951004/poser/src/master/ ○ https://github.com/neka-nat/probreg
- 35. おわり