3.pdf
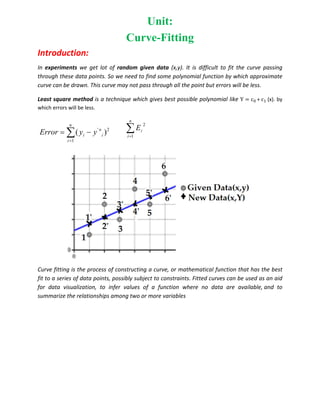
- 1. Unit: Curve-Fitting Introduction: In experiments we get lot of random given data (x,y). It is difficult to fit the curve passing through these data points. So we need to find some polynomial function by which approximate curve can be drawn. This curve may not pass through all the point but errors will be less. Least square method is a technique which gives best possible polynomial like Y c + c (x). by which errors will be less. ' 2 1 ( ) n n i i i Error y y ο½ ο½ ο ο₯ ο₯ ο½ n i i E 1 2 Curve fitting is the process of constructing a curve, or mathematical function that has the best fit to a series of data points, possibly subject to constraints. Fitted curves can be used as an aid for data visualization, to infer values of a function where no data are available, and to summarize the relationships among two or more variables
- 2. A first degree polynomial equation: Yn c + c (x). A first degree polynomial equation is an exact fit through any two points with distinct x coordinates. A second degree polynomial: Yn c + c (x) + c (x)2 . Fitting a Line (first degree polynomial) equation: n= number of data points β β β β . β OR Determinants: d=det d1= d2= Constants: c0=d1/d & c1=d2/d Fitting a Line : + (x). Problem: Using least square method Fit a line: Yn c + c (x) X 1 2 3 4 Y 2 6 12 20 Solution: n= number of data points=4 β β β β . β X Y 1 2 1 2 2 3 4 12 3 12 9 36 4 20 16 80 β =10 β . 40 β 30 β 130
- 3. OR Determinants: d=det 1 1 2 =20 d1= Dd2= =120 Constants: C0=d1/d = β 5 and C1=d2/d=6 Best fitted line: + (X). ANSWER: + (X). Line Flowchart
- 4. % LINE FITTING Yf=C0+C1(X) clc clear all %-------------Direct input of Data----------- x=[1 2 3 4]; y=[2 6 12 20]; n=length(x) %--------------OR-User UInput of data----- % n=input('Enter n='); % for i=1:n % fprintf('Enter x(%d)=',i); % x(i)=input(''); % fprintf('Enter y(%d)=',i); % y(i)=input(''); % end %-------------------------------------------- s1=sum(x); s2=sum(x.^2); s3=sum(y); s4=sum(x.*y); %-------------------------------------------- d=[n s1; s1 s2]; d1=[s3 s1; s4 s2]; d2=[n s3; s1 s4]; d=det(d); d1=det(d1); d2=det(d2); %-------------------------------------------- c0=d1/d; c1=d2/d; fprintf('BEST FIT ,Yn=%0.3f+%0.3f(X)n',c0,c1) %-------------------------------------------- yn=c0+c1*x; plot(x,y,'*',x,yn) %--------------------------------------------
- 5. Solved Problems Fit the line yn=c0+c1*x x=[1 2 3 4]; y=[2 6 12 20]; βββββββββββββββββ X Y X2 XY βββββββββββββββββ 1 2 1 2 2 6 4 12 3 12 9 36 4 20 16 80 βββββββββββββββββ 10 40 30 130 Calculate d d1 d2 c 0 c1 by you BEST FIT ,Yn=β5.000+6.000(X) Fit the line yn=c0+c1*x L=a0+a1T x=[ 20 30 40 50 60 70]; y=[800.3 800.4 800.6 800.7 800.9 801]; βββββββββββββββββββββββ X Y X2 X.*Y βββββββββββββββββββββββ 20 800 400 16006 30 800 900 24012 40 801 1600 32024 50 801 2500 40035 60 801 3600 48054 70 801 4900 56070 βββββββββββββββββββββββββββββ 270 4804 13900 216201 βββββββββββββββββββββββββββββ Calculate d d1 d2 c 0 c1 by you
- 6. BEST FIT ,Yn=799.994+0.015(X) Fitting a second degree polynomial: + (X) + (X)2 β β β β β β β β 0 1 2 β β β . 1 2 1 2 3 2 3 4 0 1 2 5 6 7 D det 1 2 1 2 3 2 3 4 D1 det 5 1 2 6 2 3 7 3 4 D2 Det 5 2 1 6 3 2 7 4 D3 Det 1 5 1 2 6 2 3 7 Constants: C0=d1/d , C1=d2/d and C2=d3/d Problem: Using least square method fit a second degree polynomial + (X) + (X)2 X 1 2 3 4 5 6 7 8 9 Y 2 6 7 8 10 11 11 10 9 Solution: β β β β β β β β β β β = 0 1 2
- 7. Table calculatins to be done by you X Y X2 X3 X4 XY XY2 S1 S5 S2 S3 S4 S6 S7 . 45 74 286 2025 15333 421 2771 On making table and solving S1 45, S2 286, S3 2025, S4 15333, s5 74 , s6 421, s7 2771, D det 166320 D1 det β154440 D2 Det D3 Det β44460 Constants: C0=D1/D = β0.9286 C1=D2/D= 3. C2=D3/D= β0.2673 Best fitted parabola: . .+3.523(X) 0.267(X)2
- 8. Program % Quadratic FITTING Yf=C0+C1(X)+C2(x^2); % Quadratic FITTING Yf=C0+C1(X)+C2(x^2); clc clear all %ββββββββββββββββββββββββββββββββββββββββββββββββββββββ x=[1 2 3 4 5 6 7 8 9]; y=[2 6 7 8 10 11 11 10 9]; n=9; %ββββββββββββββββββββββββββββββββββββββββββββββββββββββ x2=x.^2; x3=x.^3; x4=x.^4; xy=x.*y; x2y=(x.^2).*y; s1=sum(x); s2=sum(x2); s3=sum(x3); s4=sum(x4); s5=sum(y); s6=sum(xy); s7=sum(x2y); %ββββββββββββββββββββββββββββββββββββββββββββββββββββββ d=[n s1 s2; s1 s2 s3 s2 s3 s4]; d1=[s5 s1 s2; s6 s2 s3 s7 s3 s4]; d2=[n s5 s2; s1 s6 s3 s2 s7 s4]; d3=[n s1 s5; s1 s2 s6 s2 s3 s7]; %ββββββββββββββββββββββββββββββββββββββββββββββββββββββ d=det(d); d1=det(d1); d2=det(d2); d3=det(d3); c0=d1/d; c1=d2/d; c2=d3/d; %ββββββββββββββββββββββββββββββββββββββββββββββββββββββ fprintf('BEST FIT ,Yn=%0.3f+%0.3f(X)+%0.3f(x^2)n',c0,c1,c2) %ββββββββββββββββββββββββββββββββββββββββββββββββββββββ yn=c0+c1*x+c2*x2; plot(x,y,'*',x,yn,'r') %ββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββ Option for i=1:n fprintf('%0.0f %0.0f %0.0f %0.0f %0.0f %0.0f %0.0f n',x(i),y(i),x2(i),x3(i),x4(i),xy(i),x2y(i)) end fprintf('ββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββ n'); fprintf('%0.0f %0.0f %0.0f %0.0f %0.0f %0.0f %0.0f n',s1, s5,s2,s3,s4,s6,s7)
- 9. Solved Problem Fit the following quadratic/2nd degree/ parabolic curve + (X) + (X)2 x=[β4 β3 β2 β1 0 1 2 3 4 5]; y=[21 12 4 1 2 7 15 30 45 67]; βββββββββββββββββββββββββββββββββββββββ X Y x2 x3 x4 xy x2y βββββββββββββββββββββββββββββββββββββββ β4 21 16 β64 256 β84 336 β3 12 9 β27 81 β36 108 β2 4 4 β8 16 β8 16 β1 1 1 β1 1 β1 1 0 2 0 0 0 0 0 1 7 1 1 1 7 7 2 15 4 8 16 30 60 3 30 9 27 81 90 270 4 45 16 64 256 180 720 5 67 25 125 625 335 1675 ββββββββββββββββββββββββββββββββββββββ 5 204 85 125 1333 513 319 ββββββββββββββββββββββββββββββββββββββ Remaining d d1 d2 d3 c0 c1 c3 β¦to be done by user
- 10. Flowchart: Curve Fitting (Parabola) s1=sum(x); s2=sum(x.^2); s3=sum(x.^3); s4=sum(x.^4); s5=sum(y); s6=sum(x.*y); s7=sum((x.^2).*y); Calculation of Determinents d, d1, d2 c0=d1/d; c1=d2/d; c2=d3/d; Start Break Read x(i), y(i) For ( i=1 to n) Read n yf=c0+c1*x+c2*x.^2 Print C0, C1, C2 plot(x,y)
- 11. Numerical Power For the power equation: PV^gamma =C P=[0.5 1 1.5 2 2.5 3]; V=[1.62 1 0.75 0.62 0.52 0.46]; Solution: Log(P)+ gamma*log(V)=log(C) Log(P)= log(C) - gamma *log(V) Y = C0 + C1 (X) C0=log(c) C1=-gamma Y=Log(P) X=Log(V) ------------------------------------------------------------------- V P X Y X^2 XY ------------------------------------------------------------------- 1.62 0.5 0.482426 -0.693147 0.232735 -0.334392 1.0 1.0 0. 0. 0. 0. 0.75 1.5 -0.287682 0.405465 0.082761 -0.116645 0.62 2. -0.478036 0.693147 0.228518 -0.331349 0.52 2.5 -0.653926 0.916291 0.427620 -0.599187 0.46 3. -0.776529 1.098612 0.602997 -0.853104 ----------------------------------------------------------- S1= -1.7137 S3=2.4204 S2=1.5746 S4=-2.2347 d = 6.5109 d1 =-0.0185 d2 = -9.2602 c0 =-0.0028 c1 = -1.4223 c = exp(c0)= 0.9972 gamma =-c1=1.4223 PV^1.422=0.997165
- 12. Program Power clc clear all %βββββββββββββPower Equationβββββββββββ %PV^Gamma=C p=[0.5 1.0 1.5 2.0 2.5 3.0]; v=[1.62 1.0 0.75 0.62 0.52 0.46]; n=6; y=log10(p); x=log10(v); xy=x.*y; x2=x.^2; s1=sum(x); s2=sum(x2); s3=sum(y); s4=sum(xy); %ββββββββββββββββββββββββββββββββββββββββββββ d=n*s2βs1*s1; d1=s3*s2βs4*s1; d2=n*s4βs1*s3; %ββββββββββββββββββββββββββββββββββββββββββββ c0=d1/d; c1=d2/d; gamma=βc1; c=exp(c0); %ββββββββββββββββββββββββββββββββββββββββββββ fprintf('PV^%0.3f=%fn',gamma,c) %ββββββββββββββββββββββββββββββββββββββββββββ %plot(p,v); for i=1:n fprintf('%f %f %f %f %f %f n',v(i),p(i),x(i),y(i),x2(i),xy(i)); end
- 13. Numerical Exponential For the Exponential equation: y=aebx x=[2 4 6 8]; y=[25 38 56 84]; Solution y=aebx ln(y)=ln(a)+bx ln(e) Y =C0 +C1(x) yn=ln(y) C0=ln(a) C1=b ------------------------------------------------------ x y yn x^2 x*yn ------------------------------------------------------ 2. 25. 3.218876 4. 6.437752 4. 38. 3.637586 16. 14.550345 6. 56. 4.025352 36. 24.152110 8. 84. 4.430817 64. 35.446534 ----------------------------------------------------- S1=20 s3= 15.3126 s2= 120 s4=80.5867 d = 80 d1 = 225.7808 d2 = 16.0944 c0=2.8223 c1=0.2012 a=exp(c0)= 16.8148 b = c1=0.2012 y=16.815 e (0.2012x)
- 14. Program Exponential clc clear all %βββββββββββββExponentialβββββββββββ %y=ae^bx %ββββββββββββββββββββββββββββββββββββββββββββ x=[2 4 6 8]; y=[25 38 56 84]; n=length(x); %ββββββββββββββββββββββββββββββββββββββββββββ y1=log(y); %ββββββββββββββββββββββββββββββββββββββββββββ x2=x.^2; xy1=x.*y1; s1=sum(x); s2=sum(x2); s3=sum(y1); s4=sum(xy1); %ββββββββββββββββββββββββββββββββββββββββββββ d=n*s2βs1*s1; d1=s3*s2βs4*s1; d2=n*s4βs1*s3; %ββββββββββββββββββββββββββββββββββββββββββββ c0=d1/d; c1=d2/d; a=exp(c0); b=c1; %ββββββββββββββββββββββββββββββββββββββββββββ fprintf('y=%0.3f e^(%0.3fx)n',a,b) %ββββββββββββββββββββββββββββββββββββββββββββ for i=1:n fprintf('%f %f %f %f %f n',x(i),y(i),y1(i),x2(i),xy1(i)); end
- 15. Solver :% POLYFIT clear all x=[19 25 30 36 40 45 50]; y=[76 77 79 80 82 83 85]; d=1; %d=1 (line) d=2(parabola) c=polyfit(x,y,d) % yn = polyval(c, x); yn=c(2)+c(1)*x; plot(x,y,'*',x,yn)



![% LINE FITTING Yf=C0+C1(X)
clc
clear all
%-------------Direct input of Data-----------
x=[1 2 3 4];
y=[2 6 12 20];
n=length(x)
%--------------OR-User UInput of data-----
% n=input('Enter n=');
% for i=1:n
% fprintf('Enter x(%d)=',i);
% x(i)=input('');
% fprintf('Enter y(%d)=',i);
% y(i)=input('');
% end
%--------------------------------------------
s1=sum(x); s2=sum(x.^2); s3=sum(y);
s4=sum(x.*y);
%--------------------------------------------
d=[n s1;
s1 s2];
d1=[s3 s1;
s4 s2];
d2=[n s3;
s1 s4];
d=det(d); d1=det(d1); d2=det(d2);
%--------------------------------------------
c0=d1/d; c1=d2/d;
fprintf('BEST FIT ,Yn=%0.3f+%0.3f(X)n',c0,c1)
%--------------------------------------------
yn=c0+c1*x;
plot(x,y,'*',x,yn)
%--------------------------------------------](https://image.slidesharecdn.com/3-230606051705-346145cd/85/3-pdf-4-320.jpg)
![Solved Problems
Fit the line yn=c0+c1*x
x=[1 2 3 4];
y=[2 6 12 20];
βββββββββββββββββ
X Y X2
XY
βββββββββββββββββ
1 2 1 2
2 6 4 12
3 12 9 36
4 20 16 80
βββββββββββββββββ
10 40 30 130
Calculate d d1 d2 c 0 c1 by you
BEST FIT ,Yn=β5.000+6.000(X)
Fit the line yn=c0+c1*x
L=a0+a1T
x=[ 20 30 40 50 60 70];
y=[800.3 800.4 800.6 800.7 800.9 801];
βββββββββββββββββββββββ
X Y X2
X.*Y
βββββββββββββββββββββββ
20 800 400 16006
30 800 900 24012
40 801 1600 32024
50 801 2500 40035
60 801 3600 48054
70 801 4900 56070
βββββββββββββββββββββββββββββ
270 4804 13900 216201
βββββββββββββββββββββββββββββ
Calculate d d1 d2 c 0 c1 by you](https://image.slidesharecdn.com/3-230606051705-346145cd/85/3-pdf-5-320.jpg)


![Program
% Quadratic FITTING Yf=C0+C1(X)+C2(x^2);
% Quadratic FITTING Yf=C0+C1(X)+C2(x^2);
clc
clear all
%ββββββββββββββββββββββββββββββββββββββββββββββββββββββ
x=[1 2 3 4 5 6 7 8 9];
y=[2 6 7 8 10 11 11 10 9];
n=9;
%ββββββββββββββββββββββββββββββββββββββββββββββββββββββ
x2=x.^2; x3=x.^3; x4=x.^4; xy=x.*y; x2y=(x.^2).*y;
s1=sum(x); s2=sum(x2); s3=sum(x3); s4=sum(x4); s5=sum(y); s6=sum(xy); s7=sum(x2y);
%ββββββββββββββββββββββββββββββββββββββββββββββββββββββ
d=[n s1 s2;
s1 s2 s3
s2 s3 s4];
d1=[s5 s1 s2;
s6 s2 s3
s7 s3 s4];
d2=[n s5 s2;
s1 s6 s3
s2 s7 s4];
d3=[n s1 s5;
s1 s2 s6
s2 s3 s7];
%ββββββββββββββββββββββββββββββββββββββββββββββββββββββ
d=det(d); d1=det(d1); d2=det(d2); d3=det(d3); c0=d1/d; c1=d2/d; c2=d3/d;
%ββββββββββββββββββββββββββββββββββββββββββββββββββββββ
fprintf('BEST FIT ,Yn=%0.3f+%0.3f(X)+%0.3f(x^2)n',c0,c1,c2)
%ββββββββββββββββββββββββββββββββββββββββββββββββββββββ
yn=c0+c1*x+c2*x2;
plot(x,y,'*',x,yn,'r')
%ββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββ
Option
for i=1:n
fprintf('%0.0f %0.0f %0.0f %0.0f %0.0f %0.0f %0.0f
n',x(i),y(i),x2(i),x3(i),x4(i),xy(i),x2y(i))
end
fprintf('ββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββββ
n');
fprintf('%0.0f %0.0f %0.0f %0.0f %0.0f %0.0f %0.0f n',s1,
s5,s2,s3,s4,s6,s7)](https://image.slidesharecdn.com/3-230606051705-346145cd/85/3-pdf-8-320.jpg)
![Solved Problem
Fit the following quadratic/2nd
degree/ parabolic curve + (X) + (X)2
x=[β4 β3 β2 β1 0 1 2 3 4 5];
y=[21 12 4 1 2 7 15 30 45 67];
βββββββββββββββββββββββββββββββββββββββ
X Y x2 x3 x4 xy x2y
βββββββββββββββββββββββββββββββββββββββ
β4 21 16 β64 256 β84 336
β3 12 9 β27 81 β36 108
β2 4 4 β8 16 β8 16
β1 1 1 β1 1 β1 1
0 2 0 0 0 0 0
1 7 1 1 1 7 7
2 15 4 8 16 30 60
3 30 9 27 81 90 270
4 45 16 64 256 180 720
5 67 25 125 625 335 1675
ββββββββββββββββββββββββββββββββββββββ
5 204 85 125 1333 513 319
ββββββββββββββββββββββββββββββββββββββ
Remaining d d1 d2 d3 c0 c1 c3 β¦to be done by user](https://image.slidesharecdn.com/3-230606051705-346145cd/85/3-pdf-9-320.jpg)

![Numerical Power
For the power equation: PV^gamma
=C
P=[0.5 1 1.5 2 2.5 3];
V=[1.62 1 0.75 0.62 0.52 0.46];
Solution: Log(P)+ gamma*log(V)=log(C)
Log(P)= log(C) - gamma *log(V)
Y = C0 + C1 (X)
C0=log(c) C1=-gamma Y=Log(P) X=Log(V)
-------------------------------------------------------------------
V P X Y X^2 XY
-------------------------------------------------------------------
1.62 0.5 0.482426 -0.693147 0.232735 -0.334392
1.0 1.0 0. 0. 0. 0.
0.75 1.5 -0.287682 0.405465 0.082761 -0.116645
0.62 2. -0.478036 0.693147 0.228518 -0.331349
0.52 2.5 -0.653926 0.916291 0.427620 -0.599187
0.46 3. -0.776529 1.098612 0.602997 -0.853104
-----------------------------------------------------------
S1= -1.7137 S3=2.4204 S2=1.5746 S4=-2.2347
d = 6.5109 d1 =-0.0185 d2 = -9.2602
c0 =-0.0028 c1 = -1.4223
c = exp(c0)= 0.9972 gamma =-c1=1.4223
PV^1.422=0.997165](https://image.slidesharecdn.com/3-230606051705-346145cd/85/3-pdf-11-320.jpg)
![Program Power
clc
clear all
%βββββββββββββPower Equationβββββββββββ
%PV^Gamma=C
p=[0.5 1.0 1.5 2.0 2.5 3.0];
v=[1.62 1.0 0.75 0.62 0.52 0.46];
n=6;
y=log10(p);
x=log10(v);
xy=x.*y;
x2=x.^2;
s1=sum(x); s2=sum(x2); s3=sum(y); s4=sum(xy);
%ββββββββββββββββββββββββββββββββββββββββββββ
d=n*s2βs1*s1;
d1=s3*s2βs4*s1;
d2=n*s4βs1*s3;
%ββββββββββββββββββββββββββββββββββββββββββββ
c0=d1/d; c1=d2/d;
gamma=βc1;
c=exp(c0);
%ββββββββββββββββββββββββββββββββββββββββββββ
fprintf('PV^%0.3f=%fn',gamma,c)
%ββββββββββββββββββββββββββββββββββββββββββββ
%plot(p,v);
for i=1:n
fprintf('%f %f %f %f %f %f
n',v(i),p(i),x(i),y(i),x2(i),xy(i));
end](https://image.slidesharecdn.com/3-230606051705-346145cd/85/3-pdf-12-320.jpg)
![Numerical Exponential
For the Exponential equation: y=aebx
x=[2 4 6 8];
y=[25 38 56 84];
Solution
y=aebx
ln(y)=ln(a)+bx ln(e)
Y =C0 +C1(x)
yn=ln(y) C0=ln(a) C1=b
------------------------------------------------------
x y yn x^2 x*yn
------------------------------------------------------
2. 25. 3.218876 4. 6.437752
4. 38. 3.637586 16. 14.550345
6. 56. 4.025352 36. 24.152110
8. 84. 4.430817 64. 35.446534
-----------------------------------------------------
S1=20 s3= 15.3126 s2= 120 s4=80.5867
d = 80 d1 = 225.7808 d2 = 16.0944
c0=2.8223 c1=0.2012
a=exp(c0)= 16.8148 b = c1=0.2012
y=16.815 e (0.2012x)](https://image.slidesharecdn.com/3-230606051705-346145cd/85/3-pdf-13-320.jpg)
![Program Exponential
clc
clear all
%βββββββββββββExponentialβββββββββββ
%y=ae^bx
%ββββββββββββββββββββββββββββββββββββββββββββ
x=[2 4 6 8];
y=[25 38 56 84];
n=length(x);
%ββββββββββββββββββββββββββββββββββββββββββββ
y1=log(y);
%ββββββββββββββββββββββββββββββββββββββββββββ
x2=x.^2; xy1=x.*y1;
s1=sum(x); s2=sum(x2); s3=sum(y1); s4=sum(xy1);
%ββββββββββββββββββββββββββββββββββββββββββββ
d=n*s2βs1*s1;
d1=s3*s2βs4*s1;
d2=n*s4βs1*s3;
%ββββββββββββββββββββββββββββββββββββββββββββ
c0=d1/d; c1=d2/d;
a=exp(c0);
b=c1;
%ββββββββββββββββββββββββββββββββββββββββββββ
fprintf('y=%0.3f e^(%0.3fx)n',a,b)
%ββββββββββββββββββββββββββββββββββββββββββββ
for i=1:n
fprintf('%f %f %f %f %f n',x(i),y(i),y1(i),x2(i),xy1(i));
end](https://image.slidesharecdn.com/3-230606051705-346145cd/85/3-pdf-14-320.jpg)
![Solver :% POLYFIT
clear all
x=[19 25 30 36 40 45 50];
y=[76 77 79 80 82 83 85];
d=1; %d=1 (line) d=2(parabola)
c=polyfit(x,y,d)
% yn = polyval(c, x);
yn=c(2)+c(1)*x;
plot(x,y,'*',x,yn)](https://image.slidesharecdn.com/3-230606051705-346145cd/85/3-pdf-15-320.jpg)