More Related Content Viewers also liked (7)
PPT
Antivormiline kunst
kiuk Ь§
DOC
10kl 7teema gatavoshanaas_ieskaitei
Drakles Ь§
PPTX
ArФni. Autore: Sandra BФrziХa
Drakles Ь§
PPT
AkmeХogles. Autore: Egita KuzХeca
Drakles Ь§
Recently uploaded (10) PPTX
ЮЃЯЮЮДЮЙЮП_ЮЯЮЌЯЮЗЯ_ЮЮБЮЛЮЗЮМЮЯЮБ_Ю ЮБЮЙЮДЮЙЮЌ. ЮЮЛЮЕЯЮИЮЕЯЮЗ ЮЮБЮНЮЕЮЙЯЯЮЙЮКЮЎ ЮЮЙЮВЮЛЮЙЮПЮИЮЎЮКЮЗ.pptx
kalimerapaidia Ь§
PDF
Econometric Methods With Applications In Business And Economics Heij
chunksramudu Ь§
DOCX
APOTELESMATA PANELLINIES 2025 ANTISTOIXIES SXOLON.docx
ssuserf9afe7 Ь§
PPSX
Ю ЮПЮЛЮЙЯЮЙЯЯЮЙЮКЯ ЯЯЯЮГЯЮБЮМЮМЮБ ЯЯ. ЮЯЮПЯ
Я 2024-2025
1lykeioperamatos Ь§
DOCX
ЮЮЕЯЮЕЮГЮГЯЮБЯЮЯ: ЮЮЙ ЮБЮНЯЮЙЯЯЮПЮЙЯЮЏЮЕЯ ЯЯЮН ЯЮМЮЗЮМЮЌЯЯЮН ЯЯЮН ЮЮЮ
Newsroom8 Ь§
1. ЮЮЕЯЮЌЮЛЮБЮЙЮП 4 : ЮЄЮЕЯЮНЮЙЮКЮЯ ЮЃЯЮЕЮДЮЏЮБЯЮЗЯ ЮЮЛЮГЮПЯЮЏЮИЮМЯЮН
т ЮЮНЮЌЮЛЯ
ЯЮЗ Ю ЯЮПЮВЮЛЮЗЮМЮЌЯЯЮН
т ЮЮЮИЮПЮДЮПЮЙ ЮЃЯЮЕЮДЮЏЮБЯЮЗЯ ЮЮЛЮГЮПЯЮЏЮИЮМЯЮН
т ЮЮЮИЮПЮДЮПЯ ЮЮЙЮБЮЏЯЮЕЮЙ ЮКЮБЮЙ ЮЮБЯЮЏЮЛЮЕЯ
ЮЕ
2. ЮЮЕЯЮЌЮЛЮБЮЙЮП 4 : ЮЄЮЕЯЮНЮЙЮКЮЯ ЮЃЯЮЕЮДЮЏЮБЯЮЗЯ ЮЮЛЮГЮПЯЮЏЮИЮМЯЮН
ЮЮЙЮДЮБЮКЯЮЙЮКЮПЮЏ ЯЯЯЯЮПЮЙ ЮКЮЕЯЮБЮЛЮБЮЏЮПЯ
т ЮНЮБ ЯЮЕЮКЮМЮЗЯЮЙЯЮИЮЕЮЏ ЮЗ ЮБЮНЮБЮГЮКЮБЮЙЯЯЮЗЯЮБ ЮБЮНЮЌЮЛЯ
ЯЮЗЯ ЯЮПЯ
ЯЯЮПЮВЮЛЮЎЮМЮБЯЮПЯ ЮКЮБЮЙ ЯЮЗЯ ЯЯЮЕЮДЮЏЮБЯЮЗЯ ЯЮПЯ
ЮКЮБЯЮЌЮЛЮЛЮЗЮЛЮПЯ
ЮБЮЛЮГЮПЯЮЏЮИЮМЮПЯ
,
т ЮНЮБ ЮМЯЮПЯЮЕЮЏ ЮНЮБ ЯЯЮЕЮДЮЙЮБЯЮИЮЕЮЏ ЮЮНЮБЯ ЮБЮЛЮГЯЯЮЙЮИЮМЮПЯ ЯЯ ЮМЮЏЮБ
ЮБЮКЮПЮЛЮПЯ
ЮИЮЏЮБ ЮВЮЗЮМЮЌЯЯЮН
т ЮНЮБ ЮИЮЕЯЯЮЗЮИЮПЯЮН ЮМЮЕЯЮЙЮКЮЯ ЮПЮЙЮКЮПЮГЮЮНЮЕЮЙЮЕЯ ЯЯЮЕЮДЮЙЮБЯЮМЮПЯ
ЮБЮЛЮГЮПЯЮЏЮИЮМЯЮН
3. ЮЮЕЯЮЌЮЛЮБЮЙЮП 4 : ЮЄЮЕЯЮНЮЙЮКЮЯ ЮЃЯЮЕЮДЮЏЮБЯЮЗЯ ЮЮЛЮГЮПЯЮЏЮИЮМЯЮН
ЮЮНЮЌЮЛЯ
ЯЮЗ Ю ЯЮПЮВЮЛЮЗЮМЮЌЯЯЮН
ЮЮБЯЮЌ ЯЮЗЮН ЮБЮНЮЌЮЛЯ
ЯЮЗ ЮЕЮНЯЯ ЯЯЮПЮВЮЛЮЎЮМЮБЯЮПЯ
т ЮКЮБЯЮБЮГЯЮЌЯЮЕЯЮБЮЙ ЮЗ Я
ЯЮЌЯЯЮПЯ
ЯЮБ ЯЮЛЮЗЯЮПЯЮПЯЮЏЮБ,
т ЮБЮНЮБЮГЮНЯЯЮЏЮЖЮПЮНЯЮБЮЙ ЮЙЮДЮЙЮБЮЙЯЮЕЯЯЯЮЗЯЮЕЯ,
т ЮБЯЮПЯЯ
ЯЯЮНЮПЮНЯЮБЮЙ ЯЯ
ЮНЮИЮЎЮКЮЕЯ ЮКЮБЮЙ ЯЯЮПЯЯЮПЮИЮЯЮЕЮЙЯ,
ЮПЯЯЯЮЕ
т ЯЯЮПЯЮЕЮЏЮНЮЕЯЮБЮЙ ЮКЮЌЯЮПЮЙЮБ ЮМЮЮИЮПЮДЮПЯ (ЮЙЮДЮЕЮБЯЮЎ), ЮКЮБЮЙ
т ЮЕЯЮЙЮЛЯЮЕЯЮБЮЙ ЯЮП ЯЯЯЮВЮЛЮЗЮМЮБ ЮМЮЕ ЯЮПЮН Я
ЯЮПЮЛЮПЮГЮЙЯЯЮЎ.
4. ЮЮЕЯЮЌЮЛЮБЮЙЮП 4 : ЮЄЮЕЯЮНЮЙЮКЮЯ ЮЃЯЮЕЮДЮЏЮБЯЮЗЯ ЮЮЛЮГЮПЯЮЏЮИЮМЯЮН
ЮЮНЮЌЮЛЯ
ЯЮЗ Ю ЯЮПЮВЮЛЮЗЮМЮЌЯЯЮН
Ю ЯЯЮВЮЛЮЗЮМЮБ: ЮМЮЕ ЯЮПЮЙЮЌ ЯЮЕЮЙЯЮЌ ЯЯЮЯЮЕЮЙ ЮЮНЮБЯ
ЯЮБЯЯ
ЮДЯЮПЮМЮЙЮКЯЯ ЮДЮЙЮБЮНЮПЮМЮЮБЯ ЮНЮБ ЮЕЯЮЙЯЮКЮЕЯЮИЮЕЮЏ
ЮКЮЌЯЮПЮЙЮБ ЯЯЯЮЙЮЌ ЯЯЯЮЕ ЮНЮБ ЮЕЮЛЮБЯЮЙЯЯЮПЯЮПЮЙЮЎЯЮЕЮЙ ЯЮЗ
ЯЯ
ЮНЮПЮЛЮЙЮКЮЎ ЮБЯЯЯЯЮБЯЮЗ ЯЮПЯ
ЮИЮБ ЮДЮЙЮБЮНЯЯЮЕЮЙ ??
Ю ЮЙЮИЮБЮНЮЯ ЮЛЯЯЮЕЮЙЯ
т ЮКЮЌЮИЮЕ ЯЮПЯЮЌ ЮНЮБ ЮДЮЙЮБЮЛЮЮГЮЕЮЙ ЯЮПЮН ЮКЮПЮНЯЮЙЮНЯЯЮЕЯЮП ЯЯЮПЮПЯЮЙЯЮМЯ
т ЮНЮБ ЮБЮКЮПЮЛЮПЯ
ЮИЮЎЯЮЕЮЙ ЮЮНЮБ ЮДЯЮПЮМЮПЮЛЯЮГЮЙЮП ЯЮПЯ
ЮНЮБ
ЮЕЮЛЮБЯЮЙЯЯЮПЯЮПЮЙЮЕЮЏ ЯЮЗ ЯЯ
ЮНЮПЮЛЮЙЮКЮЎ ЮБЯЯЯЯЮБЯЮЗ ЮКЮБЮЙ ЯЯЮЙ ЯЮЙЯ
ЮЕЯЮЙЮМЮЯЮПЯ
Я.
5. ЮЮЕЯЮЌЮЛЮБЮЙЮП 4 : ЮЄЮЕЯЮНЮЙЮКЮЯ ЮЃЯЮЕЮДЮЏЮБЯЮЗЯ ЮЮЛЮГЮПЯЮЏЮИЮМЯЮН
ЮЮЮИЮПЮДЮПЮЙ ЮЃЯЮЕЮДЮЏЮБЯЮЗЯ ЮЮЛЮГЮПЯЮЙЮИЮМЯЮН
ЮЮЙ ЮБЮЛЮГЯЯЮЙЮИЮМЮПЮЙ ЮЯЮПЯ
ЮН ЮПЮМЮБЮДЮПЯЮПЮЙЮЗЮИЮЕЮЏ ЮБЮНЮЌЮЛЮПЮГЮБ ЮМЮЕ ЯЮБ
ЮВЮБЯЮЙЮКЮЌ ЯЮПЯ
Я ЯЮБЯЮБЮКЯЮЗЯЮЙЯЯЮЙЮКЮЌ ЯЮЕ ЮДЮЙЮЌЯЮПЯЮЕЯ ЮПЮЙЮКЮПЮГЮЮНЮЕЮЙЮЕЯ.
т ЮЮЮИЮПЮДЮПЯ ЮЮЙЮБЮЏЯЮЕЮЙ ЮКЮБЮЙ ЮЮБЯЮЏЮЛЮЕЯ
ЮЕ
(ЮЯ
ЮБЮДЮЙЮКЮЎ ЮБЮНЮБЮЖЮЎЯЮЗЯЮЗ, ЮМЮЮИЮПЮДЮПЯ ЮДЮЙЯЮПЯЯЮМЮЗЯЮЗЯ-Bolzano)
т ЮЮЮИЮПЮДЮПЯ ЮЯ
ЮНЮБЮМЮЙЮКЮПЯ Ю ЯЮПЮГЯЮБЮМЮМЮБЯЮЙЯЮМЮПЯ
(Я
ЯЮПЮЛЮПЮГЮЙЯЮМЯЯ ЮДЯЮНЮБЮМЮЗЯ: x16)
т ЮЯЮЛЮЗЯЯЮЗ ЮЮЮИЮПЮДЮПЯ
(ЮЗ ЯЯЯЯЮЗ ЯЯЮПЯЮЮГЮГЮЙЯЮЗ ЯЯЮП ЯЯЯЮВЮЛЮЗЮМЮБ ЯЮПЯ
ЯЮБЯЯ
ЮДЯЯЮМЮПЯ
)
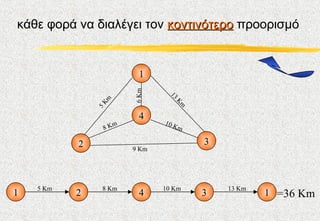
6. ЮКЮЌЮИЮЕ ЯЮПЯЮЌ ЮНЮБ ЮДЮЙЮБЮЛЮЮГЮЕЮЙ ЯЮПЮН ЮКЮПЮНЯЮЙЮНЯЯЮЕЯЮП ЯЯЮПЮПЯЮЙЯЮМЯ
1
6 Km
13
Km
Km
5
4
m 10 K
8K m
2 3
9 Km
5 Km 8 Km 10 Km 13 Km
1 2 4 3 1 =36 Юm
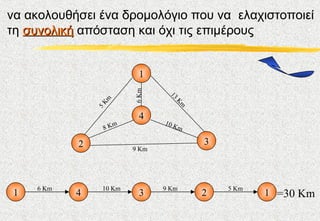
7. ЮНЮБ ЮБЮКЮПЮЛЮПЯ
ЮИЮЎЯЮЕЮЙ ЮЮНЮБ ЮДЯЮПЮМЮПЮЛЯЮГЮЙЮП ЯЮПЯ
ЮНЮБ ЮЕЮЛЮБЯЮЙЯЯЮПЯЮПЮЙЮЕЮЏ
ЯЮЗ ЯЯ
ЮНЮПЮЛЮЙЮКЮЎ ЮБЯЯЯЯЮБЯЮЗ ЮКЮБЮЙ ЯЯЮЙ ЯЮЙЯ ЮЕЯЮЙЮМЮЯЮПЯ
Я
1
6 Km
13
Km
Km
5
4
m 10 K
8K m
2 3
9 Km
6 Km 10 Km 9 Km 5 Km
1 4 3 2 1 =30 Юm