429.–ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ķ –Ņ–ĺ—Ā–ĺ–Ī–ł–Ķ –Ņ–ĺ –ī–ł—Ā—Ü–ł–Ņ–Ľ–ł–Ĺ–Ķ ¬ę–ł–Ĺ—Ą–ĺ—Ä–ľ–į—ā–ł–ļ–į¬Ľ —á2 –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č mathcad
- 1. –ú–ė–Ě–ė–°–Ę–ē–†–°–Ę–í–ě –ě–Ď–†–ź–ó–ě–í–ź–Ě–ė–Į –ė –Ě–ź–£–ö–ė –†–ě–°–°–ė–ô–°–ö–ě–ô –§–ē–Ē–ē–†–ź–¶–ė–ė –§–Ķ–ī–Ķ—Ä–į–Ľ—Ć–Ĺ–ĺ–Ķ –≥–ĺ—Ā—É–ī–į—Ä—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ķ –į–≤—ā–ĺ–Ĺ–ĺ–ľ–Ĺ–ĺ–Ķ –ĺ–Ī—Ä–į–∑–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ķ —É—á—Ä–Ķ–∂–ī–Ķ–Ĺ–ł–Ķ –≤—č—Ā—ą–Ķ–≥–ĺ –Ņ—Ä–ĺ—Ą–Ķ—Ā—Ā–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź ¬ę–°–Ķ–≤–Ķ—Ä–Ĺ—č–Ļ (–ź—Ä–ļ—ā–ł—á–Ķ—Ā–ļ–ł–Ļ) —Ą–Ķ–ī–Ķ—Ä–į–Ľ—Ć–Ĺ—č–Ļ —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā –ł–ľ–Ķ–Ĺ–ł –ú.–í. –õ–ĺ–ľ–ĺ–Ĺ–ĺ—Ā–ĺ–≤–į¬Ľ –ė–Ĺ—Ā—ā–ł—ā—É—ā –≠–Ĺ–Ķ—Ä–≥–Ķ—ā–ł–ļ–ł –ł —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–į –ú–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ķ –Ņ–ĺ—Ā–ĺ–Ī–ł–Ķ –Ņ–ĺ –ī–ł—Ā—Ü–ł–Ņ–Ľ–ł–Ĺ–Ķ ¬ę–ė–Ĺ—Ą–ĺ—Ä–ľ–į—ā–ł–ļ–į¬Ľ —á–į—Ā—ā—Ć 2 –ė—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č Mathcad –ź—Ä—Ö–į–Ĺ–≥–Ķ–Ľ—Ć—Ā–ļ 2014 Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 2. –†–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–į –ł —Ä–Ķ–ļ–ĺ–ľ–Ķ–Ĺ–ī–ĺ–≤–į–Ĺ–į –ļ –ł–∑–ī–į–Ĺ–ł—é –ļ–į—Ą–Ķ–ī—Ä–ĺ–Ļ –Ę—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ–ĺ-—ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł—Ö –ľ–į—ą–ł–Ĺ, –ĺ–Ī–ĺ—Ä—É–ī–ĺ–≤–į–Ĺ–ł—Ź –ł –Ľ–ĺ–≥–ł—Ā—ā–ł–ļ–ł 6 –Ĺ–ĺ—Ź–Ī—Ä—Ź 2014 –≥. –°–ĺ—Ā—ā–į–≤–ł—ā–Ķ–Ľ–ł: –ź.–í. –°—č—Ā–ĺ–Ķ–≤–į, –į—Ā—Ā–ł—Ā—ā–Ķ–Ĺ—ā; –Ę.–ē. –¶–Ķ—Ö–ľ–ł—Ā—ā—Ä–ĺ–≤–į, –į—Ā—Ā–ł—Ā—ā–Ķ–Ĺ—ā; –ú.–í. –ú–Ķ–Ĺ—Ć—ą–ł–ļ–ĺ–≤, –į—Ā—Ā–ł—Ā—ā–Ķ–Ĺ—ā –Ē.–í. –õ–Ķ–Ī–Ķ–ī–Ķ–≤, –į—Ā—Ā–ł—Ā—ā–Ķ–Ĺ—ā –ú.–í. –í–ł—ā—Ź–∑–Ķ–≤, —Ā—ā–į—Ä—ą–ł–Ļ –Ņ—Ä–Ķ–Ņ–ĺ–ī–į–≤–į—ā–Ķ–Ľ—Ć. –ģ.–ú. –õ—É–ļ–ł–Ĺ, —Ā—ā–į—Ä—ą–ł–Ļ –Ņ—Ä–Ķ–Ņ–ĺ–ī–į–≤–į—ā–Ķ–Ľ—Ć –í.–ē. –®–Ķ—Ö—É—Ä–ł–Ĺ, —Ā—ā–į—Ä—ą–ł–Ļ –Ņ—Ä–Ķ–Ņ–ĺ–ī–į–≤–į—ā–Ķ–Ľ—Ć –†–Ķ—Ü–Ķ–Ĺ–∑–Ķ–Ĺ—ā –ú.–ģ. –ú–į—Ä—É—ą–ļ–Ķ–Ļ, –ī–ĺ—Ü–Ķ–Ĺ—ā, –ļ–į–Ĺ–ī–ł–ī–į—ā —ā–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł—Ö –Ĺ–į—É–ļ –£–Ē–ö 004 –ú–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ķ –Ņ–ĺ—Ā–ĺ–Ī–ł–Ķ –Ņ–ĺ –ī–ł—Ā—Ü–ł–Ņ–Ľ–ł–Ĺ–Ķ ¬ę–ė–Ĺ—Ą–ĺ—Ä–ľ–į—ā–ł–ļ–į¬Ľ —á–į—Ā—ā—Ć 2 –ė—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č Mathcad/ —Ā–ĺ—Ā—ā–į–≤–ł—ā–Ķ–Ľ–ł: –ź.–í. –°—č—Ā–ĺ–Ķ–≤–į, –Ę.–ē. –¶–Ķ—Ö–ľ–ł—Ā—ā—Ä–ĺ–≤–į, –ú.–í. –ú–Ķ–Ĺ—Ć—ą–ł–ļ–ĺ–≤, –í. –õ–Ķ–Ī–Ķ–ī–Ķ–≤, –ú.–í. –í–ł—ā—Ź–∑–Ķ–≤, –ģ.–ú. –õ—É–ļ–ł–Ĺ, –í.–ē. –®–Ķ—Ö—É—Ä–ł–Ĺ. –ü–ĺ–ī–≥–ĺ—ā–ĺ–≤–Ľ–Ķ–Ĺ–ĺ –ļ–į—Ą–Ķ–ī—Ä–ĺ–Ļ —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–Ĺ–ĺ-—ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł—Ö –ľ–į—ą–ł–Ĺ, –ĺ–Ī–ĺ—Ä—É–ī–ĺ–≤–į–Ĺ–ł—Ź –ł –Ľ–ĺ–≥–ł—Ā—ā–ł–ļ–ł –ł–Ĺ—Ā—ā–ł—ā—É—ā–į —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł–ļ–ł –ł —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–į –í –ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–ľ –Ņ–ĺ—Ā–ĺ–Ī–ł–ł –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–į –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–į—Ź –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź –ī–Ľ—Ź —Ā–į–ľ–ĺ—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ–ĺ–ī–≥–ĺ—ā–ĺ–≤–ļ–Ķ –ļ –Ņ—Ä–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł–ľ –∑–į–Ĺ—Ź—ā–ł—Ź–ľ –Ņ–ĺ —Ä–į–Ī–ĺ—ā–į —Ā —Ā–ł—Ā—ā–Ķ–ľ–ĺ–Ļ Mathcad –ł –≤–į—Ä–ł–į–Ĺ—ā—č –∑–į–ī–į–Ĺ–ł–Ļ –ī–Ľ—Ź –Ľ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ—č—Ö —Ä–į–Ī–ĺ—ā –Ņ–ĺ Mathcad. –ü—Ä–Ķ–ī–Ĺ–į–∑–Ĺ–į—á–Ķ–Ĺ—č –ī–Ľ—Ź —Ā—ā—É–ī–Ķ–Ĺ—ā–ĺ–≤ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–ī–≥–ĺ—ā–ĺ–≤–ļ–ł –Ī–į–ļ–į–Ľ–į–≤—Ä–ĺ–≤ –Ď–ł–Ī–Ľ–ł–ĺ–≥—Ä. 2 ¬© –°–Ķ–≤–Ķ—Ä–Ĺ—č–Ļ (–ź—Ä–ļ—ā–ł—á–Ķ—Ā–ļ–ł–Ļ) —Ą–Ķ–ī–Ķ—Ä–į–Ľ—Ć–Ĺ—č–Ļ —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā –ł–ľ–Ķ–Ĺ–ł –ú.–í. –õ–ĺ–ľ–ĺ–Ĺ–ĺ—Ā–ĺ–≤–į, 2014 Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 3. –í–í–ē–Ē–ē–Ě–ė–ē –Ē–Ľ—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł—Ź —Ā–Ľ–ĺ–∂–Ĺ—č—Ö –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—Ö —Ä–į—Ā—á–Ķ—ā–ĺ–≤ –ł –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –Ĺ–į—É—á–Ĺ—č—Ö –ł–∑—č—Ā–ļ–į–Ĺ–ł–Ļ —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –ł–ľ–Ķ—ā—Ć –Ĺ–į–ī–Ķ–∂–Ĺ—č–Ļ –ł –ľ–Ĺ–ĺ–≥–ĺ–Ņ—Ä–ĺ—Ą–ł–Ľ—Ć–Ĺ—č–Ļ –ł–Ĺ—Ā—ā—Ä—É–ľ–Ķ–Ĺ—ā. Mathcad ‚Äď —ć—ā–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ļ —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä, –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–į—Č–ł–Ļ –ļ–Ľ–į—Ā—Ā—É —Ā–ł—Ā—ā–Ķ–ľ –į–≤—ā–ĺ–ľ–į—ā–ł–∑–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ–Ķ–ļ—ā–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź. –ě–Ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā—Ć —Ä–į—Ā—á–Ķ—ā—č —Ä–į–∑–Ĺ–ĺ–Ļ —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –ł —Ā—ā—Ä–ĺ–ł—ā—Ć –≥—Ä–į—Ą–ł–ļ–ł –ł –ī–ł–į–≥—Ä–į–ľ–ľ—č –Ņ–ĺ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ—č–ľ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į–ľ –≤ –Ņ—Ä–ĺ—Ā—ā–ĺ–ľ –ł –Ņ–ĺ–Ĺ—Ź—ā–Ĺ–ĺ–ľ –≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ĺ–ľ –≤–ł–ī–Ķ. –ó–į–Ņ–ł—Ā—Ć –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ļ –≤ Mathcad –ľ–į–Ľ–ĺ –ĺ—ā–Ľ–ł—á–į–Ķ—ā—Ā—Ź –ĺ—ā –Ņ—Ä–ł–≤—č—á–Ĺ–ĺ–Ļ —Ä—É–ļ–ĺ–Ņ–ł—Ā–Ĺ–ĺ–Ļ –∑–į–Ņ–ł—Ā–ł, —á—ā–ĺ –∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —É—Ā–ļ–ĺ—Ä—Ź–Ķ—ā –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā—č –į–ī–į–Ņ—ā–į—Ü–ł–ł –ł –ĺ—Ā–≤–ĺ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ—č. –í—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –≤ Mathcad –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī—Ź—ā –≤ —Ä–Ķ–∂–ł–ľ–Ķ —Ä–Ķ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł, —á—ā–ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā —Ā—Ä–į–∑—É —É–≤–ł–ī–Ķ—ā—Ć –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–≥–ĺ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į –Ņ–ĺ—Ā–Ľ–Ķ –≤–Ĺ–Ķ—Ā–Ķ–Ĺ–ł—Ź –ļ–ĺ—Ä—Ä–Ķ–ļ—ā–ł—Ä–ĺ–≤–ĺ–ļ, –≤ —ā–ĺ–ľ —á–ł—Ā–Ľ–Ķ –ł –Ĺ–į –≥—Ä–į—Ą–ł–ļ–į—Ö. –í–į–∂–Ĺ–ĺ–Ļ –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć—é —Ā–ł—Ā—ā–Ķ–ľ—č —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ WYSIWYG. –Ď–Ľ–į–≥–ĺ–ī–į—Ä—Ź –Ķ–ľ—É —Ą–ĺ—Ä–ľ—É–Ľ—č, –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ–Ĺ—č–Ļ –ļ–ĺ–ī –ł –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ —ā–Ķ–ļ—Ā—ā–į –Ĺ–į —ć–ļ—Ä–į–Ĺ–Ķ –ľ–ĺ–Ĺ–ł—ā–ĺ—Ä–į –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—é –Ĺ–į –Ľ–ł—Ā—ā–Ķ –Ņ—Ä–ł –Ņ–Ķ—á–į—ā–ł. –≠—ā–ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā—Ć –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ–Ķ –ĺ—Ą–ĺ—Ä–ľ–Ľ–Ķ–Ĺ–ł–Ķ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–ĺ–≤ —Ä–į–Ī–ĺ—ā—č –Ī–Ķ–∑ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–ł—Ö –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ. –¶–Ķ–Ľ—Ć –ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —Ä–į–∑–ī–Ķ–Ľ–į –Ņ–ĺ—Ā–ĺ–Ī–ł—Ź ‚Äď –ī–į—ā—Ć –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ź—Ö –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—Ö —Ä–į—Ā—á–Ķ—ā–ĺ–≤ –ł –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–ł –≥—Ä–į—Ą–ł–ļ–ĺ–≤ –≤ —Ā–ł—Ā—ā–Ķ–ľ–Ķ Mathcad,. –ü–ĺ—Ā–ĺ–Ī–ł–Ķ –ľ–ĺ–∂–Ķ—ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć—Ā—Ź –ī–Ľ—Ź –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ–Ļ –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł–ł –ł –Ņ–ĺ–ī–≥–ĺ—ā–ĺ–≤–ļ–ł –ļ –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł—é –Ľ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ—č—Ö —Ä–į–Ī–ĺ—ā –Ē–į–Ĺ–Ĺ–ĺ–Ķ –ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ķ –Ņ–ĺ—Ā–ĺ–Ī–ł–Ķ –Ņ—Ä–Ķ–ī–Ĺ–į–∑–Ĺ–į—á–Ķ–Ĺ–ĺ –ī–Ľ—Ź –Ī–į–ļ–į–Ľ–į–≤—Ä–ĺ–≤ —ā–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ—Ā—ā–Ķ–Ļ –ė–Ĺ—Ā—ā–ł—ā—É—ā–į —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł–ļ–ł –ł —ā—Ä–į–Ĺ—Ā–Ņ–ĺ—Ä—ā–į. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 4. –°—ā—Ä—É–ļ—ā—É—Ä–į —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ –ĺ–ļ–Ĺ–į Mathcad. –†–į–Ī–ĺ—á–Ķ–Ķ –ĺ–ļ–Ĺ–ĺ –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ—č Mathcad –≤–ļ–Ľ—é—á–į–Ķ—ā –≤ —Ā–Ķ–Ī—Ź: 1. –í–Ķ—Ä—Ö–Ĺ–Ķ–Ķ –ľ–Ķ–Ĺ—é —Ā–ĺ –≤–ļ–Ľ–į–ī–ļ–į–ľ–ł (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 1) –†–ł—Ā—É–Ĺ–ĺ–ļ 1 –í–Ķ—Ä—Ö–Ĺ—Ź—Ź —á–į—Ā—ā—Ć –ĺ–ļ–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ—č Mathcad. 2. –†–į–Ī–ĺ—á—É—é –ĺ–Ī–Ľ–į—Ā—ā—Ć –≤ –≤–ł–ī–Ķ –Ī–Ķ–Ľ–ĺ–≥–ĺ –Ľ–ł—Ā—ā–į, —Ä–į–∑–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į –ĺ–Ī–Ľ–į—Ā—ā–ł –Ņ–ĺ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—É –Ņ–Ķ—á–į—ā–ł. 3. –°—ā—Ä–ĺ–ļ–į —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 2) –†–ł—Ā—É–Ĺ–ĺ–ļ 2 –°—ā—Ä–ĺ–ļ–į —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –í–į–∂–Ĺ–ĺ–Ļ —á–į—Ā—ā—Ć—é –≤–Ķ—Ä—Ö–Ĺ–Ķ–≥–ĺ –ľ–Ķ–Ĺ—é —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–į–Ĺ–Ķ–Ľ—Ć ¬ę–ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł¬Ľ (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 3) –†–ł—Ā—É–Ĺ–ĺ–ļ 3 –ü–į–Ĺ–Ķ–Ľ—Ć ¬ę–ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—謼 –≠—ā–į –Ņ–į–Ĺ–Ķ–Ľ—Ć —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ –ł–Ĺ—Ā—ā—Ä—É–ľ–Ķ–Ĺ—ā—č, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—č–Ķ –Ņ—Ä–ł —Ä–į–Ī–ĺ—ā–Ķ —Ā –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ–ĺ–Ļ (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 4): Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 5. –†–ł—Ā—É–Ĺ–ĺ–ļ 4 –ě–ļ–Ĺ–ĺ Mathcad —Ā–ĺ –≤—Ā–Ķ–ľ–ł –Ņ–į–Ľ–ł—ā—Ä–į–ľ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—Ö –∑–Ĺ–į–ļ–ĺ–≤ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 6. –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į 23 –†–Ķ—ą–Ķ–Ĺ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ MathCad. –ü—Ä–ł–ľ–Ķ—Ä: –Ē–į–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ –≤–ł–ī–į ÔÉĮ ÔÉĮ ÔÉģ ÔÉĮ ÔÉĮ ÔÉ≠ Ôɨ ÔÄĹÔÄęÔÉóÔÄęÔÄęÔÉó ÔÄĹÔÉóÔÄęÔÄęÔÄę ÔÄĹÔÉóÔÄ≠ÔÉóÔÄ≠ÔÄ≠ÔÉó ÔÄĹÔÉóÔÄęÔÉóÔÄ≠ÔÉóÔÄęÔÉó 421.0 81.0 3323 62432 dcba dcba dcba dcba 1. –†–Ķ—ą–Ķ–Ĺ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ –ľ–į—ā—Ä–ł—á–Ĺ—č–ľ –ľ–Ķ—ā–ĺ–ī–ĺ–ľ –ü—Ä–ł —ć—ā–ĺ–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ķ –Ĺ–į–ľ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ —Ā–ĺ—Ā—ā–į–≤–ł—ā—Ć 2 –ľ–į—ā—Ä–ł—Ü—č –ź –ł –í. –ú–į—ā—Ä–ł—Ü–į –ź –Ī—É–ī–Ķ—ā —Ā–ĺ–ī–Ķ—Ä–∂–į—ā—Ć –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č –Ņ–Ķ—Ä–Ķ–ī –Ĺ–Ķ–ł–∑–≤–Ķ—Ā—ā–Ĺ—č–ľ–ł, –į –ľ–į—ā—Ä–ł—Ü–į –í ‚Äď —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā—č, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ī–ĺ–Ľ–∂–Ĺ—č –Ņ–ĺ–Ľ—É—á–į—é—ā—Ā—Ź –≤ —Ä–į—Ā—á–Ķ—ā–į—Ö (—Ā–≤–ĺ–Ī–ĺ–ī–Ĺ—č–Ķ —á–Ľ–Ķ–Ĺ—č). –†–Ķ—ą–į–Ķ–ľ —Ā–ł—Ā—ā–Ķ–ľ—É —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ BAL ÔÉóÔÄĹ ÔÄ≠1 : –Ě–į —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ —Ā—ā—Ä–ĺ—á–ļ–Ķ —Ā—ā–į–≤–ł–ľ –Ī—É–ļ–≤—É L –ł –Ĺ–į–∂–ł–ľ–į–Ķ–ľ –ļ–Ĺ–ĺ–Ņ–ļ—É ¬ę=¬Ľ –Ĺ–į –ļ–Ľ–į–≤–ł–į—ā—É—Ä–Ķ. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 7. 2. –†–Ķ—ą–Ķ–Ĺ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ –ľ–į—ā—Ä–ł—á–Ĺ—č–ľ –ľ–Ķ—ā–ĺ–ī–ĺ–ľ —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ lsolve. –ü—Ä–ł —ć—ā–ĺ–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ķ –Ĺ–į–ľ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ —Ā–ĺ—Ā—ā–į–≤–ł—ā—Ć 2 –ľ–į—ā—Ä–ł—Ü—č –ź –ł –í. –ú–į—ā—Ä–ł—Ü–į –ź –Ī—É–ī–Ķ—ā —Ā–ĺ–ī–Ķ—Ä–∂–į—ā—Ć –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č –Ņ–Ķ—Ä–Ķ–ī –Ĺ–Ķ–ł–∑–≤–Ķ—Ā—ā–Ĺ—č–ľ–ł, –į –ľ–į—ā—Ä–ł—Ü–į –í ‚Äď —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā—č, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ī–ĺ–Ľ–∂–Ĺ—č –Ņ–ĺ–Ľ—É—á–į—é—ā—Ā—Ź –≤ —Ä–į—Ā—á–Ķ—ā–į—Ö (—Ā–≤–ĺ–Ī–ĺ–ī–Ĺ—č–Ķ —á–Ľ–Ķ–Ĺ—č). –ü–ĺ—Ā–Ľ–Ķ —ć—ā–ĺ–≥–ĺ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –• –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ņ—Ä–ł—Ā–≤–ĺ–ł—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ lsolve(A,B) –ł –Ņ–ĺ—Ā–ľ–ĺ—ā—Ä–Ķ—ā—Ć –Ķ—ź –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ: –ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł–Ķ –ě–Ī—Ä–į—ā–ł—ā–Ķ –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ, —á—ā–ĺ –ī–Ľ—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź —ā–į–ļ–ł–ľ–ł —Ā–Ņ–ĺ—Ā–ĺ–Ī–į–ľ–ł –Ĺ–Ķ—ā –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā–ł –∑–į–Ņ–ł—Ā—č–≤–į—ā—Ć —Ā–į–ľ–ł –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 8. 3. –†–Ķ—ą–Ķ–Ĺ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ —Ā–≤—Ź–∑–ļ–ł Given ‚Äď Find –Ē–Ľ—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź —ć—ā–ł–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ, –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ņ–Ķ—Ä–Ķ–Ņ–ł—Ā–į—ā—Ć –Ķ–≥–ĺ –≤ —Ā—Ä–Ķ–ī–Ķ MathCad, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –≤–ľ–Ķ—Ā—ā–ĺ –∑–Ĺ–į–ļ–ĺ–≤ = —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ļ –∑–Ĺ–į–ļ , –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –≤ –Ņ–į–Ĺ–Ķ–Ľ–Ķ –ł–Ĺ—Ā—ā—Ä—É–ľ–Ķ–Ĺ—ā–ĺ–≤ –Ď—É–Ľ–Ķ–≤–į—Ź –į–Ľ–≥–Ķ–Ī—Ä–į. –Ě–į–ī —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ–ľ –Ĺ—É–∂–Ĺ–ĺ –Ĺ–į–Ņ–ł—Ā–į—ā—Ć –ļ–ĺ–ľ–į–Ĺ–ī—É Given, –į –≤—č—ą–Ķ –Ķ–Ķ –∑–į–ī–į—ā—Ć –Ĺ–į—á–į–Ľ—Ć–Ĺ—č–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö –≤ –Ĺ–Ķ–ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—č—Ö, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä 0. –ü–ĺ—Ā–Ľ–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –∑–į–Ņ–ł—ą–Ķ–ľ –ļ–ĺ–ľ–į–Ĺ–ī—É Find(a,b,c,d) –ł –Ĺ–į–∂–ľ–Ķ–ľ –ļ–Ĺ–ĺ–Ņ–ļ—É ¬ę=¬Ľ –Ĺ–į –ļ–Ľ–į–≤–ł–į—ā—É—Ä–Ķ: Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 9. 4. –†–Ķ—ą–Ķ–Ĺ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ —Ā–≤—Ź–∑–ļ–ł Given ‚Äď Minerr –Ē–Ľ—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź —ć—ā–ł–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ, –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ņ–Ķ—Ä–Ķ–Ņ–ł—Ā–į—ā—Ć –Ķ–≥–ĺ –≤ —Ā—Ä–Ķ–ī–Ķ MathCad, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –≤–ľ–Ķ—Ā—ā–ĺ –∑–Ĺ–į–ļ–ĺ–≤ = —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ļ –∑–Ĺ–į–ļ , –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –≤ –Ņ–į–Ĺ–Ķ–Ľ–Ķ –ł–Ĺ—Ā—ā—Ä—É–ľ–Ķ–Ĺ—ā–ĺ–≤ –Ď—É–Ľ–Ķ–≤–į—Ź –į–Ľ–≥–Ķ–Ī—Ä–į. –Ě–į–ī —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ–ľ –Ĺ—É–∂–Ĺ–ĺ –Ĺ–į–Ņ–ł—Ā–į—ā—Ć –ļ–ĺ–ľ–į–Ĺ–ī—É Given, –į –≤—č—ą–Ķ –Ķ–Ķ –∑–į–ī–į—ā—Ć –Ĺ–į—á–į–Ľ—Ć–Ĺ—č–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö –≤ –Ĺ–Ķ–ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—č—Ö, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä 0. –Ē–Ľ—Ź –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł—Ź –Ī–ĺ–Ľ–Ķ–Ķ —ā–ĺ—á–Ĺ—č—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ, –ļ–ĺ–ľ–į–Ĺ–ī–į Minerr(a,b,c,d) –Ņ—Ä–ł—Ā–≤–į–ł–≤–į–Ķ—ā—Ā—Ź –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ k. –Ě–į —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ —Ā—ā—Ä–ĺ—á–ļ–Ķ –Ņ–ĺ—Ā–Ľ–Ķ k —Ā—ā–į–≤–ł–ľ —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ļ –∑–Ĺ–į–ļ ‚Üí –ł –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł–Ļ. –ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł–Ķ. –°—ā–ĺ–ł—ā –ĺ—ā–ľ–Ķ—ā–ł—ā—Ć, —á—ā–ĺ —ā–į–ļ–ł–ľ –∂–Ķ –ĺ–Ī—Ä–į–∑–ĺ–ľ –ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ–Ľ—É—á–ł—ā—Ć —É—ā–ĺ—á–Ĺ–Ķ–Ĺ–Ĺ—č–Ļ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā –ļ–ĺ–ľ–į–Ĺ–ī–ĺ–Ļ Find: –ė –Ĺ–į–ĺ–Ī–ĺ—Ä–ĺ—ā ‚Äď –Ņ–ĺ–Ľ—É—á–ł—ā—Ć —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā —Ā –ĺ–ļ—Ä—É–≥–Ľ–Ķ–Ĺ–ł–Ķ–ľ —É –ļ–ĺ–ľ–į–Ĺ–ī—č Minerr: –†–Ķ—ą–ł—ā—Ć —Ā–ł—Ā—ā–Ķ–ľ—É –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ—č—Ö —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ 4-–ľ—Ź —Ā–Ņ–ĺ—Ā–ĺ–Ī–į–ľ–ł, –≤—č–Ņ–ĺ–Ľ–Ĺ–ł—ā—Ć –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ—É –Ņ–ĺ –ĺ–ī–Ĺ–ĺ–ľ—É –ł–∑ —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 12. –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į 24 –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –≥—Ä–į—Ą–ł–ļ–į –ĺ–ī–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł –ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł –≤ MathCad –ľ–ĺ–∂–Ĺ–ĺ 2-–ľ—Ź —Ā–Ņ–ĺ—Ā–ĺ–Ī–į–ľ–ł. 1. –°–Ņ–ĺ—Ā–ĺ–Ī –Ě—É–∂–Ĺ–ĺ –≤–≤–Ķ—Ā—ā–ł —Ą—É–Ĺ–ļ—Ü–ł—é –ł –Ķ–Ķ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł—Ź, –Ĺ–į –Ņ–į–Ĺ–Ķ–Ľ–ł –ł–Ĺ—Ā—ā—Ä—É–ľ–Ķ–Ĺ—ā–ĺ–≤ –≤—č–Ī—Ä–į—ā—Ć 2-—Ö –ľ–Ķ—Ä–Ĺ—č–Ļ –≥—Ä–į—Ą–ł–ļ –ł –Ņ–ĺ–ī–Ņ–ł—Ā–į—ā—Ć –ĺ—Ā–ł –į–Ī—Ā—Ü–ł—Ā—Ā –ł –ĺ—Ä–ī–ł–Ĺ–į—ā –• –ł F(X) —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 5): –†–ł—Ā—É–Ĺ–ĺ–ļ 5 –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –≥—Ä–į—Ą–ł–ļ–į —Ą—É–Ĺ–ļ—Ü–ł–ł 2. –°–Ņ–ĺ—Ā–ĺ–Ī –Ě—É–∂–Ĺ–ĺ –≤–≤–Ķ—Ā—ā–ł —Ā–į–ľ—É —Ą—É–Ĺ–ļ—Ü–ł—é –≤ –Ņ–ĺ–ī–Ņ–ł—Ā–ł –ĺ—Ā–ł –ĺ—Ä–ī–ł–Ĺ–į—ā. –ě—Ā—Ć –į–Ī—Ā—Ü–ł—Ā—Ā –Ņ–ĺ–ľ–Ķ—ā–ł—ā—Ć —ā–į–ļ –∂–Ķ –• (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 6): –†–ł—Ā—É–Ĺ–ĺ–ļ 6 –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –≥—Ä–į—Ą–ł–ļ–į —Ą—É–Ĺ–ļ—Ü–ł–ł Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 13. –í –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ—č—Ö —Ā–Ņ–ĺ—Ā–ĺ–Ī–į—Ö –ľ—č –≤–≤–ĺ–ī–ł–Ľ–ł –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł–Ķ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –• –Ņ—É—ā–Ķ–ľ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł—Ź –≤–ł–ī–ł–ľ–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā–ł –≥—Ä–į—Ą–ł–ļ–į (–ĺ—ā 0 –ī–ĺ 2ŌÄ). –Ē–Ľ—Ź —ā–ĺ–≥–ĺ, —á—ā–ĺ–Ī—č —Ā–ĺ–∑–ī–į—ā—Ć –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł–Ķ —Ā–į–ľ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ, –Ĺ—É–∂–Ĺ–ĺ –Ĺ–į–ī —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ –∑–į–Ņ–ł—Ā–į—ā—Ć —Ā—ā—Ä–ĺ—á–ļ—É ÔĀįÔÉóÔÄĹ 2..0:X –Ē–≤–Ķ —ā–ĺ—á–ļ–ł –Ņ–ĺ–ī—Ä—Ź–ī –Ĺ—É–∂–Ĺ–ĺ —Ā—ā–į–≤–ł—ā—Ć —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–Ļ –ļ–Ĺ–ĺ–Ņ–ļ–ĺ–Ļ –≤ –Ņ–į–Ĺ–Ķ–Ľ–ł –ú–į—ā—Ä–ł—Ü–į (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 7) –†–ł—Ā—É–Ĺ–ĺ–ļ 7 –ě—Ä–≥–į–Ĺ–ł–∑–į—Ü–ł—Ź –≤–≤–ĺ–ī–į –ī–≤—É—Ö —ā–ĺ—á–Ķ–ļ. –í–ĺ—ā —á—ā–ĺ –≤ —ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –Ņ–ĺ–Ľ—É—á–ł—ā—Ā—Ź (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 8): –†–ł—Ā—É–Ĺ–ĺ–ļ 8 –†–Ķ–∑—É–Ľ—Ć—ā–į—ā—č –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –≥—Ä–į—Ą–ł–ļ–į –Ę–į–ļ–ĺ–Ļ –≤–ł–ī –≥—Ä–į—Ą–ł–ļ–ĺ–≤ –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ľ–Ķ–Ĺ —ā–Ķ–ľ, —á—ā–ĺ MathCad –Ņ–ĺ —É–ľ–ĺ–Ľ—á–į–Ĺ–ł—é –Ī–Ķ—Ä–Ķ—ā —ą–į–≥ —Ä–į–≤–Ĺ—č–ľ –Ķ–ī–ł–Ĺ–ł—Ü–Ķ. –Ē–Ľ—Ź –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —ą–į–≥–į –Ĺ—É–∂–Ĺ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ—Ā—ā–ł –Ĺ–Ķ—Ö–ł—ā—Ä—č–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —Ą–ĺ—Ä–ľ—É–Ľ—č —É—ā–ĺ—á–Ĺ–Ķ–Ĺ–ł—Ź ‚Äď –Ņ–ĺ—Ā–Ľ–Ķ –Ĺ—É–Ľ—Ź –Ņ–ĺ—Ā—ā–į–≤–ł—ā—Ć –∑–į–Ņ—Ź—ā—É—é –ł –≤–≤–Ķ—Ā—ā–ł —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ —á–ł—Ā–Ľ–ĺ —Ā —É—á–Ķ—ā–ĺ–ľ —ą–į–≥–į (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 9): ÔĀįÔÉóÔÄĹ 2..001.0,0:X Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 14. –Ę–ĺ–≥–ī–į –Ņ–ĺ–Ľ—É—á–ł—ā—Ā—Ź —ā–į–ļ: –†–ł—Ā—É–Ĺ–ĺ–ļ 9 –†–Ķ–∑—É–Ľ—Ć—ā–į—ā—č –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –≥—Ä–į—Ą–ł–ļ–į —Ā –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–Ĺ—č–ľ —ą–į–≥–ĺ–ľ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ē—Ā–Ľ–ł –Ī—č –Ĺ–į–ľ –Ī—č–Ľ–ĺ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ņ–ĺ–Ľ—É—á–ł—ā—Ć –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ –ĺ—ā 1–ī–ĺ 2ŌÄ —ā–ĺ –∑–į–Ņ–ł—Ā—Ć –≤—č–≥–Ľ—Ź–ī–Ķ–Ľ–į –Ī—č —ā–į–ļ: ÔĀįÔÉóÔÄĹ 2..001.1,1:X , —ā.–Ķ. –ļ 1 –ľ—č –Ņ—Ä–ł–Ī–į–≤–ł–Ľ–ł —ā–ĺ—ā –∂–Ķ —ą–į–≥ –≤ 0,001 –ł –Ņ–ĺ–Ľ—É—á–ł–Ľ–ł 1,001 –Ě—É–∂–Ĺ–ĺ –ĺ–Ī—Ä–į—ā–ł—ā—Ć –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ, —á—ā–ĺ –≤ MathCad'–Ķ —Ä–į–∑–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —á–ł—Ā–Ľ–į –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ ¬ę,¬Ľ –į ¬ę.¬Ľ –ó–į–ī–į–Ĺ–ł–Ķ: –ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł –ī–≤—É–ľ—Ź —Ā–Ņ–ĺ—Ā–ĺ–Ī–į–ľ–ł –ł –Ņ–ĺ—Ā—ā–į–≤–ł—ā—Ć –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł—Ź –ī–≤—É–ľ—Ź —Ā–Ņ–ĺ—Ā–ĺ–Ī–į–ľ–ł (–≤—Ā–Ķ–≥–ĺ 4 –≥—Ä–į—Ą–ł–ļ–į). 1. )2sin( xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 2. )2cos( xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 3. )2sin( 4 1 xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 4. )sin( 1 x Y ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 5. )tan(xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 6. )2ln( xY ÔÄĹ ÔĀõ ÔĀĚ2...0ÔÉéX Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 15. 7. x e Y 1 ÔÄĹ ÔĀõ ÔĀĚ12...6ÔÉéX 8. x Y 5.0ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 9. )(sin2 xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 10. 2 )sin(xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 11. )(tan2 xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 12. x x Y 2 )ln( ÔÄĹ ÔĀõ ÔĀĚ3.12...6.8ÔÉéX 13. 2 54 xaY ÔÄęÔÄĹ ÔĀõ ÔĀĚ 1.2,3.12...6.8 ÔÄĹÔÉé AX 14. )2sec( xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 15. 3 xY ÔÄĹ ÔĀõ ÔĀĚ12...6ÔÉéX 16. AXctgY ÔÄ≠ÔÄęÔÄĹ ) 4 ( ÔĀį ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 17. AXctgY ÔÄ≠ÔÄęÔÄĹ ) 4 ( ÔĀį ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 18. ÔÄ® ÔÄ©1 1 ÔÄę ÔÄĹ X Y ÔĀõ ÔĀĚ3.12...6.8ÔÉéX 19. 22 AXY ÔÄ≠ÔÄĹ ÔĀõ ÔĀĚ 1.2,3.12...6.8 ÔÄĹÔÉé AX 20. ÔĀõ ÔĀĚ12...6ÔÉéX 21. XAXY ÔÄ≠ÔÄęÔÄĹ )ln( ÔĀõ ÔĀĚ 1.2,3.12...6.8 ÔÄĹÔÉé AX 22. AXctgY ÔÄ≠ÔÄęÔÄĹ ) 4 ( ÔĀį ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 1.2ÔÄĹA 23. AXY ÔÄ≠ÔÄęÔÄĹ ) 4 sin( ÔĀį ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 1.2ÔÄĹA 24. 1ÔÄĹ ÔÄĹ x eY ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 25. x AY 2 sin 1 ÔÄ≠ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX ) 4 (cos ÔĀį ÔÄęÔÄĹ XecY Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 16. 26. xxY ÔÄęÔÄĹ )2ln( ÔĀõ ÔĀĚ2...0ÔÉéX 27. )cos( 1 x e Y x ÔÄęÔÄĹ ÔĀõ ÔĀĚ12...6ÔÉéX Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 17. –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į 25 –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –≥—Ä–į—Ą–ł–ļ–ĺ–≤ —Ä—Ź–ī–į —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ē–Ľ—Ź —ā–ĺ–≥–ĺ, —á—ā–ĺ–Ī—č –Ņ–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –≤ –Ĺ–į –ĺ–ī–Ĺ–ĺ–ľ –≥—Ä–į—Ą–ł–ļ–Ķ –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ —Ą—É–Ĺ–ļ—Ü–ł–Ļ, –Ĺ—É–∂–Ĺ–ĺ –Ņ—Ä–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ĺ—Ā–ł –ĺ—Ä–ī–ł–Ĺ–į—ā –∑–į–ī–į—ā—Ć –ł—Ö —á–Ķ—Ä–Ķ–∑ –∑–į–Ņ—Ź—ā—É—é (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 10): –†–ł—Ā—É–Ĺ–ĺ–ļ 10 –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –≥—Ä–į—Ą–ł–ļ–ĺ–≤ –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ē–Ľ—Ź —ā–ĺ–≥–ĺ, —á—ā–ĺ–Ī—č –ł–∑–ľ–Ķ–Ĺ–ł—ā —ā–ł–Ņ –ł –≤–ł–ī –Ľ–ł–Ĺ–ł–Ļ –Ĺ–į –≥—Ä–į—Ą–ł–ļ–Ķ, –Ĺ—É–∂–Ĺ–ĺ –ī–≤–į–∂–ī—č –ļ–Ľ–ł–ļ–Ĺ—É—ā—Ć –Ľ–Ķ–≤–ĺ–Ļ –ļ–Ĺ–ĺ–Ņ–ļ–ĺ–Ļ –ľ—č—ą–ł –≤ –Ķ–≥–ĺ –ĺ–Ī–Ľ–į—Ā—ā—Ć –ł –≤—č–Ī—Ä–į—ā—Ć –≤–ļ–Ľ–į–ī–ļ—É —ā—Ä–į—Ā—Ā–ł—Ä–ĺ–≤–ļ–į (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 11). –†–ł—Ā—É–Ĺ–ĺ–ļ 11 –ě–ļ–Ĺ–ĺ —Ą–ĺ—Ä–ľ–į—ā–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź –ī–≤—É–ľ–Ķ—Ä–Ĺ—č—Ö –≥—Ä–į—Ą–ł–ļ–ĺ–≤ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 18. –ü–ĺ–ł—Ā–ļ —ā–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –ė–ľ–Ķ–Ķ–ľ 2 —Ą—É–Ĺ–ļ—Ü–ł–ł: y:=x2 y:=8+3‚ąôx –°—ā—Ä–ĺ–ł–ľ –ł—Ö –≥—Ä–į—Ą–ł–ļ–ł –Ĺ–į –ĺ–ī–Ĺ–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā–ł –ė—Č–Ķ–ľ —ā–ĺ—á–ļ—É –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ĺ–į —É—á–į—Ā—ā–ļ–Ķ (-‚ąě;0) –ė—Č–Ķ–ľ —ā–ĺ—á–ļ—É –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ĺ–į —É—á–į—Ā—ā–ļ–Ķ [0;+‚ąě]. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 19. –†–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ 12 –†–ł—Ā—É–Ĺ–ĺ–ļ 12 –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —ā–ĺ—á–Ķ–ļ –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –≥—Ä–į—Ą–ł–ļ–ĺ–≤ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 20. –í–į—Ä–ł–į–Ĺ—ā—č –∑–į–ī–į–Ĺ–ł–Ļ –ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł: 1. ÔÄ® ÔÄ©1ln ÔÄęÔÄĹ XY , )2sin( xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX 2. ]...0[,)2(],2.5...1[,)2( 2 ÔĀįÔÉéÔÄĹÔÉéÔÄęÔÄĹ XXctgYAXA x e Y x 3. ]4...5.2[,]2...0[)cos(,)ln(* 1 2 2 ÔÉéÔÉéÔÄ≠ÔÄĹÔÄĹ AXAxYXx x Y ÔĀį 4. )*5.0tan(6,]10..1[)(*93 XYBXXBXY ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄęÔÄĹ 5. )2cos(],2.5...1[,]5...1[)( 2 5.0 2 XYAXeA x Y x x ÔÄĹÔÉéÔÉéÔÄęÔÄĹ 6. ]4...5.2[,]2...0[) 2 cos(,)2ln(* *2 2 5. ÔÉéÔÉéÔÄęÔÄĹÔÄĹ AXA x Yx x x Y ÔĀį 7. )*5.0(6,]10..1[)(*5.02 3 XctgYBXeBXY x ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄęÔÄĹ 8. 2,]10..1[)ln(*5,]1..5.0[)cos( 2 ÔÄĹÔÉéÔÄęÔÄĹÔÄĹÔÉéÔÄęÔÄĹ AXXxAYAXAeY x 9. A x ctgYAXe x A Y x *2) 2 (3,]15...2[)ln(* *2 2 2 ÔÄęÔÄĹÔÄĹÔÉéÔÄĹ 10. x exYAXAXAY ÔÄęÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ )2sec(5,]4..1[2)*ln( 3 11. x e X YXX X X Y ÔÄęÔÄĹÔÉéÔÄęÔÄĹ ) 4 cos(,]8..2[ )ln( 3 12. 2, )cos( 4,]20...1[*25.0 2 3 ÔÄĹÔÄĹÔÄĹÔÉéÔÄęÔÄĹ A X A YBXBY x 13. 322 5.0)5.0sin(2,]3...5.2[)ln(5*4 ÔÄ≠ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄęÔÄĹ XYAXXXAY 14. ,) 3 cos(],2.5...1[,]5...1[)8.0( 2 23 X YAXA x A Y x ÔÄĹÔÉéÔÉéÔÄęÔÄĹ 15. 2 )ln(*5,]1..5.0[*2)(cos X A X AYAXAeecY x ÔÄęÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ 16. ,)sin()2(],2.5...1[,]5.2...1[))ln(2(* 2 xXtgYAXXA A e Y x ÔÄ≠ÔÄĹÔÉéÔÉéÔÄęÔÄĹ ÔÄ≠ 17. 32 *2) 2 sin(3,]5...2[)ln(* )ln( **2 A x YAXe x AX Y x ÔÄęÔÄĹÔÄĹÔÉéÔÄĹ ÔÄ≠ 18. 2 )*ln(*5,]1..5.0[*2)sin( XxAAYAXAeY x ÔÄęÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ 19. ,) 3 2(],2.5...1[,]5...1[)( 2 X ctgYAXXA x e Y x ÔÄĹÔÉéÔÉéÔÄ≠ÔÄĹ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 21. 20. XXAAYAXAeY x ÔÄ≠ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ ÔÄ≠ )**4ln(*5,]1..5.0[*2)cos( 2 21. ,) 4 cos(],2.5...1[,]5...1[)8.0( *5.0 23 X YAXA X X Y x ÔÄĹÔÉéÔÉéÔÄęÔÄĹ 22. )cos( 4,]20...1[*25.0 2 3 X A YBXBY x ÔÄĹÔÄĹÔÉéÔÄęÔÄĹ 23. 4 )2( 7,]10.0[*5*4 2 Xtg YAX A X AY ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ 24. BxYBX B X eY x *2)2sin(4,]5.2...5.0[ *5.03 ÔÄęÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ 25. ,)3sin(],2.5...1[,]5...1[)*2( 2 8.0 22 XYAXeA x Y x x ÔÄĹÔÉéÔÉéÔÄęÔÄĹ 26. 1.2,) 2 cos(,]5...0[)2ln(* *2 2 5. ÔÄĹÔÄęÔÄĹÔÉéÔÄĹ AA x YXx x x Y 27. ]2...0[,) 3 cos(],2.5...1[,)8.0( 2 23 ÔĀįÔÉéÔÄĹÔÉéÔÄęÔÄĹ X X YAA x A Y x 28. ]2...0[,) 3 cos(],2.5...1[,)8.0( 2 23 ÔĀįÔÉéÔÄĹÔÉéÔÄęÔÄĹ X X YAA x A Y x Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 22. –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į 26 –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –≥—Ä–į—Ą–ł–ļ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ķ–Ļ. –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–ł —Ā–Ņ–ĺ—Ā–ĺ–Ī–į –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –≥—Ä–į—Ą–ł–ļ–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –≤ MathCad'–Ķ. 1. –°–Ņ–ĺ—Ā–ĺ–Ī –Ē–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –∑–į–Ņ–ł—Ā–į—ā—Ć —Ą—É–Ĺ–ļ—Ü–ł—é –≤ MathCad'–Ķ, –≤—č–Ī—Ä–į—ā—Ć –≥—Ä–į—Ą–ł–ļ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ł –≤–≤–Ķ—Ā—ā–ł –Ī—É–ļ–≤—É —Ą—É–Ĺ–ļ—Ü–ł–ł: –í —ć—ā–ĺ–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ķ –≤—Ā–Ķ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—č –Ņ–ĺ–ī–Ī–ł—Ä–į—é—ā—Ā—Ź –į–≤—ā–ĺ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł, –ł –ľ—č –Ĺ–Ķ –ľ–ĺ–∂–Ķ–ľ –ĺ–Ņ–Ķ—Ä–į—ā–ł–≤–Ĺ–ĺ –ł—Ö –ł–∑–ľ–Ķ–Ĺ—Ź—ā—Ć. –í –ł—ā–ĺ–≥–Ķ –ľ—č –≤–ł–ī–ł–ľ —Ą—É–Ĺ–ļ—Ü–ł—é, –Ņ–ĺ–≤—ā–ĺ—Ä–Ķ–Ĺ–Ĺ—É—é –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ —Ä–į–∑. –†–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ 13 –†–ł—Ā—É–Ĺ–ĺ–ļ 13 –†–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –Ņ–Ķ—Ä–≤—č–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ 2. –°–Ņ–ĺ—Ā–ĺ–Ī –£–ļ–į–∑—č–≤–į–Ķ–ľ, —á—ā–ĺ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—č —Ö –ł —É –Ī—É–ī—É—ā –ł–ľ–Ķ—ā—Ć, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, 20 –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –Ī—É–ī—É—ā –ł–∑–ľ–Ķ–Ĺ—Ź—ā—Ć—Ā—Ź –Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ. –ü–ĺ—Ā–Ľ–Ķ —ć—ā–ĺ–≥–ĺ —É–ļ–į–∑—č–≤–į–Ķ–ľ –Ĺ–į—ą—É —Ą—É–Ĺ–ļ—Ü–ł—é –ł –Ņ—Ä–ł—Ä–į–≤–Ĺ–ł–≤–į–Ķ–ľ –Ķ–Ķ –ļ —Ä–Ķ–∑—É–Ľ—Ć—ā–ł—Ä—É—é—Č–Ķ–Ļ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ Z. –í –≥—Ä–į—Ą–ł–ļ–Ķ —ā–į–ļ –∂–Ķ —É–ļ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–į—Ź Z. –Ē–ĺ—Ā—ā–ĺ–ł–Ĺ—Ā—ā–≤–ĺ–ľ –ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–Ņ–ĺ—Ā–ĺ–Ī–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä–ĺ—Ā—ā–ĺ—ā–į –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤, —á—ā–ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –Ľ–Ķ–≥–ļ–ĺ –≤—č–ī–Ķ–Ľ—Ź—ā—Ć –Ĺ–į—ą—É —Ą—É–Ĺ–ļ—Ü–ł—é –ł–∑ –Ņ–ĺ–Ľ—Ź –Ķ—ź –Ņ–ĺ–≤—ā–ĺ—Ä–Ķ–Ĺ–ł–Ļ. –†–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ 14 Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 23. –†–ł—Ā—É–Ĺ–ĺ–ļ 14 –†–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –≤—ā–ĺ—Ä—č–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 24. 3. –°–Ņ–ĺ—Ā–ĺ–Ī —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ —Ą—É–Ĺ–ļ—Ü–ł–ł CreateMesh –ü–ĺ—Ā–Ľ–Ķ –≤–≤–Ķ–ī–Ķ–Ĺ–ł—Ź —Ą—É–Ĺ–ļ—Ü–ł–ł F(x,y), –Ņ—Ä–ł—Ā–≤–į–ł–≤–į–Ķ–ľ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –ö –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ CreateMesh, –ļ–ĺ—ā–ĺ—Ä–į—Ź –ł–ľ–Ķ–Ķ—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—č: –°reateMesh(F, x0, x1, y0, y1, xgrid, ygrid, fmap) - —Ā–ĺ–∑–ī–į–Ĺ–ł–Ķ –≤–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –ľ–į—Ā—Ā–ł–≤–į, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—Č–Ķ–≥–ĺ —Ö-, —É- –ł z-–ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł, –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ F; F(x,y) ‚ÄĒ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź –ł–∑ —ā—Ä–Ķ—Ö —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤, –∑–į–ī–į–Ĺ–Ĺ–į—Ź –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ī–≤—É—Ö –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–ĺ–≤ x –ł y; x0, y0 ‚ÄĒ –Ĺ–ł–∂–Ĺ–ł–Ķ –Ņ—Ä–Ķ–ī–Ķ–Ľ—č –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–ĺ–≤ x, y (–Ņ–ĺ —É–ľ–ĺ–Ľ—á–į–Ĺ–ł—é -5); x1, y1 ‚ÄĒ –≤–Ķ—Ä—Ö–Ĺ–ł–Ķ –Ņ—Ä–Ķ–ī–Ķ–Ľ—č –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–ĺ–≤ x, y (–Ņ–ĺ —É–ľ–ĺ–Ľ—á–į–Ĺ–ł—é 5); xgrid, ygrid ‚ÄĒ —á–ł—Ā–Ľ–ĺ —ā–ĺ—á–Ķ–ļ —Ā–Ķ—ā–ļ–ł –Ņ–ĺ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–ľ x –ł y (–Ņ–ĺ —É–ľ–ĺ–Ľ—á–į–Ĺ–ł—é 20); fmap ‚ÄĒ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź –ł–∑ —ā—Ä–Ķ—Ö —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤ –ĺ—ā —ā—Ä–Ķ—Ö –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–ĺ–≤, –∑–į–ī–į—é—Č–į—Ź –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā. –ė–∑–ľ–Ķ–Ĺ—Ź—Ź –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—č —Ą—É–Ĺ–ļ—Ü–ł–ł CreateMesh –ľ–ĺ–∂–Ĺ–ĺ —ā–į–ļ–∂–Ķ –Ľ–Ķ–≥–ļ–ĺ –≤—č–ī–Ķ–Ľ–ł—ā—Ć –ł—Ā–ļ–ĺ–ľ—É—é —Ą—É–Ĺ–ļ—Ü–ł—é –ł–∑ –Ņ–ĺ–Ľ—Ź –Ķ–Ķ –Ņ–ĺ–≤—ā–ĺ—Ä–Ķ–Ĺ–ł–Ļ. –†–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ 15 –†–ł—Ā—É–Ĺ–ĺ–ļ 14 –†–Ķ–∑—É–Ľ—Ć—ā–į—ā –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł —Ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ–ľ —Ą—É–Ĺ–ļ—Ü–ł–ł CreateMesh Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 25. –Ē–Ľ—Ź –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā—Ć –ľ–ĺ–∂–Ĺ–ĺ –∑–į–Ľ–ł—ā—Ć —Ü–≤–Ķ—ā–ĺ–ľ. –Ē–Ľ—Ź —ć—ā–ĺ–≥–ĺ –Ĺ—É–∂–Ĺ–ĺ –ī–≤–į–∂–ī—č –ļ–Ľ–ł–ļ–Ĺ—É—ā—Ć –Ľ–Ķ–≤–ĺ–Ļ –ļ–Ĺ–ĺ–Ņ–ļ–ĺ–Ļ –ľ—č—ą–ł –Ĺ–į –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł –ł –≤–ĺ –≤–ļ–Ľ–į–ī–ļ–Ķ –ĺ—Ą–ĺ—Ä–ľ–Ľ–Ķ–Ĺ–ł–Ķ –≤—č–Ī—Ä–į—ā—Ć –Ņ—É–Ĺ–ļ—ā—č (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 16) –ü–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā—Ć —Ā –∑–į–Ľ–ł–≤–ļ–ĺ–Ļ –ł –ö–į—Ä—ā–į —Ü–≤–Ķ—ā–ĺ–≤ –†–ł—Ā—É–Ĺ–ĺ–ļ 16 –ė—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ –∑–į–Ľ–ł–≤–ļ–ł —Ü–≤–Ķ—ā–ĺ–ľ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 26. –í–į—Ä–ł–į–Ĺ—ā—č –∑–į–ī–į–Ĺ–ł–Ļ –ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –ĺ–Ī—ä–Ķ–ľ–Ĺ—č–Ķ –≥—Ä–į—Ą–ł–ļ–ł –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ķ–Ļ: 1. )sin(),( 44 YXyxf ÔÄęÔÄĹ 2. )(),( 44 YXtgyxf ÔÄęÔÄĹ 3. )sin()cos(),( 244 XYXyxf ÔÄ≠ÔÄęÔÄĹ 4. )*5.0cos(),( 44 YXyxf ÔÄęÔÄĹ 5. )sin()sin(),( 244 XYXyxf ÔÄęÔÄęÔÄĹ 6. )sin()cos(),( 244 XYXyxf ÔÄ≠ÔÄęÔÄĹ 7. )sin()sin(),( 22 XYyxf ÔÄęÔÄĹ 8. )()*5.0(),( 22 XtgYtgyxf ÔÄęÔÄĹ 9. )*sin(),( 4 YXyxf ÔÄĹ 10. )*5.0*(),( 4 YXtgyxf ÔÄĹ 11. )*sin()cos(),( 444 YXYXyxf ÔÄęÔÄęÔÄĹ 12. )*sin(),( 4 YXyxf ÔÄĹ 13. ) 3 2 sin()sin(),( 22 XYyxf ÔÄ≠ÔÄĹ 14. )sin()cos(),( 244 XYXyxf ÔÄ≠ÔÄęÔÄĹ 15. )()(),( 22 XtgYtgyxf ÔÄęÔÄĹ 16. )**5.0cos(),( YXyxf ÔÄĹ 17. )*sin()cos(),( 444 YXYXyxf ÔÄęÔÄęÔÄĹ 18. )*sin(),( 22 YXyxf ÔÄĹ 19. )*5.0*5.0(),( 22 YXtgyxf ÔÄ≠ÔÄĹ 20. )(),( 22 YXctgyxf ÔÄęÔÄĹ 21. )*5.0cos(),( 44 YXyxf ÔÄęÔÄĹ 22. )sec(),( 24 YXyxf ÔÄęÔÄĹ 23. )**5.0sin(),( 44 YXyxf ÔÄĹ 24. )cos()sin(),( 2244 YXYXyxf ÔÄ≠ÔÄęÔÄęÔÄĹ 25. )*5.0*(),( 4 YXtgyxf ÔÄĹ 26. )sin(),( 44 YXyxf ÔÄęÔÄĹ 27. )sin()(),( 3322 YXYXtgyxf ÔÄęÔÄ≠ÔÄęÔÄĹ 28. )*5.0cos(),( 44 YXyxf ÔÄęÔÄĹ 29. )*cos(),( 33 YXyxf ÔÄĹ 30. )cos()sin(),( 44 XYyxf ÔÄęÔÄĹ 31. )*5.0*(),( 4 YXtgyxf ÔÄĹ 32. )5.0()*5.0(),( 22 XctgYctgyxf ÔÄęÔÄĹ 33. )*sin()cos(),( 444 YXYXyxf ÔÄęÔÄęÔÄĹ 34. )*5.0*(),( 4 YXtgyxf ÔÄĹ 35. )*5.0cos(),( 44 YXyxf ÔÄęÔÄĹ 36. ) 3 2 cos()cos(),( 22 XYyxf ÔÄ≠ÔÄĹ 37. )sin()cos(),( 244 XYXyxf ÔÄ≠ÔÄęÔÄĹ 38. )()(),( 22 XtgYtgyxf ÔÄęÔÄĹ 39. )sin(),( 44 YXyxf ÔÄęÔÄĹ 40. )sin()sin(),( 22 XYyxf ÔÄęÔÄĹ 41. )*sin()cos(),( 444 YXYXyxf ÔÄęÔÄęÔÄĹ 42. )*5.0cos(),( 44 YXyxf ÔÄęÔÄĹ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 27. –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į 27. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ –ĺ–Ņ–Ķ—Ä–į—ā–ĺ—Ä —Ā—É–ľ–ľ—č, –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ, –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č—Ö –ł –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ–ĺ–≤ –Ē–Ľ—Ź –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź —Ā—É–ľ–ľ—č, –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ, –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č—Ö –ł –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ–ĺ–≤ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –≤–≤–Ķ—Ā—ā–ł —Ą—É–Ĺ–ļ—Ü–ł—é –ł —ā—Ä–Ķ–Ī—É–Ķ–ľ—č–Ļ –ĺ–Ņ–Ķ—Ä–į—ā–ĺ—Ä –≤ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–ł —Ā —É—Ā–Ľ–ĺ–≤–ł—Ź–ľ–ł –∑–į–ī–į–Ĺ–ł—Ź: –ö–į–ļ –≤–ł–ī–Ĺ–ĺ –ł–∑ –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ—č—Ö –Ņ—É–Ĺ–ļ—ā–ĺ–≤, —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā—č –ľ–ĺ–∂–Ĺ–ĺ –≤—č—á–ł—Ā–Ľ–ł—ā—Ć –≤ –ĺ–Ī—Č–Ķ–ľ –ł–Ľ–ł —á–ł—Ā–Ľ–ĺ–≤–ĺ–ľ –≤–ł–ī–Ķ. –ó–į–ī–į–Ĺ–ł–Ķ. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—ā–ĺ—Ä —Ā—É–ľ–ľ—č, –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ, –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č—Ö –ł –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ–ĺ–≤: –ó–į–ī–į–Ĺ–ł–Ķ 1. –ü–ĺ–ī—Ā—á–ł—ā–į—ā—Ć —Ā—É–ľ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—č—Ö –≤ –ĺ–Ī–Ķ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł—Ź—Ö –Ľ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–ĺ–Ļ —Ä–į–Ī–ĺ—ā–Ķ 25. –ó–į–ī–į–Ĺ–ł–Ķ 2. –ü–ĺ–ī—Ā—á–ł—ā–į—ā—Ć –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ļ –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—č—Ö –≤ –ĺ–Ī–Ķ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł—Ź—Ö –Ľ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–ĺ–Ļ —Ä–į–Ī–ĺ—ā–Ķ 25. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 28. –ó–į–ī–į–Ĺ–ł–Ķ 3. –í—č—á–ł—Ā–Ľ–ł—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č—Ö —Ā–Ľ–Ķ–ī—É—é—Č–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ (–Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–į—Ź –•): )(sin2 xY ÔÄĹ )2( XtgY ÔÄĹ )(cos2 xY ÔÄĹ )*3(sin2 xY ÔÄĹ )ln(*8 xY ÔÄĹ )ln(x x Y ÔÄĹ )ln(x e Y x ÔÄĹ x x Y )sin( ÔÄĹ x Y 5.0ÔÄĹ 2 *5*4 XAY ÔÄ≠ÔÄĹ 2 )ln(*2 xxY ÔÄ≠ÔÄĹ 5.0 *6 x x Y ÔÄĹ )sin( 2 xY ÔÄĹ ) 2 (sin2 x Y ÔÄĹ x eY ÔÄĹ )ln( 1 x Y ÔÄĹ 22 *5*4 XAY ÔÄęÔÄĹ 3 xY ÔÄĹ )2( XctgY ÔÄĹ x e Y 2 ÔÄĹ )ln(*2 2 xY ÔÄĹ A x Y ÔÄĹ ) 1 (sin2 x Y ÔÄĹ )*3(cos 22 xY ÔÄĹ )ln(*8.0 xY x ÔÄĹ 2 *5*4 XAY ÔÄ≠ÔÄĹ )ln(x x Y ÔÄĹ )(sin2 xY ÔÄĹ –ó–į–ī–į–Ĺ–ł–Ķ 4. –í—č—á–ł—Ā–Ľ–ł—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ–ĺ–≤ —Ā–Ľ–Ķ–ī—É—é—Č–ł—Ö –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ļ: 1. )ln(*8 xY ÔÄĹ 2. )(sin2 xY ÔÄĹ 3. )ln(x x Y ÔÄĹ 4. 2 *5*4 XAY ÔÄ≠ÔÄĹ 5. x e Y 2 ÔÄĹ 6. ) 1 (sin2 x Y ÔÄĹ 7. )*3(sin2 xY ÔÄĹ 8. A x Y ÔÄĹ 9. x e Y 1 ÔÄĹ 10. )2( XctgY ÔÄĹ 11. )ln(x e Y x ÔÄĹ 12. x Y 5.0ÔÄĹ 13. x x Y )sin( ÔÄĹ 14. )2( xtgY ÔÄĹ 15. ) 2 (sin2 x Y ÔÄĹ 16. )ln(*8.0 xY x ÔÄĹ 17. x eY 2 ÔÄĹ 18. 2 *5.0 xY x ÔÄĹ 19. 22 *5*3 XAY ÔÄ≠ÔÄĹ 20. ) 4 (sin 2 2 x Y ÔÄĹ 21. )ln( 5.0 x Y x ÔÄĹ 22. )22(sin2 ÔÄęÔÄĹ xY 23. )cos(x e Y x ÔÄĹ 24. )2(*8 xctgY ÔÄĹ 25. )ln(*3.0 xY x ÔÄĹ 26. x e Y 1 ÔÄĹ 27. )*3(sin2 xY ÔÄĹ 28. )2( xtgY ÔÄĹ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
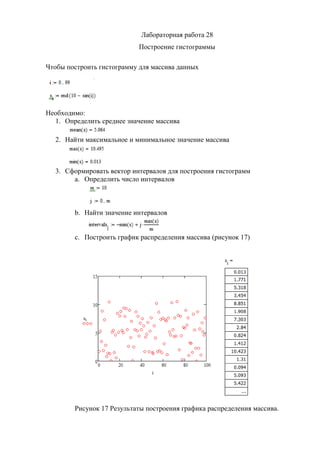
- 29. –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į 28 –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –≥–ł—Ā—ā–ĺ–≥—Ä–į–ľ–ľ—č –ß—ā–ĺ–Ī—č –Ņ–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –≥–ł—Ā—ā–ĺ–≥—Ä–į–ľ–ľ—É –ī–Ľ—Ź –ľ–į—Ā—Ā–ł–≤–į –ī–į–Ĺ–Ĺ—č—Ö –Ě–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ: 1. –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ľ–į—Ā—Ā–ł–≤–į 2. –Ě–į–Ļ—ā–ł –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ –ł –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ľ–į—Ā—Ā–ł–≤–į 3. –°—Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į—ā—Ć –≤–Ķ–ļ—ā–ĺ—Ä –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ĺ–≤ –ī–Ľ—Ź –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –≥–ł—Ā—ā–ĺ–≥—Ä–į–ľ–ľ a. –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć —á–ł—Ā–Ľ–ĺ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ĺ–≤ b. –Ě–į–Ļ—ā–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ĺ–≤ c. –ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –≥—Ä–į—Ą–ł–ļ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –ľ–į—Ā—Ā–ł–≤–į (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 17) –†–ł—Ā—É–Ĺ–ĺ–ļ 17 –†–Ķ–∑—É–Ľ—Ć—ā–į—ā—č –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –≥—Ä–į—Ą–ł–ļ–į —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –ľ–į—Ā—Ā–ł–≤–į. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 30. –Ē–Ľ—Ź —ā–ĺ–≥–ĺ, —á—ā–ĺ–Ī—č –Ņ–ĺ–Ľ—É—á–ł—ā—Ć —ā–ĺ—á–ļ–ł, —Ā–Ľ–Ķ–ī—É–Ķ—ā –≤—č–Ī—Ä–į—ā—Ć —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ķ –Ņ—É–Ĺ–ļ—ā—č –≤ –Ĺ–į—Ā—ā—Ä–ĺ–Ļ–ļ–į—Ö –≥—Ä–į—Ą–ł–ļ–į (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 18): –†–ł—Ā—É–Ĺ–ĺ–ļ 18 –Ě–į—Ā—ā—Ä–ĺ–Ļ–ļ–į –≥—Ä–į—Ą–ł–ļ–į 4. –ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –≥–ł—Ā—ā–ĺ–≥—Ä–į–ľ–ľ—É (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 19) –†–ł—Ā—É–Ĺ–ĺ–ļ 19 –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –≥–ł—Ā—ā–ĺ–≥—Ä–į–ľ–ľ—č –ė–∑ –≥–ł—Ā—ā–ĺ–≥—Ä–į–ľ–ľ—č –≤–ł–ī–Ĺ–ĺ, —á—ā–ĺ –ī–į–Ĺ–Ĺ—č–Ķ –ľ–į—Ā—Ā–ł–≤–į —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ—č –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ. –Ē–Ľ—Ź —ā–į–ļ–ĺ–≥–ĺ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –≤ –Ĺ–į—Ā—ā—Ä–ĺ–Ļ–ļ–į—Ö –≥—Ä–į—Ą–ł–ļ–į –≤—č–Ī—Ä–į—ā—Ć —ć—ā–ĺ—ā –Ņ—É–Ĺ–ļ—ā (—Ä–ł—Ā—É–Ĺ–ĺ–ļ 20): Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 31. –†–ł—Ā—É–Ĺ–ĺ–ļ 20 –Ě–į—Ā—ā—Ä–ĺ–Ļ–ļ–į –≥–ł—Ā—ā–ĺ–≥—Ä–į–ľ–ľ—č Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 32. –í–į—Ä–ł–į–Ĺ—ā—č –∑–į–ī–į–Ĺ–ł–Ļ 1. )2sin(5 xY ÔÄ≠ÔÄĹ 2. )2cos(3 xY ÔÄ≠ÔÄĹ 3. )2sin( 4 1 7 xY ÔÄ≠ÔÄĹ 4. )sin( 1 4 x Y ÔÄ≠ÔÄĹ 5. )tan(5 xY ÔÄęÔÄĹ 6. )2tan(3 xY ÔÄęÔÄĹ 7. 2 )2sin(13 xY ÔÄ≠ÔÄĹ 8. 2 )sin(12 xY ÔÄ≠ÔÄĹ 9. 2 )tan(8 xY ÔÄęÔÄĹ 10. 2 )2tan(73 xY ÔÄęÔÄĹ 11. )2sec(3 xY ÔÄęÔÄĹ 12. )2(25 xctgY ÔÄęÔÄĹ 13. )2(15 xctgY ÔÄęÔÄĹ 14. )(5 xctgY ÔÄęÔÄĹ 15. 2 )2(2 xctgY ÔÄęÔÄĹ 16. )2cos(5,04 xY ÔÄ≠ÔÄĹ 17. )2cos(3,018 xY ÔÄ≠ÔÄĹ 18. )2cos(44,03 xY ÔÄ≠ÔÄĹ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 33. –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į 29. 1. –Ē–Ľ—Ź –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–į g(x) –≤—č–Ņ–ĺ–Ľ–Ĺ–ł—ā—Ć —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź: 1) —Ä–į–∑–Ľ–ĺ–∂–ł—ā—Ć –Ĺ–į –ľ–Ĺ–ĺ–∂–ł—ā–Ķ–Ľ–ł, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—é –°–ł–ľ–≤–ĺ–Ľ—Ć–Ĺ—č–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł ÔÉě –§–į–ļ—ā–ĺ—Ä–ł–∑–ĺ–≤–į—ā—Ć; 2) –Ņ–ĺ–ī—Ā—ā–į–≤—Ć—ā–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ x = y + z –≤ g(x), –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—é –°–ł–ľ–≤–ĺ–Ľ—Ć–Ĺ—č–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł ÔÉě –ü–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ķ ÔÉě –ü–ĺ–ī—Ā—ā–į–≤–ł—ā—Ć (–Ņ—Ä–Ķ–ī–≤–į—Ä–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ā–ļ–ĺ–Ņ–ł—Ä–ĺ–≤–į–≤ –Ņ–ĺ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ–ľ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –≤ –Ī—É—Ą–Ķ—Ä –ĺ–Ī–ľ–Ķ–Ĺ–į, –≤—č–ī–Ķ–Ľ–ł–≤ –Ķ–≥–ĺ –ł –Ĺ–į–∂–į–≤ –ļ–ĺ–ľ–Ī–ł–Ĺ–į—Ü–ł—é –ļ–Ľ–į–≤–ł—ą Ctrl + C); 3) –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—é –°–ł–ľ–≤–ĺ–Ľ—Ć–Ĺ—č–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł ÔÉě –†–į–∑–≤–Ķ—Ä–Ĺ—É—ā—Ć, —Ä–į–∑–Ľ–ĺ–∂–ł—ā–Ķ –Ņ–ĺ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ź–ľ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ķ –≤ 2); 4) –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—é –°–ł–ľ–≤–ĺ–Ľ—Ć–Ĺ—č–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł ÔÉě –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–į—Ź ÔÉě –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į—ā—Ć –ļ –ī—Ä–ĺ–Ī–Ĺ–ĺ-—Ä–į—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ–ľ—É –≤–ł–ī—É, —Ā–≤–Ķ—Ä–Ĺ–ł—ā–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ķ –≤ 3), –Ņ–ĺ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ z. –Ę–į–Ī–Ľ–ł—Ü–į 1 –í–į—Ä–ł–į–Ĺ—ā—č –∑–į–ī–į–Ĺ–ł–Ļ ‚ĄĖ –≤–į—Ä–ł–į–Ĺ—ā–į g(x) ‚ĄĖ –≤–į—Ä–ł–į–Ĺ—ā–į g(x) 1 x4 - 2x3 + x2 - 12x + 20 9 x4 + x3 - 17x2 - 45x - 100 2 x4 + 6x3 + x2 - 4x - 60 10 x4 - 5x3 + x2 - 15x + 50 3 x4 - 14x2 - 40x - 75 11 x4 - 4x3 - 2x2 - 20x + 25 4 x4 - x3 + x2 - 11x + 10 12 x4 + 5x3 + 7x2 + 7x - 20 5 x4 - x3 - 29x2 - 71x -140 13 x4 - 7x3 + 7x2 - 5x + 100 6 x4 + 7x3 + 9x2 + 13x - 30 14 x4 + 10x3 +36x2 +70x+ 75 7 x4 + 3x3 - 23x2 - 55x - 150 15 x4 + 9x3 + 31x2 + 59x+ 60 8 x4 - 6x3 + 4x2 + 10x + 75 2. –í—č—á–ł—Ā–Ľ–ł—ā–Ķ –Ņ—Ä–Ķ–ī–Ķ–Ľ—č: 1) 2) 3) 4) 5) 0x 1 xÔÄę( ) 1 x lim ÔÄęÔāģ Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 34. 3. –†–į–∑–Ľ–ĺ–∂–ł—ā–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ĺ–į —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č–Ķ –ī—Ä–ĺ–Ī–ł –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—é –°–ł–ľ–≤–ĺ–Ľ—Ć–Ĺ—č–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł ÔÉě –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–į—Ź ÔÉě –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į—ā—Ć –ļ –ī—Ä–ĺ–Ī–Ĺ–ĺ- —Ä–į—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ–ľ—É –≤–ł–ī—É: 1) xx xx ÔÄ≠ ÔÄęÔÄ≠ 3 2 16 ; 2) ÔÄ® ÔÄ©ÔÄ® ÔÄ©11 23 2 2 ÔÄęÔÄęÔÄę ÔÄ≠ xxx x ; 3) ÔÄ® ÔÄ©3 1 1 ÔÄ≠ ÔÄę xx x ; 4) ÔÄ® ÔÄ© ÔÄ® ÔÄ©31 1645 22 2 ÔÄ≠ÔÄęÔÄ≠ ÔÄęÔÄ≠ xxx xx . Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 35. –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į 30 –£–Ņ—Ä–į–∂–Ĺ–Ķ–Ĺ–ł–Ķ 1. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—é –°–ł–ľ–≤–ĺ–Ľ—č ÔÉě –†–į—Ā—á–Ķ—ā—č ÔÉě –° –Ņ–Ľ–į–≤–į—é—Č–Ķ–Ļ –∑–į–Ņ—Ź—ā–ĺ–Ļ‚Ķ, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ć—ā–Ķ: 1. —á–ł—Ā–Ľ–ĺ ÔĀį –≤ 7 –Ņ–ĺ–∑–ł—Ü–ł—Ź—Ö; 2. —á–ł—Ā–Ľ–ĺ 12,345667 –≤ 3 –Ņ–ĺ–∑–ł—Ü–ł—Ź—Ö. –£–Ņ—Ä–į–∂–Ĺ–Ķ–Ĺ–ł–Ķ 2. –í—č–≤–Ķ–ī–ł—ā–Ķ —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ —á–ł—Ā–Ľ–į –≤ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ļ —Ą–ĺ—Ä–ľ–Ķ, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—é –†–į—Ā—á–Ķ—ā—č ÔÉě –ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č–Ķ –ľ–Ķ–Ĺ—é –°–ł–ľ–≤–ĺ–Ľ—č: 1. 7ÔÄ≠ ; 2. tg (a 3ÔÄ≠ ); 3. i e 4 1 ÔĀį ÔÄę ; –ī–Ľ—Ź –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź 3 –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –≤—č–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –†–į—Ā—á–Ķ—ā—č ÔÉě –ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č–Ķ –ł –£–Ņ—Ä–ĺ—Ā—ā–ł—ā—Ć –ľ–Ķ–Ĺ—é –°–ł–ľ–≤–ĺ–Ľ—č. –£–Ņ—Ä–į–∂–Ĺ–Ķ–Ĺ–ł–Ķ 3. –†–į–∑–Ľ–ĺ–∂–ł—ā–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –≤ —Ä—Ź–ī —Ā –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ļ —ā–ĺ—á–Ĺ–ĺ—Ā—ā—Ć—é, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—é –°–ł–ľ–≤–ĺ–Ľ—č ÔÉě –ü–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ķ ÔÉě –†–į–∑–Ľ–ĺ–∂–ł—ā—Ć –Ĺ–į —Ā–ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–ł–Ķ: 1. ln ( 1 + x), —Ö0 = 0, –Ņ–ĺ—Ä—Ź–ī–ĺ–ļ —Ä–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź 6; 2. sin (x)2 , —Ö0 = 0, –Ņ–ĺ—Ä—Ź–ī–ĺ–ļ —Ä–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź 6. –£–Ņ—Ä–į–∂–Ĺ–Ķ–Ĺ–ł–Ķ 4. –Ě–į–Ļ—ā–ł –Ņ–Ķ—Ä–≤–ĺ–ĺ–Ī—Ä–į–∑–Ĺ—É—é –į–Ĺ–į–Ľ–ł—ā–ł—á–Ķ—Ā–ļ–ł –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł f(x) –ł–∑ —ā–į–Ī–Ľ–ł—Ü—č, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ĺ–Ņ–Ķ—Ä–į—Ü–ł—é –°–ł–ľ–≤–ĺ–Ľ—č ÔÉě –ü–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ķ ÔÉě –ė–Ĺ—ā–Ķ–≥—Ä–į—Ü–ł—Ź. –£–Ņ—Ä–į–∂–Ĺ–Ķ–Ĺ–ł–Ķ 5. –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć —Ā–ł–ľ–≤–ĺ–Ľ—Ć–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ņ–Ķ—Ä–≤–ĺ–Ļ –ł –≤—ā–ĺ—Ä–ĺ–Ļ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č—Ö f(x) –ł–∑ —ā–į–Ī–Ľ–ł—Ü—č, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –ļ–ĺ–ľ–į–Ĺ–ī—É –°–ł–ľ–≤–ĺ–Ľ—č ÔÉě –ü–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ķ ÔÉě –Ē–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—č. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 36. –Ę–į–Ī–Ľ–ł—Ü–į 2 –í–į—Ä–ł–į–Ĺ—ā—č –∑–į–ī–į–Ĺ–ł–Ļ ‚ĄĖ –≤–į—Ä–ł–į–Ĺ—ā–į f(—Ö) ‚ĄĖ –≤–į—Ä–ł–į–Ĺ—ā–į f(—Ö) ‚ĄĖ –≤–į—Ä–ł–į–Ĺ—ā–į f(—Ö) 1 ÔÄ® ÔÄ©12tg1 ÔÄęx 6 x2 ÔÉó ÔÄ® ÔÄ©3arctg x 11 (2x + 3) sin x 2 ÔÄ® ÔÄ©52cos ÔÄęxx 7 xe x 3sin2 12 )3cos1(3cos xx ÔÄ≠ 2 3 1/(x 43 ÔÄęx ) 8 )2(sin2ctg xx 2 13 1/(1 + x + x2 ) 4 ÔÄ® ÔÄ©xx sin1sin ÔÄę 9 (x + 1) sin x 14 ÔÄ® ÔÄ© ÔÄ® ÔÄ©xx ÔÄęÔÄę 21 5 x2 ÔÉó )2lg( ÔÄęx 10 5x + x lg x 15 1ÔÄę ÔÄ≠e x –£–Ņ—Ä–į–∂–Ĺ–Ķ–Ĺ–ł–Ķ 6. 1) –Ę—Ä–į–Ĺ—Ā–Ņ–ĺ–Ĺ–ł—Ä—É–Ļ—ā–Ķ –ľ–į—ā—Ä–ł—Ü—É –ú 1 x x 2 a 2 3 b c d ÔɶÔÉß ÔÉß ÔÉß ÔÉ® ÔÉ∂ÔÉ∑ ÔÉ∑ ÔÉ∑ ÔÉł —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –°–ł–ľ–≤–ĺ–Ľ—č ÔÉě –ú–į—ā—Ä–ł—Ü—č ÔÉě –Ę—Ä–į–Ĺ—Ā–Ņ–ĺ–Ĺ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ. 2) –ė–Ĺ–≤–Ķ—Ä—ā–ł—Ä—É–Ļ—ā–Ķ –ľ–į—ā—Ä–ł—Ü—É 1 x y 2 Ôɶ ÔÉß ÔÉ® ÔÉ∂ ÔÉ∑ ÔÉł —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –°–ł–ľ–≤–ĺ–Ľ—č ÔÉě –ú–į—ā—Ä–ł—Ü—č ÔÉě –ė–Ĺ–≤–Ķ—Ä—ā–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ. 3) –í—č—á–ł—Ā–Ľ–ł—ā–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ć –ľ–į—ā—Ä–ł—Ü—č –ú 1 x x 2 a 2 3 b c d ÔɶÔÉß ÔÉß ÔÉß ÔÉ® ÔÉ∂ÔÉ∑ ÔÉ∑ ÔÉ∑ ÔÉł —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł –°–ł–ľ–≤–ĺ–Ľ—č ÔÉě –ú–į—ā—Ä–ł—Ü—č ÔÉě –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ć. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 37. –°–ü–ė–°–ě–ö –õ–ė–Ę–ē–†–ź–Ę–£–†–ę 1. –ö–ł—Ä—Ć—Ź–Ĺ–ĺ–≤ –Ē.–í. Mathcad 15/Mathcad Prime 1.0. [–Ę–Ķ–ļ—Ā—ā]: –Ď–í–•-–ü–Ķ—ā–Ķ—Ä–Ī—É—Ä–≥, 2012. -428 —Ā. 1. –Ē—Ć—Ź–ļ–ĺ–Ĺ–ĺ–≤ –í.–ü. Mathcad 11/12/13 –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ: –°–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ. [–Ę–Ķ–ļ—Ā—ā]: –ď–ĺ—Ä—Ź—á–į—Ź –Ľ–ł–Ĺ–ł—Ź-–Ę–Ķ–Ľ–Ķ–ļ–ĺ–ľ, 2007, 960 —Ā. Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ
- 38. –ě–ď–õ–ź–í–õ–ē–Ě–ė–ē –í–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ. 3 –°—ā—Ä—É–ļ—ā—É—Ä–į —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ –ĺ–ļ–Ĺ–į Mathcad ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ.. 4 –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į ‚ĄĖ 23 ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ. 6 –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į ‚ĄĖ 24‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ. 12 –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į ‚ĄĖ 25 ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ. 16 –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į ‚ĄĖ 26‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ. 21 –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į ‚ĄĖ 27 ‚Ķ..‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ. 27 –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į ‚ĄĖ 28 .‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ. 29 –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į ‚ĄĖ 29 ‚Ķ.‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ. 33 –õ–į–Ī–ĺ—Ä–į—ā–ĺ—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į ‚ĄĖ 30‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ. 35 –°–ü–ė–°–ě–ö –õ–ė–Ę–ē–†–ź–Ę–£–†–ę ‚Ä¶‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ‚Ķ 37 Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ

















![–ü–ĺ–ł—Ā–ļ —ā–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź
–ė–ľ–Ķ–Ķ–ľ 2 —Ą—É–Ĺ–ļ—Ü–ł–ł:
y:=x2
y:=8+3‚ąôx
–°—ā—Ä–ĺ–ł–ľ –ł—Ö –≥—Ä–į—Ą–ł–ļ–ł –Ĺ–į –ĺ–ī–Ĺ–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā–ł
–ė—Č–Ķ–ľ —ā–ĺ—á–ļ—É –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ĺ–į —É—á–į—Ā—ā–ļ–Ķ (-‚ąě;0)
–ė—Č–Ķ–ľ —ā–ĺ—á–ļ—É –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ĺ–į —É—á–į—Ā—ā–ļ–Ķ [0;+‚ąě].
Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ](https://image.slidesharecdn.com/ocmjlvwgt1mcq1p2kvvn-signature-4a922e7935a85b02b0b80c5cfa82925cda48c81fe0e83a068d0a9d0ef03c7eba-poli-150523202516-lva1-app6891/85/429-2-mathcad-18-320.jpg)

![–í–į—Ä–ł–į–Ĺ—ā—č –∑–į–ī–į–Ĺ–ł–Ļ
–ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –≥—Ä–į—Ą–ł–ļ —Ą—É–Ĺ–ļ—Ü–ł–ł:
1. ÔÄ® ÔÄ©1ln ÔÄęÔÄĹ XY , )2sin( xY ÔÄĹ ÔĀõ ÔĀĚÔĀį2...0ÔÉéX
2. ]...0[,)2(],2.5...1[,)2(
2
ÔĀįÔÉéÔÄĹÔÉéÔÄęÔÄĹ XXctgYAXA
x
e
Y
x
3. ]4...5.2[,]2...0[)cos(,)ln(*
1 2
2
ÔÉéÔÉéÔÄ≠ÔÄĹÔÄĹ AXAxYXx
x
Y ÔĀį
4. )*5.0tan(6,]10..1[)(*93
XYBXXBXY ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄęÔÄĹ
5. )2cos(],2.5...1[,]5...1[)(
2
5.0 2
XYAXeA
x
Y x
x
ÔÄĹÔÉéÔÉéÔÄęÔÄĹ
6. ]4...5.2[,]2...0[)
2
cos(,)2ln(*
*2
2
5.
ÔÉéÔÉéÔÄęÔÄĹÔÄĹ AXA
x
Yx
x
x
Y ÔĀį
7. )*5.0(6,]10..1[)(*5.02 3
XctgYBXeBXY x
ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄęÔÄĹ
8. 2,]10..1[)ln(*5,]1..5.0[)cos( 2
ÔÄĹÔÉéÔÄęÔÄĹÔÄĹÔÉéÔÄęÔÄĹ AXXxAYAXAeY x
9. A
x
ctgYAXe
x
A
Y x
*2)
2
(3,]15...2[)ln(*
*2 2
2
ÔÄęÔÄĹÔÄĹÔÉéÔÄĹ
10. x
exYAXAXAY ÔÄęÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ )2sec(5,]4..1[2)*ln( 3
11. x
e
X
YXX
X
X
Y ÔÄęÔÄĹÔÉéÔÄęÔÄĹ )
4
cos(,]8..2[
)ln(
3
12. 2,
)cos(
4,]20...1[*25.0
2
3
ÔÄĹÔÄĹÔÄĹÔÉéÔÄęÔÄĹ A
X
A
YBXBY x
13. 322
5.0)5.0sin(2,]3...5.2[)ln(5*4 ÔÄ≠ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄęÔÄĹ XYAXXXAY
14. ,)
3
cos(],2.5...1[,]5...1[)8.0(
2
23
X
YAXA
x
A
Y x
ÔÄĹÔÉéÔÉéÔÄęÔÄĹ
15. 2
)ln(*5,]1..5.0[*2)(cos X
A
X
AYAXAeecY x
ÔÄęÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ
16. ,)sin()2(],2.5...1[,]5.2...1[))ln(2(*
2
xXtgYAXXA
A
e
Y
x
ÔÄ≠ÔÄĹÔÉéÔÉéÔÄęÔÄĹ

17. 32
*2)
2
sin(3,]5...2[)ln(*
)ln(
**2
A
x
YAXe
x
AX
Y x
ÔÄęÔÄĹÔÄĹÔÉéÔÄĹ ÔÄ≠
18. 2
)*ln(*5,]1..5.0[*2)sin( XxAAYAXAeY x
ÔÄęÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ
19. ,)
3
2(],2.5...1[,]5...1[)(
2
X
ctgYAXXA
x
e
Y
x
ÔÄĹÔÉéÔÉéÔÄ≠ÔÄĹ
Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ](https://image.slidesharecdn.com/ocmjlvwgt1mcq1p2kvvn-signature-4a922e7935a85b02b0b80c5cfa82925cda48c81fe0e83a068d0a9d0ef03c7eba-poli-150523202516-lva1-app6891/85/429-2-mathcad-20-320.jpg)
![20. XXAAYAXAeY x
ÔÄ≠ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ ÔÄ≠
)**4ln(*5,]1..5.0[*2)cos( 2
21. ,)
4
cos(],2.5...1[,]5...1[)8.0(
*5.0
23
X
YAXA
X
X
Y x
ÔÄĹÔÉéÔÉéÔÄęÔÄĹ
22.
)cos(
4,]20...1[*25.0
2
3
X
A
YBXBY x
ÔÄĹÔÄĹÔÉéÔÄęÔÄĹ
23.
4
)2(
7,]10.0[*5*4
2
Xtg
YAX
A
X
AY ÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ
24. BxYBX
B
X
eY x
*2)2sin(4,]5.2...5.0[
*5.03
ÔÄęÔÄĹÔÄĹÔÉéÔÄ≠ÔÄĹ
25. ,)3sin(],2.5...1[,]5...1[)*2(
2
8.0 22
XYAXeA
x
Y x
x
ÔÄĹÔÉéÔÉéÔÄęÔÄĹ
26. 1.2,)
2
cos(,]5...0[)2ln(*
*2
2
5.
ÔÄĹÔÄęÔÄĹÔÉéÔÄĹ AA
x
YXx
x
x
Y
27. ]2...0[,)
3
cos(],2.5...1[,)8.0(
2
23
ÔĀįÔÉéÔÄĹÔÉéÔÄęÔÄĹ X
X
YAA
x
A
Y x
28. ]2...0[,)
3
cos(],2.5...1[,)8.0(
2
23
ÔĀįÔÉéÔÄĹÔÉéÔÄęÔÄĹ X
X
YAA
x
A
Y x
Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ](https://image.slidesharecdn.com/ocmjlvwgt1mcq1p2kvvn-signature-4a922e7935a85b02b0b80c5cfa82925cda48c81fe0e83a068d0a9d0ef03c7eba-poli-150523202516-lva1-app6891/85/429-2-mathcad-21-320.jpg)














![–°–ü–ė–°–ě–ö –õ–ė–Ę–ē–†–ź–Ę–£–†–ę
1. –ö–ł—Ä—Ć—Ź–Ĺ–ĺ–≤ –Ē.–í. Mathcad 15/Mathcad Prime 1.0. [–Ę–Ķ–ļ—Ā—ā]: –Ď–í–•-–ü–Ķ—ā–Ķ—Ä–Ī—É—Ä–≥,
2012. -428 —Ā.
1. –Ē—Ć—Ź–ļ–ĺ–Ĺ–ĺ–≤ –í.–ü. Mathcad 11/12/13 –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ: –°–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ. [–Ę–Ķ–ļ—Ā—ā]:
–ď–ĺ—Ä—Ź—á–į—Ź –Ľ–ł–Ĺ–ł—Ź-–Ę–Ķ–Ľ–Ķ–ļ–ĺ–ľ, 2007, 960 —Ā.
Copyright –ě–ź–ě ¬ę–¶–ö–Ď ¬ę–Ď–ė–Ď–ö–ě–ú¬Ľ & –ě–ě–ě ¬ęA–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ K–Ĺ–ł–≥–į-C–Ķ—Ä–≤–ł—Ā¬Ľ](https://image.slidesharecdn.com/ocmjlvwgt1mcq1p2kvvn-signature-4a922e7935a85b02b0b80c5cfa82925cda48c81fe0e83a068d0a9d0ef03c7eba-poli-150523202516-lva1-app6891/85/429-2-mathcad-37-320.jpg)
