4.3 Congruent Triangle Proofs
0 likes316 views
The document outlines the process for proving two triangles are congruent using various theorems such as AAS, HL, SAS, and ASA. It details a three-step method for setting up proof, including marking given information, identifying congruence theorems, and writing the statements and corresponding reasons. Additionally, it highlights important properties and theorems relevant to triangle congruence proofs.
1 of 10
Download to read offline








Ad
Recommended
5.3 Congruent Triangle Proofs
5.3 Congruent Triangle Proofssmiller5
╠²
This document provides guidance on writing proofs to show that two triangles are congruent. It explains that additional information is needed beyond just being given that the triangles are congruent, such as one of the congruence theorems (AAS, HL, SAS, or ASA). It then demonstrates a three step process for writing congruent triangle proofs: 1) Mark any given information; 2) Identify the congruence theorem and additional needed information; 3) Write statements with reasons, concluding what is to be proved. An example proof is given using the SSS theorem to show two triangles with two shared sides are congruent. Common theorems that can be used in proofs are also listed.5.3 Congruent Triangle Proofs & CPCTC
5.3 Congruent Triangle Proofs & CPCTCsmiller5
╠²
1. The document discusses different methods for proving triangles congruent, including using congruence theorems like SAS, SSS, ASA, and CPCTC (corresponding parts of congruent triangles are congruent).
2. It provides an example proof demonstrating the three step process: 1) mark given information, 2) identify the congruence theorem, 3) write statements and reasons.
3. Common reasons used in proofs include the reflexive property of congruence, vertical angles theorem, and parallel line theorems like corresponding angles.2.7.3 Congruent Triangle Proofs
2.7.3 Congruent Triangle Proofssmiller5
╠²
This document provides instructions for proving triangles are congruent using a two-column proof. It explains that proofs list given information, deduced information, and the statement to be proven, with reasons for each step. A basic three-step method is outlined: 1) Mark given information on the diagram, 2) Identify the congruence theorem and additional needed information, 3) Write the proof statements and reasons. An example proof is then shown demonstrating these steps, using the Side-Side-Side congruence theorem to prove two triangles with two shared sides are congruent. Common theorems that can be used in proofs are also listed.2.7.4 Congruent Triangle Proofs
2.7.4 Congruent Triangle Proofssmiller5
╠²
This document provides guidance on writing proofs to show that two triangles are congruent. It explains that a congruent triangle proof should include (1) marking given information on a diagram, (2) identifying the congruence theorem and additional information needed, and (3) writing statement reasons. An example proof is provided demonstrating these three steps, using the Side-Side-Side congruence theorem to prove triangles ABC and CBD are congruent. Common theorems that can be used in congruent triangle proofs are also listed.2.6.3 Congruent Triangle Proofs
2.6.3 Congruent Triangle Proofssmiller5
╠²
This document provides guidance on writing proofs to show that two triangles are congruent. It explains that a two-column proof lists given information, deduced information, and the statement to be proved, with reasons for each step. A basic three-step method is outlined: 1) Mark given information on the diagram, 2) Identify the congruence theorem and additional needed information, 3) Write the statements and reasons, with the last statement being what is to be proved. An example proof is provided using the Side-Side-Side congruence theorem to prove two triangles are congruent. Common theorems that can be used in proofs are also listed.Q3W6 SAS ,APRIL 2024 education S-PPT.pptx
Q3W6 SAS ,APRIL 2024 education S-PPT.pptxgoodtechpro3245
╠²
The document focuses on triangle congruence and the corresponding postulates and theorems, such as ASA, SAS, and SSS, to prove the congruence of triangles. It includes various discussions and activities to enhance understanding of key concepts, including proofs and applications of these theorems. The objectives encourage learners to illustrate, deduce, and appreciate logical reasoning related to triangle congruence.Proving Triangle Congruence Proof in mathematicss.ppt
Proving Triangle Congruence Proof in mathematicss.pptAltheaMaeGutierrez
╠²
The document outlines methods for proving the congruence of triangles, including the SAS, ASA, SSS, and AAS postulates. It also describes the importance of identifying congruent angles and sides and provides examples and practice problems for applying these concepts. Furthermore, it emphasizes the use of CPCTC (corresponding parts of congruent triangles are congruent) in proofs.10.17 Triangle Congruence Proofs Day 2.ppt
10.17 Triangle Congruence Proofs Day 2.pptMarjorie Malveda
╠²
The document discusses different methods for proving triangles congruent:
1. SSS (side-side-side)
2. SAS (side-angle-side)
3. ASA (angle-side-angle)
4. AAS (angle-angle-side)
5. HL (hypotenuse-leg) for right triangles only.
It provides examples of using these methods to determine if pairs of triangles are congruent or not. It also discusses using corresponding parts of congruent triangles (CPCTC) to prove additional parts are congruent if two triangles are already shown to be congruent.10.17 Triangle Congruence Proofs Day 2.ppt
10.17 Triangle Congruence Proofs Day 2.pptDianaJanicaMagalong2
╠²
The document discusses different methods for proving triangles congruent:
1. SSS (side-side-side)
2. SAS (side-angle-side)
3. ASA (angle-side-angle)
4. AAS (angle-angle-side)
5. HL (hypotenuse-leg) for right triangles only.
It also covers built-in information in triangles like shared sides, parallel lines, and vertical angles that can be used for proofs. The document provides examples of congruence proofs using these methods and concepts like corresponding parts of congruent triangles.10.17 Triangle Congruence Proofs Day 2.ppt
10.17 Triangle Congruence Proofs Day 2.pptmikeebio1
╠²
The document discusses different methods for proving triangles congruent:
1. SSS (side-side-side)
2. SAS (side-angle-side)
3. ASA (angle-side-angle)
4. AAS (angle-angle-side)
5. HL (hypotenuse-leg) for right triangles only.
It provides examples of using these methods to determine if pairs of triangles are congruent or not. It also discusses using corresponding parts of congruent triangles (CPCTC) to prove additional parts congruent, such as adding auxiliary lines.q4math810congruencepostulatesfortriangles-210504200358.ppt
q4math810congruencepostulatesfortriangles-210504200358.pptReifalynFulig
╠²
The document outlines the congruence postulates for triangles, which include SAS, ASA, SSS, and SAA, providing definitions and corresponding conditions for establishing triangle congruency. It includes detailed steps on how to prove triangle congruence using these postulates through various examples and methods. Each postulate connects sides and angles of triangles systematically to demonstrate their congruence.3-MATH 8-Q3-WEEK 2-ILLUSTRATING TRIANGLE CONGRUENCE AND Illustrating SSS, SAS...
3-MATH 8-Q3-WEEK 2-ILLUSTRATING TRIANGLE CONGRUENCE AND Illustrating SSS, SAS...AngelaCamillePaynant
╠²
This document provides instructions and examples for illustrating triangle congruence. It begins with an activity asking students to identify whether figure pairs are congruent or not. Next, it discusses how to pair corresponding vertices, sides, and angles of congruent triangles. Examples are given demonstrating this process. The document then discusses different postulates for triangle congruence including SSS, SAS, and ASA. It provides additional examples and activities applying these postulates. It also discusses right triangle congruence and the corresponding theorems. In all, the document aims to teach students how to determine if two triangles are congruent and explain why using appropriate triangle congruence rules and terminology.Congruence Postulates for Triangles
Congruence Postulates for TrianglesSonarin Cruz
╠²
The document discusses the different postulates for proving that two triangles are congruent: SAS, ASA, SSS, and SAA. It explains each postulate and provides examples of how to use them to prove triangles are congruent by listing corresponding parts and reasons. Steps are outlined for setting up congruence proofs, including marking givens, choosing a postulate, listing statements equal parts, and stating reasons using properties or postulates.3-math8-q3-week2-illustratingtrianglecongruenceandillustratingssssasandasa-23...
3-math8-q3-week2-illustratingtrianglecongruenceandillustratingssssasandasa-23...ReifalynFulig
╠²
The document discusses triangle congruence, explaining that congruent triangles have identical size and shape with corresponding parts that match. It outlines methods for determining triangle congruence, including SSS, SAS, ASA, AAS, and HL postulates, along with featuring examples and activities to reinforce understanding. Additionally, it emphasizes the importance of congruent triangles in real life, such as in architecture and engineering.Special Right Triangles NSpire Explore
Special Right Triangles NSpire Explorezanstett
╠²
This document describes a student activity that examines two types of special right triangles and determines the relationships between the lengths of their sides. Students are asked to drag points on interactive diagrams of an equilateral triangle and half a square to observe the ratios between the shorter leg, longer leg, and hypotenuse. They then write equations to express the relationships and confirm their observations by calculating side lengths. The activity helps students identify the 45-45-90 triangle and 30-60-90 triangle as special right triangles and define the constant ratios between their sides.Proving congruence of tw0 triangles.pptx
Proving congruence of tw0 triangles.pptxbernadethvillanueva1
╠²
The document outlines a step-by-step process for proving triangle congruence using various theorems, including SAS, SSS, AAS, and properties of angles. It provides examples demonstrating how to identify given information, choose the appropriate congruence theorem, and write proofs in a structured format. Additionally, it covers definitions relevant to triangles and congruence proofs.GCSE and IGCSE Congruent Triangles powerpoint
GCSE and IGCSE Congruent Triangles powerpointJonathanShadrachPete
╠²
Presentation from DrFrost maths on congruent triangles from the gcse specification.G8 Math Q3-Week 7- Proving Triangle Congruence.ppt
G8 Math Q3-Week 7- Proving Triangle Congruence.pptChristopherPatioCabi
╠²
The document outlines methods to prove triangle congruence, detailing shortcuts such as SSS, SAS, ASA, AAS, and HL for right triangles. It describes the reflexive property, definitions, and techniques to apply congruence postulates, along with practice problems and congruence proofs. Additionally, it introduces CPCTC, the concept that corresponding parts of congruent triangles are congruent, detailing its application in proofs.Proving-Congruent-Triangles math 8 q3.pptx
Proving-Congruent-Triangles math 8 q3.pptxRica Mae Morales Rosete
╠²
The document focuses on proving the congruence of triangles using various postulates, properties, and methods such as SAS and SSS. It outlines essential learning competencies, objectives, and includes examples and activities for practicing proofs, emphasizing the importance of diagrams and logical reasoning. It also mentions the properties of congruence including reflexive, symmetric, and transitive properties.Geometry 5-6 ASA and AAS
Geometry 5-6 ASA and AASgwilson8786
╠²
This document discusses two postulates for proving triangles congruent:
1. Angle-Side-Angle (ASA) postulate - If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
2. Angle-Angle-Side (AAS) postulate - If two angles and one non-included side of one triangle are congruent to two angles and the non-included side of another triangle, then the triangles are congruent.
The document provides examples of applying these postulates to determine if pairs of triangles are congruent. It also notes there are no AAA or SSA postulates to prove triangles congruent.Reasoning and Proof: An Introduction
Reasoning and Proof: An IntroductionSonarin Cruz
╠²
The document discusses different types of reasoning and proof in mathematics. It explains that there are two main ways to write a proof: a two-column proof and a paragraph proof. It also describes the most common steps in writing a proof, which include drawing a figure, marking deductions from given information, and writing logical statements with justifications. Examples are then provided to illustrate solving equations using direct and indirect proofs through a series of logical statements and reasons.4-4, 4-5 Congruent Triangles.ppt
4-4, 4-5 Congruent Triangles.pptsmithj91
╠²
The document discusses different methods for proving that two triangles are congruent:
- SSS (three pairs of corresponding sides are congruent)
- SAS (two pairs of corresponding sides and the included angle are congruent)
- ASA, AAS (two pairs of corresponding angles and one included or non-included side are congruent)
- HL (hypotenuse-leg theorem for right triangles, showing hypotenuse and one leg are congruent)
The document provides examples of using these methods like SAS, AAS, and ASA to prove triangles congruent through labeled diagram proofs. It emphasizes setting up the proof by marking congruent parts given and concluding that the triangles are congruent.Direct Proof and Indirect proof: Meaning and examples
Direct Proof and Indirect proof: Meaning and examplesShaymaa Mustafa
╠²
The document discusses mathematical proofs, detailing concepts such as theorems, propositions, axioms, and logical consistency. It explains proof methods including direct proof, which deduces conclusions from hypotheses, and indirect proof, which uses contradiction to establish the truth of a statement. Various examples illustrate the process of proof in both paragraph and two-column formats.7.3 proving triangles similar
7.3 proving triangles similartahirhussain665879
╠²
The document outlines the criteria for proving triangle similarity using three methods: angle-angle (AA), side-side-side (SSS), and side-angle-side (SAS). Each method is explained with corresponding conditions and examples, emphasizing that triangles are similar if their angles are congruent or sides are proportional. It also provides steps to systematically prove triangle similarity through marking given elements and selecting an appropriate method.Project in math
Project in mathraprap10
╠²
This document discusses teaching students how to write mathematical proofs through engaging activities. It provides examples of proofs involving geometry topics like congruent triangles. Students work in groups to solve proofs and then defend their arguments in a mock courtroom setting. This allows students to build confidence in supporting their logical reasoning with statements and evidence while practicing the process of writing formal proofs.Geometry
GeometryAirah Torres
╠²
This document provides information on proving triangle congruence using various postulates and properties. It discusses the six corresponding parts used to determine if two triangles are congruent, as well as five postulates for proving congruence: SSS, SAS, ASA, SAA/AAS, and the third angle theorem. Examples are given of applying each postulate, along with exercises to identify the postulate used and complete triangle congruence proofs. Key details include identifying the six corresponding parts of triangles as sides and angles, discussing the five postulates for proving congruence based on sides and angles, and providing examples of setting up triangle congruence proofs.T7.3 The Unit Circle and Angles Presentation
T7.3 The Unit Circle and Angles Presentationsmiller5
╠²
* Use the unit circle to define values for trig functions.
* Determine the measure of an angle based on the coordinates of its trig value.
T7.2 Right Triangle Trigonometry Presentation
T7.2 Right Triangle Trigonometry Presentationsmiller5
╠²
* Use right triangles to evaluate trigonometric functions
* Use equal cofunctions of complementary angles
* Use the definitions of trigonometric functions for any angle
* Use right triangle trigonometry to solve applied problemsMore Related Content
Similar to 4.3 Congruent Triangle Proofs (20)
10.17 Triangle Congruence Proofs Day 2.ppt
10.17 Triangle Congruence Proofs Day 2.pptDianaJanicaMagalong2
╠²
The document discusses different methods for proving triangles congruent:
1. SSS (side-side-side)
2. SAS (side-angle-side)
3. ASA (angle-side-angle)
4. AAS (angle-angle-side)
5. HL (hypotenuse-leg) for right triangles only.
It also covers built-in information in triangles like shared sides, parallel lines, and vertical angles that can be used for proofs. The document provides examples of congruence proofs using these methods and concepts like corresponding parts of congruent triangles.10.17 Triangle Congruence Proofs Day 2.ppt
10.17 Triangle Congruence Proofs Day 2.pptmikeebio1
╠²
The document discusses different methods for proving triangles congruent:
1. SSS (side-side-side)
2. SAS (side-angle-side)
3. ASA (angle-side-angle)
4. AAS (angle-angle-side)
5. HL (hypotenuse-leg) for right triangles only.
It provides examples of using these methods to determine if pairs of triangles are congruent or not. It also discusses using corresponding parts of congruent triangles (CPCTC) to prove additional parts congruent, such as adding auxiliary lines.q4math810congruencepostulatesfortriangles-210504200358.ppt
q4math810congruencepostulatesfortriangles-210504200358.pptReifalynFulig
╠²
The document outlines the congruence postulates for triangles, which include SAS, ASA, SSS, and SAA, providing definitions and corresponding conditions for establishing triangle congruency. It includes detailed steps on how to prove triangle congruence using these postulates through various examples and methods. Each postulate connects sides and angles of triangles systematically to demonstrate their congruence.3-MATH 8-Q3-WEEK 2-ILLUSTRATING TRIANGLE CONGRUENCE AND Illustrating SSS, SAS...
3-MATH 8-Q3-WEEK 2-ILLUSTRATING TRIANGLE CONGRUENCE AND Illustrating SSS, SAS...AngelaCamillePaynant
╠²
This document provides instructions and examples for illustrating triangle congruence. It begins with an activity asking students to identify whether figure pairs are congruent or not. Next, it discusses how to pair corresponding vertices, sides, and angles of congruent triangles. Examples are given demonstrating this process. The document then discusses different postulates for triangle congruence including SSS, SAS, and ASA. It provides additional examples and activities applying these postulates. It also discusses right triangle congruence and the corresponding theorems. In all, the document aims to teach students how to determine if two triangles are congruent and explain why using appropriate triangle congruence rules and terminology.Congruence Postulates for Triangles
Congruence Postulates for TrianglesSonarin Cruz
╠²
The document discusses the different postulates for proving that two triangles are congruent: SAS, ASA, SSS, and SAA. It explains each postulate and provides examples of how to use them to prove triangles are congruent by listing corresponding parts and reasons. Steps are outlined for setting up congruence proofs, including marking givens, choosing a postulate, listing statements equal parts, and stating reasons using properties or postulates.3-math8-q3-week2-illustratingtrianglecongruenceandillustratingssssasandasa-23...
3-math8-q3-week2-illustratingtrianglecongruenceandillustratingssssasandasa-23...ReifalynFulig
╠²
The document discusses triangle congruence, explaining that congruent triangles have identical size and shape with corresponding parts that match. It outlines methods for determining triangle congruence, including SSS, SAS, ASA, AAS, and HL postulates, along with featuring examples and activities to reinforce understanding. Additionally, it emphasizes the importance of congruent triangles in real life, such as in architecture and engineering.Special Right Triangles NSpire Explore
Special Right Triangles NSpire Explorezanstett
╠²
This document describes a student activity that examines two types of special right triangles and determines the relationships between the lengths of their sides. Students are asked to drag points on interactive diagrams of an equilateral triangle and half a square to observe the ratios between the shorter leg, longer leg, and hypotenuse. They then write equations to express the relationships and confirm their observations by calculating side lengths. The activity helps students identify the 45-45-90 triangle and 30-60-90 triangle as special right triangles and define the constant ratios between their sides.Proving congruence of tw0 triangles.pptx
Proving congruence of tw0 triangles.pptxbernadethvillanueva1
╠²
The document outlines a step-by-step process for proving triangle congruence using various theorems, including SAS, SSS, AAS, and properties of angles. It provides examples demonstrating how to identify given information, choose the appropriate congruence theorem, and write proofs in a structured format. Additionally, it covers definitions relevant to triangles and congruence proofs.GCSE and IGCSE Congruent Triangles powerpoint
GCSE and IGCSE Congruent Triangles powerpointJonathanShadrachPete
╠²
Presentation from DrFrost maths on congruent triangles from the gcse specification.G8 Math Q3-Week 7- Proving Triangle Congruence.ppt
G8 Math Q3-Week 7- Proving Triangle Congruence.pptChristopherPatioCabi
╠²
The document outlines methods to prove triangle congruence, detailing shortcuts such as SSS, SAS, ASA, AAS, and HL for right triangles. It describes the reflexive property, definitions, and techniques to apply congruence postulates, along with practice problems and congruence proofs. Additionally, it introduces CPCTC, the concept that corresponding parts of congruent triangles are congruent, detailing its application in proofs.Proving-Congruent-Triangles math 8 q3.pptx
Proving-Congruent-Triangles math 8 q3.pptxRica Mae Morales Rosete
╠²
The document focuses on proving the congruence of triangles using various postulates, properties, and methods such as SAS and SSS. It outlines essential learning competencies, objectives, and includes examples and activities for practicing proofs, emphasizing the importance of diagrams and logical reasoning. It also mentions the properties of congruence including reflexive, symmetric, and transitive properties.Geometry 5-6 ASA and AAS
Geometry 5-6 ASA and AASgwilson8786
╠²
This document discusses two postulates for proving triangles congruent:
1. Angle-Side-Angle (ASA) postulate - If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
2. Angle-Angle-Side (AAS) postulate - If two angles and one non-included side of one triangle are congruent to two angles and the non-included side of another triangle, then the triangles are congruent.
The document provides examples of applying these postulates to determine if pairs of triangles are congruent. It also notes there are no AAA or SSA postulates to prove triangles congruent.Reasoning and Proof: An Introduction
Reasoning and Proof: An IntroductionSonarin Cruz
╠²
The document discusses different types of reasoning and proof in mathematics. It explains that there are two main ways to write a proof: a two-column proof and a paragraph proof. It also describes the most common steps in writing a proof, which include drawing a figure, marking deductions from given information, and writing logical statements with justifications. Examples are then provided to illustrate solving equations using direct and indirect proofs through a series of logical statements and reasons.4-4, 4-5 Congruent Triangles.ppt
4-4, 4-5 Congruent Triangles.pptsmithj91
╠²
The document discusses different methods for proving that two triangles are congruent:
- SSS (three pairs of corresponding sides are congruent)
- SAS (two pairs of corresponding sides and the included angle are congruent)
- ASA, AAS (two pairs of corresponding angles and one included or non-included side are congruent)
- HL (hypotenuse-leg theorem for right triangles, showing hypotenuse and one leg are congruent)
The document provides examples of using these methods like SAS, AAS, and ASA to prove triangles congruent through labeled diagram proofs. It emphasizes setting up the proof by marking congruent parts given and concluding that the triangles are congruent.Direct Proof and Indirect proof: Meaning and examples
Direct Proof and Indirect proof: Meaning and examplesShaymaa Mustafa
╠²
The document discusses mathematical proofs, detailing concepts such as theorems, propositions, axioms, and logical consistency. It explains proof methods including direct proof, which deduces conclusions from hypotheses, and indirect proof, which uses contradiction to establish the truth of a statement. Various examples illustrate the process of proof in both paragraph and two-column formats.7.3 proving triangles similar
7.3 proving triangles similartahirhussain665879
╠²
The document outlines the criteria for proving triangle similarity using three methods: angle-angle (AA), side-side-side (SSS), and side-angle-side (SAS). Each method is explained with corresponding conditions and examples, emphasizing that triangles are similar if their angles are congruent or sides are proportional. It also provides steps to systematically prove triangle similarity through marking given elements and selecting an appropriate method.Project in math
Project in mathraprap10
╠²
This document discusses teaching students how to write mathematical proofs through engaging activities. It provides examples of proofs involving geometry topics like congruent triangles. Students work in groups to solve proofs and then defend their arguments in a mock courtroom setting. This allows students to build confidence in supporting their logical reasoning with statements and evidence while practicing the process of writing formal proofs.Geometry
GeometryAirah Torres
╠²
This document provides information on proving triangle congruence using various postulates and properties. It discusses the six corresponding parts used to determine if two triangles are congruent, as well as five postulates for proving congruence: SSS, SAS, ASA, SAA/AAS, and the third angle theorem. Examples are given of applying each postulate, along with exercises to identify the postulate used and complete triangle congruence proofs. Key details include identifying the six corresponding parts of triangles as sides and angles, discussing the five postulates for proving congruence based on sides and angles, and providing examples of setting up triangle congruence proofs.3-MATH 8-Q3-WEEK 2-ILLUSTRATING TRIANGLE CONGRUENCE AND Illustrating SSS, SAS...
3-MATH 8-Q3-WEEK 2-ILLUSTRATING TRIANGLE CONGRUENCE AND Illustrating SSS, SAS...AngelaCamillePaynant
╠²
More from smiller5 (20)
T7.3 The Unit Circle and Angles Presentation
T7.3 The Unit Circle and Angles Presentationsmiller5
╠²
* Use the unit circle to define values for trig functions.
* Determine the measure of an angle based on the coordinates of its trig value.
T7.2 Right Triangle Trigonometry Presentation
T7.2 Right Triangle Trigonometry Presentationsmiller5
╠²
* Use right triangles to evaluate trigonometric functions
* Use equal cofunctions of complementary angles
* Use the definitions of trigonometric functions for any angle
* Use right triangle trigonometry to solve applied problems1.3 Factoring Quadratics (Presentation).pdf
1.3 Factoring Quadratics (Presentation).pdfsmiller5
╠²
Review factoring polynomial and quadratic expressions.1.3 Factoring Polynomial and Quadratic Expressions
1.3 Factoring Polynomial and Quadratic Expressionssmiller5
╠²
Review factoring polynomial and quadratic expressions.Trigonometry 7.1 Angles (Degrees and Radians)
Trigonometry 7.1 Angles (Degrees and Radians)smiller5
╠²
* Convert between degrees and radians
* Find coterminal angles
* Find the length of a circular arc
* Find the area of a sector
6.7 Exponential and Logarithmic Models
6.7 Exponential and Logarithmic Modelssmiller5
╠²
Chapter 6 covers exponential and logarithmic functions, focusing on modeling exponential growth and decay, NewtonÔÇÖs law of cooling, and logistic growth models. It provides formulas for representing these phenomena mathematically, with examples illustrating population dynamics and applications such as carbon-14 dating. Key concepts include the general equations for exponential growth and decay, half-life, and the transition to base e logarithms.4.5 Special Segments in Triangles
4.5 Special Segments in Trianglessmiller5
╠²
The document covers essential concepts related to special segments in triangles, including perpendicular and angle bisectors, as well as key centers like circumcenter, incenter, centroid, and orthocenter. It discusses theorems related to these segments, such as the perpendicular bisector and angle bisector theorems, and provides examples for problem-solving. Various triangle constructions and their properties are also highlighted to aid understanding.1.4 Conditional Statements
1.4 Conditional Statementssmiller5
╠²
The document covers conditional statements, including how to identify, write, and analyze them, as well as the concepts of converses, inverses, contrapositive, and counterexamples. It explains inductive reasoning and provides examples of conjectures with counterexamples that demonstrate their validity. Additionally, it introduces biconditional statements and outlines the steps to write conditional statements, converses, inverses, and biconditionals.1.3 Distance and Midpoint Formulas
1.3 Distance and Midpoint Formulassmiller5
╠²
The document outlines the distance and midpoint formulas for finding distances and midpoints between given points on a coordinate plane. It provides examples, problems, and explanations on how to calculate endpoints and points a fractional distance from one end of a segment. The document aims to equip students with the ability to apply these formulas effectively.1.5 Quadratic Equations.pdf
1.5 Quadratic Equations.pdfsmiller5
╠²
This document provides instruction on factoring polynomials and quadratic equations. It begins by reviewing factoring techniques like finding the greatest common factor and factoring trinomials and binomials. Examples are provided to demonstrate the factoring methods. The document then discusses solving quadratic equations by factoring, putting the equation in standard form, and setting each factor equal to zero. An example problem demonstrates solving a quadratic equation through factoring. The document concludes by assigning homework and an optional reading for the next class.3.2 Graphs of Functions
3.2 Graphs of Functionssmiller5
╠²
This document covers the concepts of functions and their graphs, focusing on piecewise-defined functions, absolute value functions, and greatest-integer functions. It provides examples illustrating how to graph these functions and interpret their results, emphasizing the importance of the vertical line test to determine whether a relation is a function. Additionally, real-world applications such as water billing based on usage and graphing sales prices of houses are presented to demonstrate these mathematical concepts.3.2 Graphs of Functions
3.2 Graphs of Functionssmiller5
╠²
The document covers concepts related to graphs of functions, including piecewise-defined, absolute value, and greatest-integer functions. It explains how to graph these functions, the importance of interpreting graphs in real-world contexts, and provides examples related to water usage billing and mailing costs. Additionally, the document emphasizes the vertical line test for determining if a relation is a function.3.1 Functions
3.1 Functionssmiller5
╠²
The document outlines the concepts of functions, including function notation, domain, and range, as part of a Business College Algebra course. It illustrates the definition of functions with examples, such as the relationship between time and distance for a falling rock, and discusses the use of piecewise-defined functions through practical examples like state income tax calculations. The section concludes with assignments to reinforce the learned material.2.5 Transformations of Functions
2.5 Transformations of Functionssmiller5
╠²
This document discusses transformations of functions, focusing on techniques for recognizing and graphing common functions through vertical and horizontal shifts, reflections, compressions, and stretches. It introduces 'toolkit functions' as essential building blocks for understanding graph behavior and outlines their properties and transformations. The document also summarizes how to combine these transformations and prepares users for further practice in subsequent lessons.2.2 More on Functions and Their Graphs
2.2 More on Functions and Their Graphssmiller5
╠²
This document discusses functions and their graphs. It defines increasing, decreasing and constant functions based on how the function values change as the input increases. Relative maxima and minima are points where a function changes from increasing to decreasing. Symmetry of functions is classified by the y-axis, x-axis and origin. Even functions are symmetric about the y-axis, odd functions are symmetric about the origin. Piecewise functions have different definitions over different intervals.1.6 Other Types of Equations
1.6 Other Types of Equationssmiller5
╠²
This document provides examples and steps for solving various types of equations beyond linear equations, including:
1) Polynomial equations solved by factoring
2) Equations with radicals where radicals are eliminated by raising both sides to a power
3) Equations with rational exponents where both sides are raised to the reciprocal power
4) Equations quadratic in form where an algebraic substitution is made to transform into a quadratic equation
5) Absolute value equations where both positive and negative solutions must be considered.1.5 Quadratic Equations (Review)
1.5 Quadratic Equations (Review)smiller5
╠²
This document provides instruction on factoring quadratic equations. It begins by reviewing factoring polynomials and trinomials. It then discusses factoring binomials using difference of squares, sum/difference of cubes, and other patterns. Finally, it explains that a quadratic equation can be solved by factoring if it can be written as a product of two linear factors. An example demonstrates factoring a quadratic equation by finding the two values that make each factor equal to zero.2.1 Basics of Functions and Their Graphs
2.1 Basics of Functions and Their Graphssmiller5
╠²
This document provides an overview of functions and their graphs. It defines what constitutes a function, discusses domain and range, and how to identify functions using the vertical line test. Key points covered include:
- A function is a relation where each input has a single, unique output
- The domain is the set of inputs and the range is the set of outputs
- Functions can be represented by ordered pairs, graphs, or equations
- The vertical line test identifies functions as those where a vertical line intersects the graph at most once
- Intercepts occur where the graph crosses the x or y-axis9.6 Binomial Theorem
9.6 Binomial Theoremsmiller5
╠²
The document discusses the binomial theorem, which provides a formula for expanding binomial expressions of the form (a + b)^n. It gives the formula for finding the coefficient of the term containing b^r as nCr. Several examples are worked out applying the binomial theorem to expand binomial expressions and find specific terms. Factorial notation is introduced for writing the coefficients. The document also discusses using calculators and Desmos to evaluate binomial coefficients. Practice problems are assigned from previous sections.13.3 Venn Diagrams & Two-Way Tables
13.3 Venn Diagrams & Two-Way Tablessmiller5
╠²
The document discusses using Venn diagrams and two-way tables to organize data and calculate probabilities. It provides examples of completing Venn diagrams and two-way tables based on survey data about students' activities. It then uses the tables and diagrams to calculate probabilities of different outcomes. The examples illustrate how to set up and use these visual representations of categorical data.Ad
Recently uploaded (20)
THE PSYCHOANALYTIC OF THE BLACK CAT BY EDGAR ALLAN POE (1).pdf
THE PSYCHOANALYTIC OF THE BLACK CAT BY EDGAR ALLAN POE (1).pdfnabilahk908
╠²
Psychoanalytic Analysis of The Black Cat by Edgar Allan Poe explores the deep psychological dimensions of the narratorÔÇÖs disturbed mind through the lens of Sigmund FreudÔÇÖs psychoanalytic theory. According to Freud (1923), the human psyche is structured into three components: the Id, which contains primitive and unconscious desires; the Ego, which operates on the reality principle and mediates between the Id and the external world; and the Superego, which reflects internalized moral standards.
In this story, Poe presents a narrator who experiences a psychological breakdown triggered by repressed guilt, aggression, and internal conflict. This analysis focuses not only on the gothic horror elements of the narrative but also on the narratorÔÇÖs mental instability and emotional repression, demonstrating how the imbalance of these three psychic forces contributes to his downfall.CRYPTO TRADING COURSE BY FINANCEWORLD.IO
CRYPTO TRADING COURSE BY FINANCEWORLD.IOAndrewBorisenko3
╠²
Unlock the Secrets of Crypto Trading with FinanceWorld.io!
Are you ready to dive into the exciting world of cryptocurrency trading? This comprehensive course by FinanceWorld.io is designed for beginners and intermediate traders who want to master the fundamentals of crypto markets, technical analysis, risk management, and trading strategies.
What youÔÇÖll learn:
Introduction to blockchain and cryptocurrencies
How crypto markets work
Setting up wallets and trading accounts securely
Understanding exchanges and order types
Reading charts and technical analysis basics
Essential indicators and market signals
Risk management and portfolio diversification
Real-life trading strategies and case studies
Common mistakes and how to avoid them
Who should view this course?
Aspiring crypto traders
Investors seeking additional income sources
Anyone curious about the future of decentralized finance
Why FinanceWorld.io?
Our experts make complex concepts simple, helping you gain the confidence to navigate volatile markets and capitalize on opportunities.
Ready to start your crypto journey?
View this slide deck now and take your first step towards becoming a successful crypto trader with FinanceWorld.io!Public Health For The 21st Century 1st Edition Judy Orme Jane Powell
Public Health For The 21st Century 1st Edition Judy Orme Jane Powelltrjnesjnqg7801
╠²
Public Health For The 21st Century 1st Edition Judy Orme Jane Powell
Public Health For The 21st Century 1st Edition Judy Orme Jane Powell
Public Health For The 21st Century 1st Edition Judy Orme Jane PowellHistoPathology Ppt. Arshita Gupta for Diploma
HistoPathology Ppt. Arshita Gupta for Diplomaarshitagupta674
╠²
Hello everyone please suggest your views and likes so that I uploaded more study materials
In this slide full HistoPathology according to diploma course available like fixation
Tissue processing , staining etc
2025 June Year 9 Presentation: Subject selection.pptx
2025 June Year 9 Presentation: Subject selection.pptxmansk2
╠²
2025 June Year 9 Presentation: Subject selectionOBSESSIVE COMPULSIVE DISORDER.pptx IN 5TH SEMESTER B.SC NURSING, 2ND YEAR GNM...
OBSESSIVE COMPULSIVE DISORDER.pptx IN 5TH SEMESTER B.SC NURSING, 2ND YEAR GNM...parmarjuli1412
╠²
OBSESSIVE COMPULSIVE DISORDER INCLUDED TOPICS ARE INTRODUCTION, DEFINITION OF OBSESSION, DEFINITION OF COMPULSION, MEANING OF OBSESSION AND COMPULSION, DEFINITION OF OBSESSIVE COMPULSIVE DISORDER, EPIDERMIOLOGY OF OCD, ETIOLOGICAL FACTORS OF OCD, CLINICAL SIGN AND SYMPTOMS OF OBSESSION AND COMPULSION, MANAGEMENT INCLUDED PHARMACOTHERAPY(ANTIDEPRESSANT DRUG+ANXIOLYTIC DRUGS), PSYCHOTHERAPY, NURSING MANAGEMENT(ASSESSMENT+DIAGNOSIS+NURSING INTERVENTION+EVALUATION)) Peer Teaching Observations During School Internship
Peer Teaching Observations During School InternshipAjayaMohanty7
╠²
FOR B.ED,M.ED,M.A.EDUCATION AND ANY STUDENT OF TEACHER EDUCATIONHow to use search fetch method in Odoo 18
How to use search fetch method in Odoo 18Celine George
╠²
The search_fetch is a powerful ORM method used in Odoo for some specific addons to combine the functionality of search and read for more efficient data fetching. It might be used to search for records and fetch specific fields in a single call. It stores the result in the cache memory.How to Add New Item in CogMenu in Odoo 18
How to Add New Item in CogMenu in Odoo 18Celine George
╠²
In Odoo 18, CogMenu (or Configuration Menu) is a feature typically found in various modules that allows users to configure settings related to that specific module. It has a cogwheel like icon usually located on the top left side of the screen. By default, the features for Importing and Exporting will be available inside the menu.Photo chemistry Power Point Presentation
Photo chemistry Power Point Presentationmprpgcwa2024
╠²
Photochemistry is the branch of chemistry that deals with the study of chemical reactions and processes initiated by light.
Photochemistry involves the interaction of light with molecules, leading to electronic excitation. Energy from light is transferred to molecules, initiating chemical reactions.
Photochemistry is used in solar cells to convert light into electrical energy.
It is used Light-driven chemical reactions for environmental remediation and synthesis. Photocatalysis helps in pollution abatement and environmental cleanup. Photodynamic therapy offers a targeted approach to treating diseases It is used in Light-activated treatment for cancer and other diseases.
Photochemistry is used to synthesize complex organic molecules.
Photochemistry contributes to the development of sustainable energy solutions.LDMMIA Shop & Student News Summer Solstice 25
LDMMIA Shop & Student News Summer Solstice 25LDM & Mia eStudios
╠²
6/18/25
Shop, Upcoming: Final Notes to Review as we Close Level One. Make sure to review the orientation and videos as well. ThereÔÇÖs more to come and material to cover in Levels 2-3. The content will be a combination of Reiki and Yoga. Also energy topics of our spiritual collective.
Thanks again all future Practitioner Level Students. Our Levels so far are: Guest, Grad, and Practitioner. We have had over 5k Spring Views.
https://ldm-mia.creator-spring.comHow to use _name_search() method in Odoo 18
How to use _name_search() method in Odoo 18Celine George
╠²
In Odoo, the _name_search() method is used to implement or extend the logic for searching records by name or other fields. It is typically invoked when a user types into a many-to-one or many-to-many field's search box in the user interface. Tanja Vujicic - PISA for Schools contact Info
Tanja Vujicic - PISA for Schools contact InfoEduSkills OECD
╠²
Tanja Vujicic, Senior Analyst and PISA for SchoolÔÇÖs Project Manager at the OECD spoke at the OECD webinar 'Turning insights into impact: What do early case studies reveal about the power of PISA for Schools?' on 20 June 2025
PISA for Schools is an OECD assessment that evaluates 15-year-old performance on reading, mathematics, and science. It also gathers insights into studentsÔÇÖ learning environment, engagement and well-being, offering schools valuable data that help them benchmark performance internationally and improve education outcomes. A central ambition, and ongoing challenge, has been translating these insights into meaningful actions that drives lasting school improvement. How payment terms are configured in Odoo 18
How payment terms are configured in Odoo 18Celine George
╠²
Payment terms in Odoo 18 help define the conditions for when invoices are due. This feature can split payments into multiple parts and automate due dates based on specific rules.M&A5 Q1 1 differentiate evolving early Philippine conventional and contempora...
M&A5 Q1 1 differentiate evolving early Philippine conventional and contempora...ErlizaRosete
╠²
MAPEH 6 QI WEEK IGreat Governors' Send-Off Quiz 2025 Prelims IIT KGP
Great Governors' Send-Off Quiz 2025 Prelims IIT KGPIIT Kharagpur Quiz Club
╠²
Prelims of the Great Governors' Send-Off Quiz 2025 hosted by the outgoing governors.
QMs: Aarushi, Aatir, Aditya, ArnavAd
4.3 Congruent Triangle Proofs
- 1. Congruent Triangle Proofs The student is able to (I can): ÔÇó Determine what additional information is needed to prove two triangles congruent by a given theorem ÔÇó Create two-column proofs to show that two triangles are congruent
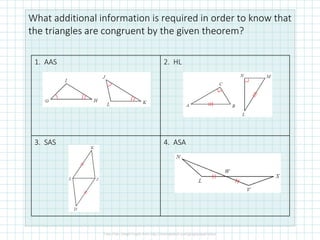
- 2. What additional information is required in order to know that the triangles are congruent by the given theorem? 1. AAS 2. HL 3. SAS 4. ASA
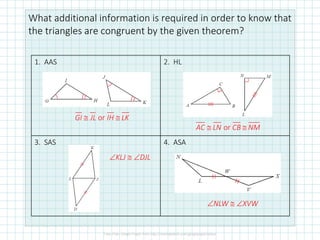
- 3. What additional information is required in order to know that the triangles are congruent by the given theorem? 1. AAS 2. HL 3. SAS 4. ASA or GI JL IH LK ´üÇ ´üÇ or AC LN CB NM ´üÇ ´üÇ ´âÉKLJ ´üÇ ´âÉDJL ´âÉNLW ´üÇ ´âÉXVW
- 4. When you are creating a proof, you list the information that you are given, list any other information you can deduce, and then whatever it is you are trying to prove. It is equally important that you give reasons for each step that you list, whether you are listing given information or information you have deduced using theorems and postulates. While congruent triangle proofs can be a little challenging, I have a basic three-step method that I use to set them up.
- 5. Three Steps to a Proof Step 1: Mark the given information on the diagram and any other information you know such as vertical angles, a shared side, or angles formed by parallel lines. Step 2: Identify the congruence theorem to be used and the additional information needed and why. Step 3: Write down the statements and the reasons. Make sure your last statement is what you are supposed to be proving.
- 6. Example Given: Prove: ╬öABD ´üÇ ╬öCBD Step 1: Based on the given information, mark the congruent sides with matching pairs of tick marks. ´üÇ ´üÇ and AB BC AD CD A B C D
- 7. Example Given: Prove: ╬öABD ´üÇ ╬öCBD Step 1: Based on the given information, mark the congruent sides with matching pairs of tick marks. Step 2: We have two sides congruent, so we will either use SSS or SAS. (Remember, SSA is not valid!) We have a shared side (and no angle indications), so we will use SSS. and AB BC AD CD ´üÇ ´üÇ A B C D
- 8. Example Given: Prove: ╬öABD ´üÇ ╬öCBD Step 1: Based on the given information, mark the congruent sides with matching pairs of tick marks. Step 2: We have two sides congruent, so we will either use SSS or SAS. (Remember, SSA is not valid!) We have a shared side (and no angle indications), so we will use SSS. Step 3: Write the proof, with one statement and reason for each side, and the final statement is what we are proving. and AB BC AD CD ´üÇ ´üÇ A B C D
- 9. Example Given: Prove: ╬öABD ´üÇ ╬öCBD Step 3: and AB BC AD CD ´üÇ ´üÇ A B C D Statements Reasons S 1. 1. Given S 2. 2. Given S 3. 3. Refl. prop. ´üÇ 4. ╬öABD ´üÇ ╬öCBD 4. SSS AB BC ´üÇ AD CD ´üÇ BD BD ´üÇ
- 10. Remember, any definition, theorem, or postulate we have worked with this year is fair game on a proof, but here are the most common ones we will use: ÔÇó Reflexive property of congruence (Refl. prop. ´üÇ) (Use on shared sides or shared angles) ÔÇó Vertical angles theorem (Vert. ´âÉs ´üÇ) ÔÇó Midpoint theorem (Midpt. thm) ÔÇó Segment and/or angle bisectors ÔÇó Any of the parallel line theorems ÔÇô Corresponding angles (Corr. ´âÉs ´üÇ) ÔÇô Alternate interior angles (Alt. int. ´âÉs ´üÇ) ÔÇô Alternate exterior angles (Alt.ext. ´âÉs ´üÇ)